內孤立波數值造波方法及其與理論和實驗結果的比較*

李效民　張　林　郭海燕　姜　海　王　偉

(中國海洋大學工程學院　青島　266100)

經過長期的開采,陸上油氣資源日益減少,人們把目光轉向了資源豐富的海洋; 而復雜的海洋環境存在許多制約海洋開發的因素,內波即是其中之一。內波會對海洋立管、海洋平臺等海洋結構物產生較強的破壞作用,給海洋油氣的開發帶來極大的挑戰。

海洋內波是發生在密度穩定層化的海水內部的一種波動。海洋內波的頻率和波速遠小于表面波,但波長和振幅遠大于表面波。據記載,最大垂向振幅高達180m(方欣華等,2005)。內孤立波是一種強非線性潮成內波,主要通過非線性效應與色散效應達到一定程度的平衡,實現穩定傳播(Osborneet al,1980)。

目前廣泛使用的內孤立波理論模型有 KdV理論、eKdV理論、mKdV理論、MCC理論等。研究內孤立波的手段有理論分析、實地觀測及實測圖像分析、物理實驗、數值模擬,其中,物理實驗和數值模擬實施簡便、結果直觀可靠、適用性較強,深受研究者的青睞,而數值模擬更是憑借其成本低、可重復性好、快速的優勢成為最常用的內孤立波研究方法。Wei等(2009)采用質量源數值造波方法模擬了兩層流體中內孤立波的生成與傳播。付東明等(2009)結合KdV和mKdV理論發展了雙推板數值造波方法。陳鈺等(2009)利用 Fluent軟件,采用速度入射邊界法,成功建立了模擬弱非線性內孤立波的分層數值水槽。王旭等(2014)結合內孤立波理論進一步研究了質量源數值造波方法,與理論結果較符合。Zhang等(2012)使用 CFD方法建立了三維數值水槽,所得結果與KdV理論結果吻合較好。高原雪等(2012)基于 MCC理論,采用速度入射邊界法建立數值水槽,實現了振幅可控的內孤立波數值模擬。目前國內外主要將數值模擬結果與理論結果進行對比分析,而將理論、實驗、數值模擬三者進行對比分析的研究較少。此外,對各種數值造波方法優劣的比較也較為缺乏。

本文針對三種內孤立波理論模型與數值造波方法,基于KdV、mKdV和eKdV三種理論模型與雙推板、平板拍擊和速度入射邊界三種數值造波方法所組成的一系列工況,利用Fluent軟件進行計算,并將數值模擬結果與理論公式及實驗結果進行對比分析,驗證了數值造波的合理性,評估了這三種數值造波方法。

1　內孤立波理論模型

采用有限水深兩層流體簡化模型,假設上下層流體為無旋且不可壓縮的理想流體,上層流體密度為ρ1,深度為h1,下層流體密度為ρ2,深度為h2,總水深為h=h1+h2。如圖1,建立直角坐標系oxyz。其中oxy平面為未擾動的兩層流體界面,ox軸正向為內孤立波傳播方向,oz軸垂直于oxy面向上。令η(x,t)表示內孤立波的波面函數;為振幅大小,符號滿足上凸波為正,下凹波為負;λ為內孤立波特征波長;c為內孤立波相速度。

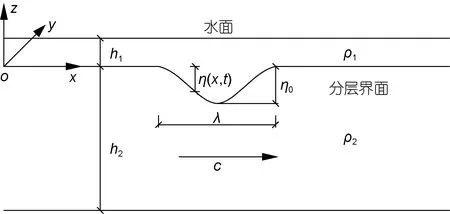
圖1　內孤立波及其參數Fig.1　Schema of internal solitary wave and the parameterization

1.1　KdV理論

波面方程的KdV理論解為(Choiet al,1999):

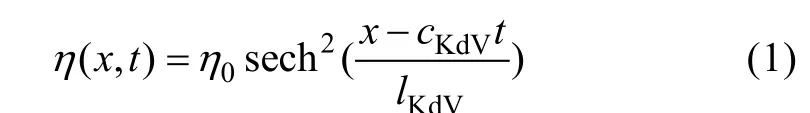
其中:

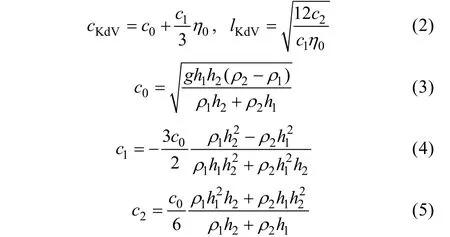
式中cKdV為 KdV理論下內孤立波的相速度;lKdV為KdV理論下內孤立波的特征長度。

KdV理論不存在極限振幅。但實驗研究發現,振幅與水深比小于0.1時,KdV理論完全適用,而對于大振幅內孤立波不再適用。

1.2　eKdV理論

波面方程的eKdV理論解為(Helfrichet al,2006):

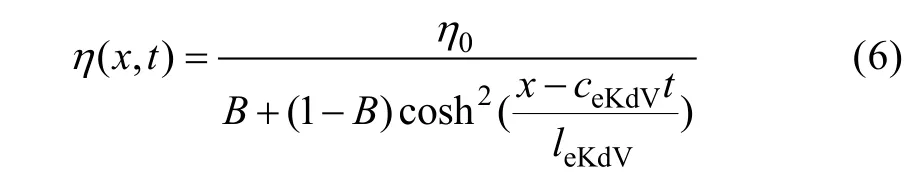
其中:

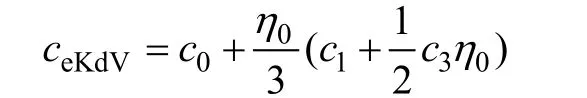
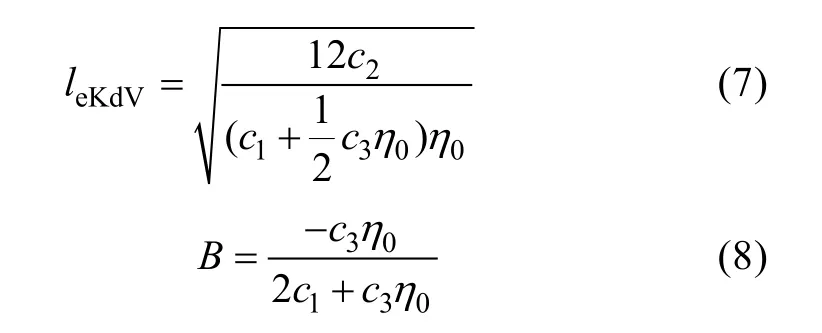
式中ceKdV為eKdV理論下內孤立波的相速度。

eKdV理論適用于振幅與水深比超過0.1的廣泛振幅范圍,且存在極限振幅,其大小為:

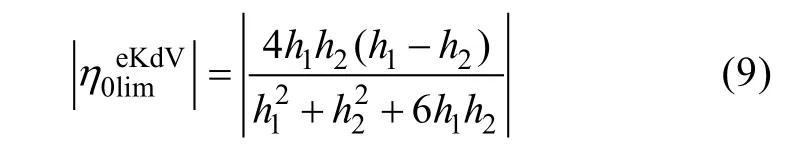
1.3　mKdV理論

波面方程的 mKdV理論解為(Michalletet al,1998):

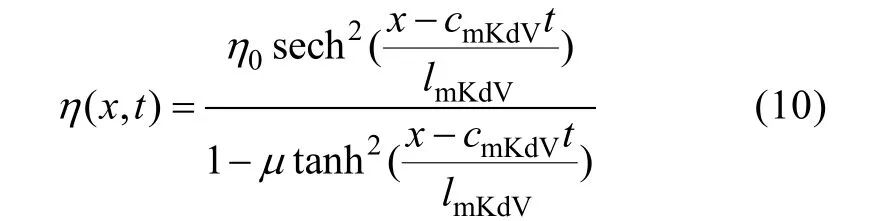
其中:

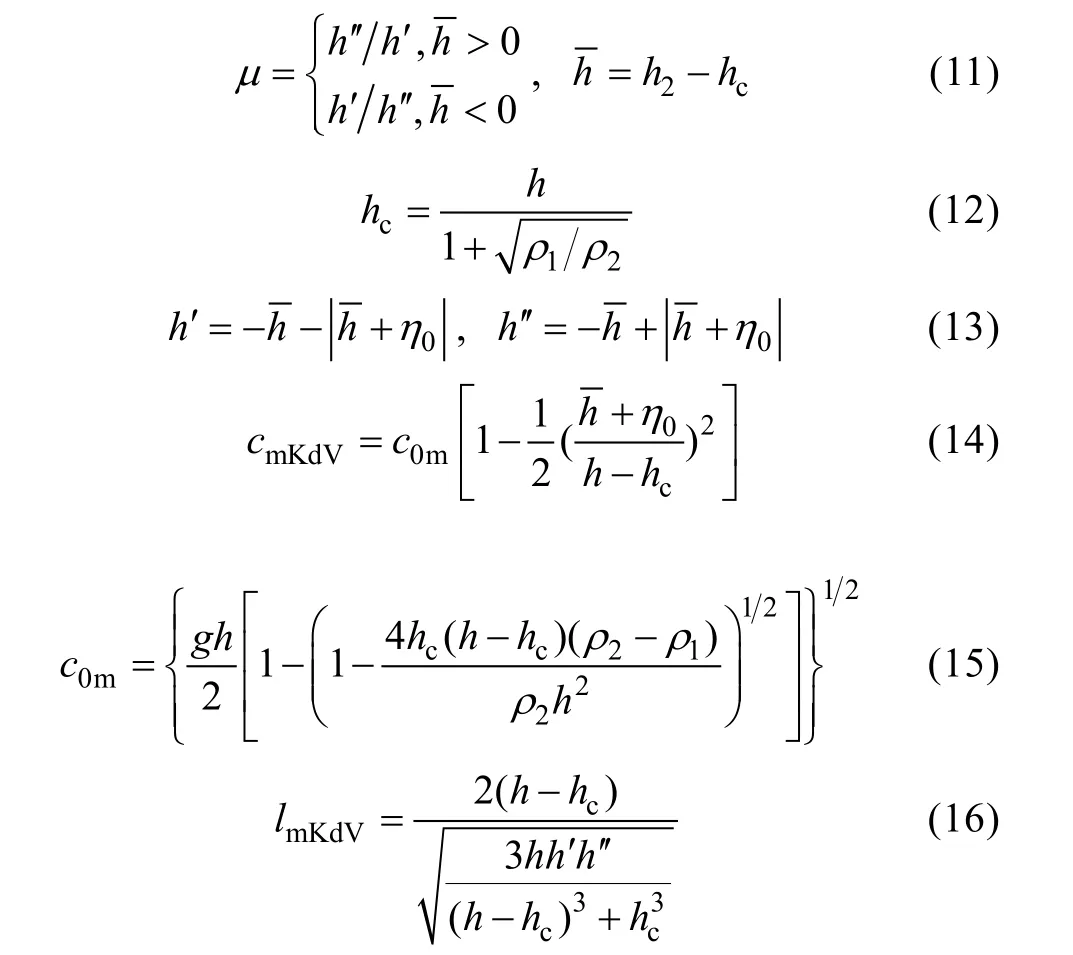
式中cmKdV為mKdV理論下內孤立波的相速度;為極限振幅大小。

mKdV理論適用于振幅與水深比超過0.1且上下層水深比接近臨界水深比的情況。

2　數值造波方法

目前,數值造波方法可大致歸為兩類: 一類是仿物理造波法,該方法源于實驗室造波技術,即仿造物理造波機的工作原理。如: 推板法、平板拍擊法等。另一類是純數值造波法,如: 速度入射邊界法等。

2.1　雙推板法

圖2為雙推板法的示意圖,水槽上、下邊界及右邊界設置為固壁邊界,左側上、下推板設置為移動邊界。其造波原理為: 選取合適的內孤立波理論,采用動網格技術,通過用戶自定義函數(UDF)的DEFINE_CG_MOTION宏控制兩塊推板的水平反向運動實現兩層流體界面處內孤立波的模擬。

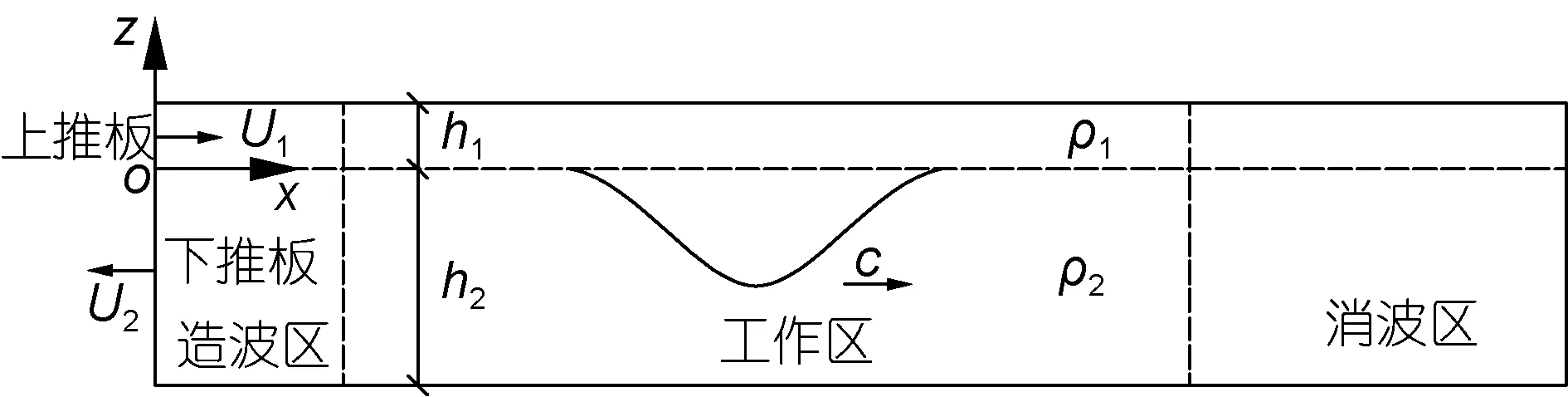
圖2　雙推板法造波示意圖Fig.2　Wave generation by double push-pedals method

令上板高度為d1,下板高度為d2,上下板的水平運動速度分別為:U1、U2。根據上推板運動排開的流體體積與兩層流體界面處水位在水平方向的積分相等,即:

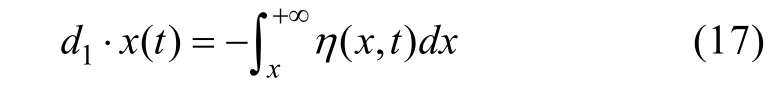
可得上推板運動速度為(徐鑫哲,2012):

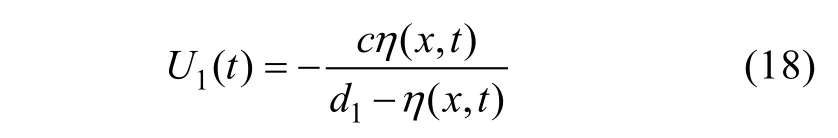
再根據流體質量守恒(徐鑫哲,2012),得下推板運動速度為:

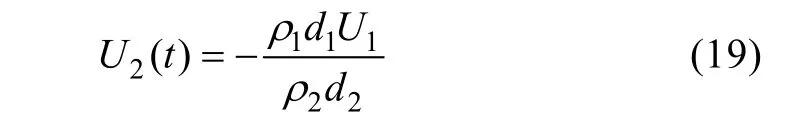
式中c為內孤立波的相速度,η(x,t)為內孤立波波面函數(上凸波為正,下凹波為負)。

實際設置時,應使d1略大于以防上下層流體摻混(付東明等,2009)。

2.2　平板拍擊法

圖3為平板拍擊法的示意圖,水槽上、下、左、右邊界及隔板均設置為固壁邊界,造波板設置為移動邊界。其造波原理為: 選取合適的內孤立波理論,采用動網格技術,通過用戶自定義函數(UDF)的DEFINE_CG_MOTION宏控制造波板做上下運動實現兩層流體界面處內孤立波的模擬。

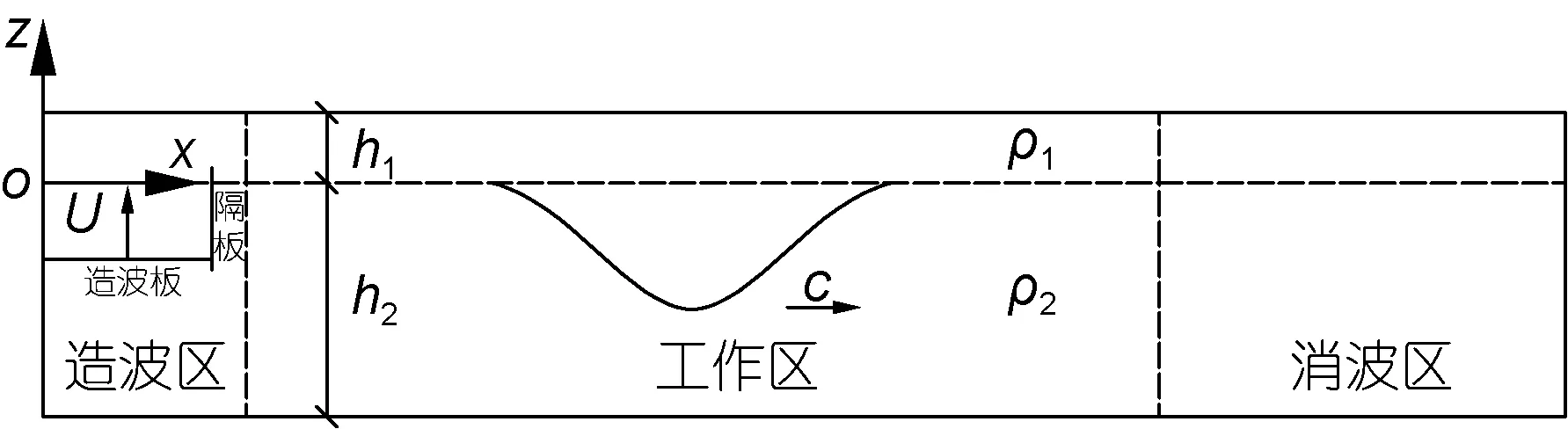
圖3　平板拍擊法造波示意圖Fig.3　Wave generation by moving pedal method

令造波板的長度為D,運動速度為U。根據造波板移動所排開的流體體積與造波板右端兩層流體界面處水位在水平方向的積分相等,即:

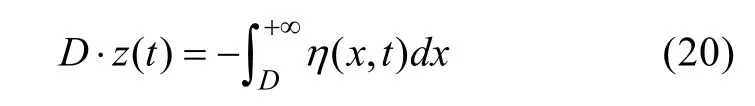
可得造波板運動速度為(徐鑫哲,2012):

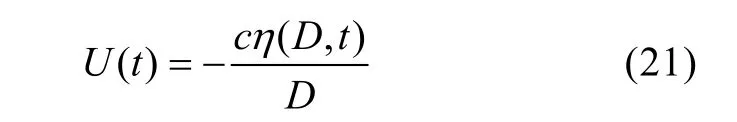
2.3　速度入射邊界法

圖4為速度入射邊界法的造波示意圖,水槽上、下邊界及右邊界設置為固壁邊界,左側邊界設置為速度入射邊界。該方法是以邊界為擾動源,但邊界是固定不運動的。其造波原理為: 選取合適的內孤立波理論,通過用戶自定義函數(UDF)的 DEFINE_PROFILE宏在入射邊界上給定該理論下的水流速度實現兩層流體界面處內孤立波的模擬。

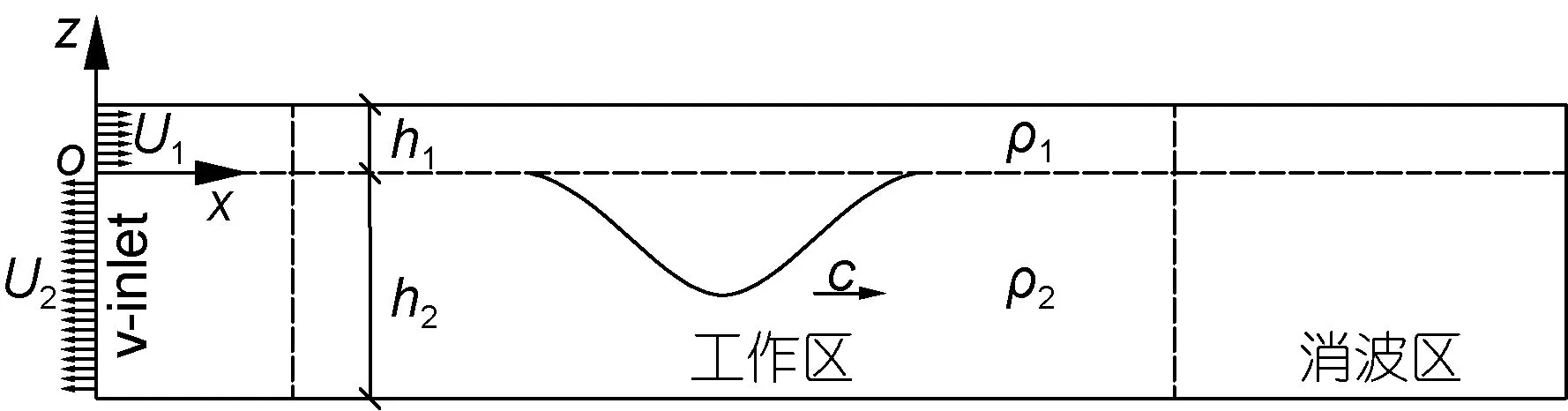
圖4　速度入射邊界法造波示意圖Fig.4　Wave generation by velocity-inlet boundary method

入射邊界處水流速度設為:

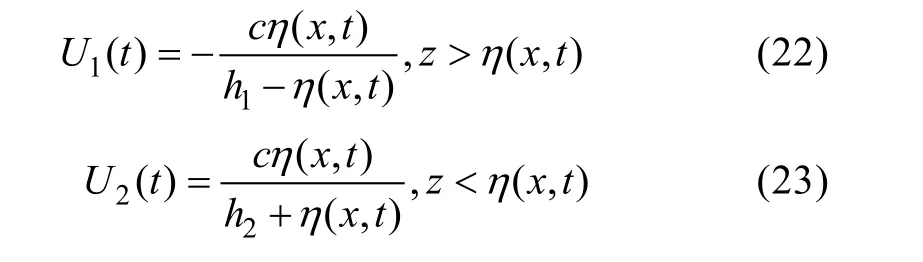
3　數值模擬與結果分析

3.1　內孤立波物理實驗

王飛(2015)在中國海洋大學物理海洋實驗室分層流體水槽中進行了內孤立波物理實驗。水槽長15m,寬0.35m,高0.7m,額定水深0.6m。采用Oster雙缸法制取密度分層流體,上層流體高度 9.5cm,密度1035kg/m3,下層流體高度48.5cm,密度1054kg/m3。采用重力塌陷法制造不同振幅的內孤立波,使用兩個斜面在水槽末端進行消波,利用PIV技術對內孤立波致流場進行測量,使用高速相機進行圖像采集,利用圖像處理軟件進行數據分析。物理實驗結果如圖6、圖8所示。

3.2　建立數值水槽

為便于與實驗結果對比,本文參照內波實驗建立數值水槽模型。采用兩層流體簡化模型,利用Fluent進行內孤立波數值模擬。采用結構化網格離散,在兩層流體交界面附近對網格劃分進行加密。工作區網格劃分如圖5(a)所示: 底部向上38cm至50cm高度范圍內,網格尺寸為0.5cm,其余為1cm,x軸方向網格尺寸為2cm。選用二維不可壓縮Navier-Stokes方程作為流體控制方程,使用有限體積法對控制方程進行離散。選用κ-ε湍流模型,采用VOF方法追蹤兩層流體的交界面,兩層流體界面的構造采用幾何重構法,壓力速度耦合選用 PISO算法,壓力插值采用體積力加權法,對流相及輸運方程的離散采用一階迎風格式。

由于水槽的右邊界為固壁邊界,易產生反射波,本文采用阻尼消波法在水槽末端進行消波。消波段長度取為 1—2倍波長。同時,在消波區沿x軸方向采用逐漸增大的漸變網格來耗散波浪的能量。消波區網格劃分如圖 5(b)所示:z軸方向網格劃分與工作區相同,x軸方向首層網格尺寸為 2cm,后續網格尺寸按1.04的比例逐漸變大。

圖5　數值水槽網格劃分示意圖Fig.5　Grids of the numerical flume

根據內孤立波理論對振幅水深比的使用條件(黃文昊等,2013),按照不同的振幅,選取合適的理論模型,采用不同的數值造波方法進行數值模擬。具體工況如表1所示。

設置各項參數后進行流場的迭代計算,迭代時間步長取 0.01s,每個時間步長的最大迭代次數取 20次。數值計算結果如圖6、圖8所示。

3.3　計算結果與分析

圖 6為各工況下數值模擬所得波形與相應理論及實驗結果的對比。結果表明: 三種數值造波方法均能生成內孤立波,但模擬效果有差異。由工況 A1、A2、A3(B1、B2、B3 和 C1、C2、C3)可知,對于同一種振幅、同一種內孤立波理論,速度入射邊界法所模擬波形與理論及實驗波形吻合最好。平板拍擊法所模擬波形與理論及實驗波形吻合較好,只是在波形尾端存在較小的尾波,但在傳播過程中尾波會逐漸衰減,不會對內波產生影響。雙推板法所得模擬波形與理論及實驗波形趨勢相同,但最大振幅達不到設計振幅。

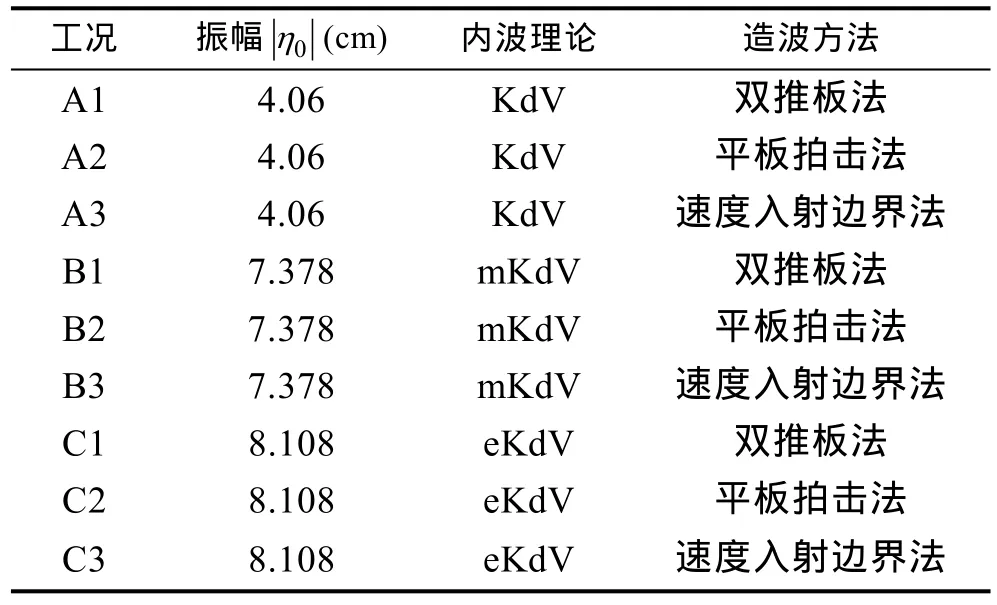
表1　數值模擬工況設置Tab.1　Condition setting of numerical simulation

由工況 A1、B1、C1(A2、B2、C2和 A3、B3、C3)可知,隨著振幅的增加,速度入射邊界法和平板拍擊法所得波形與理論及實驗波形吻合仍然較好。雙推板所得波形與理論及實驗波形趨勢仍然一致,但最大振幅與設計振幅的差值越來越大,其原因為流體阻礙了推板的運動造成耗散。由圖7(a)可知A1工況下加大推板的運動幅值后所得波形與理論及實驗波形吻合較好。因此,可通過加大推板的運動幅值使所生成內孤立波的幅值滿足要求。此外,雙推板法數值造波所得幅值還受上下層流體深度比的影響。實驗研究發現: 實測振幅均比設計振幅小,且兩者之間存在線性關系(黃文昊等,2013),因此,實際使用時需擬合相同條件下不同設計振幅與所得振幅之間的關系,然后根據實際所需振幅反算出設計振幅。

圖 6顯示三種數值造波方法結果與實驗結果存在差異,尤其隨著波高的增大,兩者的波形在末端差異越大。其原因有: (1)內波在傳播過程中粘滯效應影響會導致能量損耗。(2)實驗造波方法為重力塌陷法,波高與塌陷高度差呈正相關,塌陷高度差越大,對流體產生的激蕩也越強,引發的尾波越明顯。(3)實驗的測量設備、邊界條件等的限制導致實驗結果與數值模擬結果不能完全一致。

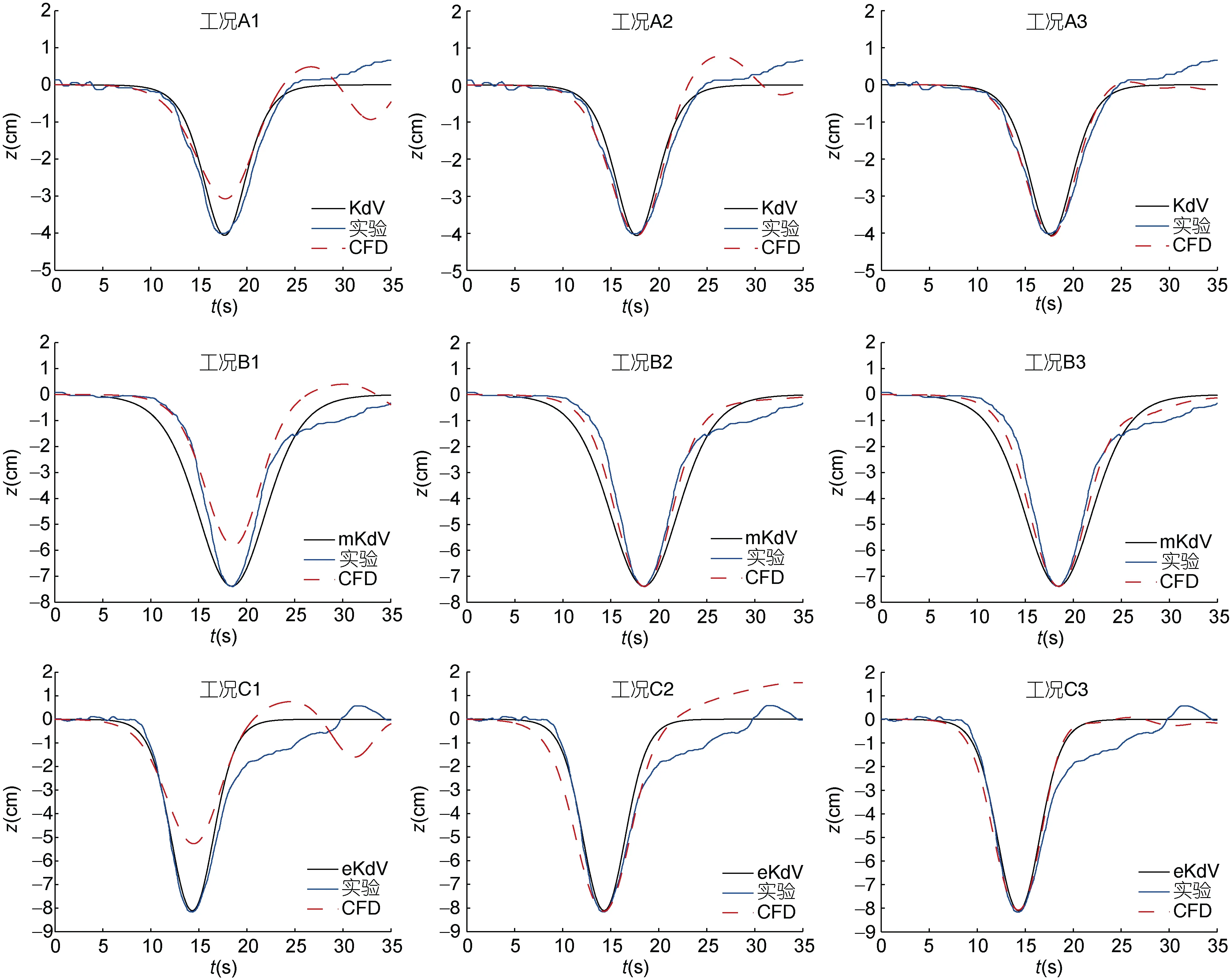
圖6　數值造波波形與理論及實驗結果對比Fig.6　Comparison in numerical waveform between experimental and theoretical results

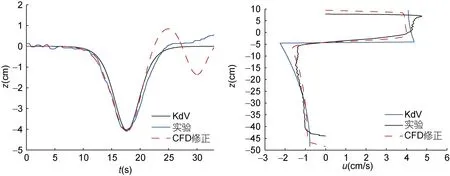
圖7　A1工況下修正后的數值造波結果與理論及實驗結果的對比Fig.7　Comparison of calibrated numerical result with experimental and theoretical ones for Case A1

由工況B1、B2、B3可知,mKdV理論波形明顯要寬于實驗波形與數值模擬波形。這一偏差說明mKdV理論對這種波高水深比情況下的內孤立波的描述存在一定偏差,但基于該理論的數值造波仍然能給出比較接近實際情況的波形。

圖 8為各工況下數值模擬所得波谷經過斷面處波致水平流速沿垂向的分布,并與理論及實驗結果進行了對比。結果表明: 三種數值造波方法所得波致水平流速沿垂向分布趨勢基本一致,但有所差異。由工況 A1、A2、A3(B1、B2、B3)可知,平板拍擊法和速度入射邊界法所得波致水平流速均與理論及實驗結果吻合較好。雙推板法所得波致水平流速相對于理論及實驗結果明顯偏小。而對于工況C1、C2、C3,由于實驗時上層流體中波致水平流速較大,致使實驗監測數據失效,實驗結果失真。但仍然可以看出速度入射邊界法和平板拍擊法所得波致水平流速與理論結果吻合較好,雙推板法與理論結果存在一定差異。

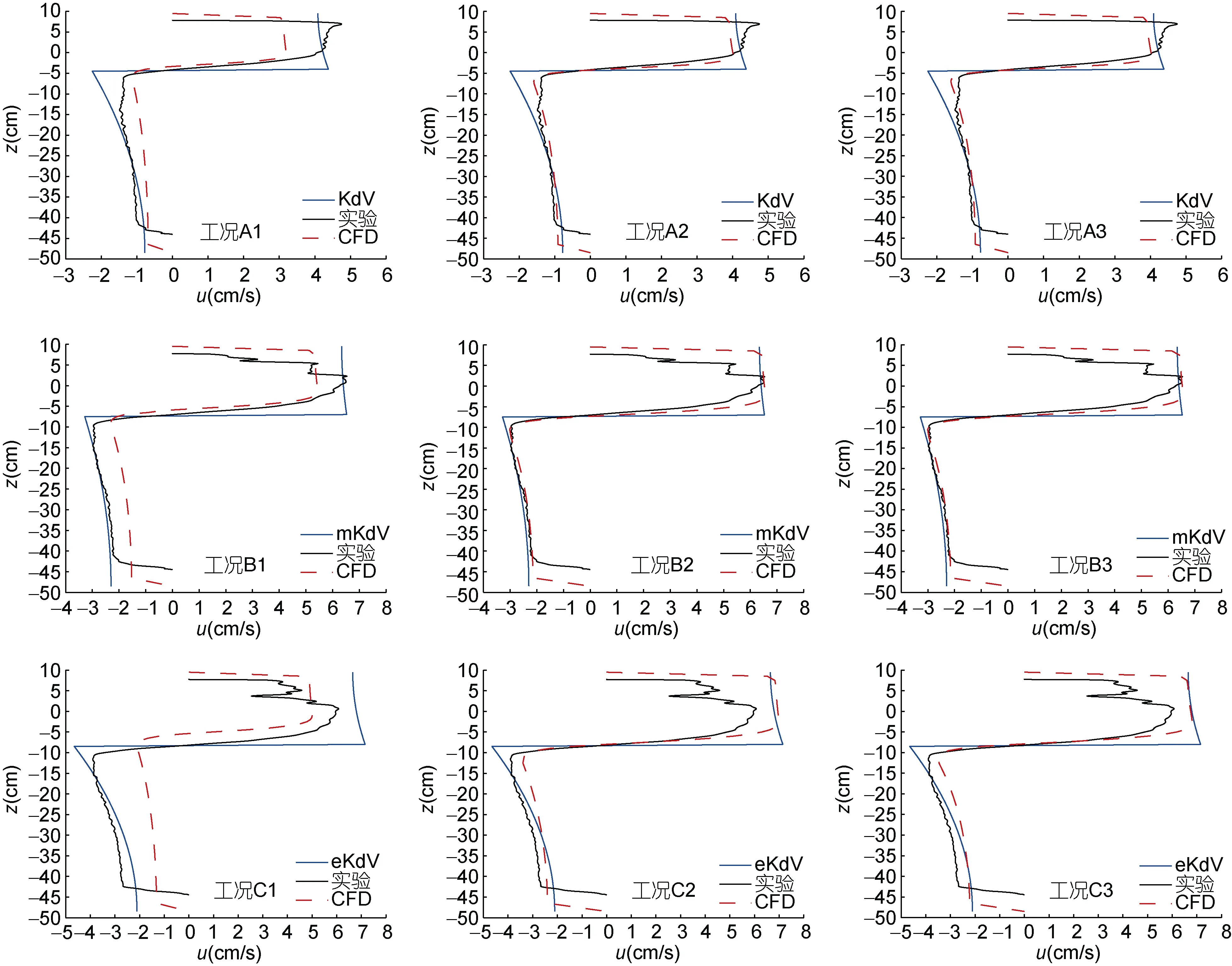
圖8　內孤立波波致水平流速沿垂向分布Fig.8　Horizontal velocity magnitude induced by internal solitary waves along vertical section

由工況 A1、B1、C1(A2、B2、C2和 A3、B3、C3)可知,隨著振幅的增加,速度入射邊界法和平板拍擊法所得結果與理論及實驗結果吻合仍然較好。雙推板法所得結果與理論及實驗結果趨勢相同,但上下層流體水平速度與理論及實驗結果的差值越來越大。加大推板的運動幅值,所得內孤立波的上下層流體水平速度與理論及實驗結果吻合較好,如圖7(b)所示。

圖8顯示實驗過程中通過PIV測量得到的上層流體水平流速變化情況比較混亂,沒有規律,與數值模擬結果存在差異,其原因為上層流體中波致水平流速較大,超出了PIV系統的測量范圍,故測得的數據存在一定失真。

內界面與波面之間區域的誤差主要原因是實驗與數值模擬存在密度躍層,密度躍層內會有流速變化,而理論模型是簡單地分為兩層處理,沒有中間過渡階段。

綜合上述分析,可以發現三種造波方法均能生成內孤立波,但雙推板法需擬合設計振幅與所需振幅之間的關系,通過加大推板的運動幅值來生成所需振幅的內孤立波,無法直接有效實現對內孤立波的數值模擬。而其余兩種數值造波方法均能直接有效模擬內孤立波的生成與傳播,且所得結果與理論及實驗結果吻合較好。

表2為三種數值造波方法模擬效率的對比。從中可以看出: 在相同電腦配置(windows 7 64位,16G內存,i7處理器)、相同振幅、相同理論模型、相同模擬時間的情況下,平板拍擊法與雙推板法所用時間相當,速度入射邊界法所用時間明顯少于前面兩種方法。其原因是仿物理造波方法使用動網格,需占用更多的計算資源。

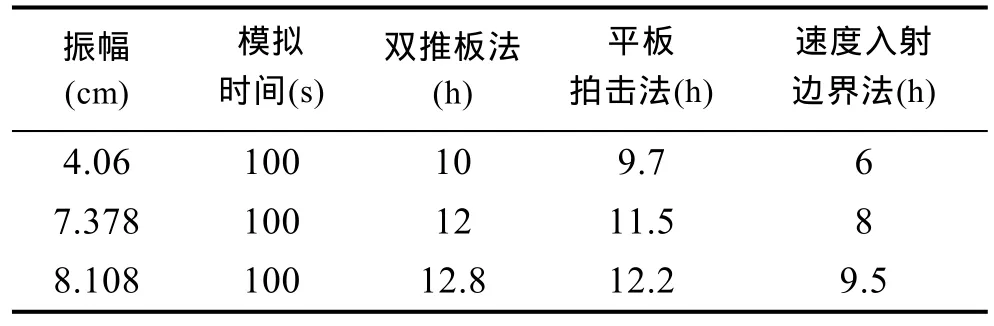
表2　三種數值造波方法模擬效率的比較Tab.2　Efficiency of three numerical wave-generating methods

4　結論

利用 Fluent軟件計算了基于 KdV、mKdV和eKdV三種理論模型與雙推板、平板拍擊和速度入口三種數值造波方法所組成的九種工況,并將模擬結果與理論及實驗結果進行對比和分析,得到如下結論:

(1) 三種數值造波方法均能實現對內孤立波的數值模擬,除雙推板法所得結果與理論及實驗結果存在一定差異,需通過加大推板的運動振幅來實現所需的造波效果外,其余兩種數值造波方法均能直接有效模擬內孤立波的生成與傳播,且所得結果與理論及實驗結果吻合較好。

(2) 雙推板法與平板拍擊法均屬于仿物理造波法,但平板拍擊法所得結果明顯優于雙推板法,因此實際使用時應優先選用平板拍擊法。

(3) 同工況同配置條件下,速度入射邊界法模擬效率最高,所得結果更準確,因此實際使用時應優先選用速度入射邊界法。

王飛,2015. 內孤立波作用下小尺度豎直圓柱體的水動力特性研究. 青島: 中國海洋大學博士學位論文,21—32

王旭,林忠義,尤云祥,2014. 兩層流體中內孤立波質量源數值造波方法. 上海交通大學學報,48(6): 850—855

方欣華,杜濤,2005. 海洋內波基礎和中國海內波. 青島:中國海洋大學出版社,1—2

付東明,尤云祥,李巍,2009. 兩層流體中內孤立波與潛體相互作用數值模擬. 海洋工程,27(3): 38—44

陳鈺,朱良生,2009. 基于Fluent的海洋內孤立波數值水槽模擬. 海洋技術,28(4): 72—75,100

高原雪,尤云祥,王旭等,2012. 基于MCC理論的內孤立波數值模擬. 海洋工程,30(4): 29—36

徐鑫哲,2012. 內波生成機理及二維內波數值水槽模型研究.哈爾濱: 哈爾濱工程大學碩士學位論文,35—36

黃文昊,尤云祥,王旭等,2013. 有限深兩層流體中內孤立波造波實驗及其理論模型. 物理學報,62(8): 084705

Choi W,Camassa R,1999. Fully nonlinear internal waves in a two-fluid system. Journal of Fluid Mechanics,396(3): 1—36

Helfrich K R,Melville W K,2006. Long nonlinear internal waves. Annual Review of Fluid Mechanics,38(1): 395—425

Michallet H,Barthélemy E,1998. Experimental study of interfacial solitary waves. Journal of Fluid Mechanics,366(1): 159—177

Osborne A R,Burch T L,1980. Internal solitons in the Andaman Sea. Science,208(4443): 451—460

Wei G,You Y X,Su X B,2009. Two-dimension numerical internal wave tank for navier-stokes equation model in the stratified fluid. In: Proceedings of the Fifth International Conference on Fluid Mechanics. Berlin Heidelberg: Springer,364—367

Zhang L,Wang L L,Yu Z Zet al,2012. Characteristics of non-linear internal waves in a three-dimensional numerical wave tank.Applied Mechanics and Materials,212—213: 1123—1130