GM(1,N)改進模型在年度售電量預測中的應用
李曉波(華南理工大學電力學院,廣東 廣州 510640)
?
GM(1,N)改進模型在年度售電量預測中的應用
李曉波
(華南理工大學電力學院,廣東 廣州 510640)
摘 要:本文基于GM(1,N)模型提出一種年度售電量預測新方法。首先對GM(1,N)模型的背景值進行修正,建立GM(1,N)改進模型;然后利用斜率關聯分析法和試探法選擇影響售電量的顯著因素。通過實際算例仿真,結果表明本文方法能夠有效提高預測精度。
關鍵詞:售電量預測;GM(1,N)模型;背景值;斜率關聯度
1 引言
隨著電力體制改革的不斷深化,電網企業越來越重視年度售電量預測工作。電網企業制定營銷決策、編制年度購電量計劃、降低供電成本等工作都離不開科學的年度售電量預測。提高年度售電量預測精度對推動電力市場發展具有深遠意義。作為灰色系統理論的重要應用,灰色預測由于其原理簡單、計算容易以及所需樣本數少等優點,在售電量預測中有很好的應用前景。其中,GM (1,1)模型是一種常用的售電量預測模型,但GM(1,1)模型將售電量當成“純粹”的數據,只分析售電量數據自身的規律,無法反映外部因素對售電量變化規律的影響,其預測結果也無法令人信服。因此有必要將售電量的影響因素引入到灰色預測模型。文獻[3]雖然將國民經濟發展加入GM(1,1)模型中,但該模型只能反映國民經濟發展單個因素對需電量的影響。文獻[4]、[5]都基于灰色關聯分析法,分別提出多因素MGM (1,N)模型和多因素灰色模型群建模法,兩種方法都綜合考慮了多種因素的影響,但未涉及顯著因素的選擇。本文提出了一種基于GM(1,N)改進模型的年度售電量預測方法。首先對GM(1,N)模型的背景值進行修正,建立GM (1,N)改進模型;其次,利用斜率關聯分析法和試探法選擇影響售電量的顯著因素;最后對地區電網企業的年度售電量進行預測分析,結果驗證了該改進模型的有效性。
2 普通GM(1,N)模型
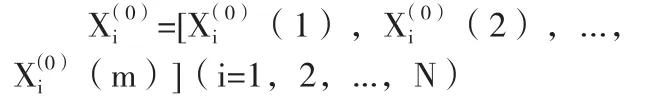
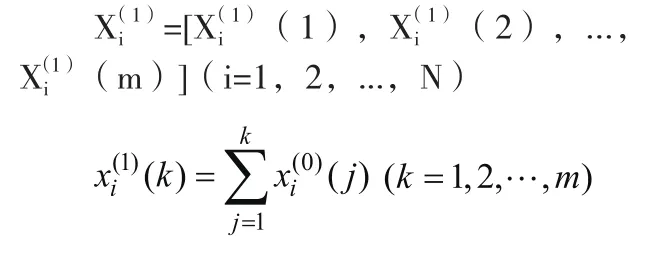
建立GM(1,N)模型,即
按最小二乘法可計算參數
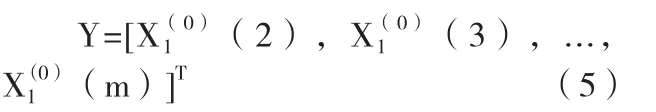
此外,GM(1,N)模型的白化方程
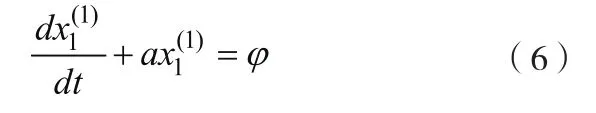
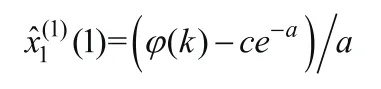
則GM(1,N)模型近似時間響應式
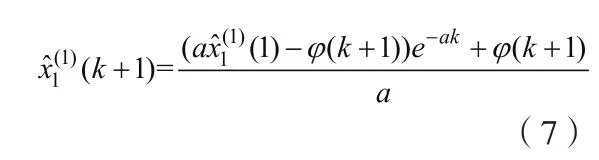
再對上式做一次累減還原,可得到售電量原始序列X1( 0)的預測模型,即
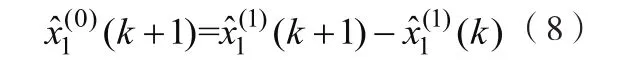
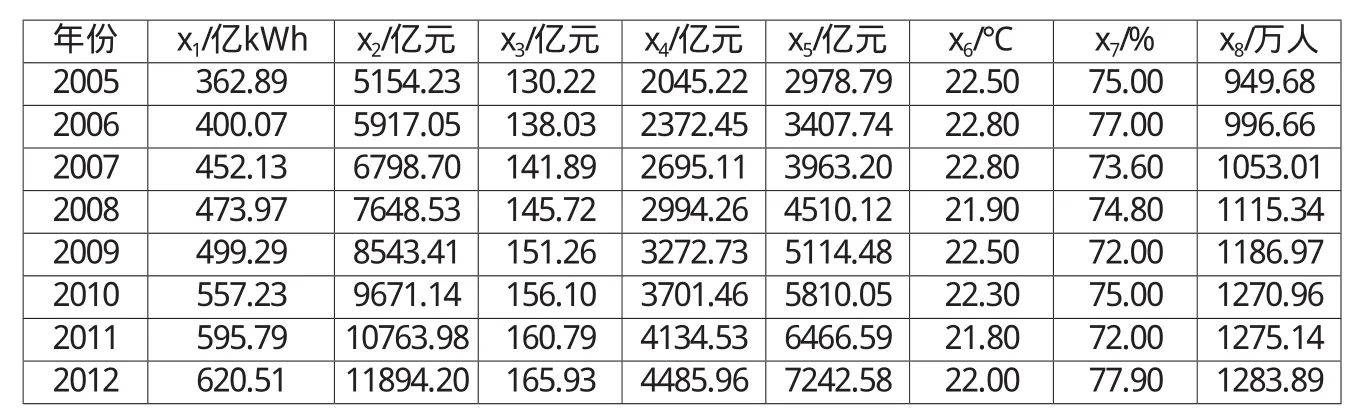
表1 售電量和影響因素歷史數據
3 GM(1,N)改進模型
文獻[6]基于建模機理的分析,指出GM(1,1)模型背景值Z(1)不應在任何情況下都為X(1)的緊鄰均值生成序列,并給出了改進的計算方法。同樣,對于GM(1,N)模型,式(2)中λ值不應一直為0.5。
由式(1)有
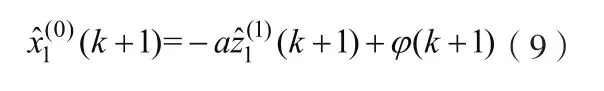
根據拉格朗日中值定理,有
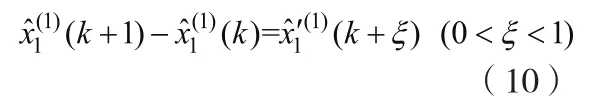
因此

由式(6)可知
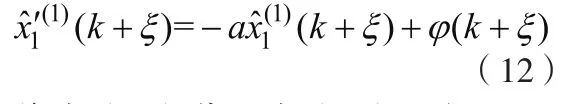
將式(12)代入式(11),得
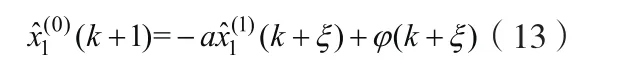
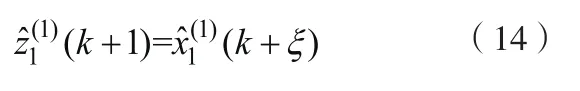
由式(7)、(8)和(13)可以計算
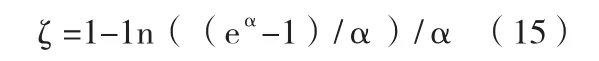
由式(2)、(7)、(14)和(15)可以計算
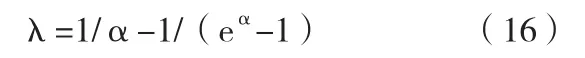
由上式可知,當|α|較小時,λ非常接近0.5;當|α|較大時,λ與0.5偏離較大。故GM(1,N)模型中λ值不應一直為0.5。對GM(1,N)模型進行背景值修正的流程如下:
①開始建立GM(1,N)模型時,λ值粗略取0.5;②由式(2)計算背景值;③由式(3)計算α值;④將上一步求得的α值代入式(16),重新計算λ值,記為λ′。如果|λ-λ′|大于設定值,則轉入步驟②,利用λ′重新計算背景值
4 選擇顯著因素
GM(1,N)模型顯著因素的選擇也直接影響到最后的預測效果。預測模型顯著因素選擇得過少,無法有效反映外部因素對售電量的影響;顯著因素選擇得過多,造成預測結果灰度過大。本文將介紹在眾多售電量影響因素中選擇與售電量密切相關的顯著因素的方法,以期GM(1,N)模型能夠達到較好的預測效果。
斜率關聯度從事物變化趨勢的斜率入手,不受事物數量級的影響,能夠很好地反映事物之間的緊密程度。因此,本文將利用斜率關聯度分析、選擇與售電量密切相關的顯著因素。斜率關聯度分析步驟如下:
(1)計算變量斜率
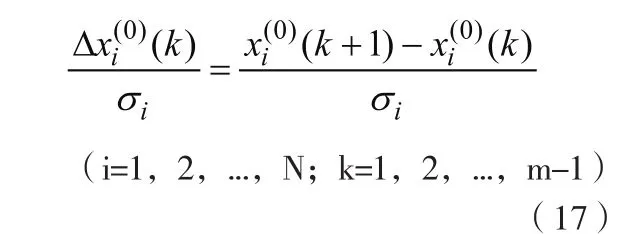
式中,σi為售電量及其影響因素原始數據的標準偏差。
(2)計算關聯系數
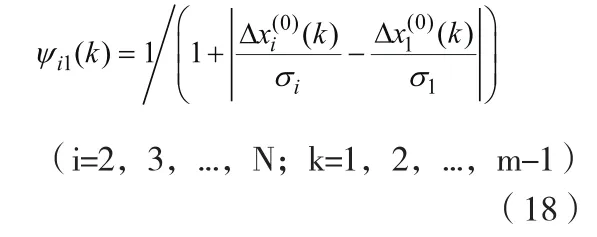
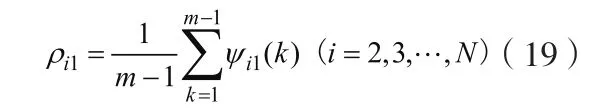
采用試探法按照售電量關聯度ρil從大到小的順序選擇顯著因素,建立GM (1,N)預測模型,并以擬合誤差極差和均方誤差作為評判模型性能標準。
5 算例分析
本文算例收集我國南方某特大城市2005~2012年全社會售電量及其影響因素的相關數據,見表1。表中售電量x1的影響因素有地區生產總值x2、第一產業生產總值x3、第二產業生產總值x4、第三產業生產總值x5、溫度x6、濕度x7和常住人口x8,其中,地區生產總值和三次產業生產總值都是按可比價格計算(基期2005年 =100)。
(1)計算斜率關聯度
計算各影響因素與售電量之間的關聯度,見表2。影響因素按關聯度從大到小排序:第二產業生產總值、地區生產總值、第三產業生產總值、第一產業生產總值、常住人口、溫度、濕度。其中,相比其它5個影響因素,溫度、濕度與售電量的關聯度過小,故在建立GM(1,N)模型過程中將不再考慮溫度和濕度。

表2 售電量和影響因素之間關聯度
從關聯度順序看出,本文所選7個影響因素中,經濟、人口對售電量影響較大,表明經濟發展越好、人口越多,全社會售電量就越多;而由于溫度、濕度的累積效應,其年平均值對售電量影響不大。
(2)選擇顯著因素
在剔除溫度、濕度以后,剩下5個對售電量影響較大的因素。下面以選擇普通GM (1,N)模型顯著因素為例進行說明,表3給出了普通GM (1,N)模型在不同影響因素情況下的擬合情況。
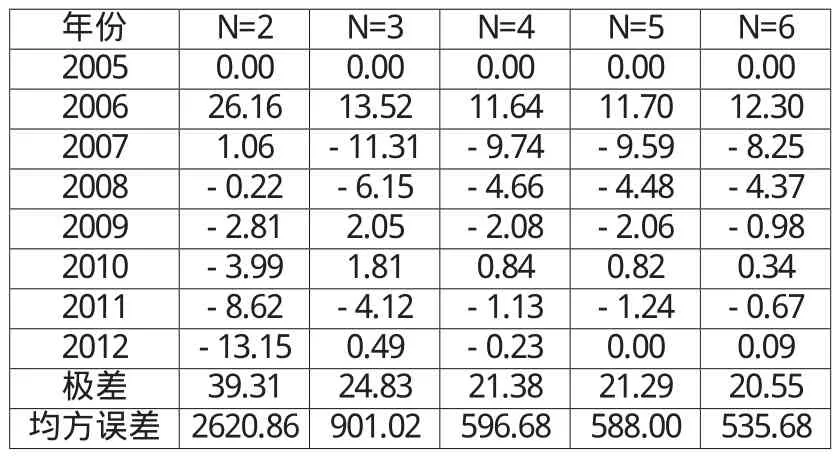
表3 不同影響因素時普通GM(1,N)模型的相對誤差(%)
表3說明了當把5個影響因素都選為模型的顯著因素時,模型的擬合效果最好,相對誤差極差、均方誤差都達到最小,并且2009~2012年的擬合相對誤差都小于1%,故可以選擇這5個顯著因素與售電量建立GM(1,6)模型。
同樣,修正背景值的GM(1,N)模型經過顯著因素選擇流程以后,也確定了這5個影響因素作為顯著因素,建立GM(1,6)模型。
(3)改進效果對比
建立普通GM(1,1)模型、普通GM(1,6)模型、和修正背景值的GM (1,6)模型,擬合效果見表4。

表4 擬合效果比較(%)
由表4可以明顯地看出,雖然普通GM(1,6)模型在前4年的擬合情況不如普通GM(1,1)模型,但是后4年的擬合情況卻比普通GM(1,1)模型好得多,并且相對擬合誤差穩定,根據“近大遠小”原則,這種情況有利于普通GM (1,6)模型對下一年的預測。此外,考慮了其它影響因素的GM(1,N)模型比GM(1,1)模型更具有說服力。
相比普通GM(1,6)模型,修正背景值的GM(1,6)模型能夠大大減小前4年的擬合誤差,同時使后4年的擬合誤差進一步減小,相對誤差極差、均方誤差指標好于普通模型,改進效果明顯。
結語
本文首先引入參數λ對GM(1,N)模型的背景值進行修正,建立GM(1,N)改進模型;其次,利用斜率關聯分析法選擇GM(1,N)模型顯著因素。在利用斜率關聯分析法從售電量影響因素中選擇顯著因素時,選擇范圍應該盡可能大,個數可以多一些,盡可能涵蓋與售電量相關的因素,以保證選擇的顯著因素不會局限在某個領域。
參考文獻
[1]段樹喬,段方婕.基于多項式回歸函數的電網公司售電量預測方法[J].數學的實踐與認識,2012,42(18):76-81. [2]彭祖贈.售電量的模糊預測[J].系統工程理論實踐,1993,13(01).
[3]張友泉.一種基于灰色系統理論的中長期需電量預測模型[J].電網技術,1999,23(08):47-50.
[4]王允平,黃殿勛,熊浩清,等.智能電網環境下采用關聯分析和多變量灰色模型的用電量預測[J].電力系統保護與控制,2012,40(01):96-100.
[5]牛東曉,張彤彤,陳立榮,等.基于關聯分析的多因素電力負荷預測灰色模型群研究[J].華北電力大學學報,2006,33(03):90-92.
[6]莊恒揚.GM(1,1)建模機理與應用條件分析及其改進方法[J].系統工程理論方法應用,1993,2(03):56-62.
[7]尹子民,羅麗兮.灰色模型GM(1,n)的變量選擇及擬合度分析[J].系統工程理論與實踐,1999.
中圖分類號:N941.5
文獻標識碼:A

