計算機博弈的研究與發展

王亞杰，邱虹坤，吳燕燕，李飛，楊周鳳

(沈陽航空航天大學 工程訓練中心，遼寧 沈陽 110136)

計算機博弈的研究與發展

王亞杰，邱虹坤，吳燕燕，李飛，楊周鳳

(沈陽航空航天大學 工程訓練中心，遼寧 沈陽 110136)

計算機博弈是人工智能領域重要而極具挑戰性的研究方向。本文首先回顧了計算機博弈的發展歷程，以及國內外的計算機博弈賽事情況，各種競賽為計算機博弈技術的發展提供了一個技術驗證與學術交流的平臺。然后介紹了計算機博弈系統的構成, 一個博弈系統包括博弈平臺、博弈樹搜索、局面評估、著法生成、機器學習等多方面技術；重點闡述了極大極小搜索、剪枝搜索、蒙特卡羅搜索等常用算法的原理與特點；對局面評估方法和各種優化算法也進行了分析，其中的并行計算、遺傳算法和基于神經網絡的深度學習算法等都是提升機器智能的有效方法。最后，分析了計算機博弈研究面臨的問題，并展望了未來的發展方向與趨勢。

人工智能；計算機博弈；蒙特卡羅搜索；神經網絡；遺傳算法；深度學習

計算機博弈，也稱之為機器博弈，是人工智能領域的挑戰性課題。它從模仿人腦智能的角度出發，以計算機下棋為研究載體，通過模擬人類棋手的思維過程，構建一種更接近人類智能的博弈信息處理系統，并可以拓展到其他相關領域，解決實際工程和科學研究領域中與博弈相關的難以解決的復雜問題[1-2]。作為人工智能研究的一個重要分支，它是檢驗計算機技術及人工智能發展水平的一個重要方向，為人工智能帶來了很多重要的方法和理論，極大地推動了科研進步，并產生了廣泛的社會影響和學術影響[3-5]。

計算機博弈是知識工程演繹的平臺，是研究人工智能科學的“果蠅”[1]。如何提高機器智能，是計算機博弈研究的精髓所在。針對該領域技術進行研究，有助于更好地理解人類的智能，更好地推動人工智能技術和相關產業的融合與發展。

1 計算機博弈發展

1.1 起步階段

20世紀50年代開始，許多世界上著名的學者都曾經涉足計算機博弈領域的研究工作，為機器博弈的研究與開發奠定了良好的基礎。阿蘭·圖靈(Alan Turing)先生最早寫下了能夠讓機器下棋的指令，計算機之父馮·諾依曼(John von Neumann)提出了用于博弈的極大極小定理，信息論創始人科勞德·香農[6](Claude E. Shannon)首次提出了國際象棋的解決方案，人工智能的創始人麥卡錫(John McCarthy)首次提出“人工智能”(artificial intelligence)這一概念。1958年阿伯恩斯坦(Alex Bernstein)等[7]在IBM704機上開發了第1個成熟的達到孩童博弈水平的國際象棋程序。1959年，人工智能的創始人之一塞繆[8](A.L. Samuel)編了一個能夠戰勝設計者本人的西洋跳棋程序，1962年該程序擊敗了美國的一個州冠軍。

研究機器博弈的學者們發現，博弈程序的智能水平與搜索深度有很大關系。他們研究的內容主要涉及：如何建立有效、快速的評價函數和評價方法，使評價的效率更高，花費的時間和空間的代價更小；如何在生成的博弈樹上更準確有效地找到最優解，并由此發展出來各種搜索算法[9-11]。

1.2 發展階段

20世紀80年代末，隨著計算機硬件和軟件技術不斷發展，計算機博弈理論日趨完善，學者們開始對電腦能否戰勝人腦這個話題產生了濃厚的興趣，并提出了以棋類對弈的方式，向人類發起挑戰，計算機博弈研究進入了快速發展的階段。

在國外，1986年7月，Hinton等[12]在自然雜志(Nature)上發表論文，首次系統簡潔地闡述了反向傳播算法在神經網絡模型上的應用，給機器學習帶來了希望，掀起了基于統計模型的機器學習熱潮。1989年IBM公司研制的“深思”在與世界棋王卡斯帕羅夫進行的“人機大戰”中，以0∶2敗北。1995年IBM更新了“深藍”程序，并使用新的集成電路將思考速度提高到每秒300萬步，在1996年與卡斯帕羅夫的挑戰賽中以2∶4敗北。1997年“超級深藍”融入了更深的開發，以3.5∶2.5擊敗了卡斯帕羅夫，這場勝利引起了世界范圍內的轟動，它表明“計算機智能戰勝了人類天才”。

在國內，南開大學黃云龍教授和他的學生在20世紀80年代，開發了一系列中國象棋程序。中山大學化學系教授陳志行先生在90年代初開發了圍棋程序“手談”，曾經獲得世界冠軍。

1.3 成熟階段

20世紀末期，國內外有許多科研機構和學者在計算機博弈領域進行深入探討和實質性的研究。隨著極大極小算法(minimax algorithm)[11]、α-β剪枝[9,11]、上限置信區間算法(upper confidence bound apply to tree，UCT)[13]、并行搜索算法[14]、遺傳算法[15]、人工神經網絡[16]等技術日趨成熟，人工神經網絡、類腦思維等科學也不斷取得突破性進展，各種機器學習模型，例如支持向量機、 Boosting算法、最大熵方法等相繼被提出，計算機博弈研究進入了一個前所未有的階段。

2006年，Hinton和他的學生在Science上發表了一篇關于用神經網絡降低數據維數的論文[16]，開啟了深度學習在學術界的浪潮。2007年科學雜志評出的人類10大科學突破中，包括了加拿大阿爾波特大學研究人員歷時18年破解了國際跳棋(64)的研究成果，這是整個機器博弈發展史上的一個里程碑[5]。

2003年，臺灣交通大學吳毅成教授發明了六子棋 (connect 6)[ 17 ]，目前被認為是最公平的棋類。之后，東北大學徐心和教授[ 18 ]和他的團隊[19-21]研究開發了中國象棋軟件“棋天大圣”，具有挑戰國內中國象棋頂級高手的實力；北郵劉知青[22-23]帶領學生開發的“本手(LINGO)”圍棋程序，能夠戰勝高水平業余圍棋選手；哈工大王軒[24-26]、南航夏正友[27-28]分別帶領學生開發了四國軍棋博弈系統，這些程序都表現出較高的智能水平。

1.4 飛躍階段

最近幾年，基于人工神經網絡[3]取得了突破性的進展。運用該技術，成功地解決了計算機博弈領域中許多實際問題。

2012年6月，谷歌公司的Google Brain項目用并行計算平臺訓練一種稱為“深度神經網絡”(deep neural networks，DNN)的機器學習模型。2013年1月，百度宣布成立“深度學習研究所”(institue of deep learning，IDL)。在2015年10月5∶0擊敗了歐洲圍棋冠軍樊麾后，2016年1月，谷歌DeepMind團隊在自然雜志(Nature)上發表封面論文稱，他們研發出基于神經網絡進行深度學習的人工智能圍棋程序AlphaGo，能夠在極其復雜的圍棋游戲中戰勝專家級人類選手[3]。2016年3月，AlphaGo又以4∶1戰勝世界圍棋冠軍李世石，在學術界產生了空前的影響，這標志著計算機博弈技術取得重大成功，是計算機博弈發展史上新的躍遷。

2 賽事與學術交流

由國際機器博弈協會(International Computer Games Association，ICGA)組織的國際計算機博弈比賽(Computer Olympiad，CO)每年一屆，已經有了30多年的歷史。比賽項目包括中國象棋、六子棋、亞馬遜棋、圍棋等，通過競賽促進了世界范圍內的計算機博弈技術的發展。同時，ICGA還每年組織學術研討會，并出版ICGA季刊[27,30-32]。

從1969年開始，國際人工智能聯合會議(International Joint Conference on Artificial Intelligence，IJCAI)每兩年舉行一次，IJCAI是人工智能研究人員最主要國際會議之一。通過學術交流，發表計算機博弈的最新研究成果[33-35]。

2006年8月，由中國人工智能學會首次主辦中國計算機博弈錦標賽，至今已舉辦10屆。從2011年開始，由中國人工智能學會與教育部高等學校計算機類專業教學指導委員會共同主辦全國大學生計算機博弈大賽暨全國錦標賽[36-37]，目前已舉辦6屆。這項賽事所設定的各項比賽，涉及計算機博弈相關的知識庫、博弈平臺[38]、搜索引擎、神經網絡、機器學習與局面評估[39-40]等多種技術，吸引了越來越多的專家、學者與計算機博弈愛好者參與到計算機博弈相關研究中，為計算機博弈技術的交流與驗證提供了一個公平、開放的平臺。目前，競賽項目涵蓋了多種類型的博弈：

1)按參與人數劃分，包括雙人博弈[41](如中國象棋、圍棋)和多人博弈(如二打一撲克[42])；

2)按參與人對他人了解程度劃分，包括完備信息博弈[43](如中國象棋、圍棋、六子棋、亞馬遜棋、蘇拉卡爾塔棋等)和非完全信息博弈[24,44](如幻影圍棋、軍棋、二打一撲克)；

3)按參與人之間有無合作劃分，包括合作博弈(如橋牌[45])與非合作博弈(如中國象棋)。

除了以上競賽，還有各種世界范圍內的人機大戰活動，這些競賽活動極大地激發了人們的挑戰熱情和創新精神，為社會培養了大量的科技精英，在促進了人工智能技術快速發展的同時，還產生了新的科研成果。

3 計算機博弈系統設計

計算機博弈系統是指在特定規則下具有博弈能力的智能系統。在設計系統時，需要考慮知識表示、著法產生、搜索與評估幾個方面。

典型的計算機博弈系統的核心架構設計如圖1所示，可以劃分為博弈平臺和搜索引擎兩大模塊。其中，博弈平臺主要負責界面顯示、棋規判斷、行棋過程控制、信息傳遞等[38]，在其設計過程中，通常考慮通用性、易用性、健壯性、藝術性；博弈引擎主要負責知識學習、開(或殘)局庫設計[20,46]、棋局評估、博弈樹搜索、著法生成等。

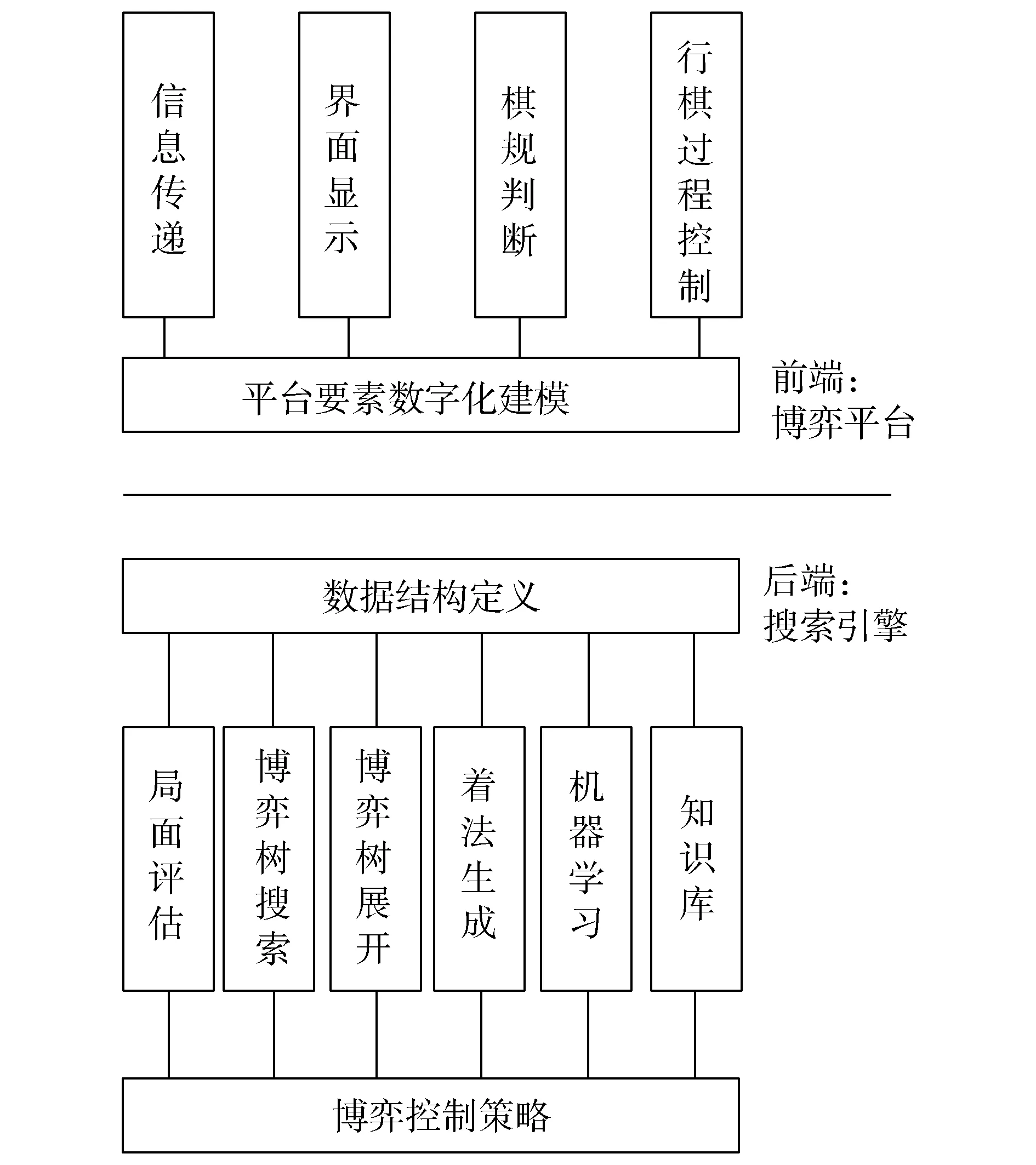
圖1 計算機博弈系統典型架構Fig.1 Typical architecture of computer game system

相對整個計算機博弈系統而言，后端搜索引擎是整個系統的核心部分，它是決定博弈勝負的關鍵，在搜索引擎的開發過程中，除了考慮與博弈平臺的接口外，還要根據各個棋種的特點，選擇合適的搜索算法和評估函數[47-48]。

4 博弈樹搜索技術

4.1 博弈樹復雜度

博弈樹是由樹枝和節點構成單向無環圖，如圖2所示。博弈樹的節點對應于某一個棋局，其分支表示走一步棋；根部對應于開始位置，其葉表示對弈到此結束。生成博弈著法的過程，對應博弈樹的搜索與展開[49]。計算機博弈的過程是雙方輪流給出著法，使棋局向著對本方有利的方向發展，直至最后的勝利。

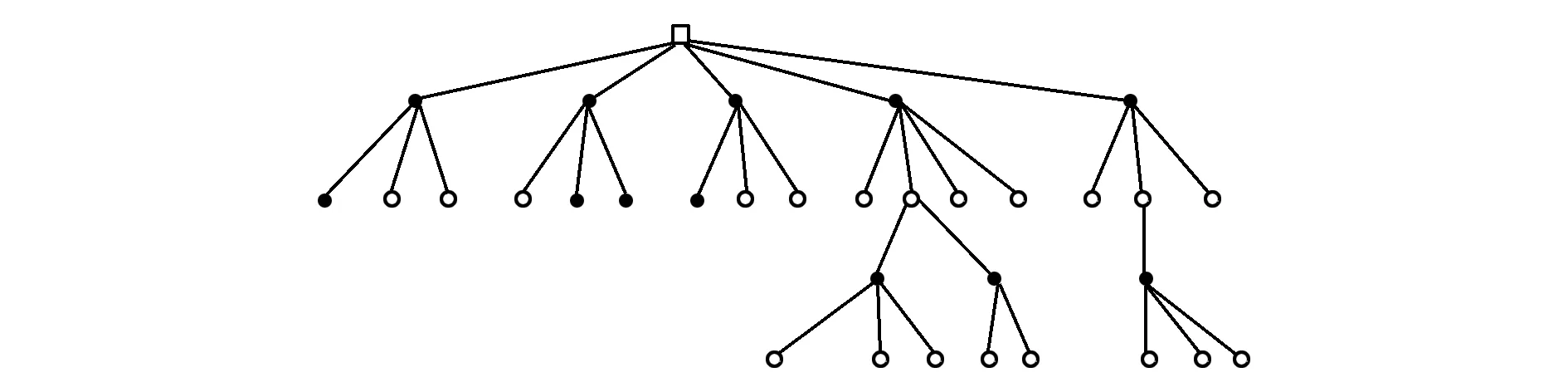
圖2 博弈樹示意圖Fig.2 Schematic diagram of game tree

搜索博弈樹的目的就是在假設雙方的走法都是最佳的情況下，找到從根節點到葉子節點的最佳路徑，找出當前的最佳著法。

博弈樹中的每個葉節點，都可以用評估函數來對其優劣進行評分，該值對于博弈雙方都是最優的。博弈樹的子樹在搜索完成之后會返回一個博弈值，該值對于該子樹是局部最優解，但是對整個博弈樹來說并不一定是全局最優解。

在計算機博弈研究中，求解過程中計算復雜性是個難以逾越的難題。對于NP-complete、PSPACE-complete及EXPTIME-complete等難解的問題，不必將大量的精力花費在尋找問題的解析解上，而只能去尋求某種近似解。國內外學者對計算機博弈的計算復雜性[50-51]進行研究，證明了國際象棋和西洋跳棋屬于EXPTIME-complete問題，圍棋屬于PSPACE-hard問題，中國象棋屬于EXPTIME-complete問題[52]。

對于許多棋種而言，一棵完整博弈樹的規模非常龐大，可以達到相當可觀的天文數字，表1中列出幾種知名棋種的復雜度[53]。

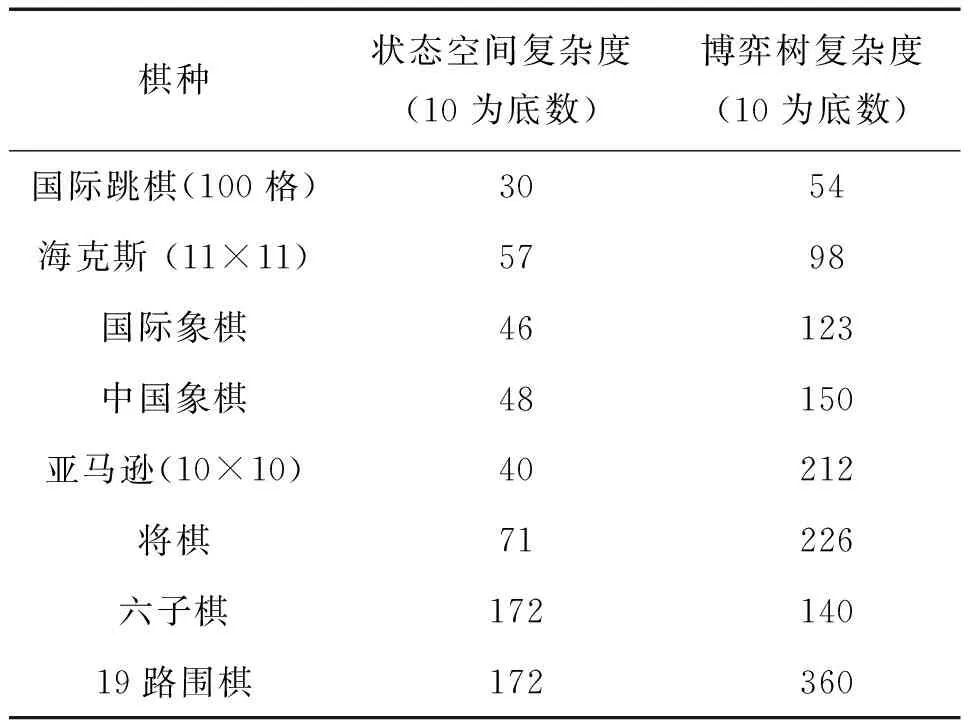
表1 幾種知名棋類的復雜度

顯然，把搜索樹修整到合理范圍內，減少其搜索空間，能夠有效地進行展開和遍歷搜索。

4.2 博弈樹搜索

以中國象棋、國際跳棋為代表的二人零和完備信息博弈，其搜索理論已經很系統。其中極大極小算法[53]是最基本的搜索算法，它奠定了計算機博弈的理論基礎。以極大極小算法為基礎的博弈樹搜索算法，從搜索方向考慮，可以分為深度優先搜索和寬度優先搜索；從控制策略考慮，可以分為盲目搜索和啟發搜索；從搜索范圍考慮，可以分為窮盡搜索、裁剪搜索。

相對而言，寬度優先搜索、窮盡搜索和盲目搜索算法時間和空間開銷巨大，難以做到很深的搜索。因此，在計算機博弈的實際應用中，很少直接使用此類算法解決問題。

4.2.1 窮盡搜索

極大極小算法[54]是典型的窮盡搜索方法，通過它可以找到對于博弈雙方都是最優的博弈值，但該算法對博弈樹的搜索是一種變性搜索，算法實現相對麻煩。

負極大值算法在極大極小算法基礎上進行了改進，把極小節點值(返回給搜索引擎的局面估值)取絕對值，這樣每次遞歸都選取最大值。

4.2.2 裁剪搜索

裁剪算法也稱剪枝算法，是計算機博弈中最常用的主流算法，它包括深度優先的Alpha-Beta剪枝搜索[9]和以此為基礎改進與增強的算法，如渴望窗口搜索(aspiration search)[55]、MTD(f)(memory-enhancedtestdriverwithfandn)搜索[56]等。在具體應用中，合理地交叉使用各種搜索方法，可以具有更高的效率[56]。

1)Alpha-Beta剪枝[9,33]

Alpha-Beta剪枝是在極大極小算法基礎上的改進算法，是其他剪枝算法的基礎。目前，多數博弈程序都采用負極大值形式的Alpha-Beta搜索算法。為保證Alpha-Beta搜索算法的效率，需要調整樹的結構，即對搜索節點排序，確保盡早剪枝。

2)渴望搜索[54-55]

渴望搜索是在Alpha-Beta搜索算法基礎上，縮小搜索范圍的改進算法。渴望搜索從一開始就使用小的窗口，從而在搜索之初，就可以進行大量的剪枝。通常，渴望搜索與遍歷深化技術結合使用，以提高搜索性能。

3)MTD(f)搜索[56]

MTD(f)搜索實際上就是不斷應用零窗口的Alpha-Beta搜索，縮小上界和下界，并移動初始值使其接近最優著法。MTD(f)算法簡單高效，在國際象棋、國際跳棋等博弈程序里，MTD(f) 算法平均表現出色。

此外，還有各種在Alpha-Beta搜索基礎上優化的算法，例如，有學者提出在博弈樹同層結點中，用廣度優先搜索，接力式空窗探測，平均搜索效率高于MTD(f)搜索[57]。通常，裁剪算法需要與置換表技術相結合，以減少博弈樹的規模，提高搜索效率。

4.2.3 置換表[58]技術

置換表是一個大的直接訪問表，用來存儲已經搜索過結點(或者子樹)的結果，下次搜索遇到時直接運用。置換表的構造，一般使用Hash表和ZobristHash技術來實現。

合理使用置換表，可以提高搜索效率，當博弈樹的深度很大時，置換表對內存空間要求巨大。通常的對策是對置換表分配有限大小，并采用散列方式管理存取。具體應用到各個棋種中時，還要根據實際局面的節點類型，進行處理。

4.2.4 啟發式算法

“啟發”(Heuristic)是指通過排序讓Alpha-Beta剪枝的搜索樹盡可能地接近最小樹，優先搜索好的著法。啟發通常有置換表啟發、歷史啟發和殺手啟發等常用的算法。

1)置換表啟發[58-59]

置換表啟發是置換表與Alpha-Beta剪枝算法相結合的產物。在中國象棋等棋種中，通過引進置換表啟發技術來增強搜索效率。

2)歷史啟發[60]

歷史啟發也是迎合alpha-beta搜索對節點排列順序敏感的特點來提高剪枝效率的。它通過維護著法歷史，每當遇到好的著法，就給其歷史得分一個相應的增量，使其具有更高的優先被搜索的權利。

歷史啟發是一種基于經驗的擇序標準，它克服了基于知識擇序存在的知識不足的缺點，使得算法的擇序具有很強的動態適應性。

3)殺手啟發[61]

殺手啟發可以看作是歷史啟發的特例。它把同層中引發剪枝最多的節點稱為殺手，當下次搜索到同一層時，如果殺手移動是合法的話，就優先搜索殺手。殺手啟發可以對著法進行動態重排序，且提高了置換表的使用效率。

4.2.5 迭代深化[62]

迭代深化也稱為遍歷深化，是一種常用的蠻力搜索機制，經常使用在深度優先搜索中。迭代深化最初是作為控制時間的機制而提出的，通過對博弈樹進行多次遍歷，并逐漸提高搜索深度，一直到指定的時間停止。

迭代深化利用Alpha-Beta剪枝算法對子節點排序敏感的特點，使用上次迭代后得到的博弈值，作為當前迭代的搜索窗口估值，以此為啟發式信息計算當前迭代的博弈值。另外，它利用時間控制遍歷次數，只要時間一到，搜索立即停止。在關鍵的開局和殘局，由于分支較少，可以進行較深層次的搜索。Alpha-Beta剪枝經過一系列技術如置換表、歷史啟發、迭代深化等增強后，其性能可大幅提高。

4.2.6 最佳優先算法

最佳優先的搜索算法，不受節點排序的影響，其搜索空間小于深度優先的最小樹，理論上應該優于深度優先。實際上，最佳優先算法仍處于理論研究階段。最佳優先算法分為兩類：采用極大極小算法取值的SSS*[63-64]算法和DUAL*算法，不采用極大極小方法取值的B*[65]和PB*[66]算法。

1)SSS*和DUAL*算法[63-64]

SSS*和DUAL*算法都屬于狀態空間搜索(StateSpaceSearch)，把極大極小樹看成狀態圖，在不同的分支上展開多條路徑，并且維護一個關于狀態圖的全局信息表。這兩種算法是兩個操作相反的過程，前者在搜索深度為偶數的極大極小搜索中表現較佳，后者則在深度為奇數搜索中較佳。

SSS*和DUAL*算法都過于復雜，難于理解，且時間和空間開銷較大，在計算機博弈中實際應用較少。

2)B*和PB*算法[65-66]

B*算法用一個樂觀值和一個悲觀值來評價節點。當根節點的一個孩子的悲觀值不比所有其他節點的樂觀值差的時候，B*算法就結束了。算法搜索控制的關鍵是盡快找到終止條件。由于它對局面估值的依賴性太強，估值的可信度將直接影響最終結果。

PB*算法就是基于概率的B*算法，這個算法對概率的準確估計比較敏感，實現困難。

4.2.7 隨機搜索

隨機搜索有兩種算法：拉斯維加斯算法和蒙特卡羅算法。采樣越多，前者越有機會找到最優解，后者則越接近最優解。

通常，要根據問題的約束條件來確定隨機算法，如果對采樣沒有限制，但必須給出最優解，則采用拉斯維加斯算法。反之，如果要求在有限采樣內求解，但不要求是最優解，則采用蒙特卡羅算法。

計算機博弈中，每步著法的運算時間、堆棧空間都是有限的，且僅要求局部優解，適合采用蒙特卡羅算法。由于非完備信息博弈也具有不確定性博弈的一些特征，所以蒙特卡羅算法也適用于非完備信息博弈。

1)蒙特卡羅搜索(MCTS，MonteCarloTreeSearch)[67-70]

在人工智能的問題中，蒙特卡羅搜索是一種最優決策方法，它結合了隨機模擬的一般性和樹搜索的準確性。由于海量搜索空間、評估棋局和落子行為的難度，圍棋長期以來被視為人工智能領域最具挑戰的經典游戲。近年來，MCTS在類似計算機圍棋等完備信息博弈、多人博弈以及其他隨機類博弈難題上的成功應用而受到快速關注[71]。理論上，MCTS可以被用在以{狀態，行動}定義并用模擬預測輸出結果的任何領域。

基本的MCTS算法根據模擬的輸出結果，按照節點構造博弈樹，其過程如圖3所示，包括路徑選擇(Selection)、節點擴展(Expansion)、模擬實驗(Simulation)、反向傳播(Backpropagation)4個步驟。

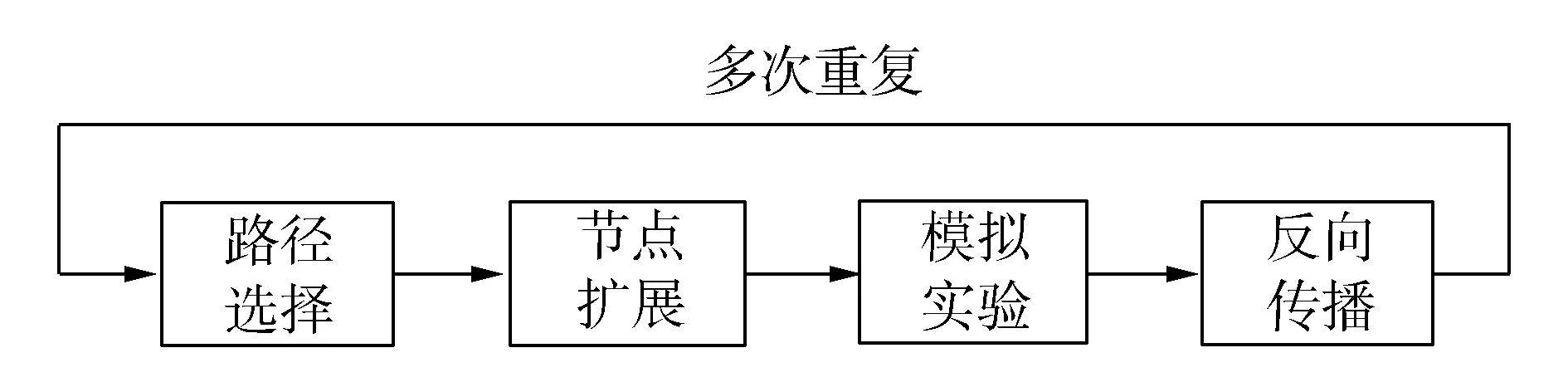
圖3 構造MCTS博弈樹的過程Fig.3 Process of constructing the MCTS game tree

MCTS算法適用于有較大分支因子的博弈程序，如AlphaGo就是采用MCTS算法進行搜索[3]。

2)UCT算法[13,25]

UCT算法，即上限置信區間算法，是一種基于MCTS發展的博弈樹搜索算法，該算法通過擴展UCB(upperconfidencebound)到極大極小樹搜索，將MCTS方法與UCB公式結合。

UCB計算方法如公式1所示，在向下遍歷博弈樹時，通過選擇最大化該值來實現節點的選擇。

(1)

式中：vi是節點i估計的值，ni是節點i被訪問的次數，而N是其父節點已被訪問的總次數，C是可調參數。相對于傳統的搜索算法，UCT時間可控，具有更好的魯棒性，可以非對稱動態擴展博弈樹，在超大規模博弈樹的搜索過程中，表現出時間和空間方面的優勢。目前，UCT在搜索規模較大的完備信息博弈、復雜的多人博弈、非完備信息博弈以及隨機類博弈項目中，表現出色[71]。

5 局面評估

在計算機博弈系統中，對博弈局面評估得越全面、越準確，獲勝的機率就會越高。但是，博弈有個很重要的約束條件就是時間。評估中考慮的問題越全面細致，則耗費的時間就越多，搜索的深度和速度必然受到影響。另外，隨著搜索深度加深，信息處理量也會大幅提升。

設計評估函數需要考慮諸多因素，在完全信息博弈中雙方的子力、領地、位置、空間、機動性、拍節、威脅、形狀、圖案都可以作為評估參數，非完備信息博弈中除了己方已知參數外，還要猜測對手的情況，并通過量化后加權組合而成。

國內外有不少學者在計算機博弈評估方面做了大量深入研究[72]。針對不同棋種的特點，學者們提出了各種不同的方式進行評估與優化：通過博弈記錄來評估博弈樹搜索[73]；針對六子棋應用遺傳算法進行尋優處理，優化機器博弈評估函數[40]；在中國象棋里，把自適應遺傳算法引入評估函數中，通過錦標賽算法對評估函數中的參數組合進行自動調整和優化[19]；根據棋子的數量、移動范圍、攻擊范圍、子力攻擊力、盤面分值和占弧價值等對蘇拉卡爾塔棋局面評估函數進行了研究[40]；根據亞馬遜棋領地、位置和機動性等特征在不同階段的重要程度及權重值，給出一個分階段的評估函數[47,74]。

提高計算機博弈能力不能單純依靠加大搜索深度，還需要將必要的相關博弈知識引入到相應的博弈搜索中，只有協調搜索算法與評估函數，博弈系統才能發揮有效作用。

6 綜合優化技術

計算機博弈中，目前應用較多的綜合優化技術主要有并行計算、遺傳算法和基于神經網絡的深度學習。

6.1 并行計算

并行計算[14,75]是為了提高計算速度，把博弈樹動態分開，發揮計算機多CPU強大的并行處理能力，同時執行多個指令的算法。它不裁剪和縮小博弈樹的規模，通過提高搜索速度，而進行優化系統。

并行計算有兩種體系，單機體系SMP(SymmetricMultiprocessor)和分布式體系Cluster(計算機集群)，對應多線程并行和多機并行。兩者最大的區別是，前者可以共享存儲器(并且共享同一地址的存儲單元)，后者則必須通過網絡來交換數據。由于博弈搜索通常需要用到置換表，所以適合以SMP的方式多線程并行處理，但隨著大數據、云計算等技術的成熟與完善，計算機集群技術將被越來越多地運用到計算機博弈中。

6.2 遺傳算法

遺傳算法[15]是人工智能領域的關鍵技術，它是一種非數值、并行、隨機優化、搜索啟發式的算法，通過模擬自然進化過程隨機化搜索最優解。它采用概率化的尋優方法，能自動獲取和指導優化的搜索空間，自適應地調整搜索方向，不需要確定的規則，同時具有內在的隱并行性和更好的全局尋優能力。

遺傳算法是解決搜索問題的一種通用算法，在計算機博弈中，遺傳算法通常被用于搜索、自適應調整和優化局面評估參數。它的基本思想是將博弈樹看作遺傳操作的種群，博弈樹中由根節點到葉子節點組成的所有子樹為種群中的個體。根據優化目標設計評估函數，計算種群中每個個體的適應度函數值，依據適應度函數值的大小確定初始種群，讓適應性強(適應度函數值大)的個體獲得較多的交叉、遺傳機會，生成新的子代個體，通過反復迭代，可得到滿意解。

采用遺傳算法優化局面估值時，可根據博弈程序與其他程序對弈的結果，檢驗某一組參數獲勝的機率。經過多次試驗，通常可以找到較好的估值參數。傳統的算法一般只能維護一組最優解，遺傳算法可以同時維護多組最優解。在實踐中，遺傳算法被引入了中國象棋、國際象棋、亞馬遜等棋搜索與評估優化中，效果還是很明顯的[19]。

6.3 深度學習

深度學習是基于多層網絡結構的一種機器學習方法，它逐層提取抽象特征，通過多層非線性傳輸，完成復雜的目標函數系統逼近。深度學習領域典型的網絡模型包括卷積神經網絡(convolutionalneuralnetworks，CNN)、深層玻爾茲曼機(deepboltzmannmachine，DBM)和堆疊自動編碼器(stackedauto-encoder，SAE)等[76]。

近幾年，基于人工神經網絡的深度學習技術逐漸被應用于計算機博弈中[3,29]，人工智能圍棋程序AlphaGo是其典型代表[3]。AlphaGo成功的關鍵在于擁有兩個大腦——落子選擇器(movepicker)和棋局評估器(positionevaluator)。分別基于兩種不同的深度神經網絡——策略網絡(policynetwork)和價值網絡(valuenetwork)，如圖4所示。前者用于學習高水平棋手的棋譜，獲得如何在盤面落子的棋感；后者通過機器的增強型學習，獲得形勢判斷的棋感。這兩個棋感通過蒙特卡羅搜索的技術進行驗證，使AlphaGo實現了技術突破。

盡管深度學習技術在圍棋方面取得了前所未有的成功，但在拓展應用方面，如何合理利用深度學習方法來增強傳統學習算法的性能，提升計算機博弈水平，仍是今后研究的重點。

圖4 AlphaGo神經網絡體系結構原理圖Fig.4 Schematic representation of the neural network architecture used in AlphaGo

7 面臨的問題與展望

近年來，計算機博弈給人工智能帶來了很多重要的方法和理論，在二人零和完備信息博弈研究方面，其知識結構系統層次清晰，已經取得了許多驚人的成果，其中，關于基于神經網絡深度學習技術的研究與運用，已經達到新的高度。在中國象棋、圍棋等完全信息的計算機博弈中，盡管狀態空間和搜索樹復雜度都較大，但經過大量學習與訓練，結合大規模搜索算法，計算機占盡優勢[78]。

另一個方面，對于軍棋、麻將、橋牌、撲克等非完備信息博弈，以及具有模糊性和隨機性的不確定性博弈，雖然在基于案例的策略研究方面有了一定進展，但因其相關理論研究還不成熟，相應的程序智力有限，仍難以戰勝人類真正的高手。因此，在非完備信息和不確定性機器博弈方面，具有高效學習與抽象思維能力的博弈技術還有待進一步研究。另外，在計算機博弈平臺方面的研究投入相對較少，對計算機博弈技術的發展也有所制約。

可以預見，在不遠的將來，計算機博弈技術將融入各個領域的應用中，具體體現在如下幾點：

1)計算機博弈研究的內容將不斷拓寬，處理的問題復雜程度越來越高，信息量將越來越大。為解決某類特定問題，技術方法將集成化，計算機博弈技術將與并行計算、大數據技術等相關技術結合。

2)計算機博弈軟件與硬件的結合越來越密切，固化博弈系統的智能硬件產品將越來越多地出現在人們的生活中，典型的應用包括：有博弈思維能力機器人、智能決策控制系統的無人駕駛汽車和無人機。

3)計算機博弈技術將與其他學科進一步融合，越來越緊密地應用經濟、生活、軍事等領域，注重實際工程應用，解決實際問題。在虛擬現實仿真方面，特別是游戲與教育方面擁有廣闊的應用前景。

4)計算機博弈技術將呈現高度智能化趨勢，通過與遺傳算法、人工神經網絡、類腦思維等人工智能技術進一步融合，類似基于神經網絡深度學習的智能技術將大量涌現，使得計算機博弈程序的類腦智能越來越高。

5)合理拓展現有的博弈技術，深入研究更加智能的普適算法，構建一個通用的計算機博弈系統，也將成為未來計算機博弈研究的重點。

8 結束語

伴隨著人工智能科學發展的60周年，計算機博弈也經歷了起步、發展、成熟、飛躍4個階段。依托各種形式的競賽，極大地促進了學術交流，檢驗了新技術，推動了博弈的研究與發展。當前完備信息博弈技術相對比較成熟，非完備信息博弈和隨機類博弈技術還需進一步發展。深度學習算法在AlphaGo圍棋計算機博弈中的成功應用，引發了世界范圍內對人工智能技術的高度關注，調動了更多的專家學者開展深入研究的積極性。盡管在計算機博弈領域還存在著各種各樣的問題，許多工作還需要向更廣領域和更深層次推進，但是隨著研究人員的不斷增加以及計算機博弈技術在各個領域的廣泛應用，將會產生越來越多的研究成果。計算機博弈是一個頗有發展前途的研究領域。

[1]徐心和, 鄧志立, 王驕, 等. 機器博弈研究面臨的各種挑戰[J]. 智能系統學報, 2008, 3(4): 288-293.XUXinhe,DENGZhili,WANGJiao,etal.Challengingissuesfacingcomputergameresearch[J].CAAItransactionsonintelligentsystems, 2008, 3(4): 288-293.

[2]徐心和. 計算機博弈——對于人類思維的挑戰[J]. 中國科技博覽, 2009(34): 194-195.

[3]SILVERD,HUANGAjia,MADDISONCJ,etal.MasteringthegameofGowithdeepneuralnetworksandtreesearch[J].Nature, 2016, 529(7587): 484-489.

[4]BENCH-CAPONTJM,DUNNEPE.Argumentationinartificialintelligence[J].Artificialintelligence, 2007, 171(10/15): 619-641.

[5]PENNISIE.Breakthroughoftheyear:humangeneticvariation[J].Science, 2007, 318(5858): 1842-1843.

[6]SHANNONCE.Programmingacomputerforplayingchess[J].Philosophicalmagazine, 1950, 41(314): 2562275.

[7]BERNSTEINA,ARBUCKLET,DEVROBERTSM,etal.AchessplayingprogramfortheIBM704[C]//ProceedingsoftheMay6-8, 1958,WesternJointComputerConference:ContrastsinComputers.NewYork,NY,USA:ACM, 1958: 157-159.

[8]SAMUELAL.Somestudiesinmachinelearningusingthegameofcheckers.II:recentprogress[J].IBMjournalofresearchanddevelopment, 1967, 11(6): 601-617.

[9]FULLERSH,GASCHNIGJG,GILLOGLYJJ.Analysisofthealpha-betapruningalgorithm[R].Carnegie:CarnegieMellonUniversity, 1973.

[10]KORFRE.Depth-firstiterative-deepening:anoptimaladmissibletreesearch[J].Artificialintelligence, 1985, 27(1): 97-109.

[11]ROIZENI,PEARLJ.Aminimaxalgorithmbetterthanalpha-beta?YesandNo[J].Artificialintelligence, 1983, 21(1/2): 199-220.

[12]RUMELHARTDE,HINTONGE,WILLIAMSRJ.Learningrepresentationsbyback-propagatingerrors[J].Nature, 1986, 323(6088): 533-536.

[13]GELLYS,SILVERD.CombiningonlineandofflineknowledgeinUCT[C]//Proceedingsofthe24thInternationalConferenceonMachineLearning.NewYork,USA:ACM, 2007: 273-280.

[14]李之棠, 陳華民. 博弈樹并行搜索算法[J]. 小型微型計算機系統, 1998, 19(10): 53-56.LIZhitang,CHENHuamin.Parallelgame-treesearch[J].Mini-microsystems, 1998, 19(10): 53-56.

[15]DAVID-TABIBIO,KOPPELM,NETANYAHUNS.Geneticalgorithmsforautomaticsearchtuning[J].ICGAjournal, 2010, 33(2): 67-79.

[16]HINTONGE,SALAKHUTDINOVRR.Reducingthedimensionalityofdatawithneuralnetworks[J].Science, 2006, 313(5786): 504-507.

[17]WUIC,CHANGHC.Threat-basedproofsearchforConnect6[R].Taiwan,China:NationalChiaoTungUniversity, 2006.

[18]徐心和, 王驕. 中國象棋計算機博弈關鍵技術分析[J]. 小型微型計算機系統, 2006, 27(6): 961-969.XUXinhe,WANGJiao.KeytechnologiesanalysisofChinesechesscomputergame[J].Mini-microsystems, 2006, 27(6): 961-969.

[19]王驕, 王濤, 羅艷紅, 等. 中國象棋計算機博弈系統評估函數的自適應遺傳算法實現[J]. 東北大學學報: 自然科學版, 2005, 26(10): 949-952.WANGJiao,WANGTao,LUOYanhong,etal.ImplementationofadaptivegeneticalgorithmofevaluationfunctioninChinesechesscomputergamesystem[J].Journalofnortheasternuniversity:naturalscience, 2005, 26(10): 949-952.

[20]魏欽剛, 王驕, 徐心和, 等. 中國象棋計算機博弈開局庫研究與設計[J]. 智能系統學報, 2007, 2(1): 85-89.WEIQingang,WANGJiao,XUXinhe,etal.Astudyanddesignofopening-bookofcomputerChineseChess[J].CAAItransactionsonintelligentsystems, 2007, 2(1): 85-89.

[21]徐長明, 南曉斐, 王驕, 等. 中國象棋機器博弈的時間自適應分配策略研究[J]. 智能系統學報, 2006, 1(2): 39-43.XUChangming,NANXiaofei,WANGJiao,etal.AdaptivetimeallocationstrategyincomputergameofChineseChess[J].CAAItransactionsonintelligentsystems, 2006, 1(2): 39-43.

[22]LIUZhiqing,DOUQing.AutomaticpatternacquisitionfromgamerecordsinGO[J].ThejournalofChinauniversitiesofpostsandtelecommunications, 2007, 14(1): 100-105.

[23]LIUZhiqing,DOUQing,LIWenhong,etal.AutomaticacquisitionofpatterncollocationsinGO[J].ThejournalofChinauniversitiesofpostsandtelecommunications, 2008, 15(1): 61-67.

[24]馬驍, 王軒, 王曉龍. 一類非完備信息博弈的信息模型[J]. 計算機研究與發展, 2010, 47(12): 2100-2109.MAXiao,WANGXuan,WANGXiaolong.Theinformationmodelforaclassofimperfectinformationgame[J].Journalofcomputerresearchanddevelopment, 2010, 47(12): 2100-2109.

[25]ZHANGJiajia,WANGXuan,LINJing,etal.UCTalgorithminimperfectinformationmulti-playermilitarychessgame[C]//Proceedingsofthe11thJointConferenceonInformationSciences.AtlantisPress, 2008: 1-9.

[26]WANGX,XUZhaoyang,MAX.TD(Λ)optimizationofimperfectinformationgame’sevaluationfunction[R].Japan:WCCGC, 2007.

[27]XIAZhengyou,ZHUYongping,LUHui.UsingtheloopybeliefpropagationinSiguo[J].ICGAjournal, 2007, 30(4): 209-220.

[28]XIAZhengyou,ZHUYongping,LUHui.Evaluationfunctionforsiguogamebasedontwoattitudes[C]//ProceedingsoftheThirdInternationalConferenceonFuzzySystemsandKnowledgeDiscovery.BerlinHeidelberg:Springer, 2006: 1322-1331.

[29]BENGIOY,LAMBLINP,POPOVICID,etal.Greedylayer-wisetrainingofdeepnetworks[M]//SCH?LKOPFB,PLATTJ,HOFMANNT.AdvancesinNeuralInformationProcessingSystems,vol19.Cambridge:MITPress, 2007: 153-160.

[30]COULOMR.Computing“Eloratings”ofmovepatternsinthegameofgo[J].ICGAjournal, 2007, 30(4): 198-208.

[31]FERREIRADR.Determiningthestrengthofchessplayersbasedonactualplay[J].ICGAjournal, 2012, 35(1): 3-19.

[32]NIJSSENJAM,WINANDSMHM.Searchpoliciesinmulti-playergames1[J].ICGAjournal, 2013, 36(1): 3-21.

[33]LEIFKERDB,KANALLN.AhybridSSS*/Alpha-Betaalgorithmforparallelsearchofgametrees[C]//Proceedingsofthe9thInternationalJointConferenceonArtificialIntelligence.SanFrancisco,CA,USA:ACM, 1985, 2: 1044-1046.

[34]PLAATA,SCHAEFFERJ,PIJLSW,etal.Best-firstfixed-depthgame-treesearchinpractice[C]//Proceedingsofthe14thInternationalJointConferenceonArtificialIntelligence.SanFrancisco,CA,USA:ACM, 1995, 1: 273-279.

[35]BURNSE,LEMONSS,ZHOURong,etal.Best-firstheuristicsearchformulti-coremachines[C]//Proceedingsofthe21stInternationalJontConferenceonArtificalIntelligence.SanFrancisco,CA,USA:ACM, 2009: 449-455.

[36]王驕, 徐心和. 計算機博弈: 人工智能的前沿領域——全國大學生計算機博弈大賽[J]. 計算機教育, 2012(7): 14-18.

[37]邱虹坤. 全國計算機博弈大賽網站[EB/OL]. [2016-04-22]. 2013.http://www.caaigames.net.

[38]張利群. 實現蘇拉卡爾塔棋網絡博弈平臺的吃子算法[J]. 計算機工程與應用, 2016, 52(7): 62-66.ZHANGLiqun.RealizationofcapturealgorithmaboutSurakartachessnetworkbattleplatformincomputergame[J].Computerengineeringandapplications, 2016, 52(7): 62-66.

[39]張小川, 陳光年, 張世強, 等. 六子棋博弈的評估函數[J]. 重慶理工大學學報: 自然科學版, 2010, 24(2): 64-68.ZHANGXiaochuan,CHENGuangnian,ZHANGShiqiang,etal.Researchonevaluationfunctionsforcomputergameofconnect6[J].JournalofChongqinguniversityoftechnology:naturalscience, 2010, 24(2): 64-68.

[40]李淑琴, 李靜波, 韓裕華, 等. 蘇拉卡爾塔博弈系統中評估函數的研究[J]. 北京信息科技大學學報, 2012, 27(6): 42-45, 61.LIShuqin,LIJingbo,HANYuhua,etal.TheassessmentfunctionintheSurakartagamesystem[J].JournalofBeijinginformationscienceandtechnologyuniversity, 2012, 27(6): 42-45, 61.

[41]TANGPingzhong,LINFangzhen.Discoveringtheoremsingametheory:two-persongameswithuniquepureNashequilibriumpayoffs[J].Artificialintelligence, 2011, 175(14/15): 2010-2020.

[42]RUBINJ,WATSONI.Case-basedstrategiesincomputerpoker[J].AIcommunications, 2012, 25(1): 19-48.

[43]FLESCHJ,KUIPERSJ,SCHOENMAKERSG,etal.Subgame-perfectioninfreetransitiongames[J].Europeanjournalofoperationalresearch, 2013, 228(1): 201-207.

[44]GILPINA,SANDHOLMT.Losslessabstractionofimperfectinformationgames[J].JournaloftheACM, 2007, 54(5): 25.

[45]何大華, 陳傳波. 關于橋牌的取勝策略[J]. 華中科技大學學報: 自然科學版, 2004, 32(7): 13-15.HEDahua,CHENChuanbo.Thestrategyforwinningbridgegame[J].JournalofHuazhonguniversityofscience&technology:naturescienceedition, 2004, 32(7): 13-15.

[46]CHENBonian,LIUPangfeng,HSUSC,etal.AggregatingconsistentendgameknowledgeinChineseChess[J].Knowledge-basedsystems, 2012, 34: 34-42.

[47]郭琴琴, 李淑琴, 包華. 亞馬遜棋機器博弈系統中評估函數的研究[J]. 計算機工程與應用, 2012, 48(34): 50-54.GUOQinqin,LIShuqin,BAOHua.ResearchonevaluationfunctioncomputergameofAmazon[J].Computerengineeringandapplications, 2012, 48(34): 50-54.

[48]SCHADDMPD,WINANDSMHM.Bestreplysearchformultiplayergames[J].IEEEtransactionsoncomputationalintelligenceandAIingames, 2011, 3(1): 57-66.

[49]李學俊, 王小龍, 吳蕾, 等. 六子棋中基于局部“路”掃描方式的博弈樹生成算法[J]. 智能系統學報, 2015, 10(2): 267-272.LIXuejun,WANGXiaolong,WULei,etal.Gametreegenerationalgorithmbasedonlocal-roadscanningmethodforconnect6[J].CAAItransactionsonintelligentsystems, 2015, 10(2): 267-272.

[50]ETESSAMIK,LOCHBIHLERA.Thecomputationalcomplexityofevolutionarilystablestrategies[J].Internationaljournalofgametheory, 2008, 37(1): 93-113.

[51]高強, 徐心和. 時間復雜性和空間復雜性研究[J]. 智能系統學報, 2014, 9(5): 529-535.GAOQiang,XUXinhe.Researchontimecomplexityandspacecomplexity[J].CAAItransactionsonintelligentsystems, 2014, 9(5): 529-535.

[52]GAOQiang,XUXinhe.ResearchonthecomputationalcomplexityofnxnChinesechess[J].ICGAjournal, 2015, 38(1): 47-53.

[53]VANDERHERIKHJ,UITERWIJKJWHM,VANRIJSWIJCKJ.Gamessolved:nowandinthefuture[J].Artificialintelligence, 2002, 134(1/2): 277-311.

[54]KAINDLH,SHAMSR,HORACEKH.Minimaxsearchalgorithmswithandwithoutaspirationwindows[J].IEEEtransactionsonpatternanalysisandmachineintelligence, 1991, 13(12): 1225-1235.

[55]LUHui,XIAZhengyou.AWT:aspirationwithtimersearchalgorithminSiguo[C]//Proceedingsofthe6thInternationalConferenceonComputersandGames.BerlinHeidelberg:Springer-Verlag, 2008: 264-274.

[56]鄒競. 基于MTD(f)的中國象棋人機博弈算法的設計與優化[J]. 計算機與數字工程, 2008, 36(9): 38-43.ZOUJing.ChinesechessalgorithmdesignandoptimizebasedonMTD(f)[J].Computer&digitalengineering, 2008, 36(9): 38-43.

[57]張明亮, 李凡長. 一種新的博弈樹搜索方法[J]. 山東大學學報: 工學版, 2009, 39(6): 1-8.ZHANGMingliang,LIFanzhang.Anewsearchmethodforagametree[J].JournalofShandonguniversity:engineeringscience, 2009, 39(6): 1-8.

[58]焦尚彬, 劉丁. 博弈樹置換表啟發式算法研究[J]. 計算機工程與應用, 2010, 46(6): 42-45.JIAOShangbin,LIUDing.Researchontranslationtableheuristicalgorithm[J].Computerengineeringandapplications, 2010, 46(6): 42-45.

[59]DONKERSHHLM,UITERWIJKJWHM,VANDERHERIKHJ.Probabilisticopponent-modelsearch[J].Informationsciences, 2001, 135(3/4): 123-149.

[60]SCHAEFFERJ.TheHistoryheuristicandalpha-betasearchenhancementsinpractice[J].IEEEtransactionsonpatternanalysisandmachineintelligence, 1989, 11(11): 1203-1212.

[61]SAKUTAM,HASHIMOTOT,NAGASHIMAJ,etal.Applicationofthekiller-treeheuristicandthelambda-searchmethodtolinesofaction[J].Informationsciences, 2003, 154(3/4): 141-155.

[62]REINEFELDA,MARSLANDTA.Enhancediterative-deepeningsearch[J].IEEEtransactionsonpatternanalysisandmachineintelligence, 1994, 16(7): 701-710.

[63]MARSLANDTA,REINEFELDA,SCHAEFFERJ.LowoverheadalternativestoSSS[J].Artificialintelligence, 1987, 31(2): 185-199.

[64]PLAATA,SCHAEFFERJ,PIJLSW,etal.SSS*=alpha-beta+TT[J].ComputerScience, 2014, 8(1): 25.

[65]BERLINERH.TheB*treesearchalgorithm:abest-firstproofprocedure[J].Artificialintelligence, 1979, 12(1): 23-40.

[66]BERLINERHJ,MCCONNELLC.B*probabilitybasedsearch[J].Artificialintelligence, 1996, 86(1): 97-156.

[67]LORENTZR.UsingevaluationfunctionsinMonte-Carlotreesearch[J].Theoreticalcomputerscience, 2016, 644: 106-113.

[68]GUEZA,SILVERD,DAYANP.ScalableandefficientBayes-adaptivereinforcementlearningbasedonMonte-Carlotreesearch[J].Journalofartificialintelligenceresearch, 2013, 48(1): 841-883.

[69]BROWNECB,POWLEYE,WHITEHOUSED,etal.AsurveyofMonteCarlotreesearchmethods[J].IEEEtransactionsoncomputationalintelligenceandAIingames, 2012, 4(1): 1-43.

[70]BAIERH,WINANDSMHM.TimemanagementforMonteCarlotreesearch[J].IEEEtransactionsoncomputationalintelligenceandAIingames, 2016, 8(3): 301-314.

[71]RAIKOT,PELTONENJ.ApplicationofUCTsearchtotheconnectiongamesofHex,Y,*Star,andRenkula[C]//ProceedingsoftheFinnishAIConference.Espoo,Finland, 2008.

[72]呂艷輝, 宮瑞敏. 計算機博弈中估值算法與博弈訓練的研究[J]. 計算機工程, 2012, 38(11): 163-166.LVYanhui,GONGRuimin.Studyonvaluationalgorithmandgametrainingincomputergame[J].Computerengineering, 2012, 38(11): 163-166.

[73]TAKEUCHIS,KANEKOT,YAMAGUCHIK.EvaluationofgameTreesearchmethodsbygamerecords[J].IEEEtransactionsoncomputationalintelligenceandAIingames, 2010, 2(4): 288-302.

[74]LIEBERUMJ.Anevaluationfunctionforthegameofamazons[J].Theoreticalcomputerscience, 2005, 349(2): 230-244.

[75]MARSLANDTA,CAMPBELLM.Parallelsearchofstronglyorderedgametrees[J].ACMcomputingsurveys, 1982, 14(4): 533-551.

[76]劉建偉, 劉媛, 羅雄麟. 深度學習研究進展[J]. 計算機應用研究, 2014, 31(7): 1921-1930, 1942.

LIUJianwei,LIUYuan,LUOXionglin.Researchanddevelopmentondeeplearning[J].Applicationresearchofcomputers, 2014, 31(7): 1921-1930, 1942.

[77]XIEFan,LIUZhiqing,WANGYu,etal.SystematicImprovementofMonte-CarloTreeSearchwithSelf-generatedNeural-NetworksControllers[M]//BLUMC,BATTITIR.LearningandIntelligentOptimization:LectureNotesinComputerScience.BerlinHeidelberg:Springer, 2010: 228-231.

[78]張小川, 唐艷, 梁寧寧. 采用時間差分算法的九路圍棋機器博弈系統[J]. 智能系統學報, 2012, 7(3): 278-282.ZHANGXiaochuan,TANGYan,LIANGNingning.A9×9gocomputergamesystemusingtemporaldifference[J].CAAItransactionsonintelligentsystems, 2012, 7(3): 278-282.

王亞杰，女，1968年生，教授，博士，中國人工智能學會常務理事，中國人工智能學會機器博弈專業委員會主任。主要研究方向為機器博弈、模式識別、圖像融合，發表學術論文60余篇，主持 和參與課題20余項。.

邱虹坤，男，1971年生，講師，主要研究方向為機器博弈、智能機器人與飛行器綜合設計，指導學生在全國計算機博弈大賽中多次獲得亞馬遜棋冠軍，發表學術論文20余篇。

吳燕燕，女，1989年生，碩士，主要研究方向為圖像融合、圖像處理方面的研究，發表學術論文5篇，主持或參與課題5項。

Research and development of computer games

WANG Yajie， QIU Hongkun， WU Yanyan， LI Fei， YANG Zhoufeng

(Engineering Training Center， Shenyang Aerospace University， Shenyang 110136， China)

Computer gaming is one of the most important and challenging research directions in the field of Artificial Intelligence (AI). First, this paper reviewed the development of computer games, and the competitions in China and abroad. All types of competitions provide a platform of technical verification and academic communication for the development of computer game technology. Second, the computer game system was introduced, which includes the game platform, the game tree search, the situation evaluation, the move generation, the machine learning and other technologies. The principles and features of the typically used algorithms were stated, such as the Minimax searching algorithm, the pruning searching algorithm, the Monte Carlo searching algorithm, and so on. The situation evaluation method and many optimization algorithms were also analyzed, among which, parallel computing, the genetic algorithm and the deep learning algorithm, based on a neural network, were effective methods to promote machine intelligence. Finally, the challenges of computer games were analyzed, and the development and future trends were proposed.

artificial intelligence; computer game; Monte Carlo tree search; neural networks; genetic algorithm; deep learning

10.11992/tis.201609006

http://www.cnki.net/kcms/detail/23.1538.TP.20170111.1705.030.html

2016-09-07.

航空科學基金項目(2015ZC54008)；遼寧省教育廳基金項目(L2015407).

邱虹坤.E-mail：qiuhk@sina.com.

TP391

A

1673-4785(2016)06-0788-011

王亞杰，邱虹坤，吳燕燕，等. 計算機博弈的研究與發展[J]. 智能系統學報， 2016, 11(6): 788-798.

英文引用格式：WANG Yajie， QIU Hongkun， WU Yanyan， et al. Research and development of computer games[J]. CAAI Transactions on Intelligent Systems, 2016, 11(2): 788-798.