基于ANSYS的高壓大截面電纜金具短路電動力和機械應力分析

劉航宇　劉　念　蒲麗娟　游世良　吳　昊　李　娟

(1.四川大學電氣信息學院　成都　610065

2.四川電力設計咨詢有限公司　成都　610016)

?

基于ANSYS的高壓大截面電纜金具短路電動力和機械應力分析

劉航宇1劉念1蒲麗娟1游世良2吳昊2李娟1

(1.四川大學電氣信息學院成都610065

2.四川電力設計咨詢有限公司成都610016)

摘要采用暫態短路電流計算方法和有限元法，分析了高壓大截面電纜短路電動力的計算過程，推導出高壓大截面電纜金具短路電動力的計算公式，同時考慮電纜蛇形敷設因素、導體外層介質緩沖作用及電纜位移偏轉量，引入短路電動力工頻分量(50 Hz)修正系數K1和兩倍工頻分量(100 Hz)修正系數K2對作用在電纜金具上的短路電動力進行修正。基于ANSYS建立電纜金具系統三維有限元計算模型，分別研究電纜敷設跨距和相間距對金具應力場的影響，并對雙橋子-桃鄉220 kV電纜段進行計算。由計算結果可知，在螺桿中點處產生的應力最大，即該位置最易變形或拉裂，對于220 kV電纜工程中“一”字形排列形式，電纜敷設跨距和相間距分別應滿足l≤2.7 m，0.28 m≤a≤0.30 m。

關鍵詞：大截面電纜金具短路電流電動力有限元計算

ANSYS Based Analysis on Short-Circuit Force and Mechanical Stress of Cleats for High Voltage Large Cross-Sectional Cables

LiuHangyu1LiuNian1PuLijuan1YouShiliang2WuHao2LiJuan1

(1.College of Electrical Engineering & Information TechnologySichuan University Chengdu610065China 2.Sichuan Electric Power Design & Consulting Co.LTDChengdu610016China)

AbstractBased on transient short-circuit current calculation methods and finite element method (FEM)，the calculation process of the short-circuit forces for high voltage large-sectional cables is analyzed.And the short-circuit forces calculation formula for cleats of high voltage large cross-sectional cable is gotten.Within the formula，the snake-like layout of the cable，the mediums cushion effect at the outer conductor，and the cable movement are taken into consideration.Moreover，the coefficientsK1andK2are introduced to modify the expression of the cable cleat force caused by 50 Hz and 100 Hz frequencies respectively.The 3D finite element calculation model of the cable cleat system is established based on ANSYS.Then the effect of span spacing and phase spacing on the cable cleats stress field has been studied.At the same time，the 220 kV power cable transmission line between Shuang Qiaozi and Tao Xiang has also been calculated.As can be seen from the simulation results，the maximum value of the stress is in the middle of the bolt.So it is most easy to deform or be pulled apart.The span and phase spacing should satisfy the standardl≤2.7 m，0.28 m≤a≤0.30 m separately for 220 kV power cable transmission lines which are laid in parallel.

Keywords：Large section cable，cleats，short-circuit current，electromagnetic force，FEM calculation

0引言

隨著城市工業負荷的快速增長，城市建設與線路走廊的矛盾使得截面積大于2 000 mm2的電纜正越來越多地應用于城市用電負荷中心。國外對電壓等級為20 kV及以下、且為三角形敷設的單芯電纜在短路時進行了研究。研究表明，電纜沖擊電流最大值為105 kA，如此大的沖擊電流將在三相導體間產生巨大的電動力，該電動力可能瞬間摧毀整條電纜線路。短路電動力將導致電纜內部結構發生位移，結構變化將導致電纜內部電場畸變而發生局部放電使得絕緣被擊穿。研究對電纜金具安裝最大跨距和中間捆綁帶長度做出了規定[1-4]，但對110 kV及以上電壓等級并未進行研究，同時并未提及金具參數優化問題。

電纜金具是安裝在電纜線路上，對電纜起固定和支撐作用的電纜附件設備。電纜金具固定在安裝面上，但并不依賴于電纜安裝面[5]。電網短路時，載流導體將承受非常巨大的電動力，而電纜金具使得電纜固定，從而防止在短路電流情況下電纜電動力損傷電纜，保證電網安全穩定的運行[6]。對于短路電流來說，其產生的機械應力效應遠大于熱效應[7]。因此，對高壓大截面電纜金具短路電動力機械應力的研究具有非常重要的實際意義。

本文采用暫態短路電流計算方法和有限元法，分析短路電動力的計算原理，并根據計算原理得到短路電動力計算公式。考慮電纜蛇形敷設(蛇形敷設主要是為了吸收電纜線路熱脹、冷縮量，同時可減緩短路電動力機械響應)、導體外層介質緩沖作用和短路發生后電纜位移偏轉量等因素，引入系數K1和K2系數對作用在電纜金具上的短路電動力進行修正。基于ANSYS建立了電纜金具系統三維有限元計算模型，分別研究了敷設跨距和電纜相間距對金具應力場的影響。

1暫態短路電流計算

為分析高壓大截面電纜金具短路電動力機械應力，必須找出系統中可能出現的最嚴重的短路電流。在電力系統各類短路故障中，三相短路時產生的短路電流最為嚴重。三相短路時，暫態過程中短路電流通常包括非周期分量與周期分量兩部分。周期分量被稱為穩態分量，取決于系統短路時的阻抗；非周期分量被稱為暫態分量，取決于發生短路時電源電壓相位。

以“無窮大容量”供電系統為例，當電纜三相母線發生對稱短路，則短路時認為電壓不變、短路電流周期分量不衰減而非周期分量是衰減的，且非周期分量與短路發生瞬間與電壓的相位角有關，則三相母線上短路電流為[8]

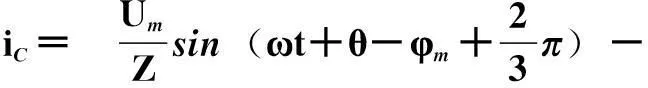
(1)

式中，Um為相電壓幅值；Z為每相回路從電源至短路點的等效短路阻抗，Z=R+jX1；ω為電源角頻率；τa為短路回路的時間常數，τa=L/R；θ為相電壓的初相位角，一般稱為合閘相角；φm為短路電流與電壓之間的相角或短路阻抗角，φm=arctan(ωL/R)。

校驗電氣設備的電動力穩定性應采用短路電流最大可能瞬時值進行計算，即短路沖擊電流，用ish表示。當電路參數已知時，短路電流周期分量的幅值是一定的，而非周期分量則按指數規律單調衰減。因此，非周期分量電流初值越大，暫態過程中短路全電流瞬時值就越大。圖1為簡單三相電路短路時的相量圖。

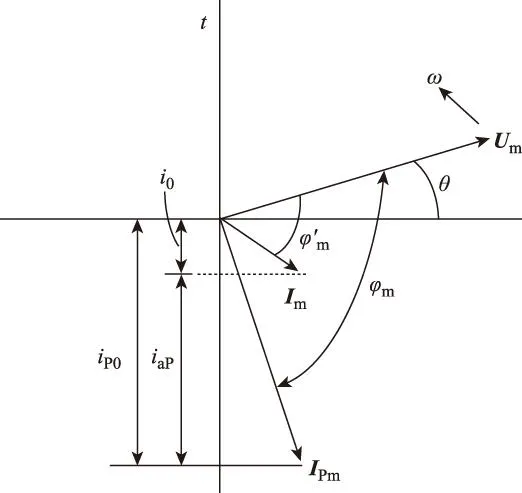
圖1　簡單三相短路相量圖Fig.1　The phasor diagram of simple three-phase short circuit

圖1中，Im、IPm分別為短路前電流幅值和短路電流周期分量的幅值，它們在時間軸t上的投影i0、 iP0分別為短路前電流和短路后周期電流的瞬時值。根據電路開閉定律，電感中的電流不能突變，因此電路中必須產生一個非周期自由電流，即非周期電流的初值為iaP。 由圖1可知，要使非周期電流有最大值，應滿足當Im-IPm在t=0時與時間軸平行。一般電力系統中，由于短路回路阻抗比電阻大得多，即ωL?R， 故可近似認為φm≈90 ℃， 即當短路前電路處于空載狀態，且短路發生時電源電動勢恰好過零，非周期電流具有最大初值。因此，短路電流的最大瞬時值在短路發生后約半個周期時出現，即t=0.01 s時，三相短路沖擊電流ish為

ish=IPm(1+e-0.01/τa)=KshIPm

Ksh=(1+e-0.01/τa)

(2)

式中，Ksh為短路電流沖擊系數，表示沖擊電流為短路電流周期分量幅值的多少倍，當時間常數由零變化到無窮大時，Ksh的取值范圍為1≤Ksh≤2。

以雙橋子-桃鄉220 kV雙回線路新建工程電纜段為例，電纜型號為YJZW02-Z 127/220 2500 mm2，線路總長1.43 km，敷設于隧道。根據該回路各參數計算得，該回路最大沖擊電流有效值為50 kA，短路時間為0.2～2 s。

2暫態短路電動力計算

圖2為電纜受力示意圖。由圖2可知，令三相電流為同向，電纜采用“一”字形排列方式，電纜任意一相導體上的電動力為中間相及另一邊緣相電纜導體中電流對其作用之和，但A、C兩相電纜導體間的距離是它們與B相電纜導體間距離的兩倍。由電動力公式可得，作用在A、B、C三相電纜導體上的電動力分別為

(3)

式中，C1、 C2、 C3表達式為

(4)

式中，(Kh)A·B， (Kh)A·C， (Kh)B·C分別為A、B，A、C和B、C相電纜導體間的回路因素；Kc為截面因素。

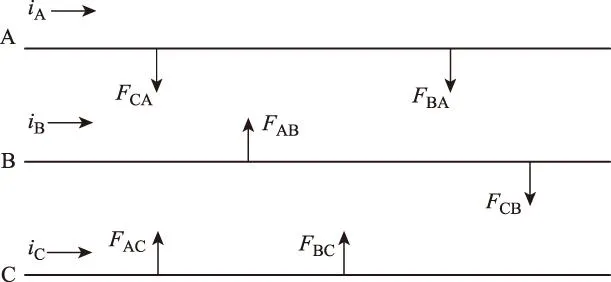
圖2　三相電纜受力示意圖Fig.2　The stress diagram of three-phase cable

因為電纜采取“一”字形對稱排列，各相電纜截面積相同，故有C1=C3=2C2， 將式(1)帶入式(3)中，其中令IPm=Um/Z， 可化簡得FA、 FB為

FB=FAB+FCB

=C1(iAiB-iBiC)

(5)

作用在A相或C相上的電動力為

FA=FBA+FCA

=C1(iAiB+0.5iAiC)

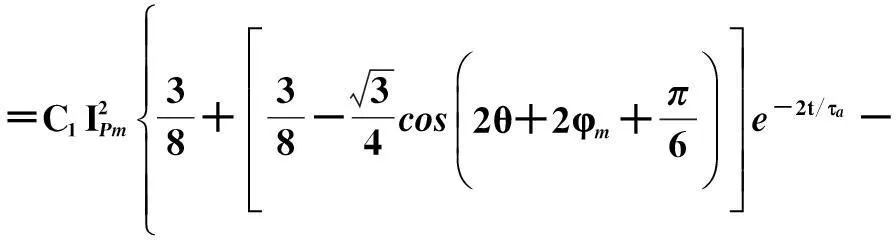
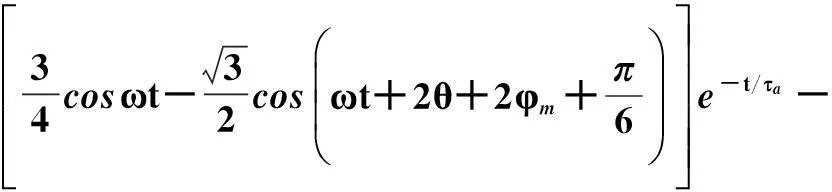
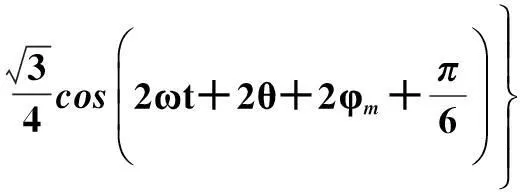
(6)

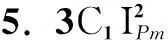
值小于采用短路沖擊電流計算所得短路沖擊電動力的值)，即在設計高壓大截面電纜金具時，金具需滿足B相載荷要求。

校核電器設備電動穩定性時，需采用短路沖擊電流峰值進行計算，當t=0.01 s時，B相短路電流瞬時值最大即短路沖擊電流，此時相短路電動力也達到最大值，短路電動力為

(7)

式中，ish為短路沖擊電流，A；l為平行導線長度或兩支撐物之間的距離，m；a為兩導體中心的距離，m；Kf為導體截面的形狀系數，對于圓形、管形導體，Kf=1.0，對其他截面導體，當l?a， Kf≈1.0。

由以上分析可知，當發生三相短路時，B相電纜所受斥力和吸力方向相反，電纜將發生振動，通過振動作用將短路電動力作用在金具上。由于交聯聚乙烯絕緣電纜內部包含內半導電包帶、導體屏蔽層、絕緣層、絕緣屏蔽層、半導電緩沖帶、波紋鋁護套以及外護套，導體外共含有7層介質，同時考慮電纜蛇形敷設以及由短路沖擊電動力產生的電纜位移偏轉量等因素[9，10]，因此，交聯聚乙烯絕緣電纜中所產生的短路電動力作用在金具機械響應緩慢，由于電纜外7層介質的緩沖作用，任何初始瞬態故障電流在導體上產生的短路電動力不可能在金具上產生同樣大小的力。圖3為 B相電纜產生的短路沖擊電動力在金具上所產生的作用力示意圖。

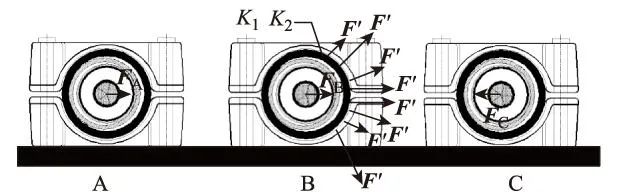
圖3　B相電纜對金具作用力示意圖Fig.3　Force diagram of the B phase cable to the cleat

圖3中標出了三相導體受力分別為FA、FB、FC。由機械振動學可知[11，12]，K1為工頻分量(50 Hz)修正系數，表達式為

(8)

K2=x′{1+(2Crf)2}1/2

(9)

式中，x′為兩倍工頻分量振幅；Cr為電纜阻尼比；f為頻率比；F′為短路電流作用在金具上的力。

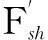
(10)

由試驗數據可知[9]，雙橋子-桃鄉220 kV雙回線路電纜隧道實際敷設跨距為l=1.5 m時，K1為0.32。由于電纜內部結構復雜使得其機械性能參數(如阻尼、自由度)難以估計，因此確定K2的值相當困難，通過試驗測試手段推薦在工程應用中K2值一般取作0.5[9，10]。

由以上參數計算可得，當t=0.01 s時，雙橋子-桃鄉220 kV的雙回線路作用在金具上的短路沖擊電動力為

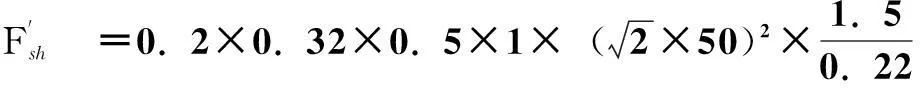
=1 090.91N

(11)

3ANSYS有限元計算模型

根據隧道敷設電纜金具安裝模型建立相應的三維有限元計算模型，雙橋子-桃鄉220 kV電纜隧道敷設如圖4所示。因為B相受力最大，所以只需對B相電纜固定和支撐金具進行研究，建立的三維有限元計算模型如圖5所示。所采用固定金具和支撐金具參數如表1和表2所示。

圖4　雙橋子-桃鄉220kV電纜隧道敷設示意圖Fig.4　The diagram for 220 kV cable transmission line called Shuang Qiaozi-Tao Xiang

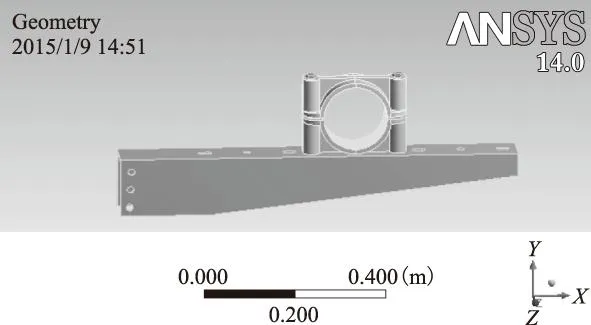
圖5　電纜固定金具及支撐金具三維模型Fig.5　3D model of power cable and cable cleat

(單位：mm)

表2　支撐金具結構參數

采用四面體單元分別對模型各部件進行自適應的網格劃分，共有20 835個單元。模型的有限元剖分結果如圖6所示。

圖6　剖分結果圖Fig.6　The meshing result

4短路電動力場計算結果及討論

根據ANSYS有限元計算模型，采用ZL2(T4及以上)鑄造鋁合金作為固定金具材料；支撐金具和螺栓材料為熱鍍鋅鋼板，材料代號為S220GD+ZF，對該電纜金具系統承受短路電動力時進行分析。短路時間為0.2～2 s，仿真計算時設置當t=0.01 s時力達到最大值，ANSYS載荷近似以線性加載。

對電纜蛇形敷設跨距和電纜相間距對電纜金具應力場的影響進行了研究。圖7、圖8分別為電纜金具整體應力分布圖和支撐金具及螺栓上的應力分布圖。

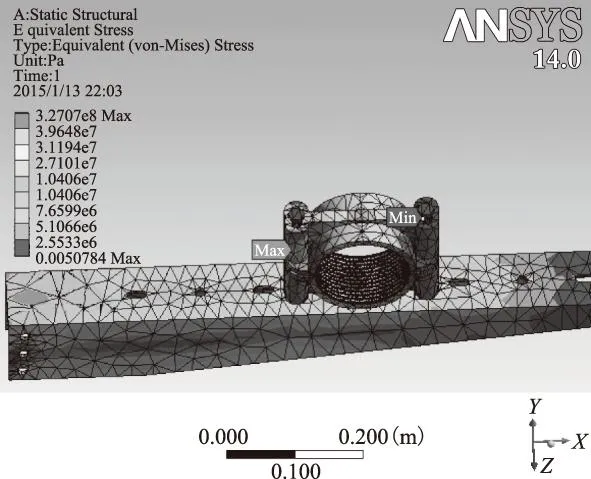
圖7　電纜金具整體應力分布圖Fig.7　The stress distribution of cable cleats.

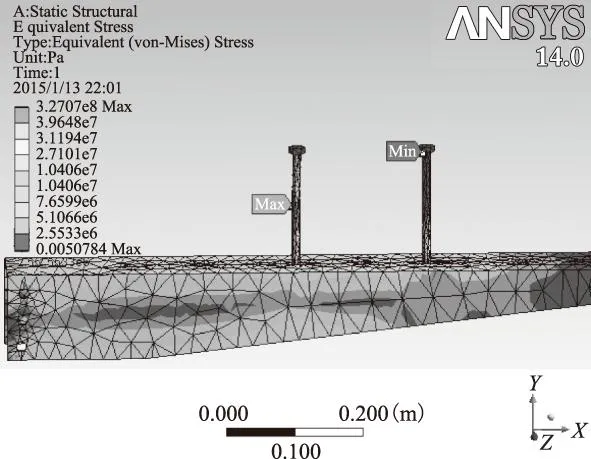
圖8　支撐金具和螺栓應力分布圖Fig.8　The stress distribution of support cleats and bolt

從圖7和圖8中可看出，固定金具在其最薄的上下壁中間所產生的應力最大，即短路電動力最易使得固定金具在上下表面變形；支撐金具在與螺栓固定處及與壁上角鋼連接處產生的應力最大，短路電動力很容易使得螺栓與支撐金具連接處螺母松動，并有可能使螺栓發生變形，固定松動很容易導致電纜損傷使得電纜系統發生故障；從圖中還可看出在螺桿中間位置所受到的應力是整個電纜金具系統最大位置，因此在考慮系統形變時應首先考慮該位置，系統中短路電動力最易導致該位置發生變形甚至拉斷。

4.1電纜蛇形敷設跨距對應力場的影響

隧道電纜蛇形敷設跨距對電纜短路電動力影響非常大。對敷設跨距l分別為1.5 m、1.8 m、2.1 m、2.4 m、2.7 m時金具應力場分布情況進行了研究，圖9為電纜隧道蛇形敷設示意圖，表3為每個跨距所對應作用在固定金具上的短路電動力。

圖9　電纜隧道蛇形敷設示意圖Fig.9　The diagram of serpentine layingin the cable tunnel

l/m1.51.82.12.42.7F'sh/N1090.911309.091527.271745.451963.63

根據GB/T 1173—1995和GB/T 2518—2008[13，14]，ZL2系列鑄造鋁合金(T4及以上)最小抗拉強度為205 MPa，電纜線芯銅導體最小抗拉強度為220 MPa，結構鋼最小抗拉強度為330 MPa。

金具應力隨跨距變化如圖10所示，隨著敷設跨距l增大，在螺栓、支撐金具及固定金具上最大應力均增大(近似為線性關系)。通過仿真計算可知，螺栓上的應力數值比支撐和固定金具上的數值高一個數量級，因此螺栓是該電纜金具系統最易發生變形或拉裂的位置，通過定性和定量的研究都證實了其與理論推導的正確性。當敷設跨距l=2.7 m時，螺栓的螺桿中間位置應力最大值為327.07 MPa，與結構鋼的最小抗拉強度330 MPa非常接近，考慮到電纜在短路電動力情況下的安全系數和強度最大要求，因此雙橋子-桃鄉220 kV的雙回線路新建工程電纜段及類似電纜工程敷設跨距應滿足l≤2.7 m。圖11為敷設跨距螺栓上產生的最大應力。

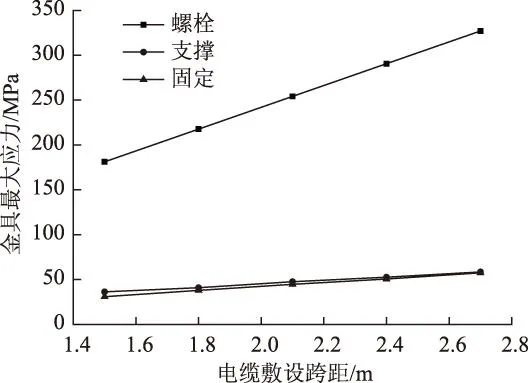
圖10　金具應力隨跨距變化圖Fig.10　Cable cleat stress changed with span spacing

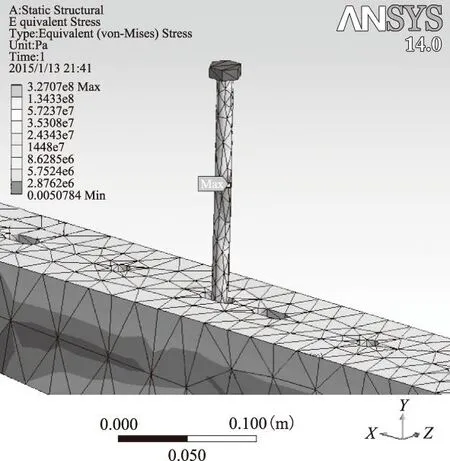
圖11　螺栓最大應力示意圖Fig.11　The maximum stress value in the bolt

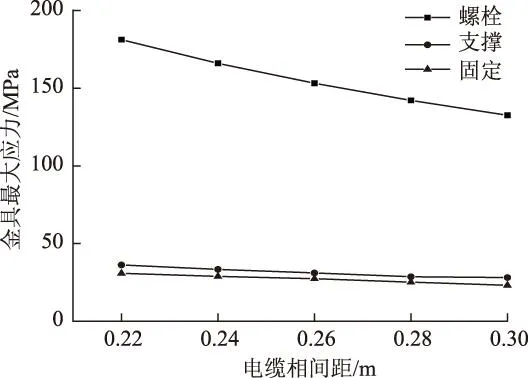
4.2電纜相間距對應力場分布的影響

電纜相間距不僅影響電纜載流量，同樣對短路電動力起著至關重要的作用。由理論分析可知，電纜相間距增大，將減弱電纜相互之間電磁感應作用，電纜損耗降低，使得電纜載流量增大且短路電動力也將減小。對于雙橋子-桃鄉220 kV的雙回線路新建工程電纜段，給出參考相間距為0.22 m，對相間距分別為0.22 m、0.24 m、0.26 m、0.28 m以及0.30 m時金具系統應力分布進行了研究。表4為相間距所對應短路電動力。

表4　不同相間距所對應短路電動力

電纜采取隧道敷設方式，由于隧道內敷設空間有限，且隧道內采取多回路敷設，因此有效利用隧道內部空間同時又不影響電纜正常運行成為當前電纜敷設中需重點研究的問題。

圖12為金具應力隨電纜相間距變化圖。由圖可知，金具應力隨著相間距增大而減小，這與理論分析相吻合。螺栓應力高于支撐和固定金具一個數量級，因此在該系統中螺栓最易變形或拉斷。考慮金具結構尺寸，仿真所得相間距對應螺栓最大應力均小于螺栓的最大應力333.15 MPa。但考慮電纜之間電磁感應和電纜散熱同載流量的關系，對于實際工程中敷設的電纜相間距建議在0.28～0.3 m。因此對于雙橋子-桃鄉220 kV的雙回線路新建工程電纜段以及類似電纜工程為“一”字形排列時，推薦電纜相間距0.28 m

圖12　金具應力隨電纜相間距變化圖Fig.12　Cable cleat stress changed with phase spacing

5結論

根據對高壓大截面電纜金具短路電流的電動力機械應力分析可得以下結論：

1)基于ANSYS仿真結果分析，螺栓螺桿中點處所產生應力值最大，其數值高于支撐和固定金具一個數量級，是該電纜金具系統中最易被短路電動力變形或拉裂位置。

2)研究了跨距對金具應力場分布的影響。通過與螺栓材料抗拉強度作比較，最后得出對于雙橋子-桃鄉220 kV的雙回線路新建工程電纜段以及類似電纜工程為“一”字形排列的敷設跨距應滿足l≤2.7 m。

3)研究了電纜相間距對金具應力場分布的影響。通過與螺栓材料抗拉強度作比較，并且考慮電纜之間電磁感應和電纜散熱與載流量關系，最后得出對于雙橋子-桃鄉220 kV的雙回線路新建工程電纜段以及類似電纜工程為“一”字形排列的電纜相間距應滿足0.28 m≤a≤0.30 m。

參考文獻

[1]Labridis D，Dokopoulos P.Finite element computation of eddy current losses in nonlinear ferromagnetic sheaths of three-phase power cables[J].IEEE Transactions on Magnetics，1994，30(4)：1407-1415.

[2]Wang X，Wang C C，Wu K.An improved optimal design scheme for high voltage cable accessories[J].IEEE Transactions on Dielectrics and Electrical Insulation，2014，21(1)：5-15.

[3]Ruger W.Mechanical short-circuit effects of single-core cables[J].IEEE Transactions on Power Delivery，1989，4(1)：68-74.

[4]BS EN 50368：Cable Cleats for Electrical Installations[S].British：European Standard，2003.

[5]Damell C A ，Bacon M L ，Shaw R A.Cable cleats-a global technique to protect three-phase single conductor cables during short-circuits[C]//Petroleum and Chemical Industry Technical Conference，Los Angeles，2004：143-150.

[6]Heinhold L.Power Cables and Their Application[M].Weinheim：Wiley-VCH，1990.

[7]Booth A W ，Hanekom A .Why correctly engineered cable cleats are vital for effective power system protection[C]//The 10th IET International Conference on Developments in Power System Protection，Manchester，2010：1-5.

[8]馮金光，王士政.發電廠電氣部分[M].北京：中國水利水電出版社，2002.

[9]Foulsham N ，Metcalfe J C ，Philbrick S E.Proposals for installation practice of single-core cables[J].Proceedings of the Institution of Electrical Engineers，1974，121(10)：1168-1174.

[10]Attri N S，Edgar J N. On the response of bus bars on elastic supports subjected to a suddenly applied force[J].IEEE Transactions on Power Delivery，1967，86(5)：636-650.

[11]金斯伯格.機械與結構振動：理論與應用[M].白化同，李俊寶，譯.北京：中國宇航出版社，2005.

[12]Den Hartog J P.Mechanical Vibrations[M].New York：McGraw-Hill，1956.

[13]GB/T 1173—1995 鑄造鋁合金[S].北京：中國標準出版社，1995.

[14]GB/T 2518—2008 連續熱鍍鋅鋼板及鋼帶[S].北京：中國標準出版社，2008.

劉航宇男，1990年生，碩士研究生，研究方向為高電壓技術與電力設備故障診斷。

E-mail：623141161@qq.com(通信作者)

劉念男，1956年生，教授，碩士研究生導師，研究方向為高電壓技術與設備故障診斷。

E-mail：liunianww@163.com

作者簡介

中圖分類號：TM757.3

收稿日期2015-01-24改稿日期2015-04-24