灰色預測GM(1,1)模型的應用及改進
吳志榮
(江蘇師范大學,江蘇 徐州 221000)
?
灰色預測GM(1,1)模型的應用及改進
吳志榮
(江蘇師范大學,江蘇 徐州 221000)
摘要:灰色GM(1,1)預測模型是灰色理論的重要組成部分,它的建立不需要有太多的樣本,不要求樣本有較好的分布規律,計算量少、有較強的適應性,所以GM(1,1)模型的應用很廣泛,本文運用GM(1,1)模型進行實例預測,最后又提出一種改進GM(1,1)模型,大大的提高了該模型對問題的預測精度。
關鍵詞:灰色預測模型;灰色理論;GM(1,1)模型
引言
20世紀80年代初,華中理工大學鄧聚龍教授首先提出了灰色系統的概念,并建立了灰色系統理論,引起了國內外很多學者、科研人員的重視。得到了深入的研究,并在眾多領域獲得了廣泛的應用。灰色系統理論在國際上也產生了很大的影響,目前在英、美、德、日等國家,有許多學者從事灰色系統的研究和應用。
1灰色GM(1,1)模型
1.1灰色預測
灰色預測是用灰色模型來進行定量分析的,通過對原始數據的生成處理尋求系統變動的規律,建立起相應的微分方程模型,預測事物未來的發展趨勢和未來狀態。
1.2GM(1,1)模型的基本原理
設x(0)=(x(0)(1),x(0)(2),…,x(0)(n))為原始數列,它的1次累加生
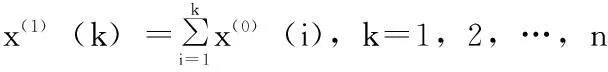
定義x(1)的灰導數為
d(k)=x(0)(k)=x(1)(k)-x(1)(k-1)
令z(1)=(z(1)(2),z(1)(3),…z(1)(n))為數列x(1)的鄰值生成數列,
其中z(1)(k)=αx(1)(k)+(1-α)x(1)(k-1)
定義GM(1,1)的灰微分方程模型為
d(k)+az(1)(k)=b
即x(0)(k)+az(1)(k)=b
其中x(0)(k)稱為灰導數,a稱為發展系數,z(1)(k)稱為白化背景值,b稱為內生控制灰數。
將時刻k=2,3,…,n代入(1)式有
引入矩陣向量記號:
數據向量參數向量數據矩陣
于是GM(1,1)模型可表示為Y=Bu.
對于GM(1,1)的灰微分方程,如果將灰導數x(0)(k)的時刻k=2,3,…,n
視為連續變量t,則x(1)視為時間t的函數x(1)(t),GM(1,1)的灰微分方程
對應的白微分方程為:
令x(1)(t=1)=x(0)(1)為初始值,
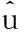
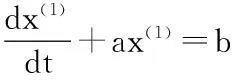
綜上所述,
得到了GM(1,1)模型的灰色預測模型為:
2實例預測
已知某食品公司2004年-2013年銷售額(見表1),在市場不會出現大的波動情況下,根據前十年的銷售額預測該公司未來10年的銷售額。
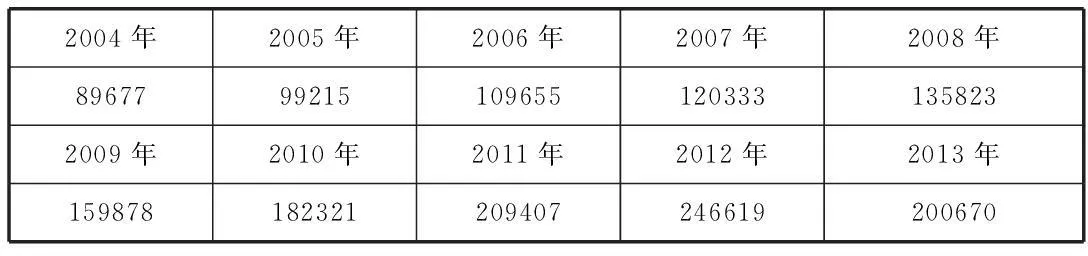
表1 單位:元
運用MATLAB編程如下:
clear
syms a b;
c=[a b]′;
A=[89677,99215,109655,120333,135823,159878,182321,209407,246619,300670];
B=cumsum(A);%原始數據累加
n=length(A);
for i=1:(n-1)
C(i)=(B(i)+B(i+1))/2;%生成累加矩陣
end
% 計算待定參數的值
D=A;D(1)=[];
D=D′;
E=[-C;ones(1,n-1)];
c=inv(E*E′)*E*D;
c=c′;
a=c(1);b=c(2);
% 預測后續數據
F=[];F(1)=A(1);
for i=2:(n+10)
F(i)=(A(1)-b/a)/exp(a*(i-1)+b/a;
end
G=[];G(1)=A(1);
For i=2:(n=10)
G(i)= F(i)- F(i-1);%得到預測出來的數據
end
編程后預測出以下:
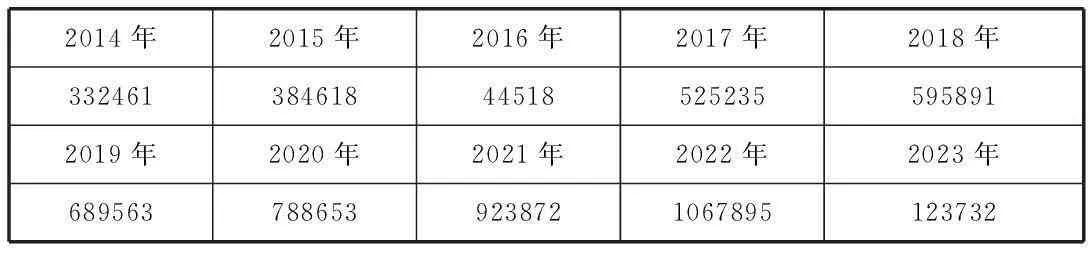
表2 單位:元
3GM(1,1)預測模型的改進
GM(1,1)模型的預測精度與可靠性主要依據原始數據的光滑度和準指數性決定。因此,如何提高原始數據的光滑度,將成為一個技術問題。
由定理如果x(0)(k)為遞增數列,并且x(0)(1)≥e,則
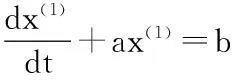
對該模型進行進一步的改進,以適應高增長序列數據.
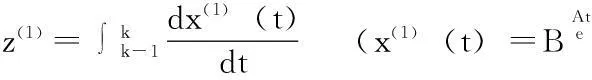
初始值最好取原始數據的最小二乘估計,即
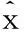
4小結
灰色預測模型是一種典型的預測方法,已經在工業、農業、經濟、社會等領域獲得廣泛應用,但同時也存在一些預測精度不高的情況。近幾年,針對這一問題很多學者對GM(1,1)模型提出了各種改進方法,來提高模型的預測的精確度。本文主要對灰色預測的實例應用,對GM(1,1)模型進一步的改進,提高模型的預測精度,將GM(1,1)進一步推廣。
參考文獻:
[1]鄧聚龍.灰色理論基礎[M]武漢:華中科技大學出版社,2002.
[2]鄧聚龍.灰色系統理論基教程[M]武漢:華中科技大學出版社,1990.
[3]李云貴,李清富,趙國藩.灰色GM(1,1)預測模型的改進[J].系統工程,1992,10(6):27-31.
[4]羅榮桂,陳煒.灰色模型的一點改進及應用[J].系統工程理論與實踐,1988(2):46-52.
[5]張大海,江世芳,史開泉.灰色預測公式的理論缺陷及改進[J].系統工程理論與實踐,2002,22-26
中圖分類號:O231
文獻標志碼:A
文章編號:1671-1602(2016)04-0235-02
作者簡介:吳志榮(1989-),女,漢族,河南南樂,研究生,江蘇師范大學,研究方向:市場營銷。

