二水平因子設(shè)計(jì)混合偏差新的下界

李洪毅，歐祖軍，黎奇升

(1.吉首大學(xué)師范學(xué)院，湖南 吉首 416000；

2.吉首大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，湖南 吉首 416000)

?

二水平因子設(shè)計(jì)混合偏差新的下界

李洪毅1，2，歐祖軍2，黎奇升2

(1.吉首大學(xué)師范學(xué)院，湖南 吉首 416000；

2.吉首大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，湖南 吉首 416000)

[摘要]混合偏差是在已有的偏差下提出的一種新的偏差，它克服了中心化L2偏差和可卷L2偏差的一些不足. 混合偏差作為部分因子設(shè)計(jì)的均勻性測度，尋找它的精確下界非常重要. 獲得了二水平設(shè)計(jì)混合偏差的一個(gè)新的下界，數(shù)值例子說明它比已有的下界在某些設(shè)計(jì)中更加精確.

[關(guān)鍵詞]U型設(shè)計(jì)；因子設(shè)計(jì)；混合偏差；下界

1預(yù)備知識

均勻設(shè)計(jì)是一種穩(wěn)健的試驗(yàn)設(shè)計(jì)，它要求試驗(yàn)點(diǎn)均勻地遍及整個(gè)設(shè)計(jì)空間.[1]偏差是用來度量試驗(yàn)點(diǎn)分布的均勻性，具有最小偏差的設(shè)計(jì)稱為在這個(gè)偏差下的均勻設(shè)計(jì).目前常用的偏差有可卷L2偏差，中心化L2偏差等.[2]但由于可卷L2偏差，中心化L2偏差在我們所研究領(lǐng)域中出現(xiàn)了一些不足，Zhou，F(xiàn)ang和Ning[3]提出了一種新的偏差即混合偏差.混合偏差作為新的均勻性測度，尋找它精確的下界是十分重要的.如果一個(gè)下界是可達(dá)的，我們就認(rèn)為這個(gè)下界是比較好的，文獻(xiàn)[3]給出了二水平因子設(shè)計(jì)在混合偏差下的一個(gè)下界.本文旨在獲得二水平部分因子設(shè)計(jì)混合偏差下的一個(gè)新的下界，且通過數(shù)值例子說明這個(gè)下界在某些設(shè)計(jì)中比已有的下界更精確.

對于一個(gè)有n次試驗(yàn)，s個(gè)q水平因子的設(shè)計(jì)，若每一列取{0，1，…，q-1}中的元素，且這q個(gè)元素出現(xiàn)的次數(shù)相等，均為n/q次，則稱該設(shè)計(jì)為U型設(shè)計(jì)，并記為U(n；qs).所有這樣設(shè)計(jì)的集合記為μ(n；qs).[4]本文主要針對二水平U型設(shè)計(jì)進(jìn)行討論.

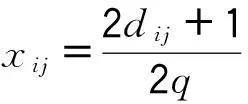
(1)

當(dāng)d∈μ(n；2s)時(shí)，(1)式可以改寫為:

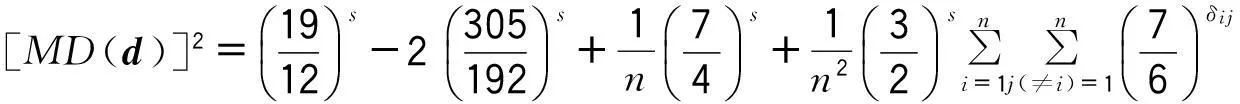
(2)

其中δij為設(shè)計(jì)d的第i行和第j行之間相應(yīng)位置上相同元素的個(gè)數(shù).

文獻(xiàn)[3]根據(jù)二水平設(shè)計(jì)d∈μ(n；2s)的混合偏差與B準(zhǔn)則的解析關(guān)系，給出了二水平因子設(shè)計(jì)的混合偏差的一個(gè)下界:

[MD(d)]2≥LMD1(d)=

(3)

其中sn，m=n(mod 2m).

引理1[5]對于任一U型設(shè)計(jì)d∈μ(n；2s)，有

證明設(shè)n×s階矩陣(α1，α2，…，αs)為設(shè)計(jì)d的設(shè)計(jì)陣，其中αk為設(shè)計(jì)d的第k列，k=1，2，…，s.由于d為U型設(shè)計(jì)，因此n是2的整數(shù)倍，即在αk中，元素0，1都出現(xiàn)n/2次，?αk，它的第i行和第j行相應(yīng)位置上的相同元素的個(gè)數(shù)記為δij(αk)，則

學(xué)生管理工作與教師自身素質(zhì)分不開，有些教師受傳統(tǒng)管理理念的影響，過分死板，忽視學(xué)生個(gè)體的發(fā)展需求，管理形式較為單一化和片面化。由于社會(huì)的進(jìn)步，學(xué)校也在不斷更新符合自身校園文化的學(xué)生管理制度，很多管理問題也隨之出現(xiàn)，導(dǎo)致有時(shí)候很多管理問題得不到充分解決，大部分流于形式，執(zhí)行不嚴(yán)，管理處于不規(guī)范、不穩(wěn)定的狀態(tài)。目前在學(xué)院“以學(xué)生為本”的全員育人環(huán)境還沒有形成，很多學(xué)院的學(xué)生管理工作者對這一事業(yè)缺乏責(zé)任心，工作不積極，更多關(guān)注自己的事業(yè)，很少把心思放在學(xué)生身上，工作者思想體制不健全，缺乏學(xué)習(xí)交流的機(jī)會(huì)，導(dǎo)致思想能力跟不上制度的要求，管理制度效果不是很理想。

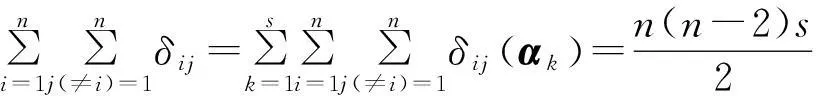
引理2[5]設(shè)l為任意正整數(shù)，d∈μ(n；2s).則

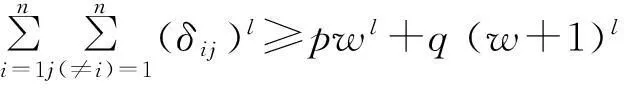
(4)

其中：w為(n-2)s/(2(n-1))的整數(shù)部分；p，q為滿足p+q=k和pw+q(w+1)=r的整數(shù)部分；k=n(n-1)；r=n(n-2)s/2.

證明設(shè)x1+x2+…+xk=r，且所有的xi都是非負(fù)整數(shù).我們只需證明

構(gòu)造Lagrange函數(shù)

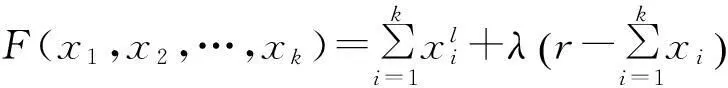
其中λ為Lagrange乘數(shù).對任意的1≤i≤k，

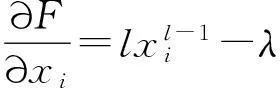
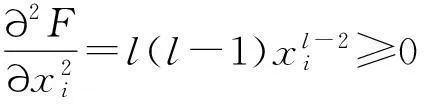
2主要結(jié)論

基于引理1和引理2，對任意的二水平U型設(shè)計(jì)d∈μ(n；2s)，我們可得到[MD(d)]2新的下界.

定理1對任意的設(shè)計(jì)d∈μ(n；2s)，有

[MD(d)]2≥LMD2(d).

其中

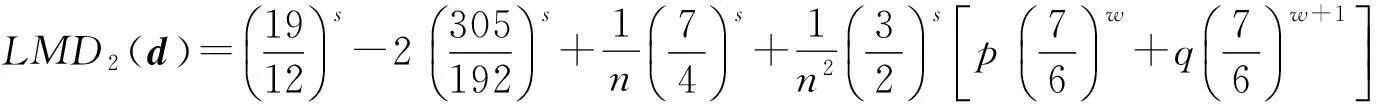
(5)

w，p和q如引理2所示.

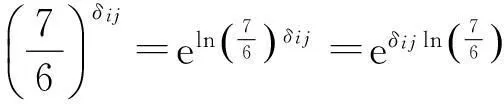
再由(4)式有

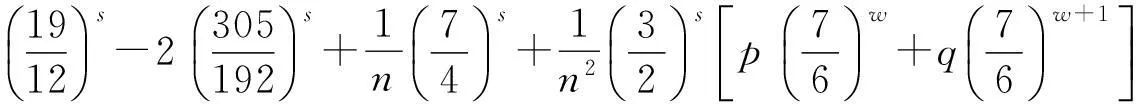
從而(5)式得證，定理證畢.

圖1　LMD2(d)與LMD1(d)的差異

下面的圖1反映了二水平因子設(shè)計(jì)混合偏差的兩個(gè)下界的差異.從圖1我們很容易發(fā)現(xiàn)有一部分LMD2(d)比LMD1(d)的值要大.

由(3)式和定理1我們可以給出任意二水平U型設(shè)計(jì)的混合偏差改進(jìn)后的下界.

定理2對任意的設(shè)計(jì)d∈μ(n；2s)，有

[MD(d)]2≥LMD(d).

其中LMD(d)=max{LMD1(d)，LMD2(d)}.

3例子

下面我們用例子來驗(yàn)證我們的結(jié)論.

例1考慮Fang和Wink[6]的三個(gè)設(shè)計(jì)d8，4∈μ(8；24)，d8，6∈μ(8；26)，d8，7∈μ(8；27)，其中n=8，s分別為4，6，7.表1分別給出了d8，4，d8，6，d8，7的設(shè)計(jì)表，混合偏差值的平方及相應(yīng)的下界.

表1　二水平設(shè)計(jì)d8,4,d8,6,d8,7的設(shè)計(jì)表，混合偏差及其下界

例2考慮Fang和Winker[6]的兩個(gè)設(shè)計(jì)d12，6∈μ(12；26)，d12，12∈μ(12；212)，其中n=12，s分別為6，12.表2分別給出了d12，6，d12，12的設(shè)計(jì)表，混合偏差值的平方及相應(yīng)的下界.

表2　二水平設(shè)計(jì)d12,6，d12,12的設(shè)計(jì)表，混合偏差值及其下界

例3考慮下面的兩個(gè)設(shè)計(jì)d6，9∈μ(6；29)，d8，10∈μ(8；210).表3分別給出了d6，9，d8，10的設(shè)計(jì)表，混合偏差值的平方及相應(yīng)的下界.

表3　二水平設(shè)計(jì)d6,9，d8,10的設(shè)計(jì)表，混合偏差值及其下界

對比表1，表2與表3的結(jié)果，我們不難發(fā)現(xiàn)：當(dāng)試驗(yàn)次數(shù)n比因子個(gè)數(shù)s大得多時(shí)，第一個(gè)下界比第二個(gè)下界好，此時(shí)LMD1(d)>LMD2(d)；當(dāng)試驗(yàn)次數(shù)n與因子個(gè)數(shù)s比較接近或相等或n

[參考文獻(xiàn)]

[1]FANG K T. Experimental design by uniform distribution[J]. Acta Mathematica Applicatae Sinica，1980，3：363-372.

[2]HICKNELL F J. A generalized discrepancy and quadrature error bound[J]. Mathematics of Computation，1998，67：299-322.

[3]ZHOU Y D，NING J H，F(xiàn)ANG K T. Mixture discrepancy for quasi-random point sets[J]. Journal of Complexity，2013，29：283-301.

[4]李華，白志東，肖玉山. 大維隨機(jī)矩陣的漸進(jìn)特征[J]. 東北師大學(xué)報(bào)(自然科學(xué)版)，2014，46(4)：1-8.

[5]CHATTERJEE K，LI Z H，QIN H. Some new lower bounds to centered and wrap-aroundL2-discrepancies[J]. Statistics and Probability Letters，2012，82：1367-1373.

[6]FANG K T，WINKER P. Lower bounds for centered and wrap-aroundL2-discrepancies and construction of uniform designs by threshold accepting[J]. Journal of Complexity，2003，19：692-711.

(責(zé)任編輯：李亞軍)

A new lower bound to mixture discrepancy in two levels fractional factorial designs

Li Hong-yi1，2， Ou Zu-jun2，Li Qi-sheng2

(1.Normal College，Jishou University，Jishou 416000，China；2.College of Mathematics and Statistics，Jishou University，Jishou 416000，China)

Abstract:The mixture discrepancy is a new discrepancy based on existing discrepancy，which overcomes some weakness of the centered and wrap-round L2-discrepancies. As the measure of uniformity of fractional factorial designs，it is very important to look for the accurate lower bounds to the mixture discrepancy.This paper gives a new lower bound to the mixture discrepancy in two levels fractional factorial designs. The new lower bound is better than existing lower bounds in certain factorials designs. Finally，some examples are given to illustrate the results.

Keywords:U type design；fractional factorial design；mixture discrepancy；lower bound

[中圖分類號]O 212.6[學(xué)科代碼]110·6745

[文獻(xiàn)標(biāo)志碼]A

[作者簡介]李洪毅(1978—)，女，博士，講師，主要從事統(tǒng)計(jì)學(xué)教學(xué)及概率統(tǒng)計(jì)研究；通訊作者：歐祖軍(1979—)，男，博士，副教授，主要從事計(jì)算機(jī)試驗(yàn)及試驗(yàn)設(shè)計(jì)研究.

[基金項(xiàng)目]國家自然科學(xué)基金資助項(xiàng)目(11201177，11561025)；湖南省教育廳優(yōu)秀青年項(xiàng)目(14B146).

[收稿日期]2014-06-23

[文章編號]1000-1832(2016)01-0034-05

[DOI]10.16163/j.cnki.22-1123/n.2016.01.009