基于遺傳算法的穩定平臺控制系統研究*
李 昂 李 楠 高 遠 郭 斌
(1.海軍駐天津地區軍事代表局 北京 100073)(2.海軍工程大學導航工程系 武漢 430033)
?
基于遺傳算法的穩定平臺控制系統研究*
李昂1李楠1高遠1郭斌2
(1.海軍駐天津地區軍事代表局北京100073)(2.海軍工程大學導航工程系武漢430033)
摘要陀螺穩定技術是重力測量領域的一項重要技術,而高精度旋轉控制是其核心技術之一。PID控制技術憑借其可靠性好、可行性強等優勢在目前的工業控制領域占有重要地位。但是傳統PID控制系統存在快速性和準確性的矛盾。為了解決陀螺穩定平臺PID控制過程中的這一矛盾,并考慮到重力測量穩定平臺的特殊控制需求,研究了一種基于遺傳算法的穩定平臺自適應控制算法。仿真實驗結果表明,相對與傳統PID控制系統,論文提出的算法具有小沖擊、動態過程好、魯棒性好等優勢。
關鍵詞重力測量; 陀螺穩定平臺; PID; 遺傳算法
Stable Platform Control System Based on Genetic Algorithm
LI Ang1LI Nan1GAO Yuan1GUO Bin2
(1. Navy Representative Bureau in Tianjin, Beijing100073)
(2. Department of Navigation, Naval University of Engineering, Wuhan430033)
AbstractGyroscope based stabilized platform is an important instrument in the field of gravity measurement. And high precision rotary control technology is one of the core technologies of stabilized platform. PID control system plays an important role in the field of industrial control for its reliability and feasibility. But, there exists a contradiction between rapidity and accuracy in the traditional PID control system. In order to compromise the contradiction in the stabilized platform system, considering the special requirements for gravity measurement stabilized platform control, a genetic algorithm based adaptive control method for the the stabilized platform is proposed in this paper. Simulation experimental results show that compared with traditional PID control system, the proposed algorithm owns the advantages of low strikes,good robustness and good dynamic process.
Key Wordsgravity measurement, stabilized platform, PID, genetic algorithm
Class NumberTP273
1引言
穩定平臺式重力儀是大地重力場測量的一種重要儀器[1~3],陀螺穩定平臺是其中必不可少的組成部分。穩定平臺的主要功能是提供高度穩定的水平基準和姿態信息,以保證重力傳感器在工作中始終保持穩定的垂直指向,消除運動載體姿態變化帶來的測量誤差,隔離振動等干擾因素對重力測量的影響。有效、可靠的控制策略是保證平臺穩定精度的的必要條件,因此對穩定平臺控制策略的研究具有重要的現實意義。
重力測量陀螺穩定平臺的工作原理如圖1所示。
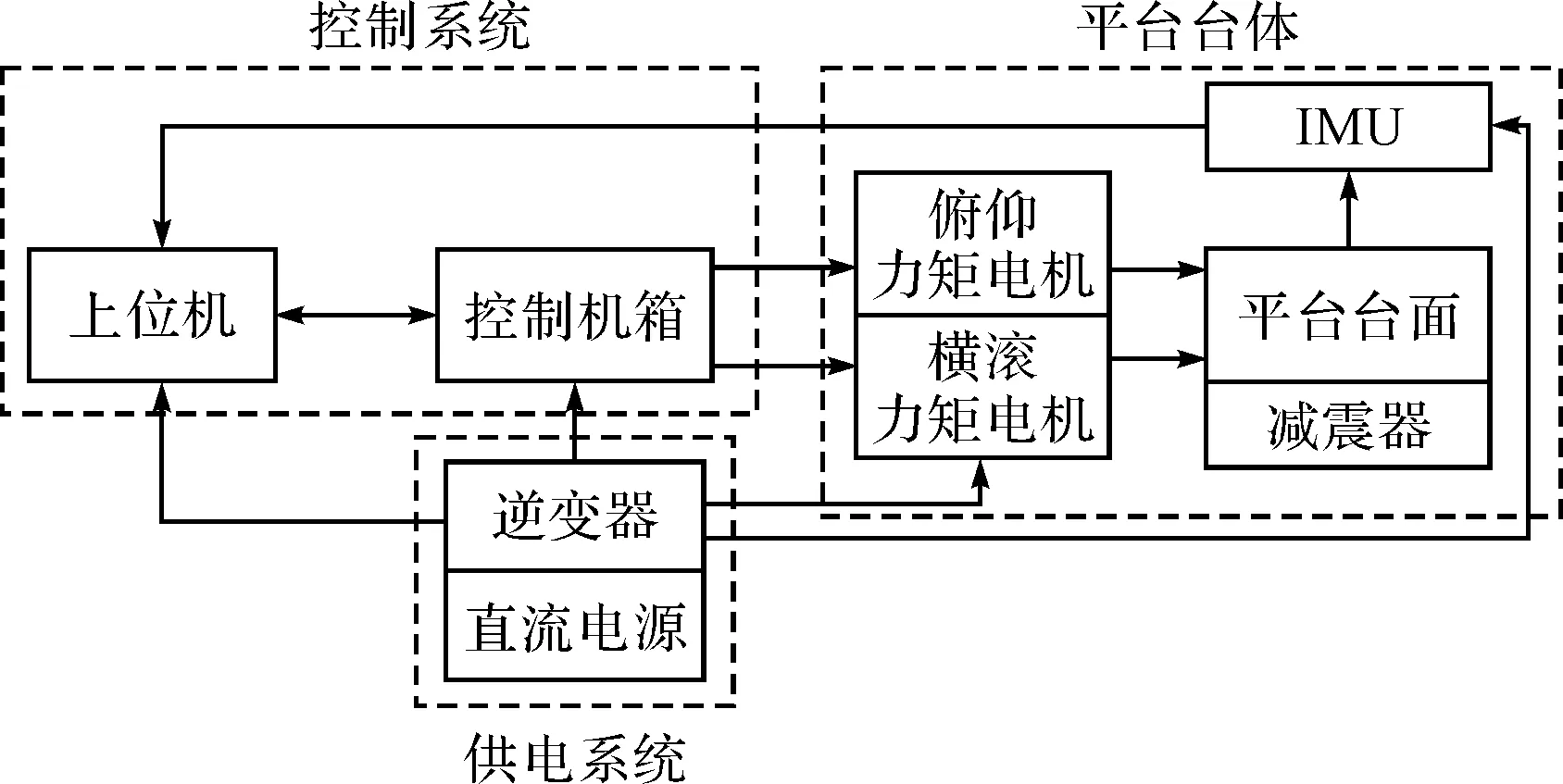
圖1 重力測量穩定平臺工作原理
與平臺臺面固連的慣性測量組件(Inertial Measurement Unit,IMU)檢測平臺的姿態、角速率等,將其傳輸給控制系統。上位機對IMU的數據進行顯示、保存,并將相關數據輸入至控制器,控制器將IMU的姿態、角速度等信號作為控制回路的輸入信號,經過解算,輸出控制信號驅動俯仰和橫滾力矩電機轉動,從而使平臺保持水平。平臺的姿態或角速率的變化又會反饋給IMU從而形成控制閉環。
在控制策略方面,PID作為一種經典的控制策略,已在工業控制中得到了廣泛應用。PID控制器目前仍是控制領域最普遍、最可靠的控制器[4~5]。但是,傳統PID控制系統存在快速性和準確性的矛盾。為了解決這一矛盾,實現穩定平臺高精度穩定控制,本文研究了一種基于遺傳算法的穩定平臺自適應控制策略。仿真研究表明,該算法能夠實現穩定平臺的平穩啟動及高精度穩定控制。
2控制系統建模
如圖1所示,本系統是兩軸兩框架結構。下面以單軸穩定系統為例,控制回路的結構如圖2所示。本系統為了保證控制精度和剛度,采用位置環和速度環的雙環控制,位置環也稱外環,速度環也稱內環。

圖2 單軸控制回路結構示意圖
根據圖2中控制系統的結構,對其進行控制系統建模。忽略電機反電勢電壓的影響,直流力矩電機的傳遞函數可以表示為
(1)
式中,Rωta為直流力矩電機的輸出扭矩,Cm為力矩電機力矩常數,La為電機電樞電感,Ra為電機電樞電阻,Uc為加在電樞兩端的電壓。
本系統中電樞電感La遠小于電樞電阻Ra。因此,本系統中,力矩電機模型可以簡化為
(2)
電機軸上的力矩平衡方程可以表示為
(3)
式中,M為電機軸上的輸入力矩,Mf為電機軸上的摩擦力矩,J為旋轉體的轉動慣量,ω為旋轉體的旋轉角速率。
上式可以同樣表示為
(4)
式中,f為電機軸上的粘滯阻力系數。
因此,旋轉體的傳遞函數可以表示為
(5)
已知系統力矩電機及旋轉體參數如下:電機力矩常數:Cm=3.292N·m/A;電樞電阻:Ra=2.65Ω;旋轉體轉動慣量為:J=1.185kg·m2;粘滯阻力系數為:f=0.00004。
于是,可得直流力矩電機的傳遞函數和旋轉體的傳遞函數分別為
(6)
(7)
因此,控制系統數學模型如圖3所示。
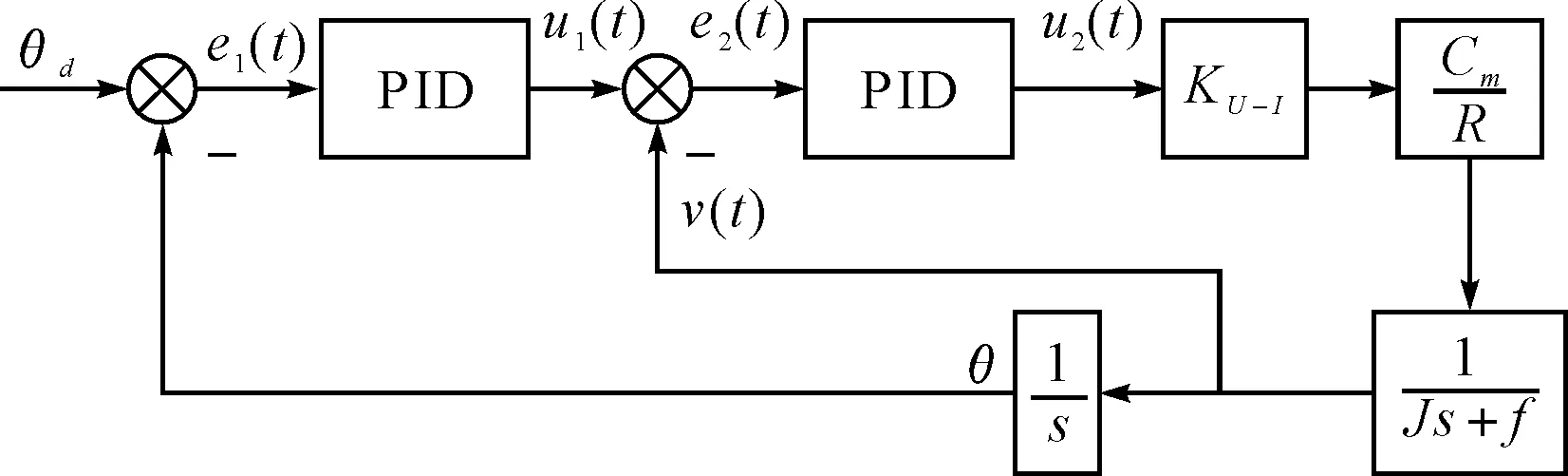
圖3 控制系統數學模型
如上圖所示,平臺穩定基準θd與IMU輸出角度θ作差得到控制位置環的控制誤差e1(t),位置環控制器輸出u1(t)與速度環輸出v(t)作差得到速度換的控制誤差e2(t),速度環控制器輸出u2(t)控制被控對象,速度環輸出v(t)經積分環節得到位置環的輸出θ。
由控制系統數學模型可以得到,被控對象的傳遞函數為
(8)
式中,KU-I為放大器的放大倍數,且KU-I=6.36。
則有:
(9)
3傳統PID算法及參數整定
PID參數整定是指通過調整PID控制器的參數,使得由控制對象、控制器等組成的控制回路的動態性能、穩態性能滿足期望的指標要求,達到理想的控制目標。目前常用的常規PID整定法有ZN經驗法、ZN臨界比例度法、特征面積法、繼電器自整定法等,其中ZN臨界比例度法是應用最為廣泛的一種整定方法。
臨界比例度法的PID控制器可表述如下
(10)
其中,δ表示比例度,e表示控制偏差,TI表示積分時間系數,TD表示微分時間系數。
調節參數的步驟如下:在閉環的情況下,系統在比例環節作用下給系統加入一個小擾動,如果系統的響應是衰減,則減小比例度,反之則增加比例度,直至閉環系統做臨界等幅周期振蕩,此時的比例度稱為臨界比例度,記為δr,其振蕩周期稱為臨界振蕩周期,記為Tr。
根據經驗公式可以確定系統的積分時間系數和微分時間系數,如表1所示。

表1 臨界比例度法PID參數
對速度環,臨界振蕩周期為Tr=0.002s。為了保證速度環的穩定性,該環中采用PI控制器。因此,由表1可得,速度環的開環傳遞函數為
(11)
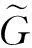
(12)
位置環的臨界振蕩周期為Tr=0.006s。由式(12)可以推出,在位置環PID控制器作用下,系統的開環傳遞函數為
(13)
其中,KP1=660.9385,KI1=220312.8442,KD1=0.5155。
利用整定得到的參數進行控制,系統對單位階躍信號的響應曲線如圖4所示。
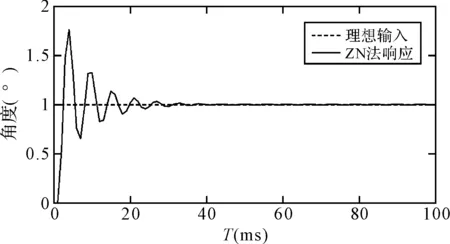
圖4 基于臨界比例度法的外環控制回路單位階躍響應
根據上述仿真結果,可以看出,傳統ZN臨界比例度參數整定方法可以整定出適當的PID參數,使系統在階躍輸入下較快地達到穩定,穩態精度高。但是為了進一步挖掘控制系統的精度潛力,從而為保證平臺穩定精度提供有力支撐,本文利用遺傳算法對PID參數進行優化,以期能夠達到更快速、更準確的控制效果。
4基于遺傳算法的自適應控制策略研究
4.1基于遺傳算法的參數整定算法
遺傳算法作為一種全局優化算法,在生產生活的各個領域得到了越來越廣泛的應用[7~10]。本文將遺傳算法與PID控制結合起來,利用遺傳算法對PID的三個系數進行整定,以得到理論上最優的PID參數。
利用遺傳算法優化KP、KI、KD的具體步驟如下:
1) 確定被控對象。式(9)描述了內環的被控對象,式(12)描述了外環的被控對象。
2) 確定每個參數的大致范圍和編碼長度,進行編碼。對KP1,KI1,KD1,KP2,KI2,KD2進行長度為20位的二進制編碼。
3) 隨機產生n個個體構成初始種群。本文使用的樣本個體數n=50。因此,初始種群是由系統隨機產生的50個60位的二進制編碼。
4) 代價函數和適配函數的確定。控制系統的優劣主要由三個方面決定,即準確性、快速性和穩定性。為了消除控制量與響應之間的誤差,將誤差量作為約束條件的一項;為了保證控制系統良好的動態性能,需要調節時間盡可能短,因此將調節時間作為約束條件的一項;過短的調節時間可能導致控制量很大,實際系統中可能導致系統失穩,因此將控制量作為約束條件的一項。基于此,將系統代價函數定義如下
(14)
式中,e(t)為系統誤差;u(t)為控制器輸出,也就是被控對象的控制量;tu為上升時間;w1,w2,w3為權值系數。根據本系統對各個控制量、控制誤差和上升時間的要求,經過反復調試,確定權值系數的值分別為:w1=0.999,w2=0.001,w3=2。
為了避免超調,采用懲罰功能。一旦產生超調,將超調量作為代價函數的一部分,此時,代價函數的表達式為
(15)
式中,w4是權值。經過調試,確定該權值系數為:w4=100。取適配函數為f=1/J。
5) 遺傳算法的操作。遺傳算法的基本操作為:復制、交叉及變異。本文中,交叉概率取為Pc=0.9。變異概率取為Pm=0.033。
6) 重復4)、5)步直到達到規定的進化代數,本文設置的進化代數為200代。
首先,利用遺傳算法對內環PID參數進行整定。結果為:KP2=121.0525、KI2=29.9552、KD2=0。然后,利用遺傳算法整定外環PID的參數值。遺傳算法整定得到的最優參數為:KP1=639.8876、KI1=144980、KD1=1.4208。這組參數對應的PID控制器對外環被控對象的控制效果如圖5所示。
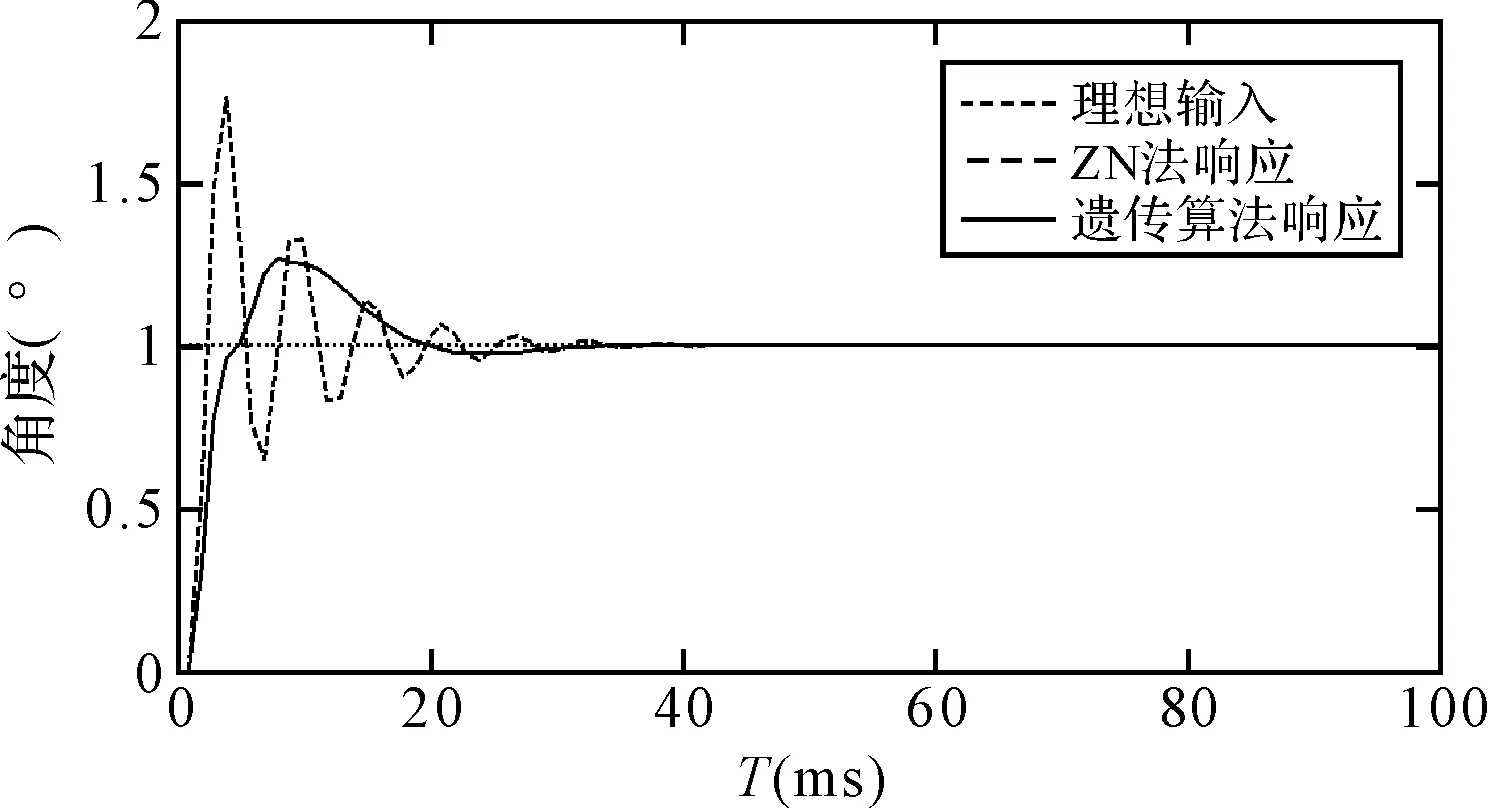
圖5 基于遺傳算法的外環控制回路單位階躍響應
如圖5所示,當給外環系統輸入一個單位階躍信號,利用遺傳算法整定出的PID參數的控制效果同樣明顯優于臨界比例度法整定出的PID參數所取得的控制效果。
4.2基于遺傳算法的自適應PID控制算法
上節中的仿真結果表明,利用遺傳算法整定出的PID參數對應的控制器的控制效果遠遠優于傳統ZN法整定出的參數所對應的控制器。其優勢主要體現在,調節時間短,動態性能好,超調量較小。這些優勢有利于在平臺產生小偏角或運動趨勢時使平臺系統快速穩定到零位,但是,當系統在大偏角下啟動或系統由于異常產生大偏角的情況下,由于控制系統的調節時間很短,平臺臺面會經歷一個劇烈調整的過程,這個過程必然會對系統產生極大的沖擊,影響重力儀、光纖IMU、電機等器件的使用壽命。如果系統采用單一參數的PID控制器,這種由控制引起的沖擊是不能避免的。基于此,本文提出了基于遺傳算法的自適應PID控制算法。根據平臺不同偏角情況下,控制系統的不同需求,建立不同的適應值函數表達式,通過遺傳算法整定出不同的PID參數,進而用不同參數的PID控制器對系統進行控制。在角度在大偏角和小偏角之間切換時,PID也相應地進行切換。
本文根據穩定平臺系統的實際需求,定義理想位置和實際位置的角度差小于或等于2°為小偏角,大于2°為大偏角。
在平臺小偏角情況下,可以使用4.1節中建立的適應值函數,通過遺傳算法來整定PID參數。這樣,可以取得較好的控制效果又不至于對系統產生過大沖擊。在大偏角情況下,則需對適應值函數進行重新設計。
因此,為了達到良好的控制效果,同樣將控制量、控制誤差和上升時間作為約束條件。與上節中建立的函數不同之處在于,在大角度下,要求調節時間在一定程度上越長越好,因此,將系統代價函數定義如下
(16)
式中,個變量的定義與上節中相同。根據本系統對各個控制量、控制誤差和上升時間的要求,經過反復調試,確定權值系數的值分別為:w1=0.0000999,w2=0.0001,w3=100。
為了避免超調,同樣采用懲罰功能,將超調量作為代價函數的一部分,此時,代價函數的表達式為
(17)
式中,w4是權值。經過調試,確定該權值系數為:w4=100。
取適配函數為f=1/J。
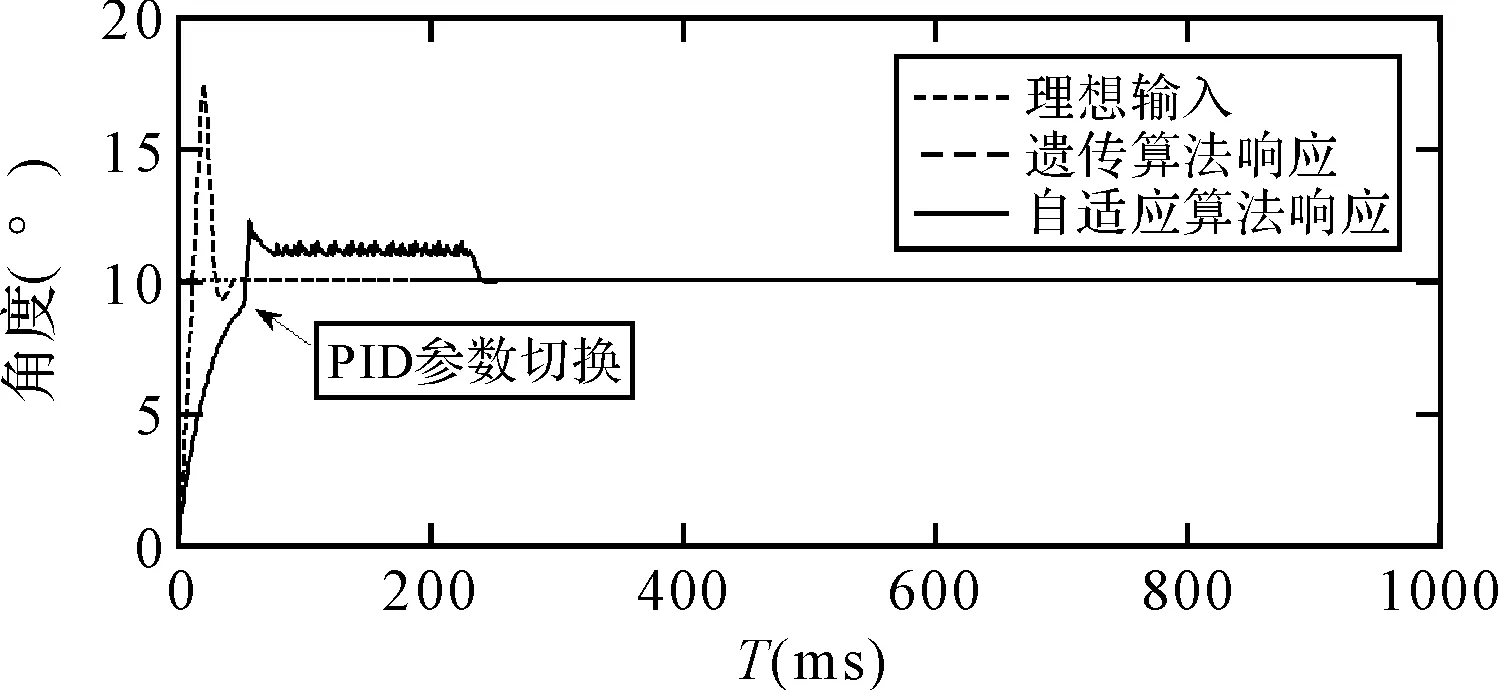
圖6 基于遺傳算法的外環控制回路單位階上躍響應
如上圖所示,當平臺處于大偏角狀態時,基于自適應算法的PID控制器與基于遺傳算法的PID控制器相比,其優勢在于: 1) 可以大大減小系統超調量; 2) 系統達到穩態之前的過渡過程時間較長。上述兩點決定了基于自適應算法的控制器使系統控制過程相對平穩、沖擊相對較小。由于PID參數的切換會引起控制回路的突變,所以在切換初期,系統會有小幅振蕩,這個不會影響系統的穩態精度。
在正常工作情況下,平臺始終處于小偏角狀態,在這一狀態下,基于遺傳算法和基于自適應算法的控制器控制效果相同。因此,基于自適應算法的控制器既能使系統具有良好的控制特性,也能在平臺大偏角啟動或異常狀態下對系統進行有效保護。
5結語
控制策略的選取直接影響重力測量穩定平臺的整體性能。針對PID控制方法中存在的快速性和有效性的矛盾難以通過傳統的參數整定方法得到有效解決的問題,本文研究了一種基于遺傳算法的自適應PID控制方法。該方法一方面實現了PID參數的快速、有效尋優,最大程度上解決快速性和準確性之間的矛盾;另一方面,又兼顧了重力測量穩定平臺的控制需求。從而能夠實現對穩定平臺的優化控制。仿真實驗表明,該算法能夠實現穩定平臺的平穩啟動、減小系統沖擊,同時能夠保證系統的穩態精度。最終作用于系統的PID參數可以保證系統有較強的魯棒性。
參 考 文 獻
[1] 吳章.CHZ海洋重力儀穩定平臺的實驗研究[D].武漢:華中科技大學,2009.
[2] 邵關.SII型海洋重力儀穩定平臺顫動故障與排除方法[J].海洋測繪,2007,27(13):78-80.
[3] 楊秀麗.陀螺穩定平臺結構分析及其優化設計[D].長春:中國科學院長春光學精密機械與物理研究所,2008.
[4] Astrom K J, Hagglund T, Hang C C, et al. Automatic tuning and adaptation for PID controllers-A survey[J]. Control Engineering Practice,1993(1):699-714.
[5] Hang C C, Ho W K, Cao L S. A comparison of two design methods for PID controllers[J]. ISATRANS,1994,33(2):147-151.
[6] 趙保才.基于遺傳算法的魯棒PID設計[D].天津:天津大學,2006.
[7] 徐磊.基于遺傳算法的多目標優化問題的研究與應用[D].長沙:中南大學,2007.
[8] 丁寅磊.基于遺傳算法的PID控制器參數優化研究[D].北京:華北電力大學,2008.
[9] 饒運清,嚴治雄,張超勇,等.一種混合遺傳算法在車間作業調度中的應用研究[J].機械科學與技術,2006,25(5):584-587.
[10] Forrest S. Genetic algorithm principles of natural selection application to computation[J]. Science,1993,26(1):872-878.
中圖分類號TP273
DOI:10.3969/j.issn.1672-9730.2016.03.012
作者簡介:李昂,男,碩士,助理工程師,研究方向:慣性技術及應用。李楠,男,工程師,研究方向:慣性技術及應用。高遠,男,研究方向:慣性技術及應用。郭斌,男,碩士研究生,研究方向:慣性技術及應用。
收稿日期:2015年9月3日,修回日期:2015年10月17日

