基于自抗擾控制器的重力穩定平臺控制系統研究*

郭　斌　許江寧　何泓洋　郭士犖

(海軍工程大學導航工程系　武漢　430033)

?

基于自抗擾控制器的重力穩定平臺控制系統研究*

郭斌許江寧何泓洋郭士犖

(海軍工程大學導航工程系武漢430033)

摘要重力穩定平臺系統是一類難以獲得精確模型的復雜非線性不確定的運動系統,由于存在機械諧振、力矩耦合負載變化及電氣參數波動等因素的影響,并且穩定平臺系統要求具有響應速度快,抗干擾能力強,穩態精度高等優良特性。但這些性能指標之間是有矛盾的。針對這一問題,設計了基于重力穩定平臺控制系統的自抗擾控制器,并進行了Simulink仿真。仿真結果表明,該系統具有很好的響應特性、自適應性和速度快,具有很高的穩態精度,而且系統對參數變化不敏感,魯棒性和抗干擾性都很強。

關鍵詞重力穩定平臺; 性能指標; 抗干擾能力; 自抗擾控制器; 控制系統

Gravity Stabilized Platform Control System Based on Active Disturbance Rejection Controller

GUO BinXU JiangningHE HongyangGUO Shiluo

(Department of Navigation, Naval University of Engineering, Wuhan430033)

AbstractGravity stabilized platform is a kind of complex uncertain movement system which is difficult to get accurate models. It can be affected by mechanical resonance, torque coupling, load change and electrical parameters fluctuations, and requires quick response speed, strong anti-jamming capability, and high steady state accuracy. However, the influences and requirements are contradictory. Therefore, an active disturbance rejection controller based on gravity stabilized platform is designed. The Simulink simulation results show that the controller possesses good response speed, adaptivity , fast speed, high steady accuracy, strong robustness and anti-interference capability and isn’t sensitive to the parameter change.

Key Wordsgravity stabilized platform, performance index, anti-jamming capability, active disturbance rejection controller, control system

Class NumberTP273

1引言

迄今為止,重力穩定平臺控制系統的設計,都是把實際系統看作線性系統,并采用線性經典控制技術進行設計。然而,隨著航天、航空、航海及現代戰爭的發展,對穩定平臺控制系統的性能指標的要求越來越高,不但要求穩定平臺控制系統具有很高的穩態精度和很好的動態品質,而且還要具有足夠大的適應范圍和抗干擾能力。因此,有必要尋找新的設計方法,改進系統的性能。近年來,國內的學者提出了慣性平臺穩定回路的變結構控制[1]及平臺穩定回路的模糊PID控制[2],并取得了較好的數值仿真結果,但是它們都顯得比較復雜。

重力穩定平臺系統是典型的運動控制,其中機械諧振、力矩耦合負載變化及電氣參數波動等因素決定了它是一類難以獲得精確模型的復雜非線性不確定系統[3]。特別是系統大部分情況下工作在低速范圍內,如何克服系統內部非線性因素(摩擦干擾、電機死區等)的影響和在一定范圍內的外部載體擾動情況下,保證伺服穩定系統具有快速的動態響應和低速運動的平穩性,是控制系統設計的難點。

自抗擾控制器(Active Disturbance Rejection Controller,ADRC)是一種不依賴于系統模型的改進型非線性PID控制器,具有低超調、收斂速度快、精度高、抗干擾能力強及算法簡單等特點,已在發電機勵磁控制、高速精加工機床控制等領域和高性能武器系統控制中得到實際應用,比傳統PID控制器更能有效抑制干擾,具有模糊控制優越的推理能力,并能在一定范圍內對非精確模型進行最佳估計。

本文提出如何用自抗擾控制技術[4]進行重力穩定平臺回路的伺服控制問題,建立穩定平臺的數學模型,并設計基于自抗擾控制器的重力穩定平臺控制系統的核心框架,詳細介紹ADRC參數整定過程,在系統模型不夠精確或者參數變化時,或者外部干擾未知的情況下,重力穩定平臺仍具有較好的穩定精度和動態響應速度,并且具有很強的抗干擾性能[5]。

2重力穩定平臺的數學模型

重力穩定平臺[6]本質上是個力矩平衡系統,干擾力矩克服摩擦力矩和電機力矩引起轉動,如圖1所示。

穩定平臺以干擾力矩M0為輸入參數,以姿態角θ為輸出參數進行建模。平臺控制器采用自抗擾控制器,其輸出控制電壓為u,功率放大器放大倍數為Kw,摩擦力矩采用庫侖-粘滯模型[7],列寫平衡方程如表1所示。

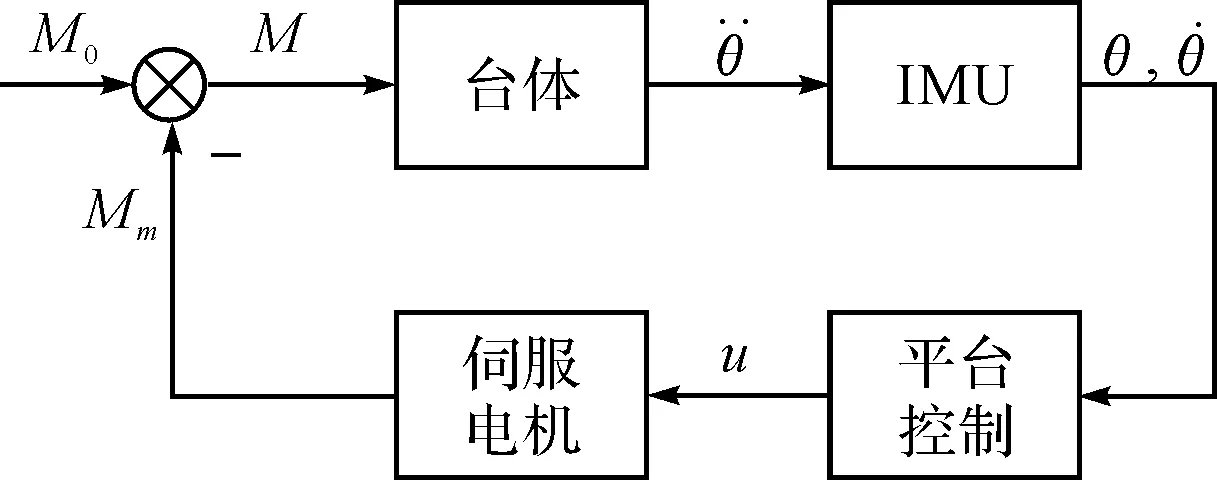
圖1　重力穩定平臺力矩平衡控制框圖

M=M0-Mf-MmM0:干擾力矩Mf:摩擦力矩Mm:力矩電機輸出力矩ω≠0Mf(t)=-(Mc+σ·ω)·sgn(ω);ω=0Mf(t)=-Mm(t),Mm(t)?Ms-Ms,Mm(t)?Ms{ω:轉子相對定子的轉動角速度σ:粘滯系數Mc:庫倫摩擦力矩Ms:靜摩擦力矩¨θ=MJ干擾力矩克服摩擦力矩和電機力矩引起轉動,確切地說應該是轉子的轉動角加速度u=ADRC(θ,θd)ADRC():ADRC控制器θ:狀態反饋θd:期望值,對于穩定平臺,≡0Ea=Kwu-CeèθMm=EaCmLaS+RaKw:功率放大倍數Ce:反電勢系數Cm:力矩系數Ra:電樞電阻La:電樞電感ω=θ-ω1ω1是定子的轉動角速度

將表中的方程式聯立,用動態結構圖表示,對應的系統控制框圖如圖2所示。

圖2　基于ADRC控制的穩定平臺控制系統框圖

對于ADRC控制系統,首先需要建立被控對象的狀態方程,以位置角作為觀測的狀態變量和輸出量,輸入為電機電壓和未知干擾,電機和平臺的狀態方程如下

(1)

3自抗擾控制器

自抗擾控制器[4]是在反饋線性化的基礎上設計的,由非線性跟蹤微分器(TD)、擴張狀態觀測器(ESO)和非線性反饋控制律(NLSEF)三部分組成。其核心是把系統的未建模動態和未知外界擾動都歸結為系統的“總擾動”而進行估計并給予補償。跟蹤微分器TD,其作用是安排過渡過程并給出此過程的微分信號;擴張狀態觀測器ESO,其作用是給由對象輸出y估計對象的狀態變量和對象總擾動的實時作用量(被控對象所有不確定模型和外擾作用的總和),這個實時估計值的補償作用使被控對象化為“積分器串聯型”;利用非線性狀態誤差反饋NLSEF對被化為“積分器串聯型”的對象進行控制。圖3為二階ADRC的原理結構框圖,圖中虛線部分為自抗擾控制器(ADRC)。

4基于自抗擾控制器的重力穩定平臺控制系統設計

基于自抗擾控制的重力儀穩定平臺單軸控制系統結構框圖如圖4所示,整個控制系統是單閉環結構,在載體干擾作用下,使平臺俯仰軸或者橫滾軸相對慣性空間的偏差角趨近于零。

圖3　二階自抗擾控制器結構框圖

根據穩定平臺的輸出和輸入關系,自抗擾控制器采用二階結構模型,由二階跟蹤微分器、三階擴張狀態觀測器和誤差反饋控制律組成。安排的過渡過程與對象狀態估計量之間誤差的適當非線性組合和未知擾動估計量的補償來生成控制信號u。

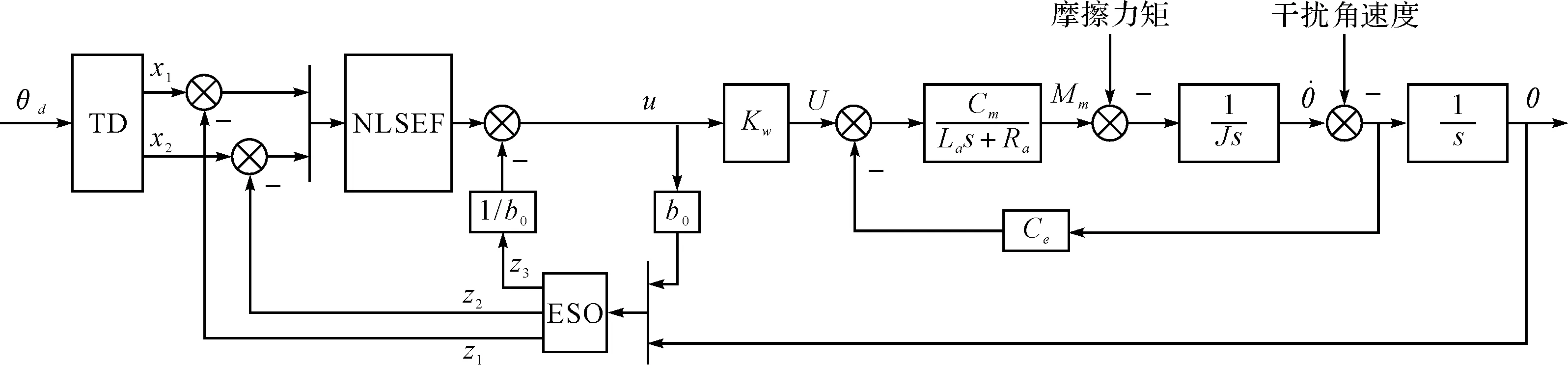
圖4　基于ADRC的重力儀穩定平臺單軸控制系統框圖

4.1ADRC算法[7]

ADRC控制器在具體實現時,為了避免高頻顫振,提高數字性能,通常采用如下離散化的控制器方程,以二階自抗擾控制器的算法歸結如下

1) 安排過渡過程(TD方程)

(2)

其中,函數fst()的定義為

d=rh,d0=dh

(3)

式中,x1和x2為狀態變量,h是數值積分的步長,濾波因子h0、速度因子r是外部可調參數。

2) 估計狀態和總擾動(ESO方程)

(4)

式中,β0i>0(i=1,2,3)。飽和函數fal(e,α,δ)的作用為抑制信號抖振,表示為

(5)

3) 誤差反饋控制律(NLSEF方程)

(6)

式中,0<α01<1<α02,e1(k)為指令信號與被控對象位置輸出之差,e2(k)為指令信號微分與被控對象速度輸出之差。

該控制器之所以稱為“自抗擾控制器(ADRC)”,就是因為ADRC把對象的“未知機理及未知干擾”都歸結為對象的未知擾動,而由對象的輸入、輸出,對它進行估計并給予補償,從而實現抗干擾功能。因此[8],ADRC并不強求對象的精確模型,只需要對象的輸入輸出數據θd、y和放大系數b0。

4.2自抗擾控制器參數整定

由ADRC算法中,y是對象的輸出,u是控制量,ADRC是由以上三部分組成,其可調參數[9]為r,h0,β01,β02,β03,α1,α2,δ,b0,β1,β2,α01,α02,δ1,δ2。

雖然ADRC的可調參數很多,但是根據TD、ESO和非線性反饋控制(NLSEF)的各自功能,可以先獨立地進行各部分的參數整定。根據經驗賦初值及參數變化規律進行參數整定:

1) TD的參數r是跟蹤微分器的速度因子,其值越大跟蹤速度越快,h0是決定濾波效果的參數。r越大,跟蹤信號越快,但噪聲放大也越厲害;h0越大,濾波效果越好,但跟蹤信號的相位也損失越大。因此r和h0需要協調調整。

2) 根據經驗取值,α1=0.5,α2=0.25。在ESO中,δ是濾波因子,δ越大,濾波效果越好,通常取值范圍5h≤δ≤10h。選擇β01,β02,β03的原則為保證ESO的穩定。一般地,β01在一定范圍內增大對系統控制品質并無較大影響,當β01增大較多時,容易引起發散振蕩,當β01減小時,系統整體的跟蹤效果變差,通常來說,β01的大小還與系統的采樣時間h有關,β01與1/h大致處于同一數量級,即β01h=1;β02的增大會產生高頻噪聲信號,導致系統控制品質惡化,β02減小會使振蕩次數增加,振蕩幅度加大;當β03增大時,系統的跟蹤速度加快,但容易引起振蕩,當β03減小時,系統的跟蹤速度減慢,過渡過程趨于平穩,不易引起振蕩,但容易引起較大的相位滯后,甚至跟蹤不上。b0比較大的話,β02和β03可以適當的取大些。

3) NLSEF參數的β1,β2相當于PD控制器的比例系數和微分增益,它們的整定也與PD控制器類似。通常,α01取為1.0、0.75、0.5,α02取1.25、1.0、0.5。δ1、δ2影響控制器的非線性性能,其值取得比較大時,ADRC可能只工作在線性區間,當其取值太小時,則容易產生顫振現象。

4) 其中b0是和系統唯一相關的參數,由表1根據系統參數計算而得,式(1)中b可為b0的參考值。參數b與被控對象有關,它代表了執行機構控制作用對系統動態特性影響的程度。實際上b不能精確已知,以b0代替b,要求b0在b附近的范圍內變化,隨著對象增益變大或時滯變大,可適當增大b0。大量仿真經驗表明,b0的取值一般在0.01~10變化。

ADRC參數多,待初值確定后,其控制性能主要由幾個參數決定,圖5為待初值確定后ADRC控制器參數整定流程[9]。

5仿真結果

根據圖2的結構框圖,構建基于S函數的穩定平臺ADRC控制仿真模型并進行仿真。

圖5　待初值確定后ADRC參數整定流程

參考上節所述的ADRC控制參數整定的經驗方法,經過仿真調試,2階跟蹤微分器(TD),非線性控制器(NLSEF)和3階擴張狀態觀測器(ESO)的各主要仿真參數設置如下:

· TD:采樣時間T=0.001s,h0=h=T,r=100;

· ESO:β01=1000,β02=3000,β03=2000,α1=0.5,α2=0.25,δ=0.05;

· NLSEF:β1=100,β2=200,α01=0.5,α02=0.25,δ1=δ2=0.05,b0=2.16。

5.1跟隨性能分析

1) 穩定精度

控制系統的穩定精度是控制器性能的一項重要指標。給定位置輸入為零,載體出現干擾時,橫滾角Rf的穩態輸出角度波形如圖6所示。

圖6　穩定平臺的穩定角度曲線

此時橫滾角的最大跟蹤誤差約為0.2mrad≈0.69′,但是由于自抗擾算法本身存在一些非線性因子在里面,所以從穩定角度曲線可以看出穩定曲線振蕩相對比較厲害,高頻成分相對較多。

2) 階躍輸入信號的跟蹤性能

在10s時,對穩定平臺系統施加10rad的階躍輸入信號,系統的階躍輸出響應如圖7所示。

圖7　階躍響應曲線

可以看出,對于階躍輸入信號,控制系統輸出無超調,而且響應速度快,調節時間約2s。在ADRC控制器中,通過跟蹤微分器(TD)的作用,有效解決了系統快速性與超調的矛盾。

3) 對干擾力矩的跟蹤

伺服控制系統既是角度跟隨系統,又是力矩平衡系統。對穩定平臺直接施加正弦干擾轉矩,電機輸出轉矩能夠實時跟蹤輸入的干擾力矩,如圖8所示。

圖8　正弦干擾轉矩時電機的輸出轉矩波形(ADRC)

圖9是系統采用傳統PID控制算法時,電機輸出力矩跟蹤干擾力矩的波形。與圖8進行對比可以看出,ADRC的跟蹤精度更高。

圖9　正弦干擾轉矩時電機的輸出轉矩波形(PID)

5.2抗干擾性能分析

當載體擾動正弦速度信號周期7秒,幅值為25°/s時,平臺隔離擾動的響應如圖10所示。

由圖10可以看出,載體擾動速度幅值為25°時,穩定平臺在慣性空間的偏差角度僅為0.01°(0.6角分),隔離效果[10]為0.04%,使穩定平臺在慣性空間保持穩定。和經典PID控制方式相比,抑制載體擾動對重力儀的影響的效果更好。

圖10　穩定平臺的載體擾動與系統輸出

就本系統而言,內擾主要由平臺系統內部參數辨識的不準確或者參數隨環境和時間變化引起的,外擾則主要由基座擾動產生的摩擦干擾力矩引起。保持ADRC控制器各參數不變,改變平臺的電氣參數,運行仿真,參數改變前后得到穩定角度如圖11所示。

圖11　轉動慣量變化時穩定平臺的穩定角度曲線

可以看出,系統的參數變化后同樣能保持較高的精度,驗證了ADRC抗內擾的特性,控制器具有較好的自適應性。

6結語

本文對基于自抗擾控制器的重力穩定平臺控制系統進行了研究,建立了重力穩定平臺的數學模型,闡述了自抗擾控制器的結構及原理,設計了基于自抗擾控制器的重力穩定平臺控制系統的核心框架,分別介紹了ADRC算法以及ADRC參數整定過程。仿真結果表明,該系統具有很好的響應特性和自適應性,無超調、響應速度快、無振蕩,具有很高的穩態精度,系統對參數變化不敏感,魯棒性和抗干擾性都很強。

參 考 文 獻

[1] 程婧容,楊慶明,談振藩.慣性平臺穩定回路的變結構控制[J].中國慣性技術學報,1999,7(4):73-76.

[2] 魏宗康,等.平臺穩定回路的模糊-PID最優控制設計[J].慣導與儀表,2000(3):1-8.

[3] Sun Liming, Jiang Xuezhi, Li Donghai. Tuning of Auto Disturbance Rejection Controller for a Class of Nonlinear Plants[J]. Acta Automatica Sinica,2004,30(2):251-254.

[4] 韓京清.自抗擾控制器及其應用[J].控制與決策,1998(1):18-23.

[5] Dong S. Comments on Active Disturbance Rejection Control[J]. IEEE Transactions on Industrial Electronics,2007,54(6):3428-3429.

[6] 許江寧,朱濤,卞鴻巍.航空攝影陀螺穩定平臺[J].儀器儀表學報,2007,28(5):914-917.

[7] 劉金琨.先進PID控制MATLAB仿真[M].第3版.北京:電子工業出版社,2013:201-239.

[8] 宋金來,楊雨,等.慣性平臺穩定回路的自抗擾控制[J].系統仿真學報,2002,14(3):391-393.

[9] 尹水紅.自抗擾技術在多變量控制系統中的應用[D].北京:華北電力大學,2007:56-59.

[10] 李賢濤,張葆,等.基于自適應的自抗擾控制技術提高擾動隔離度[J].吉林大學學報,2015,45(1):202-208.

中圖分類號TP273

DOI:10.3969/j.issn.1672-9730.2016.03.013

作者簡介:郭斌,男,碩士研究生,研究方向:慣性技術及應用。

基金項目:國家自然科學基金(編號:41404002,41574069);國家重大科學儀器開發專項(編號:2011yq12004502)資助。

收稿日期:2015年9月14日,修回日期:2015年10月28日