機(jī)抖激光陀螺敏感軸動態(tài)偏移誤差參數(shù)估計(jì)與補(bǔ)償

王 林，吳文啟，潘獻(xiàn)飛，李 耿

（1. 國防科學(xué)技術(shù)大學(xué) 機(jī)電工程與自動化學(xué)院，長沙 410073；2. 國防科學(xué)技術(shù)大學(xué) 光電科學(xué)與工程學(xué)院，長沙 410073）

機(jī)抖激光陀螺敏感軸動態(tài)偏移誤差參數(shù)估計(jì)與補(bǔ)償

王 林1，吳文啟1，潘獻(xiàn)飛1，李 耿2

（1. 國防科學(xué)技術(shù)大學(xué) 機(jī)電工程與自動化學(xué)院，長沙 410073；2. 國防科學(xué)技術(shù)大學(xué) 光電科學(xué)與工程學(xué)院，長沙 410073）

針對振動環(huán)境下機(jī)抖激光陀螺敏感軸產(chǎn)生動態(tài)偏移造成慣導(dǎo)系統(tǒng)精度下降的問題，從理論上推導(dǎo)了機(jī)抖激光陀螺敏感軸動態(tài)偏移誤差模型，并結(jié)合工程實(shí)際建立了簡化的誤差模型；在此簡化誤差模型基礎(chǔ)上，推導(dǎo)了陀螺敏感軸動態(tài)偏移造成的等效陀螺漂移與比力、角速度的耦合關(guān)系；將機(jī)抖激光陀螺敏感軸動態(tài)偏移誤差歸結(jié)為9個待辨識參數(shù)，針對該模型中的待辨識參數(shù)設(shè)計(jì)了標(biāo)定方法，并給出了標(biāo)定實(shí)驗(yàn)設(shè)計(jì)原則；以姿態(tài)誤差為觀測量進(jìn)行振動實(shí)驗(yàn)對待辨識參數(shù)進(jìn)行估計(jì)，振動實(shí)驗(yàn)結(jié)果表明，在10 min線振動時間內(nèi)，機(jī)抖激光陀螺敏感軸動態(tài)偏移誤差補(bǔ)償后，捷聯(lián)慣導(dǎo)系統(tǒng)純慣導(dǎo)速度誤差減小30%以上。

機(jī)抖激光陀螺；敏感軸動態(tài)偏移；誤差模型；參數(shù)標(biāo)定

機(jī)抖激光陀螺以其特有的優(yōu)勢在捷聯(lián)式慣性導(dǎo)航系統(tǒng)中得到了廣泛應(yīng)用。捷聯(lián)式慣性導(dǎo)航系統(tǒng)由于與載體直接固聯(lián)，慣性器件直接敏感載體的運(yùn)動，因此對慣性器件的性能提出了更高的要求。

影響捷聯(lián)式慣導(dǎo)系統(tǒng)導(dǎo)航精度的原因很多，除了安裝誤差、標(biāo)度因數(shù)誤差、慣性器件的零位誤差外，運(yùn)載體線振動、角振動造成的動態(tài)誤差也是很重要的因素。為了減小振動對機(jī)抖激光陀螺捷聯(lián)慣導(dǎo)系統(tǒng)的影響，需要合理設(shè)計(jì)減振結(jié)構(gòu)[1-4]。在充分減振的基礎(chǔ)上，振動環(huán)境下慣導(dǎo)系統(tǒng)的精度仍迅速下降，產(chǎn)生了明顯的姿態(tài)漂移，即使將姿態(tài)解算頻率提高到 4000 Hz，導(dǎo)航誤差仍然沒有得到改善。文獻(xiàn)[5]中對俄羅斯Cyclone 4運(yùn)載火箭的機(jī)抖激光陀螺捷聯(lián)慣導(dǎo)系統(tǒng)的隨機(jī)振動試驗(yàn)測試也表明，振動環(huán)境下，激光陀螺可能存在與高頻振動分量相關(guān)的誤差。由于機(jī)抖激光陀螺存在活動部件抖輪[6]，加速度作用下抖動軸彎曲，形成等效安裝偏差，進(jìn)而產(chǎn)生等效陀螺漂移。

針對這種情況，文獻(xiàn)[7-9]重新設(shè)計(jì)了機(jī)抖激光陀螺抖輪的結(jié)構(gòu)，使得單表級激光陀螺在振動環(huán)境下的精度有了明顯改善，但是沒有給出振動環(huán)境下系統(tǒng)級精度測試情況。文獻(xiàn)[10]理論推導(dǎo)了由機(jī)抖激光陀螺抖動軸彎曲變形造成的漂移誤差，認(rèn)為該誤差與輸入加速度及載體的動態(tài)頻率成正比，并進(jìn)行了仿真驗(yàn)證，但沒有進(jìn)一步的實(shí)驗(yàn)驗(yàn)證和誤差補(bǔ)償方法。目前公開的文獻(xiàn)很少有關(guān)于機(jī)抖激光陀螺敏感軸動態(tài)偏移誤差模型的解析分析及其誤差參數(shù)標(biāo)定方案。

本文建立了機(jī)抖激光陀螺敏感軸動態(tài)偏移的理論模型，分析其誤差機(jī)理，并設(shè)計(jì)了相關(guān)誤差參數(shù)的標(biāo)定方法，最后給出了初步的誤差補(bǔ)償實(shí)驗(yàn)結(jié)果。

1 機(jī)抖激光陀螺敏感軸動態(tài)偏移誤差模型

設(shè)機(jī)抖激光陀螺捷聯(lián)慣導(dǎo)系統(tǒng)IMU的x陀螺敏感軸為x軸，y陀螺敏感軸為y軸，z陀螺敏感軸為z軸；設(shè)εxy、εxz分別為x陀螺敏感軸繞y軸、z軸轉(zhuǎn)動的形變角；εyx、εyz分別為y陀螺敏感軸繞x軸、z軸轉(zhuǎn)動的形變角；εzx、εzy分別為z陀螺敏感軸繞x軸、y軸轉(zhuǎn)動的形變角。無外部力學(xué)環(huán)境作用下，以x陀螺敏感軸為基準(zhǔn)，εyz0為y陀螺敏感軸繞z軸轉(zhuǎn)動的常值偏角；εzx0、εzy0分別為z陀螺敏感軸繞x軸、y軸轉(zhuǎn)動的常值偏角，則動態(tài)情況下敏感軸動態(tài)偏移造成的等效陀螺漂移誤差模型可表示為

式中：第一項(xiàng)為陀螺敏感軸常值偏角、動態(tài)偏移形變角對應(yīng)的等效安裝偏差造成的動態(tài)誤差，第二項(xiàng)為陀螺敏感軸動態(tài)偏移形變角對應(yīng)的等效圓錐誤差。

陀螺敏感軸動態(tài)偏移形變角滿足以下動力學(xué)方程：

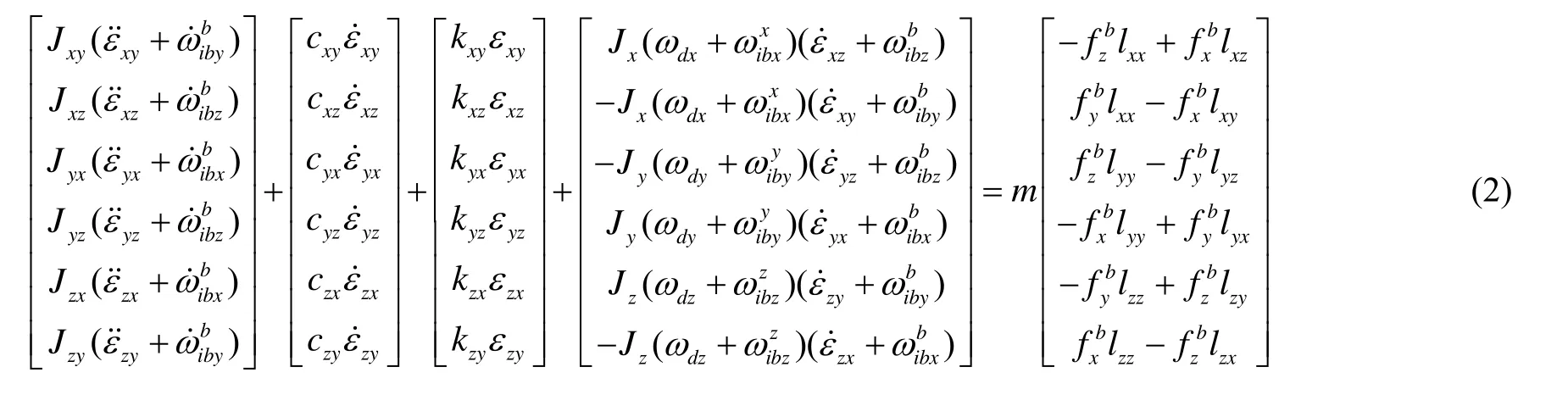
式中：Jx=Jy=Jz=J為x陀螺、y陀螺、z陀螺繞其各自敏感軸方向的轉(zhuǎn)動慣量；

Jxy≈Jxz≈Jyx≈Jyz≈Jzx≈Jzy≈J1為x陀螺、y陀螺、z陀螺繞與其敏感軸正交的對稱軸的轉(zhuǎn)動慣量；

cxy≈cxz≈cyx≈cyz≈czx≈czy≈c 為陀螺抖輪的側(cè)向形變阻尼；

kxy、kxz、kyx、kyz、kzx、kzy分別為各個陀螺抖輪的側(cè)向剛度，m為陀螺光學(xué)本體的質(zhì)量；

[lxxlxylxz]T、[lyxlyylyz]T、[lzxlzylzz]T分別為x陀螺、y陀螺、z陀螺質(zhì)心偏離的桿臂參數(shù)；

ωdx、ωdy、ωdz分別為x陀螺、y陀螺、z陀螺的抖動角速率。

同一陀螺不同方向的側(cè)向剛度非常接近，可以忽略非等彈性的影響，即：

為便于實(shí)際工程應(yīng)用，對式(2)進(jìn)行簡化，以x陀螺為例進(jìn)行說明。考慮到x陀螺沿y、z方向形變阻尼的影響，忽略交叉耦合項(xiàng)的影響，同時忽略、的影響(其影響等價于動力學(xué)方程的外界輸入)，只考慮偏心力矩對 x陀螺敏感軸側(cè)向形變的影響。x陀螺的動力學(xué)方程可以簡化為

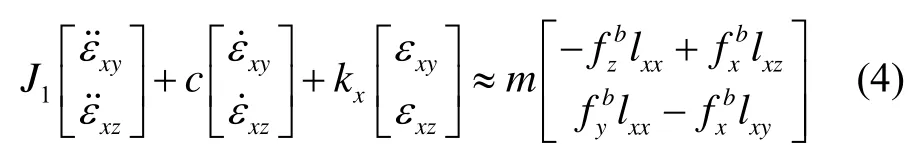
假設(shè)作用到x陀螺上的等效偏心力矩為正弦力矩Mcos(ωt)，由于減振器對高頻振動的隔離，實(shí)際作用于陀螺的偏心力矩的頻譜集中于低頻段。鑒于陀螺敏感軸側(cè)向形變的固有頻率一般在700 Hz以上[10]，則有：

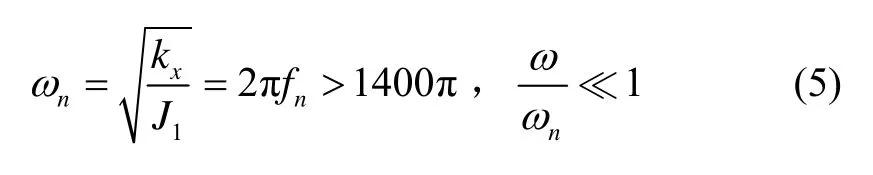
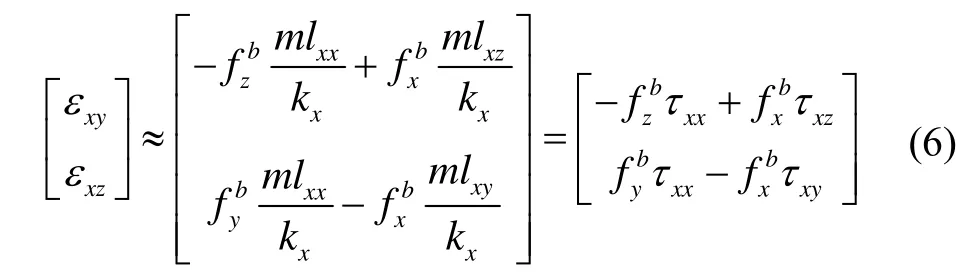
同理，可得y、z陀螺側(cè)向形變的穩(wěn)態(tài)響應(yīng)近似解。式(2)所示動力學(xué)方程的穩(wěn)態(tài)響應(yīng)近似解為

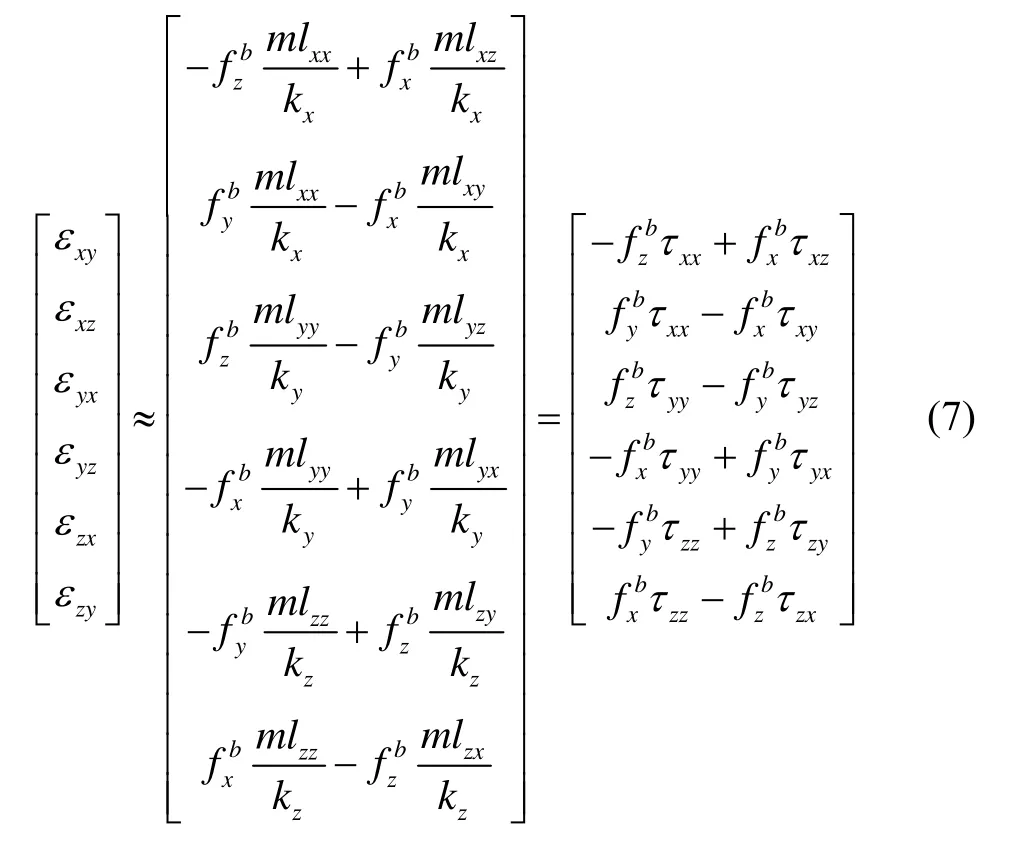
考慮到式(1)中陀螺敏感軸常值偏角是陀螺安裝參數(shù)的一部分，可以通過標(biāo)定消除。忽略非等彈性影響時，陀螺敏感軸動態(tài)偏移形變角對應(yīng)的等效圓錐誤差也很小，可以忽略。進(jìn)一步根據(jù)式(7)，將式(1)簡化為

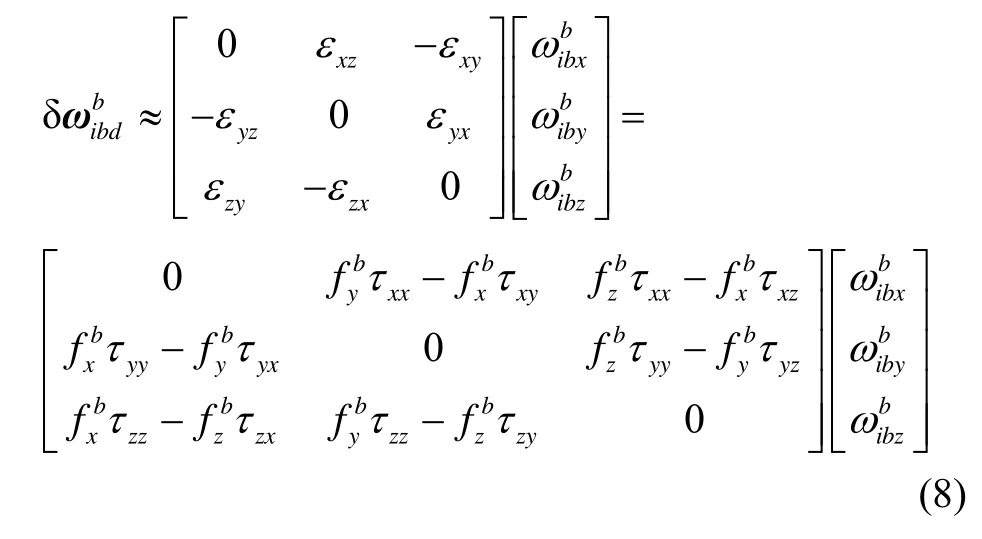
式(8)即待分析評估的結(jié)合機(jī)抖激光陀螺敏感軸偏移形變的動態(tài)誤差補(bǔ)償簡化模型，包含9個待辨識的參數(shù)。根據(jù)該式，在復(fù)雜線振動、角振動環(huán)境下，會耦合出等效陀螺漂移誤差，造成姿態(tài)誤差，進(jìn)而造成速度、位置誤差。

2 誤差參數(shù)標(biāo)定

在固定位置處，靜止一段時間后，繼而對慣導(dǎo)系統(tǒng)施以固定頻率線振動。機(jī)抖激光陀螺敏感軸偏移形變會產(chǎn)生等效陀螺漂移，相對地理系造成的姿態(tài)誤差微分方程表示為

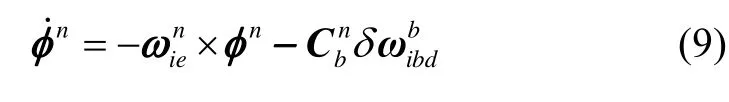
記時刻t0為線振動開始時刻，振動持續(xù)時間記為T，則t0+T時刻的姿態(tài)誤差為

考慮到式(11)右側(cè)包含φn(t)項(xiàng)，采用遞推數(shù)值積分獲得式(11)的數(shù)值解，該數(shù)值解表示為τ的函數(shù)形式。忽略對準(zhǔn)造成的姿態(tài)誤差，即時刻t0的姿態(tài)誤差記為φn(t0)=0。t0+T時刻線振動結(jié)束，慣導(dǎo)靜止一段時間進(jìn)行對準(zhǔn)，利用此姿態(tài)基準(zhǔn)獲得t+T時刻的姿態(tài)誤差觀測值：

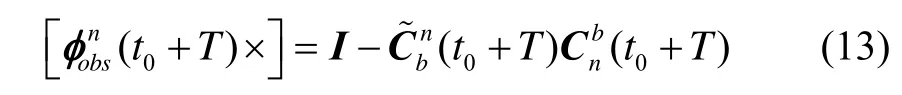
根據(jù)式(11)、(13)，設(shè)計(jì)多組線振動實(shí)驗(yàn)，利用最小二乘法實(shí)現(xiàn)九個誤差參數(shù)的標(biāo)定。

3 實(shí)驗(yàn)設(shè)計(jì)及初步的結(jié)果

標(biāo)定過程需要充分激勵誤差，不同振動實(shí)驗(yàn)條件下，可以對不同的待辨識參數(shù)造成的誤差進(jìn)行充分激勵。從式(8)可以看出，比力與角速率乘積項(xiàng)耦合，產(chǎn)生等效漂移。據(jù)此，可以設(shè)計(jì)線振動實(shí)驗(yàn)對待辨識參數(shù)進(jìn)行標(biāo)定估計(jì)。

線振動實(shí)驗(yàn)設(shè)計(jì)：為了使得慣導(dǎo)系統(tǒng)在線振動條件下同時存在較大的角運(yùn)動，需要在慣導(dǎo)系統(tǒng)安裝底座的下部加裝外減振器，之后將系統(tǒng)固聯(lián)到振動臺上；通過調(diào)整工裝，分別使得慣導(dǎo)系統(tǒng)的X、Y、Z軸沖天，進(jìn)而分別沿慣導(dǎo)系統(tǒng)的兩個水平軸方向、對角線方向進(jìn)行固定頻率線振動實(shí)驗(yàn)(圖 1所示)，這樣便實(shí)現(xiàn)了陀螺在各個方向誤差參數(shù)的充分激勵。

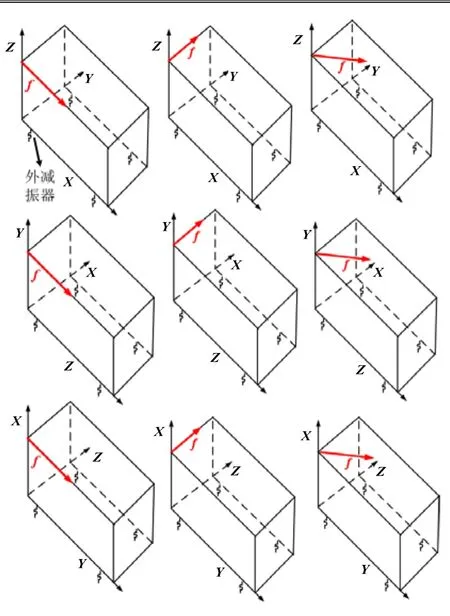
圖1 線振動實(shí)驗(yàn)示意圖Fig.1 Sketch of the linear vibration experiment

在振幅為2g，頻率為20 Hz正弦線振動條件下，按照誤差模型和標(biāo)定方法對某90型機(jī)抖激光陀螺捷聯(lián)慣導(dǎo)系統(tǒng)(圖2所示)待辨識參數(shù)進(jìn)行標(biāo)定，得到未知參數(shù)值。每組振動實(shí)驗(yàn)按照以下順序組織：慣導(dǎo)系統(tǒng)首先靜止10 min，然后振動10 min，最后再次靜止10 min。考慮到t0+T時刻的姿態(tài)參考矩陣的航向角誤差受等效東向陀螺漂移的影響較大，t0+T時刻的姿態(tài)誤差參考值只取水平姿態(tài)角誤差。

圖2 線振動實(shí)驗(yàn)Fig.2 Linear vibration experiment

在補(bǔ)償?shù)艏铀俣扔?jì)尺寸效應(yīng)和二次平方項(xiàng)誤差的基礎(chǔ)上，將辨識得到的參數(shù)用于振幅為 2g，頻率為40 Hz的正弦線振動實(shí)驗(yàn)誤差補(bǔ)償，驗(yàn)證誤差模型的補(bǔ)償效果。圖3給出了相應(yīng)時間段內(nèi)水平方向加速度、角速率乘積項(xiàng)的積分曲線圖4給出了補(bǔ)償前后速度誤差對比曲線。

圖3 積分曲線Fig.3 Integral curve

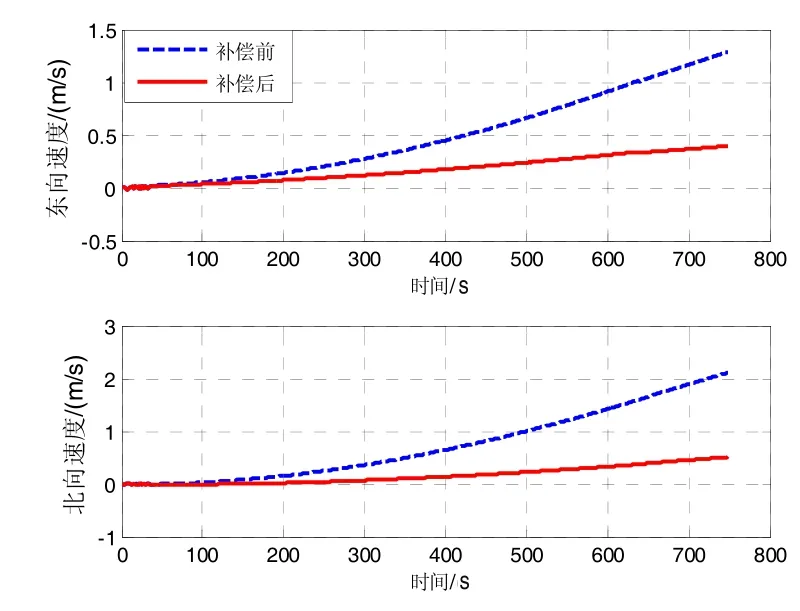
圖4 初步補(bǔ)償結(jié)果Fig.4 Preliminary compensation result

線振動時間約為10 min，考察補(bǔ)償前后的純慣導(dǎo)速度誤差。從圖3可以看出，線振動開始后水平方向加速度、角速率乘積項(xiàng)所對應(yīng)的積分值迅速增大，說明加速度和角速率之間耦合作用明顯，造成了相應(yīng)的姿態(tài)漂移。進(jìn)一步，從圖4可以看出，線振動條件下由于加速度和角速率之間的耦合作用，慣導(dǎo)系統(tǒng)速度誤差迅速增大，經(jīng)過補(bǔ)償后速度誤差減小 30%以上，精度改善明顯。

4 結(jié) 論

機(jī)抖激光陀螺敏感軸動態(tài)偏移誤差是造成振動環(huán)境下慣導(dǎo)系統(tǒng)精度下降的重要原因，本文建立了機(jī)抖激光陀螺敏感軸動態(tài)偏移的誤差模型，根據(jù)誤差模型設(shè)計(jì)了相應(yīng)的誤差參數(shù)標(biāo)定方法，并探討了標(biāo)定實(shí)驗(yàn)的組織實(shí)施形式。初步的實(shí)驗(yàn)結(jié)果表明，機(jī)抖激光陀螺敏感軸動態(tài)偏移誤差補(bǔ)償后，10 min線振動時間內(nèi)，系統(tǒng)純慣導(dǎo)速度誤差減小30%以上。

（References）：

[1] 劉昱, 王偉, 李城鎖. 激光陀螺捷聯(lián)慣導(dǎo)系統(tǒng) IMU結(jié)構(gòu)模態(tài)分析[J]. 中國慣性技術(shù)學(xué)報(bào), 2012, 20(3): 273-277. Liu Yu, Wang Wei, Li Cheng-suo. Modal analysis for IMU of ring laser gyro strap-down inertial navigation system[J]. Journal of Chinese Inertial Technology, 2012, 20(3): 273-277.

[2] 章博, 任娟. 捷聯(lián)慣組空間五點(diǎn)減振的振動耦合分析[J]. 宇航學(xué)報(bào), 2015, 36(9): 1030-1035. Zhang Bo, Ren Juan. Coupling vibration analysis of spatial-five-point arrangement isolators for strapdown inertial navigation system[J]. Journal of Astronautics, 2015, 36(9): 1030-1035.

[3] Li J L, Fang J C, Ge S S. Kinetics and design of a mechanically dithered ring laser gyroscope position and orientation system[J]. IEEE Transactions on Instrumentation and Measurement, 2013, 62(1): 210-220.

[4] Cheng J C, Fang J C, Wu W R, et al. Optimized design method of vibration isolation system in mechanically dithered RLG POS based on motion decoupling[J]. Measurement, 2014, 48: 314-324.

[5] Zlatkin Y M, Kainoguz A N, Voronchenko V G, et al. Laser SINS for Cyclone-4 launch vehicle[J]. Gyroscope and Navigation, 2013, 4(3): 156-163.

[6] Paul G S. Blazing gyros: the evolution of strapdown inertial navigation technology for aircraft[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(3): 637-655.

[7] Yu X D, Wei G, Long X W, et al. Finite element analysis and optimization of dither mechanism in dithered ring laser gyroscope[J]. International Journal of Precision Engineering and Manufacturing, 2013, 14(3): 415-421.

[8] Yu X D, Long X W. Parametric design of mechanical dither with bimorph piezoelectric actuator for ring laser gyroscope[J]. International Journal of Applied Electromagnetics and Mechanics, 2015, 47(2): 305-312.

[9] 趙小寧, 韓宗虎, 郭昕, 等. 橢圓錐動效應(yīng)對機(jī)械抖動激光陀螺振動特性的影響[J]. 中國慣性技術(shù)學(xué)報(bào), 2015, 23(2): 258-261. Zhao Xiao-ning, Han Zong-hu, Guo Xin, et al. Influence of elliptical coning motion effect on mechanically dithered RLG vibration performance[J]. Journal of Chinese Inertial Technology, 2015, 23(2): 258-261.

[10] Kim K, Park C G. Drift error analysis caused by RLG dither axis bending[J]. Sensors and Actuators, 2007, 133(2): 425-430.

Estimation and compensation for dynamic bending error parameters of mechanical dithered RLG sensitive axis

WANG Lin, WU Wen-qi, PAN Xian-fei, LI Geng
(1. College of Mechatronics Engineering and Automation, National University of Defense Technology, Changsha 410073, China; 2. College of Optoelectronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)

The dynamic bending error model of mechanical dithered RLG sensitive axis is derived to improve the navigation accuracy of SINS in vibration environment. In view of engineering application, a simplified dynamic bending error model of mechanical dithered RLG sensitive axis is established. Based on the simplified error model, the equivalent gyro drift’s coupling relationships with the specific force and the angular rate are derived, in which the equivalent gyro drift is caused by the dynamic bending errors of gyro sensitive axis. The dynamic bending errors are attributed to nine unknown parameters. To identify these parameters, a calibrate method is designed, and the principle for designing the calibration experiment is presented. Vibration experiments based on attitude error observations are conducted to estimate the unknown parameters, which show that the velocity error is decreased by 30% after compensating the dynamic bending errors within 10 min of linear vibration.

mechanical dithered RLG; sensitive axis dynamic bending; error model; parameter calibration

U666.1

：A

2016-08-06；

：2016-11-29

國家重大基礎(chǔ)研究計(jì)劃資助項(xiàng)目（6132180103-2）；專利申請?zhí)枺?01610543153.X）

王林（1987—），男，博士研究生，從事慣性導(dǎo)航系統(tǒng)研究。E-mail: wanglinshanda@163.com

聯(lián) 系 人：吳文啟（1967—），男，教授，博士生導(dǎo)師。E-mail: wenqiwu_lit@hotmail.com

1005-6734(2016)06-0828-04

10.13695/j.cnki.12-1222/o3.2016.06.023