基于BDS的導彈脫靶量數據處理方法

馬海潮

（92941部隊96分隊，葫蘆島 125001）

基于BDS的導彈脫靶量數據處理方法

馬海潮

（92941部隊96分隊，葫蘆島 125001）

研究利用導彈過靶前的測量數據解算脫靶量參數。針對導彈過靶時刻BDS（北斗系統）不能定位和測量數據丟失等問題，采用最優濾波平滑處理技術，建立過靶瞬間彈道外推數學模型，對導彈飛行軌跡外推，獲得過靶時的完整彈道參數。為解決靶船上合作目標部位不一致問題，利用導彈射向、彈道偏角、靶船航向信息和靶船上BDS天線相位中心相對于角反射體中心的位置，對合作目標部位進行修正，解算相對于角反射體中心的脫靶量參數。通過建立過靶痕跡方向判別坐標系，利用脫靶量參數，判別導彈過靶痕跡方向性。測試數據處理結果表明該方法精度高，脫靶量精度達到0.5 m。

導彈；外彈道測量；脫靶量；事后數據處理；最優濾波；北斗系統

在導彈武器系統試驗與鑒定中，脫靶量參數為檢驗武器性能中一項關鍵指標，直接用于判定導彈命中與否，關系到武器系統命中概率或質量。伴隨著先進精確制導技術[1-3]的發展，對脫靶量測量提出更高需求。脫靶量測量可采用聲學[4]、光學(可見光和紅外)[5]和無線電[6-7]等技術實現。光學脫靶量解算至少需兩臺經緯儀均有彈靶協同畫幅或圖像，且其精度受交會角大小影響[8]。受天氣影響，在能見度低、逆光情況下，經緯儀不能跟蹤測量目標。由于導彈武器裝備性能不斷提升，尤其射程的增大和末制導精度的提高，對脫靶量測量提出更新、更高要求。試驗區域地理條件難以滿足CCD、紅外光學經緯儀布站測量要求。因此，經緯儀難以完成大射程導彈遭遇段或中靶段圖像測量。無線電脫靶量測量原理主要是基于多普勒技術[9-14]。靶載無線電(連續波或脈沖式)脫靶量測量設備體積和質量都較大，安裝和標校復雜，且造價高，每套約百萬元以上[15]，因其易被擊中或振壞，試驗成本高，性價比低，經濟上難以承受。

隨著衛星導航定位技術的飛速發展，它具有了更加優異的性能，如定位精度高，測量范圍不受限，測量成功率高，全天候測量和全時空可用等。北斗導航系統 BDS測量已在航空航天測控領域得到了廣泛的應用，尤其是二代 BDS已成為武器系統試驗中目標跟蹤測量不可卻少的主要手段，它不僅用于導彈飛行試驗外彈道測量，而且還可實現彈靶遭遇段脫靶量測量。

1 導彈和靶船BDS測量差分定位

導彈和靶船 BDS測量差分定位由彈載、靶載BDS接收機或活動站、地面BDS基準站硬件及動態差分定位處理軟件等組成。彈載 BDS設備安裝于導彈合適位置，BDS天線接收導航衛星信號，接收機完成導彈單站自定位處理，并記錄原始導航信息，同時單站定位結果數據和原始導航信息經彈上遙測信道鏈路打包下傳至地面遙測接收設備；靶載 BDS設備安裝于靶船合適位置，接收并記錄導航衛星信息。地面基準站實時同步記錄 BDS導航衛星信息。彈載、靶載 BDS測量信息分別與基準站信息進行偽距或載波相位差分處理，獲得WGS-84坐標系下導彈飛行軌跡和靶船定位參數。導彈和靶船等目標的差分定位結果需轉換至發射坐標系下的目標數據。

下面分別給出地心大地坐標轉換與地心直角坐標、發射坐標系與地心直角坐標系等之間的轉換關系。

1.1 目標地心大地坐標與地心直角坐標的轉換

設i點的大地坐標經度、緯度、大地高為(Bi,Li,Hi)，則其地心直角坐標為

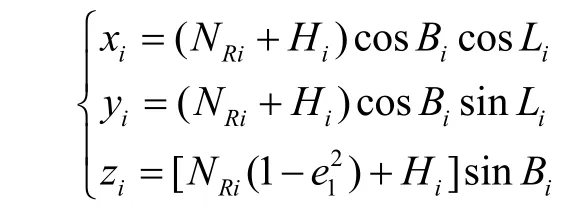
式中：NRi為i點的卯酉圈曲率半徑，e1為第一偏心率，

式中：a和b分別為WGS-84參考橢球體的長半軸和短半軸，即

1.2 目標發射坐標系與地心直角坐標系的轉換

設導彈在發射坐標系與地心直角坐標系下位置參數分別為Xf=(xf,yf,zf)T，Xd=(xd,yd,zd)T。發射坐標系原點的地心經度、緯度、射擊方位角或射向角分別為Lof、Bof、αof，在地心直角坐標系的坐標為Xof=(xof,yof,zof)T，Rx(φ)、Ry(φ)、Rz(θ)分別為繞x軸、y軸、z軸正旋轉φ、φ、θ (rad)角的旋轉矩陣，即

則地心直角坐標系到發射坐標系的轉換關系為

發射坐標系到地心直角坐標系的轉換關系為

2 過靶瞬間彈道外推數學模型

導彈于過靶時刻存在 BDS不能定位和測量數據丟失的問題。過靶前瞬間，彈上BDS接收機受靶船上桅桿、靶載設備或海雜波干擾影響，接收導航衛星數據質量很差，通常不能定位；受視距影響，岸基地面遙測設備不能接收彈上下傳的信息，導致過靶時的數據丟失。于是，造成過靶時彈道數據不完整性。若不補上丟失的數據，將無法解算脫靶量。

通常，利用中心平滑濾波方法對測量數據序列進行處理，解算彈道參數。然而，此方法將使得彈道參數結果初始處和結尾處損失或缺少若干幀數據，如單邊平滑點數1、2、3或4等，相應損失幀數1、2、3或4等，平滑點數越多，損失數據幀數越多。為了充分利用或不損失過靶前的原始測量數據，通過濾波外推或預測，解算出過靶時的導彈位置參數，以提高脫靶量質量和可信度。

過靶前測量數據即為濾波器的輸入x(t)可分解為

式中：P(t)為目標彈道飛行真實數據，ε(t)為平穩零均值的白噪聲。

設P(t)為一個p階多項式，可表示為

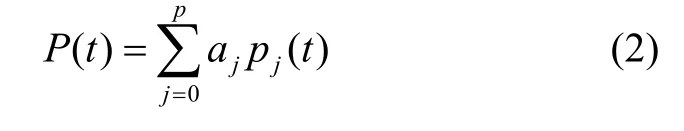
由最小二乘估計準則，可求得系數aj的估計值

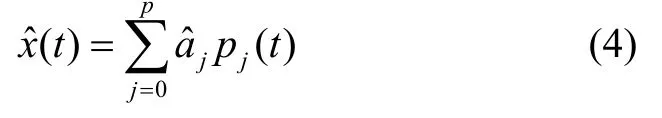
在t=（N+α）h時刻，L階微商的正交多項式最優線性濾波預測估值為

式中：正交多項式濾波權系數為

導彈過靶前或彈靶遭遇前至過靶間的飛行時間很短，其運動規律可視為勻速直線運動。為此，濾波器模型選用一階多項式擬合導彈測量真實狀態的函數。通過對測量數據進行一階多項式的濾波預測處理，可獲得t=(N+α)h時目標位置參數的濾波預測估計值。

當p=1，L=0，目標位置濾波預測的權序列及其方差比。由式(6)，可得：

3 合作目標部位修正

合作目標為靶船上的 BDS天線和角反射體，合作目標部位分別指靶船上的 BDS天線相位中心和角反射體中心。靶船上角反射體中心作為模擬目標中心，是導彈測試攻擊點。角反射體支架坐落于靶船甲板中心，BDS天線架設于靶船圍欄。需將靶船BDS天線定位結果轉換至相對于角反射體中心的靶船位置參數。

通過測量，可獲得 BDS天線中心相對于角反射體中心的位置(ΔL、ΔH、ΔW），其中，ΔL為BDS天線于靶船縱向相對角反射體中心的距離，ΔH為角反射體中心至靶船甲板與 BDS天線至靶船甲板的高度差，ΔW為BDS天線于靶船橫向相對角反射體中心的距離，如圖1所示。

通過坐標平移和旋轉，對靶船軌跡進行部位修正，得到相對于角反射體中心的靶船軌跡參數：

圖1 合作目標相對空間位置Fig.1 Relative position between cooperative objects

式中：(xs,ys,zs)為發射坐標系下靶船位置坐標；(xr,yr,zr)為于角反射體中心的靶船位置坐標；θ為發射坐標系下導彈航向角Kc與靶船航向角αs之差，即

4 脫靶量參數和過靶痕跡方向性

通過坐標轉換，將導彈于WGS-84坐標系下定位結果轉換至發射坐標系下導彈軌跡參數(xm,ym,zm)。利用目標位置濾波預測權序列式(7)和過靶瞬間彈道外推數學公式(5)，外推過靶前丟失的數幀導彈位置參數，獲得遭遇段完整的彈道參數，求取相對于角反射體中心的脫靶量參數。

令Δx(ti)=xm(ti)-xr(ti)，當導彈與靶船的X軸方向坐標相等時，所對應的時間te為導彈過靶時刻。也就是Δx(te)=0，即xm(te)=xr(te)時，可獲得導彈過靶時刻te及其縱向、側向偏差即脫靶量參數：

導彈打靶后，靶船拖回碼頭，要實地勘察和定性評估中靶或靶船毀傷情況。通常，命中靶標時，靶船上遺留有導彈過靶痕跡。吃水線以上的靶船船體、船甲板、圍欄、靶網、柱子、角反射體支架和角反射體等可能受損。中靶情況復雜，時常難以正確判別導彈從靶船哪個部位（左舷或右舷）穿入、穿出即過靶痕跡方向性。

利用脫靶量參數，通過建立過靶痕跡方向判別坐標系，解決過靶痕跡方向性判別問題。以 BDS天線相位中心為原點O，過原點O任意取平行于過靶痕跡一個方向為X軸指向，Y軸指向向上；Z軸與X軸、Y軸構成右手坐標系。過靶痕跡于Z軸不是正就是負方向，因此，判別過靶痕跡方向性分為兩種情況：

1）過靶痕跡于Z軸正方向

若Δz(te)＞0，過靶痕跡方向為X軸指向反方向；否則，過靶痕跡方向為X軸指向；

2）過靶痕跡于Z軸負方向

若Δz(te)＜0，過靶痕跡方向為X軸指向反方向；否則，過靶痕跡方向為X軸指向。

總之，當過靶痕跡于方向判別坐標系Z軸方向與脫靶量側向偏差為相同符號簡稱“同號”（正或負）時，過靶痕跡方向為X軸指向反方向；否則，過靶痕跡方向為X軸指向。

5 測試數據結果

利用過靶前導彈的9幀（N=9）BDS定位數據，先分別求得待外推 5個采樣點（α=1,2,3,4,5）的濾波預測權系數 W0,W1,…,W8，其次對導彈飛行軌跡外推，獲得導彈過靶時5個采樣點彈道參數（x, y, z），如圖2所示。BDS天線中心相對于角反射體中心的空間位置是ΔL為12.3 m，ΔH為7.5 m，ΔW為9.1 m，發射坐標系下導彈航向角Kc與靶船航向角sα之差θ為 32.2°。通過合作目標部位修正，得到發射坐標系下于角反射體中心的靶船位置坐標。當導彈與靶船于發射坐標系X軸方向坐標相等時，解得導彈脫靶量參數即縱向偏差Δy為3.2 m，側向偏差Δz為-9.6 m，其實際測量值分別為2.7 m、-9.3 m，兩者比對結果分別為-0.5 m、0.3 m，說明數據處理方法精度高。

在檢靶現場，通過建立過靶痕跡方向判別坐標系，依側向偏差數據判定導彈從靶船右舷穿入左舷穿出，這與實際靶船損傷痕跡相符。

圖2 導彈過靶瞬間彈道數據Fig.2 Trajectory data of missile in hitting a target

6 結 論

本文通過建立導彈過靶瞬間彈道外推數學模型，利用過靶前導彈的BDS定位數據，對導彈飛行軌跡外推，獲得過靶時的彈道參數；給出了合作目標部位修正公式，將靶船上BDS天線相位中心定位結果轉換至于角反射體中心的靶船位置參數；計算出了導彈攻擊靶船時相對于角反射體中心的縱向、側向偏差即脫靶量參數；通過建立過靶痕跡方向判別坐標系，解決了判別導彈過靶痕跡方向性問題。

（Reference）：

[1] Wang X H. Wang J Z. Partial integrated missile guidance and control with finite time convergence[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(5): 1399-1409.

[2] Sun S, Zhou D, Hou W T. A guidance law with finite time convergence accounting for autopilot lag[J]. Aerospace Science and Technology, 2013, 25(1): 132-137.

[3] Qu P P, Zhou D. Observer based guidance law accountting for second order dynamics of missile autopilots[J]. Journal of Harbin Institute of Technology, 2013, 20(1): 17-22.

[4] 石巖, 胡春曉. 基于聲學測量的艦炮對空脫靶量算法研究[J]. 艦船電子工程, 2014, 34(12): 179-182. Shi Yan, Hu Chun-xiao. Algorithm of antiaircraft missdistance for naval gun based on acoustic measurement[J]. Ship Electronic Engineering, 2014, 34(12): 179-182.

[5] 藺建英, 馬海潮. 基于單站序列圖像的導彈脫靶量測量方法[J]. 航天控制, 2013, 31(5): 41-45. Lin Jian-ying, Ma Hai-chao. Method of missile-target miss distance measurement based on single station sequence images[J]. Aerospace Control, 2013, 31(5): 41-45.

[6] Fischer A, Vuichard A, Berger H. Method and installation for estimating and displaying a shooting miss. European Patent: No.0862041B1[P]. 2001-04-04.

[7] Kerry Nicholas J, Utsi Per A V, Miles Upton E G, et al. Apparatus for and method of determining positional information for an object. US: No.6218983B1[P]. 2001.

[8] 周慧. 同幀畫幅測量導彈脫靶量精度分析[J]. 電子測量技術, 2015, 38(1): 83-86. Zhou Hui. Analyses of missile miss distance accuracy using the same frames measurement[J]. Electronic Measurement Technology, 2015, 38(1): 83-86.

[9] 馮定偉, 吳嗣亮, 魏國華. 基于多普勒頻差的矢量脫靶量參數估計方法[J]. 系統工程與電子技術, 2012, 34(8): 1530-1535. Feng Ding-wei, Wu Si-liang, Wei Guo-hua. Novel way of vector miss distance parameters estimation based on frequency difference of arrival[J]. Systems Engineering and Electronics, 2012, 34(8): 1530-1535.

[10] 韓路杰, 崔少輝. 利用導引頭信息測量脫靶量的方法[J]. 系統工程與電子技術, 2014, 36(4): 734-739. Han Lu-jie, Cui Shao-hui. Method of miss distance measurement using data of seeker[J]. Systems Engineering and Electronics, 2014, 36(4): 734-739.

[11] Liu Y P, Yong Q, Zhang P Q. Research on low-cost near-space and stealth target detection system[C]∥Proc. of the Intelligent Science and Intelligent Data Engineering Second Sino-Foreign-Interchange Workshop. 2012: 622-636.

[12] Foreman D C, Toumes C H. Trajectory shaping andprecision guidance of a spinning mortar without anglestate feedback[C]∥Proc. of the AIAA Guidance, Navigation and Control Conference. 2011: 1-11.

[13] Prasanna H M, Ghone D. Retro-proportional-navigation: a new guidance law for interception of high-speed target [J]. Journal of Guidance Control and Dynamics, 2012, 35(2): 377-386.

[14] Kalkan Y, Baykal B. Target localization and velocity estimation methods for frequency-only MIMO radars[C]∥Pro. of the IEEE Radar Conference. 2011: 458-463.

[15] 魏國華, 吳嗣亮, 王菊, 等. 脫靶量測量技術綜述[J].系統工程與電子技術, 2004, 26(6): 768-772. Wei Guo-hua, Wu Si-liang, Wang Ju, et a1. Overview of miss distance measurement technology[J]. Systems Engineering and Electronics, 2004, 26(6): 768-772.

Data processing method for missile’s miss-distance based on Beidou system

MA Hai-chao
(Unit 96 of PLA 92941, Huludao 125001, China)

This study focuses on utilizing the measurement data of a missile in pre-hitting a target to compute the miss-distance parameters. In view that the BDS (Beidou navigation system) usually can not locate the missile at the moment of hitting a target ship and the measurement data is always lost, a trajectory forecast model is set up by utilizing optimum filtering technique to extrapolate the missile-flying ending position parameter. By using such parameters as missile shot angle, trajectory angle, ship course, and the relative position between BDS antenna phase center and triangular trihedral reflectors’ center on a target ship, the BDS antenna phase center position is transferred into the triangular trihedral reflectors’ center position for computing the miss distance. A coordinate system for identifying the hitting-trace direction is set up, and the miss-distance parameters are used to recognize the direction property of a missile’s trace in hitting a target. Test results show that the proposed method has high accuracy, and the miss-distance error is no more than 0.5 m.

missile; trajectory measurement; miss distance; post-flight data processing; optimum filtering; Beidou system

TJ06

：A

2016-07-30；

：2016-09-28

馬海潮（1962—），高工，博士，主要研究方向為外測事后數據處理分析和精度評估。Email: mhcsea@163.com

1005-6734(2016)06-0845-04

10.13695/j.cnki.12-1222/o3.2016.06.026