“平均數”的教學要重視其統計意義
陳繁榮
?
“平均數”的教學要重視其統計意義
陳繁榮

“平均數”的教學,人教版教材原先安排在三年級下冊,現移至四年級下冊。教材上安排了兩個例題,例1是教學平均數的含義和求法,例2是讓學生理解比較兩組數據的總體情況時,用平均數比較合適。教學目標是:使學生理解平均數的含義,學會簡單的求平均數的方法,體會平均數在統計學中的作用,并能夠用自己的語言解釋其實際意義。
在統計中,算術平均數常用于表示統計對象的一般水平。它是描述數據集中程度的一個統計量,既可以用來反映一組數據的一般情況(用平均數表示一組數據的情況,有直觀、簡明的特點),也可以進行不同組數據的比較,可以看出組與組之間的差別。用平均數作為一組數據的代表,比較可靠和穩定,它與這組數據中的每一個數都有關系,對這些數據所包含的信息的反映最為充分,因而應用最為廣泛,特別是在進行統計推斷時有重要作用。求平均數的方法并不難,理解平均數的意義應是本課的重點。教材在習題中安排了不少讓學生理解平均數統計意義的題目。這些題目并不單純是計算平均數,更多的是運用平均數的統計含義解決問題,幫助學生進一步理解平均數的意義。
在平均數中有一種去尾平均數,它是將一組數據中的一個最大值和一個最小值去掉后再求其余數值的平均數。它保留了平均數的集中趨勢代表性強的優點,又具有中位數的可排除個別數據變動較大所帶來的影響的特點,因而當一組數據的個數較少、且可能個別數據變動較大時,常用去尾平均數描述一組數據的集中趨勢。平均數反映一組數據的總體情況比中位數、眾數更為可靠、穩定。平均數的缺點是需要整批數據中的每一個數據都加入計算,因此,在數據有個別缺失的情況下則無法準確計算。一組數據的每一個數據都要參加計算才能求出,特別是當一組數據的數量較大時,其計算的工作量也較大。平均數易受極端數據的影響,從而容易讓人對平均數產生懷疑。這也就是在許多競賽中對評委亮分后的成績分數要去掉一個最高分和一個最低分,再計算平均數的原因。針對這一缺點,教材在練習中以選做題(如下圖)的形式讓學生在解決問題中有所體會,以進一步豐富學生對平均數特點的認識。

下面是筆者聽到的一堂“平均數”教學片段,從中我們可以得到一些啟發。
【片段一】
師:(出示分別裝有5支、6支和7支筆的3個筆筒)誰能只移動1支筆,使每個筆筒里的筆一樣多呢?(指名一位學生上臺操作)說說你是怎么想的。
生:從最多的裝有7支筆的筆筒里拿出1支放到最少的裝有5支筆的筆筒里。
【片段二】
師:你們喜歡什么體育運動?
生:喜歡踢足球、打籃球……
師:下面是兩個隊進行投籃比賽(每人投10次)投中個數的示意圖。你認為哪隊的實力強呢?你是怎么知道的?
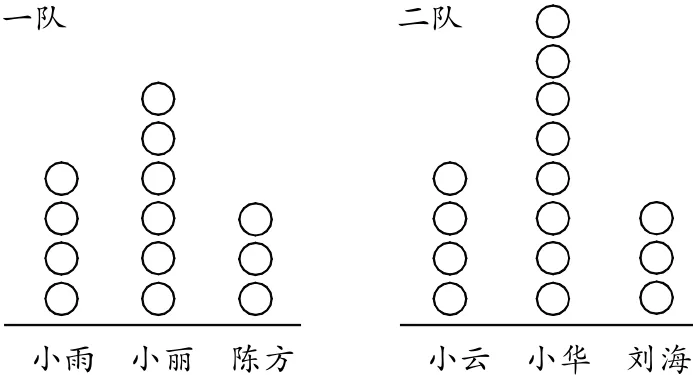
生1:二隊的實力強些。因為二隊共投中了15個球,一隊只投中了13個球。
生2:二隊有1個人投中的個數最多。
師:(出示下圖)你認為哪隊的實力強呢?你是怎么知道的?
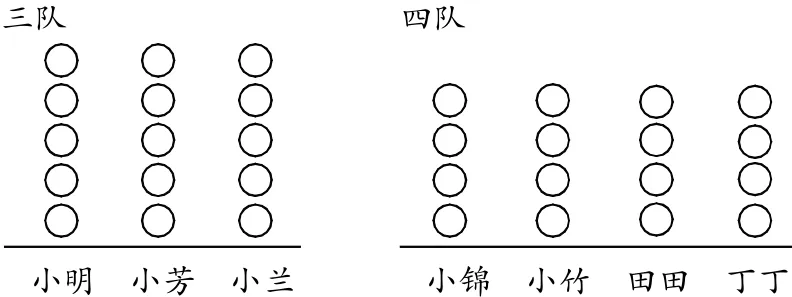
生3:四隊的實力強,因為四隊共投中了16個球,三隊只投中了15個球。
生4:不能用總數比較,因為四隊多1個人參加比賽。應該是三隊的實力強,他們每個人都投中了5個球,四隊每個人都只投中4個球。
師:(出示下圖)你認為哪隊的實力強呢?你是怎么知道的?

學生分組討論,師指名學生上臺操作(如下圖所示)。
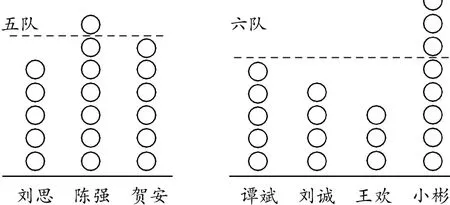
生5:五隊的實力強,平均每個人投中了6個球,六隊平均每個人只投中了5個球。
師:你們是怎么算出平均數的?
生6:列式計算。
教材上的例題是小紅、小蘭、小亮和小明四人一組共收集52個礦泉水瓶,要求平均每個人收集了多少個,內容是采用象形和條形統計圖來呈現的。這里的教學片段選擇的教學內容是學生投籃比賽,比較兩個隊的實力強弱,內容的呈現具有層次性,有利于學生的體驗與理解、思考與探索。學生通過活動,體會到了學習平均數的必要性和平均數的統計意義,即平均數能較好地反映一組數據的總體情況。遺憾的是活動后教師沒有讓學生反思。其實,教師可以提問:在人數不相等的情況下怎樣比較兩隊的實力?通過平均數的學習,你感覺到平均數有什么作用?有什么特點?——平均數比這組數據中最大的數要小,比最小的數要大。
(作者單位:攸縣酒埠江鎮中心小學)