基于單向流固耦合技術潛射導彈出筒載荷研究*

張 劍,楊 鳴

(1 中國空空導彈研究院,河南洛陽 471000;2 四川航天技術研究院,成都 610100)

基于單向流固耦合技術潛射導彈出筒載荷研究*

張 劍1,楊 鳴2

(1 中國空空導彈研究院,河南洛陽 471000;2 四川航天技術研究院,成都 610100)

為研究潛射導彈出筒過程中受載特性,基于單向流固耦合技術建立了導彈發射動力學數學模型,分析了兩種艇速條件下導彈出筒過程中所受到的截面彎矩載荷。通過和縮比試驗測試結果對比,表明仿真結果具有可信性。計算結果表明,導彈受載危險截面集中在彈身中部偏后的位置,且艇速對導彈受載和初始偏轉角有重要影響。文中建模方法和計算結果對潛射導彈結構總體設計具有指導意義。

潛射;載荷特性;單向流固耦合

0 引言

潛射導彈發射過程可以分為離筒段、水中段和出水段三部分。對采用彈射發射方式的潛射導彈來說,在離筒段主要承受流體動力、慣性力和彈-筒間接觸力的作用。離筒段載荷計算結果是導彈結構與強度設計以及發射方案制定必須考慮的因素,直接關系到導彈發射的安全性與可靠性。文獻[1]利用軸對稱模型,采用MPCCI實現FLUENT和ABAQUS數據交換,得到導彈出筒過程的結構響應。文獻[2]依據縮比試驗獲取的載荷數據,假設導彈迎水面和背水面壓力滿足正弦分布,利用ABAQUS自帶的VDLOD用戶子程序將壓力外載荷以插值形式添加到潛射導彈發射動力學模型當中,獲取了不同出筒條件下導彈所受載荷特性。

文中以流固耦合分析技術為基礎,采用直接單向耦合方法[3],以ABAQUS-MPCCI-FLUENT為仿真建模平臺,分析了艇速對導彈受載特性的影響。

1 導彈發射載荷縮比測試試驗

1.1 導彈截面彎矩載荷的獲取

在滿足結構動力和流體動力相似性[4-6]條件基礎上進行導彈出筒過程縮比試驗,試驗主要目的是獲取導彈特征截面在2.1 kn和4.3 kn兩種艇速條件下彎矩載荷變化規律及導彈質心沿初始射向運動規律,相似比λ=3.38。測試截面I在實際導彈結構中距彈頂4 500 mm,截面II距彈頂5 000 mm。測量截面處使用測力天平連接,分段處留下一定間隙,間隙大小以保證兩截面不發生碰撞為標準。

圖1 測試截面位置示意圖

1.2 縮比試驗結果分析

從位移歷程和速度歷程可以看出,在給定推力的情況下,除了初始運動尚不穩定的一小段以外,導彈的運動明顯呈現出類似勻加速運動的特點,位移歷程形狀類似一條開口向上的拋物線,而速度歷程曲線則類似由多段直線構成。由此可知,導彈出筒過程中所受到的多種作用力共同合成了一個近似恒定的合力作用,在模擬潛射導彈發射時,將導彈運動簡化為勻加速運動是有足夠依據的。另外,在4.3 kn艇速條件下,導彈出筒速度較2.1 kn為小,相應位移也小一些,這是因為在較高艇速條件下發射,導彈偏轉姿態角增大。一方面,導彈偏轉角度增大后豎直方向迎水面面積和2.1 kn時相比變大從而受到了更大的流場阻力;另一方面,橫向流速度的加大使得導彈與發射筒之間接觸作用力變大,從而導致出筒阻力的增加。上述兩點原因導致導彈離筒速度降低。

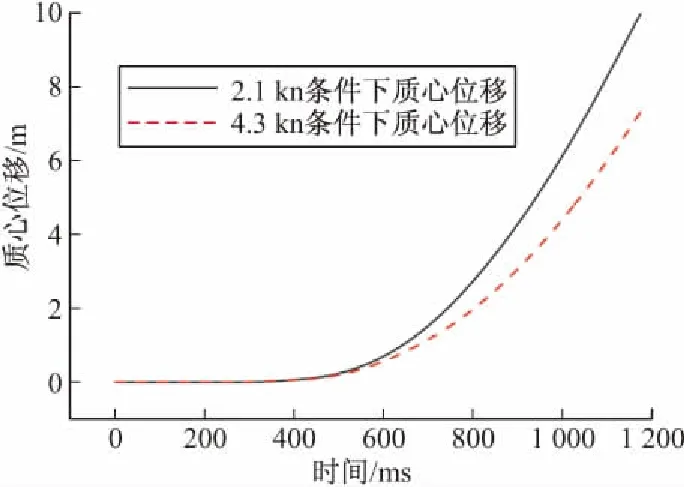
圖2 兩種艇速條件下導彈質心位移變化規律

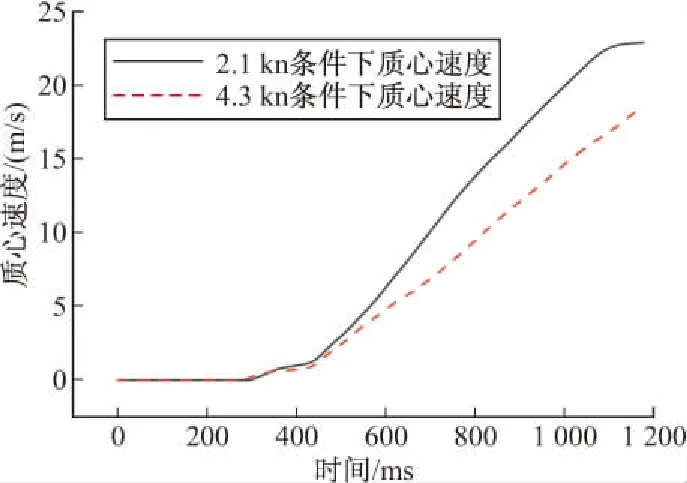
圖3 兩種艇速條件下導彈質心速度變化規律

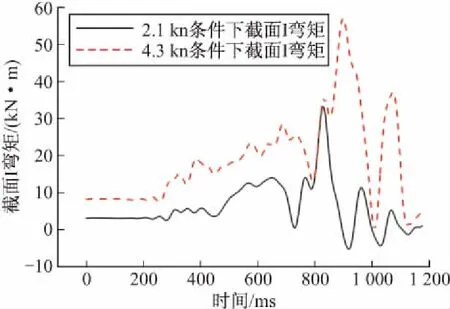
圖4 兩種艇速條件下截面I彎矩載荷變化規律

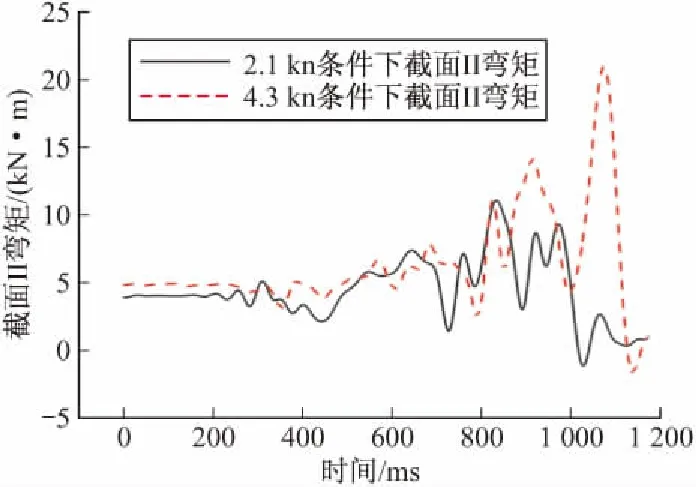
圖5 兩種艇速條件下截面II彎矩載荷變化規律

對比橫向彎矩的測試結果發現,高艇速條件下同一個截面位置處其彎矩載荷要大得多。因此艇速的增加直接引起了導彈受載的加劇,必須對導彈發射時潛艇的速度加以控制防止導彈受載過大。

2 數學模型的建立

2.1 導彈結構模型與材料

假設整個模型具有面對稱性,只取導彈和發射筒結構的一半建模,其中導彈彈身直徑534 mm,彈長7 300 mm,發射筒直徑538 mm,兩者間隙為2 mm。結構模型使用S4R殼單元,即線性、有限薄膜應變、減縮積分、四邊形殼單元[7]和集中質量點單元按照1∶1的比例關系來模擬導彈和發射筒結構,按照面對稱假設,集中質量點質量均為實際質量的一半。將導彈的外表面區域設置為耦合計算面。導彈和發射筒間的接觸算法類型設置為通用接觸。計算結果中將包含截面I和截面II處彎矩載荷。導彈和發射筒的幾何結構如圖6所示。

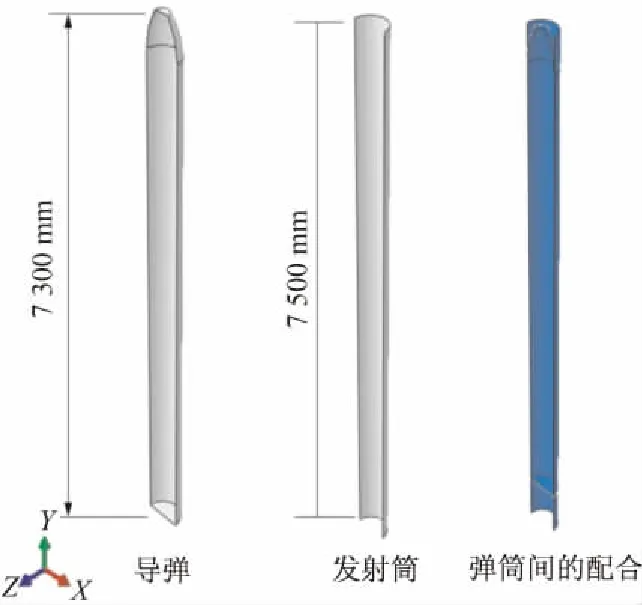
圖6 導彈和發射筒的幾何結構示意圖

發射筒上下兩個端面設置為固定邊界條件。導彈在發射過程中的運動軌跡控制采用“速度-時間”驅動,在結構模型中,指定導彈彈體底部端面圓心為一個點集合并建立一個參考點,然后建立這一參考點和彈底端面的MPC約束,依據試驗測得的兩種艇速條件下的“速度-時間”規律創建幅值曲線,再在這一參考點添加速度邊界條件,將邊界條件的變化規律指定為對應的幅值曲線便完成了結構模型中導彈彈體運動規律的設置。在流場模型當中,依據同樣的“速度-時間”變化規律,編制profile文件對導彈壁面運動加以控制。2.2 湍流模型與多相流模型流場計算主要使用標準k-ε模型[8],模型認為湍動粘度μt是湍動能k與湍動耗散率ε的函數。

(1)

k與湍動耗散率ε滿足:

Gk+Gb-ρε-YM+Sk

(2)

(3)

式中,Gk是由平均速度梯度帶來的湍動能k發生項,Gb是因為浮力貢獻而帶來的湍動能k發生項,YM由可壓縮湍流脈動擴張引起。

導彈離筒過程中,筒內原有均壓氣體會隨同導彈一起進入海水介質中。受海水阻滯作用,筒口氣體不能很快擴散,在筒口形成復雜的筒口流場。為了描述筒口流場的水-氣兩相流運動,使用VOF模型描述多相流動[9]:

模型的連續方程為:

(4)

式中:mpq代表第p相向第q相的質量輸運,反之亦然;Saq代表源項,默認情況下為0。

利用平均密度和平均粘度系數來求解單一的動量方程:

(5)

利用平均能量來求解單一的能量方程:

(6)

式中keff被稱為有效導熱系數。由動量和能量方程可以看出,由于使用了加權平均,當相間速度、溫度(能量)差別較大時,VOF模型計算結果誤差也將較大,故該模型比較適合流場變量梯度相對較小的彈射發射流場計算。

計算水深設定為30 m,且假設發射時筒內已經預先注入起到平衡外界海水靜壓作用的均壓氣體。

2.3 流場區域網格的劃分及動網格技術的應用

就單向耦合模型而言,在流場中只計入導彈沿其軸向的運動,只需用到域動鋪層法即可。圖7展示了單向耦合方案條件下動網格設計的思路:將流場區域分為靜區域與動區域兩部分,在彼此分界面處用Interface條件聯接,動區域邊界與發射筒壁面重合,整個計算域都劃分為結構化網格。圖8則展示了流場模型中的各類邊界條件設置,其余邊界均為壓力出口條件。

圖7 動網格方案

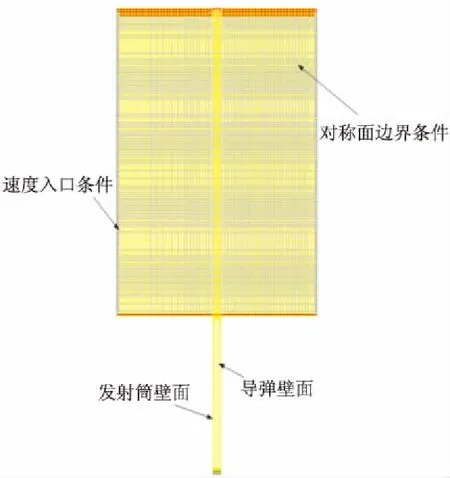
圖8 流場模型中的邊界條件

2.4 耦合計算過程中數據的交換

在單向耦合的計算條件下,流體壓力作用在導彈結構上,而結構的變形不會影響到流體。其思路可以表述為,在每一個時間步中,從流體方程Ff[Xf,0]=0中解出壓力Xf,流體模型中位移是零。再從結構方程FS[XS,Xf]=0中求出結構位移變量XS。單向耦合具體實施辦法可以分為兩種:一是記錄下導彈離筒過程中彈壁上若干測試點壓力隨時間變化規律,再編制相應的插值程序,將這些壓力數據添加到結構模型中完成結構載荷的計算,稱之為間接單向耦合算法;二是采用實時的辦法,在每一個計算時間步內傳遞數據,稱之為直接單向耦合算法。采用第一種辦法,流場和結構的計算是完全分開的,不需要第三方插值程序的介入,但需要編制獨立的壓力載荷插值程序,要保證精度就必須設置足夠多的壓力測試點,這是其不足之處。采用第二種辦法,借助第三方插值程序(MPCCI)實時地由流場模型向結構模型傳遞載荷數據,不需要編制獨立的載荷插值程序,且流場計算和結構計算可以同步進行,同步完成,另外,插值的時候,程序將自動使用彈壁上所有網格點的壓力數據,只要彈壁網格劃分的足夠細密,則計算精度是有保證的。使用第二種辦法有兩點需要注意:一是時間步的控制需要由流體模型決定;二是流場模型和結構模型中導彈位形相差不可太大以避免載荷數據和實際情況差別過于明顯而得不到正確的解,采用2.1節所述“速度-時間”驅動策略可以很好的滿足這一點。

3 數值計算結果分析

3.1 運動學計算結果分析

從姿態角的計算結果可以看出,首先,在導彈出筒過程的前半段,由于彈身入水部分較短,橫向來流的作用尚不充分,故姿態偏轉角接近于0。到了0.6 s以后,導彈姿態角開始急劇增加,到了離筒時刻前后導彈后端完全脫離發射筒的約束,姿態角出現“陡增”;其次,4.3 kn艇速條件下的離筒姿態角遠大于2.1 kn艇速條件下的結果,增長幅度達80%。從保持運載平臺的機動性和可操縱性角度看,希望發射導彈時艇速盡可能高,而對采用垂直發射方式的導彈而言,從減小彈體承受載荷和保證后續水彈道穩定的角度看,又希望艇速保持在較低水平,因此確定合理的發射艇速是制定發射方案時的一項重要內容。

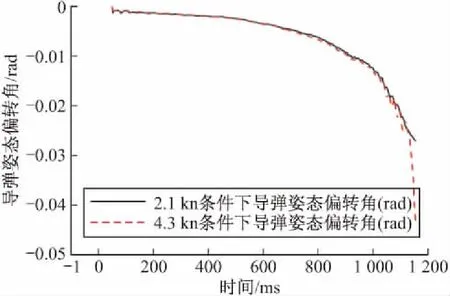
圖9 兩種艇速條件下的姿態角變化

3.2 動力學計算結果分析

圖10～圖11為導彈兩個測試截面在兩種艇速條件下計算得到的彎矩-時間歷程,通過和試驗測試結果對比,可以得到如下結論:

1)就載荷幅值而言,計算值和試驗測試值比較接近,說明建模方法具有可信度;

2)從彎矩載荷出現的位置來看,導彈受載危險截面為彈身中間偏后位置;

3)艇速的增加明顯增大了導彈截面所受彎矩載荷,這和試驗測試結果是相符的;

4)計算得到的載荷趨勢和測試值之間存在一定差異,造成這種差異原因在于沒有在流場模型中計入導彈姿態偏轉,導致作用于彈身表面流場壓力載荷和實際情況相比存在差異。

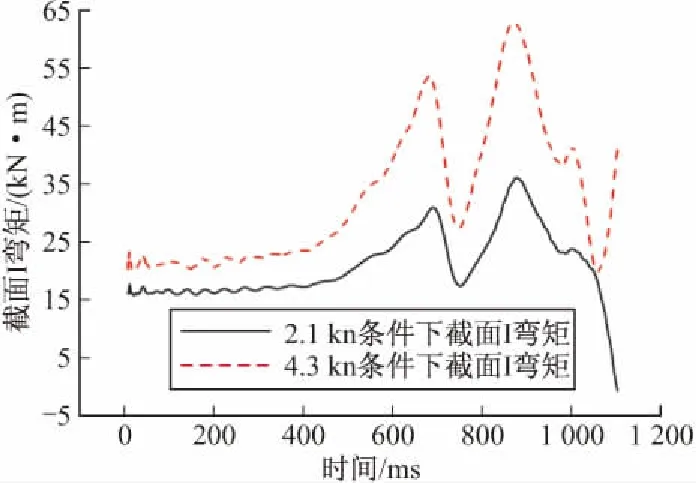
圖10 兩種艇速條件下截面I彎矩計算值

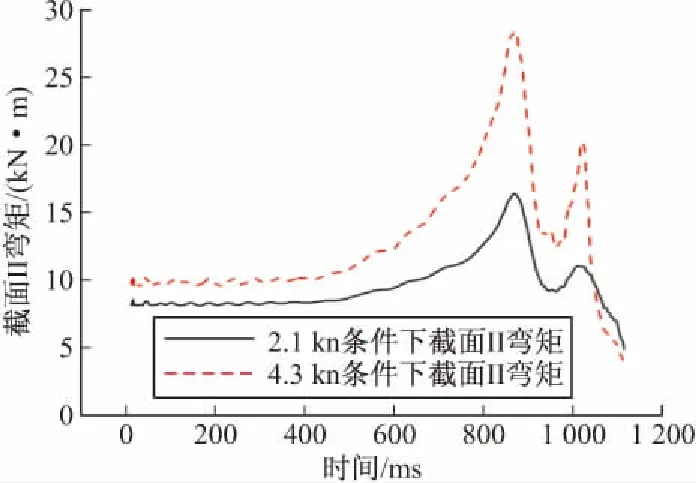
圖11 兩種艇速條件下截面II彎矩計算值

4 結論

文中采用單向流固耦合技術建立潛射導彈出筒載荷計算模型,通過和試驗測試結果對比,計算結果具有可信度。文中建模方法和計算結果對潛射導彈結構總體設計具有重要指導意義。在后續工作中還應當圍繞以下幾個方面進一步改進模型:

1)由于動網格技術使用方面的困難,未能在流場計算模型中計入導彈姿態運動,應當進一步建立更加完備的雙向流固耦合模型;

2)應當在模型中進一步計入發射過程中潛艇的下沉、搖晃等運動,因為發射平臺的運動會反過來影響導彈受載,要開展這部分工作尚需依賴硬件平臺性能的大幅提升。

[1] 馬慶鵬. 潛射航行體出筒過程載荷特性的數值模擬研究 [D]. 哈爾濱: 哈爾濱工業大學, 2011.

[2] 劉兵. 水下垂直發射的載荷研究 [D]. 北京: 北京理工大學, 2012.

[3] 岳戈. ADINA流體與流固耦合功能的高級應用 [M]. 北京: 人民交通大學出版社, 2010: 78-96.

[4] 苗瑞生, 居賢銘, 吳甲生. 導彈空氣動力學 [M]. 北京: 國防工業出版社, 2006: 117-124.

[5] 劉寶鏞. 全尺寸模型彈水下發射試驗的有關問題 [J]. 導彈與航天運載技術, 2000(4): 1-4.

[6] 黃壽康. 流體動力·彈道·載荷·環境 [M]. 北京: 中國宇航出版社, 1991: 21-38.

[7] 莊茁, 由小川, 廖劍暉, 等. 基于ABAQUS的有限元分析和應用 [M]. 北京: 清華大學出版社, 2009: 9-12.

[8] 閻超. 計算流體力學方法及其應用 [M]. 北京: 北京航空航天大學出版社, 2006: 228-239.

[9] 溫正. FLUNT流體計算應用教程 [M]. 2版. 北京: 清華大學出版社, 2013: 108-116.

Launching Load Study of Submarine Missile Based on One-way Fluid-solid Coupling

ZHANG Jian1,YANG Ming2

(1 China Airborne Missile Academy, Henan Luoyang 471000, China;2 Sichuan Academy of Aerospace Technology, Chengdu 610100, China)

For the study of load characteristics of submarine launched missile, the mathematical model of missile launching dynamics was established based on one-way fluid-solid coupling technique, and the cross section bending load under the condition of two kinds of ship speed was analyzed. The comparison of the simulation results and the test results showed that the simulation results were reliable. The calculation results showed that the missile loading dangerous cross section concentrated in the middle of the body after the position, and the boat speed had important effect on missile loading and initial deflection angle. In this paper, the modeling method and the results of the calculation had guiding significance for the overall structure design of the submarine launched missle.

submarine launched; load characteristics; one-way fluid-solid coupling; dynamic mesh

2015-12-07

張劍(1986-),男,河南南陽人,工程師,碩士,研究方向:導彈發射技術。

V41

A