基于概率模型的彈道導(dǎo)彈防御系統(tǒng)攔截方案優(yōu)化與評估
高昂,胡延蘇(.西北工業(yè)大學(xué)電子信息學(xué)院,陜西西安7007; .長安大學(xué)電子與控制工程學(xué)院,陜西西安70064)
?
基于概率模型的彈道導(dǎo)彈防御系統(tǒng)攔截方案優(yōu)化與評估
高昂1,胡延蘇2
(1.西北工業(yè)大學(xué)電子信息學(xué)院,陜西西安710072; 2.長安大學(xué)電子與控制工程學(xué)院,陜西西安710064)
摘要:針對彈道導(dǎo)彈防御系統(tǒng),研究概率意義下如何根據(jù)高層戰(zhàn)略防御指標(biāo)設(shè)計和部署攔截方案。在Bernoulli實(shí)驗(yàn)?zāi)P突A(chǔ)上,將攔截彈數(shù)量和防御指標(biāo)進(jìn)行關(guān)聯(lián),并進(jìn)一步分析系統(tǒng)廣義跟蹤能力以及攔截彈單發(fā)毀傷概率對所需攔截彈數(shù)量的影響。在此基礎(chǔ)上采用齊射攔截方式和連續(xù)發(fā)射方式,討論防御指標(biāo)、目標(biāo)數(shù)量、目標(biāo)威脅比率等因素對攔截彈消耗情況的影響。針對分層防御將各層攔截方案的設(shè)計建模為最優(yōu)化問題,在保證防御指標(biāo)的情況下,通過優(yōu)化各層目標(biāo)發(fā)射攔截彈的數(shù)量,使得平均每目標(biāo)消耗的攔截彈數(shù)量最少,從而達(dá)到整體作戰(zhàn)效能最優(yōu)。
關(guān)鍵詞:系統(tǒng)評估與可行性分析;彈道導(dǎo)彈防御系統(tǒng); Bernoulli模型;攔截
0 引言
彈道導(dǎo)彈具有重大的戰(zhàn)略、戰(zhàn)術(shù)威懾作用,已經(jīng)成為影響各國外交政治格局、左右戰(zhàn)場態(tài)勢、甚至決定戰(zhàn)爭勝負(fù)的重要因素。彈道導(dǎo)彈技術(shù)是國家國防實(shí)力的標(biāo)志和國際地位的重要象征。目前,世界上至少有8個發(fā)達(dá)國家和15個發(fā)展中國家能夠制造彈道導(dǎo)彈。隨著軍事技術(shù)的發(fā)展,導(dǎo)彈的投放系統(tǒng)越發(fā)的靈活,射程和精度也在不斷地提高,隱身、變軌、干擾、多彈頭技術(shù)的應(yīng)用,使得導(dǎo)彈的突防能力不斷增加;部分國家仍然在持續(xù)發(fā)展彈道導(dǎo)彈的大規(guī)模殺性武器運(yùn)載能力。并且,隨著世界多極化、科技全球化深入發(fā)展,國家地區(qū)之間軍事合作日趨廣泛而頻繁,彈道導(dǎo)彈技術(shù)的擴(kuò)散給防御系統(tǒng)帶來極大的困難和挑戰(zhàn)[1-2]。
目前,針對彈道導(dǎo)彈攔截方案優(yōu)化研究大多是采用最優(yōu)化方法對攔截彈進(jìn)行軌道優(yōu)化[3]或者采用效能評估理論對不同作戰(zhàn)條件下攔截效果進(jìn)行分析,進(jìn)而選擇最優(yōu)攔截方案[4-6]。然而,針對彈道導(dǎo)彈防御逐漸顯現(xiàn)的層次化特點(diǎn)[7],如何在保證高層防御指標(biāo)的情況下,優(yōu)化各層攔截方案特別是攔截彈分配問題,目前國內(nèi)外尚無統(tǒng)一理論;另一方面,對于“如何根據(jù)高層戰(zhàn)略防御指標(biāo)的要求,設(shè)計反導(dǎo)系統(tǒng)的戰(zhàn)技指標(biāo)并進(jìn)而形成有效部署”這一問題尚無定論[1,8]。換言之,目前要解決的是“怎樣規(guī)劃和部署攔截方案,以實(shí)現(xiàn)特定的防御任務(wù)”。本文針對這兩個問題,在Bernoulli實(shí)驗(yàn)?zāi)P突A(chǔ)上,通過優(yōu)化各層每目標(biāo)發(fā)射攔截彈的數(shù)量,對高層防御指標(biāo)進(jìn)行分解,使得平均每目標(biāo)消耗的攔截彈數(shù)量最少,從而達(dá)到整體作戰(zhàn)效能最優(yōu)。通常,衡量反導(dǎo)系統(tǒng)的能力可以有多種描述,例如:針對某一規(guī)模的來襲目標(biāo)數(shù)量,做到完全攔截;或者以某一指標(biāo)概率殺傷目標(biāo);或是攔截系統(tǒng)能夠以指定概率保護(hù)敏感區(qū)域不被擊中。以國家導(dǎo)彈防御(NMD)系統(tǒng)為例,在設(shè)計之初的設(shè)計指標(biāo)為:95%的置信概率下能夠攔截95%的來襲目標(biāo),即95%概率不超過1/20的目標(biāo)逃逸。本文同樣采用這種方法描述攔截指標(biāo)。
理論上,助推段攔截的效果要好于中段和再入段攔截,但事實(shí)上,助推段攔截對探測跟蹤以及攔截站的部署都提出了更高的要求。一方面,助推段時間一般較短,平均180~600 s,要求助推段防御系統(tǒng)具備快速反應(yīng)時間、高可信度決策能力,并且助推段攔截針對的目標(biāo)是導(dǎo)彈彈體而不是彈頭,繼續(xù)飛行的彈頭可能落在發(fā)射點(diǎn)和預(yù)定目標(biāo)之間,仍然存在一定的威脅;另一方面,助推段攔截要求攔截站應(yīng)該部署在發(fā)射點(diǎn)400~1000 km以內(nèi),對于縱深較大的國家,不具備在其周圍部署海基或陸基攔截站的條件,另一種可行的方法是通過部署空基和天基攔截器進(jìn)行攔截,但目前天基和空基激光器尚處于實(shí)驗(yàn)室研究階段。本文的討論重點(diǎn)為飛行段和再入段導(dǎo)彈彈體釋放彈頭以后的攔截過程。
1 Bernoulli實(shí)驗(yàn)?zāi)P?/h2>
通常彈道導(dǎo)彈會攜帶多枚真實(shí)的彈頭和誘餌彈以提高突防能力和被攔截的難度。
假設(shè)1 飛行段或再入段導(dǎo)彈彈體釋放彈頭和誘餌的時候,彈體所攜帶的所有威脅目標(biāo)一次性釋放完畢,不存在多次釋放的情況。
對于誘餌的識別方法主要是與真實(shí)彈頭的雷達(dá)特征、紅外特征、運(yùn)動特征等進(jìn)行比對,但由于軍事和技術(shù)保密等條件的限制,無論是彈頭還是誘餌的信號特征都很難在交戰(zhàn)前預(yù)知,只有在彈頭釋放以后進(jìn)行實(shí)時比對和判斷,特別是由于再入段時間太短(60~90 s),識別難度很大。誘餌彈和真實(shí)彈頭的識別率是反導(dǎo)系統(tǒng)重要的技術(shù)指標(biāo)。用pww表示正確識別彈頭的概率,pwd表示彈頭被誤判為誘餌的概率;pdd表示誘餌被正確識別的概率,pdw表示誘餌被誤判為彈頭的概率,顯然有pww=1-pwd,pdd=1-pdw.假設(shè)在一次攻擊中實(shí)際存在W個彈頭和D個誘餌,則反導(dǎo)系統(tǒng)中識別出的彈頭數(shù)量可以表示為
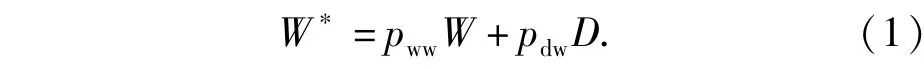
目標(biāo)成功突防反導(dǎo)系統(tǒng)不外乎兩種情況:1)彈頭被正確的識別,但攔截系統(tǒng)沒有成功攔截;2)彈頭被誤判為誘餌。所以,彈頭突防成功概率可表示為
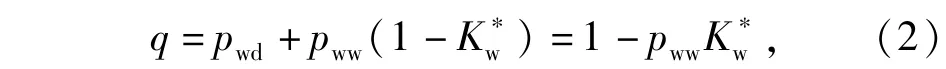
式中:K*w為彈頭正確識別條件下成功攔截的條件概率。則有
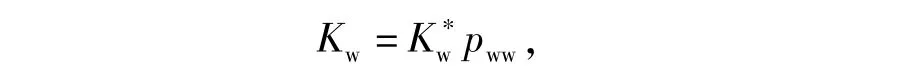
式中:Kw為彈頭正確識別和成功攔截的聯(lián)合概率,即反導(dǎo)預(yù)警的目標(biāo)毀傷概率。
整個彈道導(dǎo)彈攔截過程服從Bernoulli實(shí)驗(yàn)?zāi)P蚚1,8-11],p(χ)表示為W個彈頭的攔截試驗(yàn)中,有χ個彈頭未被成功攔截的概率,χ服從二項(xiàng)分布,則p(χ)可表示為
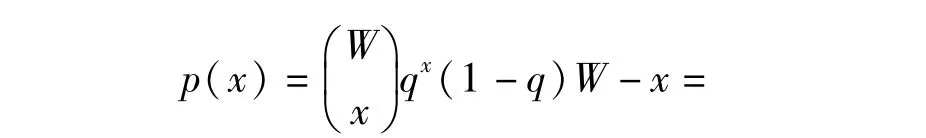
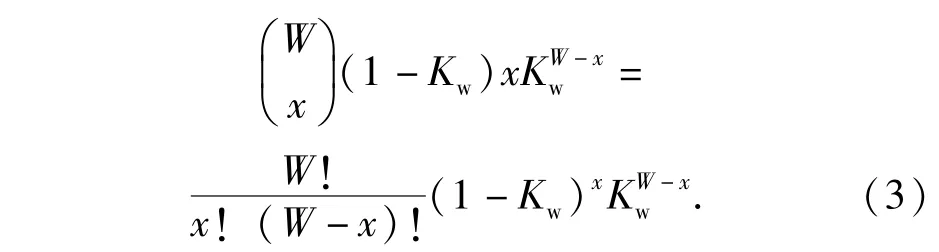
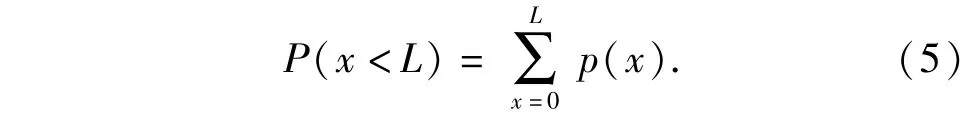
2 目標(biāo)毀傷概率
假設(shè)對所有威脅目標(biāo)的攔截概率獨(dú)立同分布, K = Kw.當(dāng)χ=0時,即所有的目標(biāo)都被成功攔截,由(3)式得
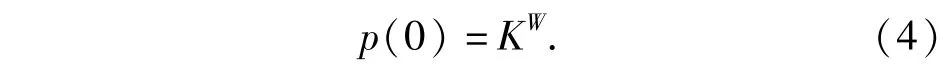
(4)式表示的攔截指標(biāo)可以表示為p0(W),即系統(tǒng)能夠以p0(W)的概率保證W個來襲目標(biāo)不會逃逸。如果攔截指標(biāo)是以容許最大逃逸目標(biāo)數(shù)量L的概率p(χ<L)表示,則
假設(shè)2 目標(biāo)毀傷概率是指目標(biāo)被擊中的概率,目標(biāo)要么被摧毀,要么逃逸,不存在被部分摧毀的情況,即認(rèn)為被擊中的目標(biāo)或碎片不再具有威脅[5]。
目標(biāo)毀傷概率Kj表示在整個攔截系統(tǒng)內(nèi)針對單一威脅目標(biāo)的攔截能力, j為目標(biāo)的類型,在本文討論中,假設(shè)所有類型的攔擊概率獨(dú)立同分布。通常,攔截系統(tǒng)對目標(biāo)的殺傷至少包含3個階段。1)目標(biāo)的探測和跟蹤;2)作戰(zhàn)管理與指揮控制系統(tǒng)對各類型目標(biāo)探測傳感器(如高低軌的紅外衛(wèi)星,X波段陸基雷達(dá),合成孔徑雷達(dá)系統(tǒng))數(shù)據(jù)的融合和處理,以及指揮控制指令的傳達(dá);3)攔截彈的發(fā)射。本文將前兩個階段出現(xiàn)的各類錯誤和誤差等導(dǎo)致攔截失敗的因素統(tǒng)一在pj,t中包含,如目標(biāo)跟蹤和識別錯誤,由于數(shù)據(jù)融合過程中出現(xiàn)誤差導(dǎo)致的攔截失敗,指揮控制信息傳遞過程中的丟失和延遲導(dǎo)致攔截失敗等,廣義上導(dǎo)彈攔截全過程的跟蹤概率可表示為
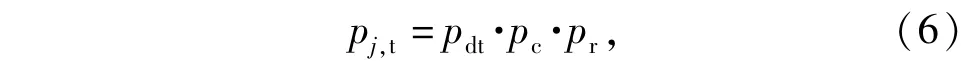
式中:pdt表示反導(dǎo)預(yù)警信息系統(tǒng)能夠提供滿足攔截彈制導(dǎo)要求的探測和跟蹤精度的概率;pc表示目標(biāo)被識別為彈頭概率,對彈頭來說識別概率即為pww,對誘餌來說識別概率即為pdw;pr表示整個反導(dǎo)系統(tǒng)系統(tǒng)的可靠性。目標(biāo)毀傷概率Kj可表示為
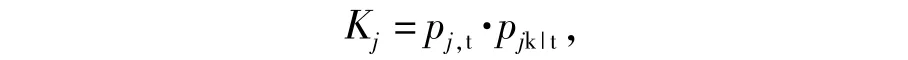
式中:pjk|t為目標(biāo)類型j的導(dǎo)彈威脅在被正確跟蹤前提下被摧毀的條件概率,其又可以表示為

其中kji表示攔截彈對目標(biāo)類型為j的目標(biāo)第i次的單發(fā)毀傷概率(SSPK),且之前的i-1次均攔截失敗,直到第n枚攔截彈才攔截成功。理想情況下對于類型為j的導(dǎo)彈威脅的單發(fā)命中概率為kj且攔截彈的直接攔截概率相互獨(dú)立[7],則(7)式可以簡化為

由(4)式和(8)式,要滿足所有的導(dǎo)彈威脅都被攔截,則針對每個威脅目標(biāo)所需發(fā)射攔截彈的數(shù)量n應(yīng)為
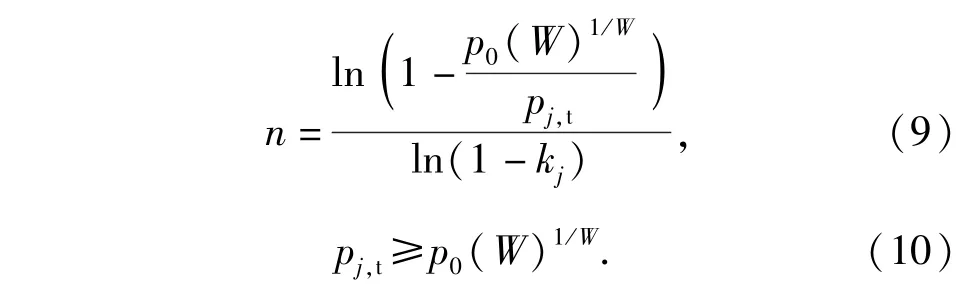
不失一般性,在后文的討論中,略去表示目標(biāo)類型的下角標(biāo)j.(9)式中所需每目標(biāo)攔截彈的數(shù)量n必須向上取整。顯然,為了保證(9)式有意義,pt≥p0(W)1/ W.如上所述,pt通常由反導(dǎo)系統(tǒng)各分系統(tǒng)固有的各項(xiàng)戰(zhàn)術(shù)技術(shù)指標(biāo)綜合決定,因此在規(guī)劃系統(tǒng)綜合攔截指標(biāo)時,必須考慮攔截系統(tǒng)的實(shí)際能力,在合理的范圍內(nèi)要求p0(W)和W.
3 齊射方式和連續(xù)發(fā)射方式
3.1攔截彈齊射方式
假設(shè)威脅目標(biāo)中識別出的彈頭數(shù)量為W*,若采用齊射方式進(jìn)行攔截,為了滿足高層指標(biāo)p0(W),發(fā)射的攔截彈數(shù)量IB應(yīng)該為
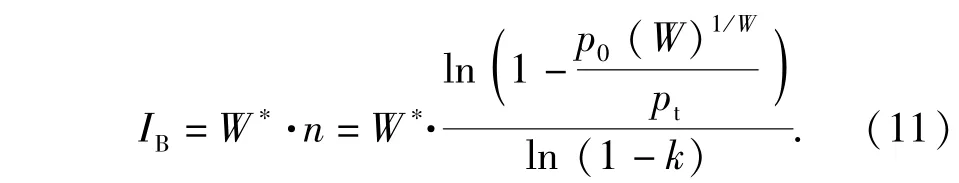
圖1所示為齊射模型下,攔截彈數(shù)量隨廣義跟蹤能力pt和攔截彈單發(fā)命中概率的變化情況。攔截指標(biāo)為:60%的概率能夠全部攔截包含10枚彈頭的彈道導(dǎo)彈威脅,即p0(W) = 0.6.按照(10)式,當(dāng)pt<0.95時,無論發(fā)射多少枚攔截彈,都不能滿足攔截指標(biāo)。在Oχy平面上的依次為所需攔截彈數(shù)量50、100、200、250、300、450的等高線,由于每目標(biāo)所需攔截彈的數(shù)量n向上取整,所以,IB應(yīng)向上取整為n的整數(shù)倍。例如對于SSPK 0.4≤k≤0.5,pt≤0.97,IB應(yīng)取整為100,即每目標(biāo)所需的攔截彈數(shù)量為10.若攔截目標(biāo)中包含誘餌,所需的攔截彈數(shù)量應(yīng)乘以系數(shù)W*/ W.
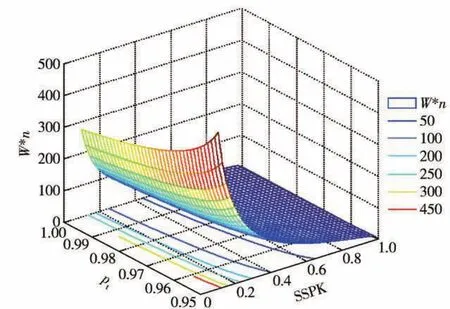
圖1 攔截指標(biāo)為p0(W) =0.6時齊射模式下攔截彈數(shù)量IBvs.pt、SSPKFig.1 Interceptor number IBvs.ptand SSPK for p0(W) = 0.6 at the mode of salvo fire
3.2攔截彈連續(xù)方式
相比于齊射攔截,連續(xù)發(fā)射方式下,后續(xù)發(fā)射的攔截彈針對的僅僅只是在上一次打擊中逃逸的目標(biāo),在同一攔截指標(biāo)下,減少了所需的攔截彈數(shù)量,降低了攔截站對常備武器庫數(shù)量的要求,特別是對于移動平臺來說,攜帶較少的攔截彈,機(jī)動能力大大增強(qiáng)。但是,由于彈道導(dǎo)彈飛行速度快,在同一攔截站出現(xiàn)的攔截時間窗口短,通常不具備發(fā)射多輪攔截彈的機(jī)會。
這里以兩輪攔截為例討論,若s表示第一輪攔截窗口發(fā)射的攔截彈數(shù)量,則所需的攔截彈總數(shù)IL為
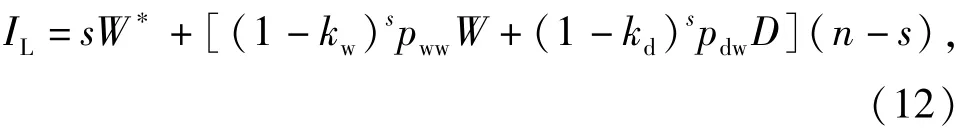
式中:n為按照(9)式計算的需發(fā)射的攔截彈數(shù)量。若定義反導(dǎo)系統(tǒng)識別目標(biāo)威脅比率:
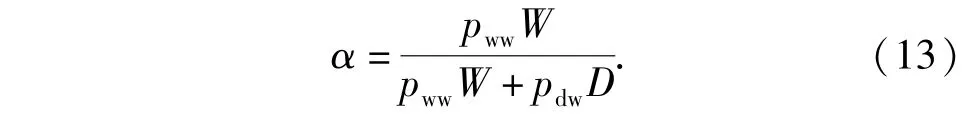
則(12)式可被重寫為
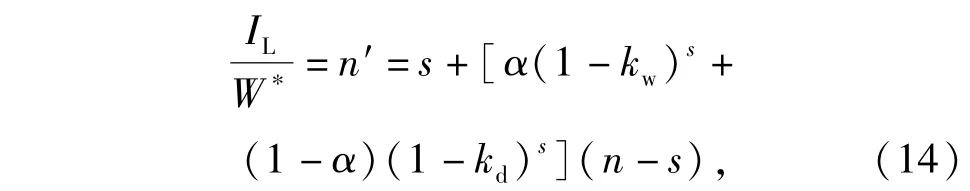
式中:n'表示在兩層攔截方式下平均每個目標(biāo)所需攔截彈數(shù)量。
圖2所示為相同攔截指標(biāo)下,采用齊射方式攔截和連續(xù)發(fā)射方式攔截時所需攔截彈數(shù)量的對比。由圖2(a)可見,兩種攔截方式,所需攔截彈的數(shù)量都隨攔截指標(biāo)W增加,連續(xù)發(fā)射方式下所需的攔截彈數(shù)量要明顯小于齊射模型,并且,隨著威脅目標(biāo)中誘餌數(shù)量的增加,這種趨勢更加明顯;圖2(b)同時比較攔截彈數(shù)量隨SSPK和W的變化,隨著SSPK的降低,所需攔截彈數(shù)量急劇增長,但連續(xù)發(fā)射方式仍然優(yōu)于齊射。
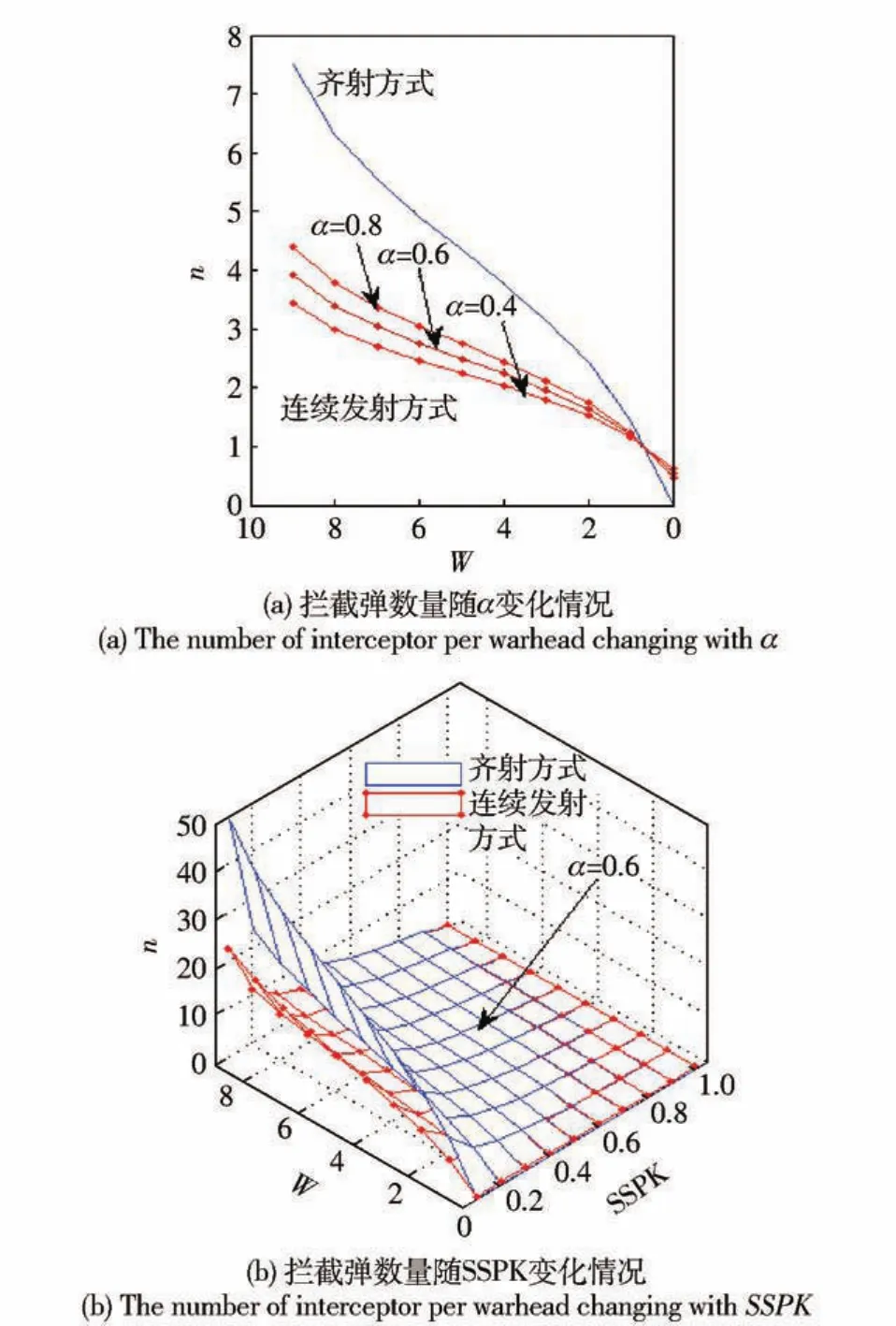
圖2 當(dāng)p0(W) =0.6時齊射方式和連續(xù)發(fā)射方式下的攔截彈數(shù)量變化情況Fig.2 Interceptor number for p0(W) =0.6 at the modes of salvo fire and string firing
盡管如此,由于彈道導(dǎo)彈飛行速度快,同一攔截站出現(xiàn)多次攔截時間的可能很低,通常采用分層防御的方式由多個攔截站依次攔截。
4 分層防御
假設(shè)3 各層防御系統(tǒng)依次對目標(biāo)進(jìn)行攔截,本層逃逸的目標(biāo)可嘗試在下層再次攔截,因此,各層防御系統(tǒng)攔截彈的使用都是采用齊射方式而不使用連續(xù)發(fā)射方式。
若每層攔截彈的SSPK獨(dú)立同分布,各層針對每目標(biāo)發(fā)射的攔擊彈數(shù)量表示為nm,m = 1,2,…, M.為了簡化分層攔截時攔截彈的部署優(yōu)化問題,假設(shè)各層的廣義跟蹤概率都為1,則第m層攔截系統(tǒng)目標(biāo)攔截概率表示為

若定義wm表示第m層出現(xiàn)的目標(biāo)的概率,則
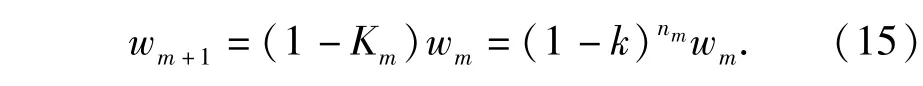
為了保證各層發(fā)射的攔截彈整體效能最優(yōu),定義平均每目標(biāo)消耗攔截彈數(shù)量EC和平均每逃逸目標(biāo)消耗攔截彈數(shù)量EE:
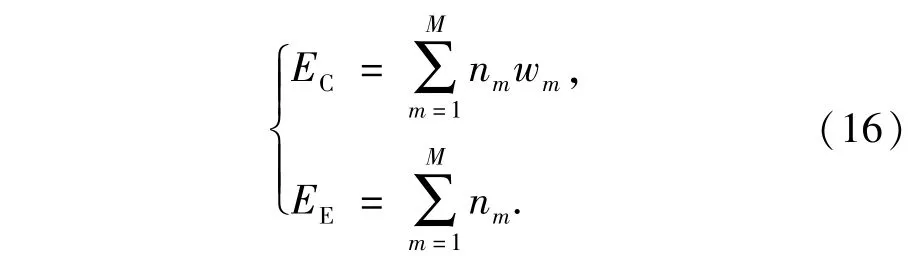
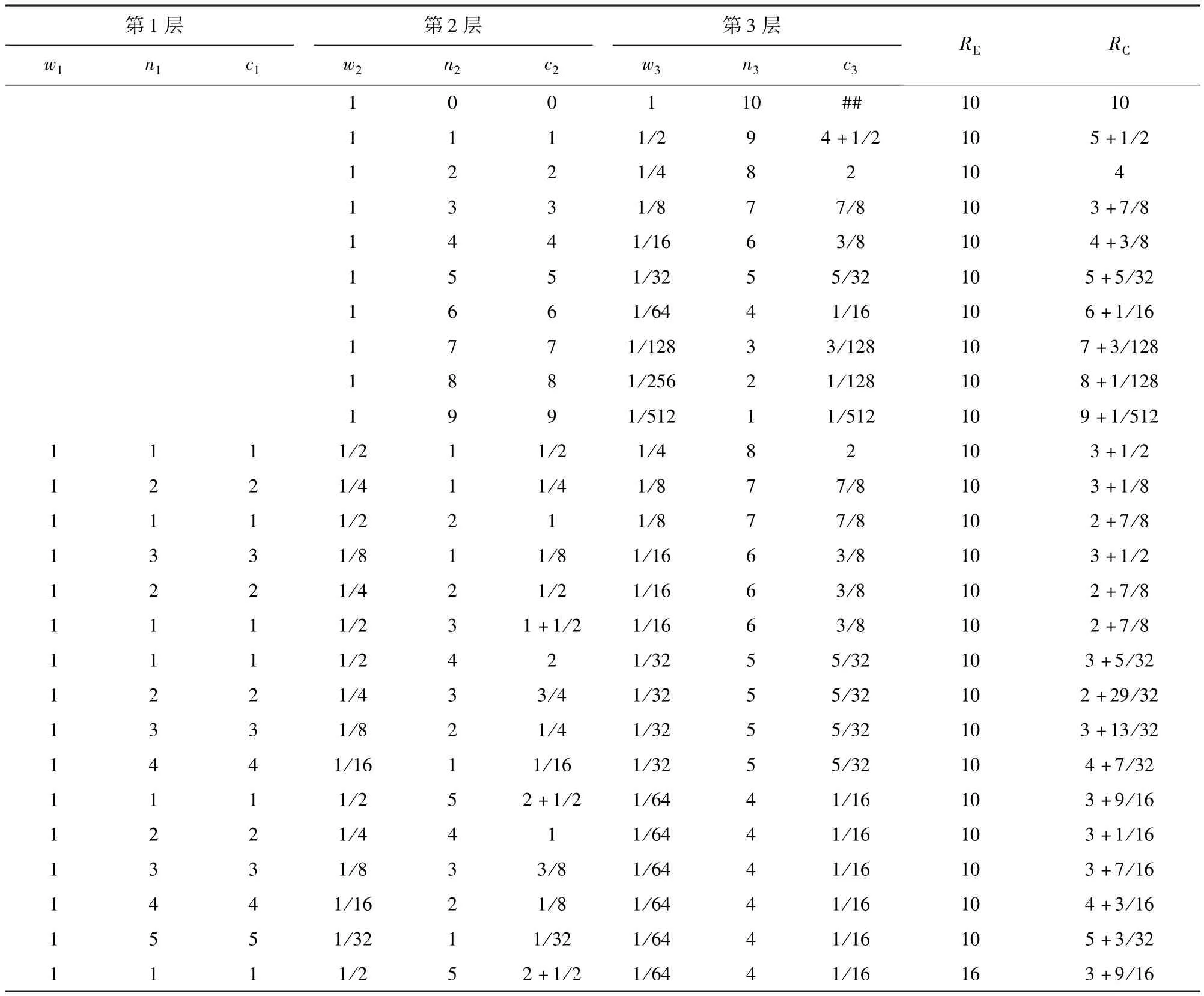
表1 EE=10和不同攔截方案下的平均每目標(biāo)攔截彈消耗數(shù)量變化情況Tab.1 The average number of consumed interceptors for EE=10 for different intercept schemes
(16)式中:平均每目標(biāo)消耗攔截彈數(shù)量度量的是攔截彈的使用效率,EC越小,概率意義下攔截彈的平均使用效率越高;平均每逃逸目標(biāo)消耗攔截數(shù)量用來度量單個目標(biāo)逃逸的可能,EE越大,概率意義下目標(biāo)逃逸的可能越小。
以3層攔截為例M≤3,攔截指標(biāo)為W = 64, p0(64) =90%;假設(shè)目標(biāo)中不存在誘餌彈,且各層的廣義跟蹤概率都為1,即pt=1;各層攔截彈SSPK獨(dú)立同分布,即k =1/2.則按照(9)式,理論上每目標(biāo)發(fā)射的攔擊但數(shù)量應(yīng)為n = 10,所以有EE=10 = n1+ n2+ n3,在此條件下,求解n1、n2和n3的值,使得EC最小。
表1列舉了2層防御和3層防御情況下,不同攔截彈分配方案對平均每目標(biāo)攔截彈消耗的變化情況,其中w1= 1,wm按照(15)式依次計算,定義cm為每層平均消耗的攔截彈數(shù)量,則有cm= wmnm, EC=Σcm.顯然最優(yōu)的攔截方案有3種組合,即n1∶n2∶n3分別為1∶2∶7、2∶2∶6和1∶3∶6.圖3為3層防御情況下,EC隨攔截方案的變化情況,其中χ軸和y軸分別表示第1層和第2層每目標(biāo)發(fā)射攔截彈的數(shù)量n1和n2,n3=10-n1- n2,與表1結(jié)論相同, 當(dāng)n1∶n2取1∶2、2∶2和1∶3時,EC最小,概率意義下攔截彈使用效率最高。
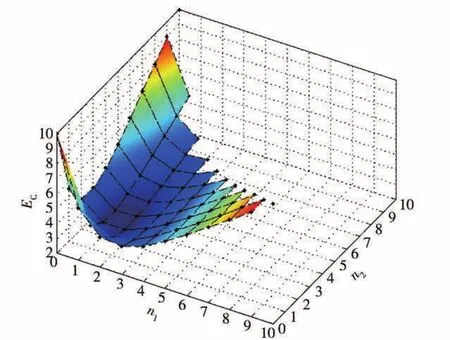
圖3 p0(64) =0.9時EC隨攔截方案變化的情況Fig.3 The values of ECfor p0(64) =0.9 for different intercept schemes
以1∶2∶7的攔截方案為例,針對來襲的64個彈頭,在第1層攔截的時候每目標(biāo)發(fā)射1枚攔截彈,在第2層攔截的時候,對剩余的目標(biāo)每目標(biāo)發(fā)射2枚攔截彈,在第3層攔截的時候,再對每目標(biāo)發(fā)射7枚攔截彈。在這種攔截方案下,目標(biāo)的逃逸概率為(1-1 /2)10≈1-p0(64)1/64,與攔截指標(biāo)p0(64)要求一致,并且保證概率意義下,攔截彈的數(shù)量最少,平均攔截每個目標(biāo)消耗的攔截彈數(shù)量為2.875枚。
5 結(jié)論
本文從攔截彈的分配和部署的角度對反導(dǎo)系統(tǒng)的效能進(jìn)行分析,在概率模型的基礎(chǔ)上將攔截彈數(shù)量和防御指標(biāo)進(jìn)行關(guān)聯(lián),針對攔截彈的齊射發(fā)射方式和連續(xù)發(fā)射方式討論了防御指標(biāo)、系統(tǒng)跟蹤概率、攔截彈目標(biāo)毀傷概率等對攔截數(shù)量的影響。最后,定義了每目標(biāo)攔截彈消耗數(shù)量作為評價指標(biāo),在保證攔截指標(biāo)的前提下,研究了分層防御攔截方案的最優(yōu)化問題。
事實(shí)上,彈道導(dǎo)彈的防御與諸多因素密切相關(guān),本文對誘餌彈的釋放方式和攔截彈殺傷效果做了理想化假設(shè),并將目標(biāo)的探測跟蹤制導(dǎo)等一系列過程對最終攔截效果的影響用廣義跟蹤能力進(jìn)行簡化。而在實(shí)際中,這一概率與反導(dǎo)系統(tǒng)的指揮控制系統(tǒng)、各型探測裝備、火控系統(tǒng)以及人員操作水平等復(fù)雜因素相關(guān)。盡管如此,本文所采用的概率模型和攔截彈優(yōu)化的思路仍然可以為攔截方案的設(shè)計和評估提供理論依據(jù),確保攔截作戰(zhàn)整體作戰(zhàn)效能最優(yōu)。下一步的工作將進(jìn)一步考慮攔截過程中存在的多攔截站相互交接和協(xié)同等問題,建立更精細(xì)的模型,討論這些因素對攔截效能的影響。
參考文獻(xiàn)(References)
[1]Department of Defense.Ballistic missile defense review report [R].Washington, DC: Department of Defense, 2012.
[2]Obama B.National security strategy of the United States (2010) [R].Washington, DC: The White House, 2010:1-51.
[3]符俊,蔡洪,張士峰,等.航天器遠(yuǎn)程最優(yōu)攔截方法研究[J].固體火箭技術(shù), 2011, 34(6): 682-686.FU Jun,CAI Hong,ZHANG Shi-feng, et al.Research on spacecraft long-range optimal interception[J].Journal of Solid Rocket Technology,2011, 34(6): 682-686.(in Chinese)
[4]Su L, He J H, Wang J Q.Assessment for effectiveness of missilegun integrated weapon system based on FSKA model[C]∥International Conference on Electric Information and Control Engineering.Wuhan, China: IEEE, 2011: 191-195.
[5]Lape N J.Measuring the effectiveness of the conus air and missile defense C2 system[R].New York: United States Military Academy, West Point, 2011:1-80.
[6]王成思,劉明陽,宋晉敏.末段反導(dǎo)武器配系部署規(guī)劃研究[J].現(xiàn)代防御技術(shù), 2015, 43(6):87-92.WANG Cheng-si, LIU Ming-yang, SONG Jin-min.Optimal deploy of terminal segment missile defense weapon[J].Modern Defence Technology, 2015, 43(6):87-92.(in Chinese)
[7]Larson E V, Kent G A.A new methodology for assessing multilayer missile defense options[R].Santa Monica: RAND, 1994:1-66.
[8]Ender T, Leurck R F, Weaver B, et al.Systems-of-systems analysis of ballistic missile defense architecture effectiveness through surrogate modeling and simulation [J].IEEE Systems Journal, 2010, 4(2): 156-166
[9]Wilkening D A.A simple model for calculating ballistic missile defense effectiveness [ J].Science & Global Security, 2000, 8(2): 183-215.
[10]高恩宇,劉曉坤.彈道導(dǎo)彈防御系統(tǒng)攔截概率的簡化模型[J].導(dǎo)彈與航天運(yùn)載技術(shù), 2013 (3): 35-38.GAO En-yu, LIU Xiao-kun.Simplified model for intercepting probability of ballistic missile defense system[J].Missiles and Space Vehicles, 2013(3): 35-38.(in Chinese)
[11]徐品高.點(diǎn)防空導(dǎo)彈武器系統(tǒng)攔截方案與火力分配[J].戰(zhàn)術(shù)導(dǎo)彈技術(shù), 1993(1):7-17.XU Pin-gao.Interceptor mechanism and firepower assignment for point-defense missile system [J].Tactical Missile Technology, 1993(1): 7-17.(in Chinese)
The Optimization and Evaluation of Ballistic Missile Defense System Interception Scheme Based on Probability Model
GAO Ang1, HU Yan-su2
(1.School of Electronics and Information, Northwestern Polytechnical University,Xi’an 710072,Shaanxi, China 2.School of Electronic and Control Engineering, Chang’an University,Xi’an 710064,Shaanxi, China)
Abstract:How to design and deploy the interception schemes to meet the specific high-level defense objective is discussed.A correlation between defense objective and the number of interceptors is established based on Bernoulli trial model, and the effects of system generalized tracking ability and single-shot kill probability on the number of interceptors are analyzed as well.the factors, such as high-level defense objective, target number and single-shot kill probability, that affect consumption of interceptors at the modes of salvo fire and string firing are discussed.At the premise of defense objective, the interceptor allocation in a layered defense is modeled as an optimization problem.The average number of consumed interceptors can be minimized by optimizing the quantity of interceptors against the targets in each defense layer.
Key words:system assessment and feasibility analysis; ballistic missile defense system; Bernoulli model;interception
作者簡介:高昂(1984—),男,講師,博士。E-mail: gaoang@ nwpu.edu.cn;胡延蘇(1985—),女,講師,博士。E-mail: huyansu@163.com
基金項(xiàng)目:國家自然科學(xué)基金項(xiàng)目(61203233)
收稿日期:2015-08-05
DOI:10.3969/ j.issn.1000-1093.2016.02.026
中圖分類號:V19
文獻(xiàn)標(biāo)志碼:A
文章編號:1000-1093(2016)02-0379-06

