內爆加載金屬界面不穩定性的數值分析*

郝鵬程,馮其京,胡曉棉,2

(1.北京應用物理與計算數學研究所，北京 100094;2.北京應用物理與計算數學研究所計算物理國家重點實驗室，北京 100088;3.中國工程物理研究院研究生部，北京 100088)

內爆加載金屬界面不穩定性的數值分析*

郝鵬程1,2,3,馮其京1,胡曉棉1,2

(1.北京應用物理與計算數學研究所，北京 100094;2.北京應用物理與計算數學研究所計算物理國家重點實驗室，北京 100088;3.中國工程物理研究院研究生部，北京 100088)

采用自行研制的多介質彈塑性流體力學歐拉程序，對柱形內爆加載金屬界面不穩定性進行了數值研究，數值模擬結果與文獻實驗數據吻合較好。數值結果表明：材料強度對界面不穩定性發展有不可忽略的抑制作用；材料屈服強度對較高模數不穩定性增長的抑制較強，而剪切模量對不穩定性發展的影響相似但敏感性相對較弱；金屬界面不穩定性增長存在最不穩定模數，最不穩定模數隨屈服強度增加而減小，并近似與屈服強度的對數呈線性關系；隨著殼的厚度減小，擾動增長加快。

流體力學；界面不穩定性；彈塑性；內爆；材料參數

輕介質支撐或者加速重介質，介質界面會發生Rayleigh-Taylor不穩定性(RTI)，不穩定性誘發界面擾動增長，重介質形成尖釘侵入輕介質，輕介質氣泡進入重介質；而當激波掠過介質界面，會發生Richtmyer-Meshkov不穩定性(RMI)，RMI的發展結果往往成為RTI發展的初始條件[1-2]。不穩定性現象廣泛存在于天體物理、地球物理、慣性約束聚變(ICF)等領域。無黏流體的不穩定性增長最快，存在多種制穩機制，比如黏性、表面張力、密度梯度、材料強度、燒蝕等。對于彈塑性介質，J.W.Miles[3]給出了無限厚彈性介質RT不穩定性增長的截止波長；D.C.Drucker[4]給出了彈性介質RT不穩定性增長的截止振幅；A.I.Lebedev等[5]給出了有限厚彈性介質RT不穩定性發展截止擾動振幅與波長、厚度之間的關系。J.F.Barnes等[6]通過爆轟加載鋁片實驗，確認了金屬界面RT不穩定性的發展存在截止波長和振幅。J.W.Swegle等[7]對彈塑性介質RTI進行了充分的理論分析以及數值模擬工作，認為彈塑性介質界面不穩定性發展不僅依賴于擾動波長、振幅、介質厚度，還與壓力加載方式等因素相關。K.Mikaelian[8]提出黏性流體RMI的指數增長模型，J.D.Colvin等[9]將塑性介質應力與黏性流體類比，分析彈塑性介質的界面不穩定性，A.R.Piriz等[1-2]對彈塑性介質RTI以及RMI進行了有意義的理論解析探索。界面不穩定性是實驗研究材料彈塑性參數及其動態響應特性的重要手段之一[10-11]。內爆過程中界面不穩定性是重要的研究方向，是影響ICF靶丸壓縮、點火狀態的重要因素之一。V.Frachet等[12]通過套筒實驗，研究了柱形內爆加載下流體以及金屬介質界面不穩定性，H.S.Park等[13]在更高壓力、應變率下研究金了屬界面不穩定性。劉軍等[14]對文獻[12]中的實驗進行了數值模擬。

本文中，使用自行研制的多介質彈塑性流體力學歐拉程序(MEPH2Y)[15]，對柱形內爆加載金屬界面不穩定性進行數值模擬，分析影響金屬界面不穩定性發展的因素，探索金屬界面不穩定的發展規律。

1 計算方法

1.1 計算模型

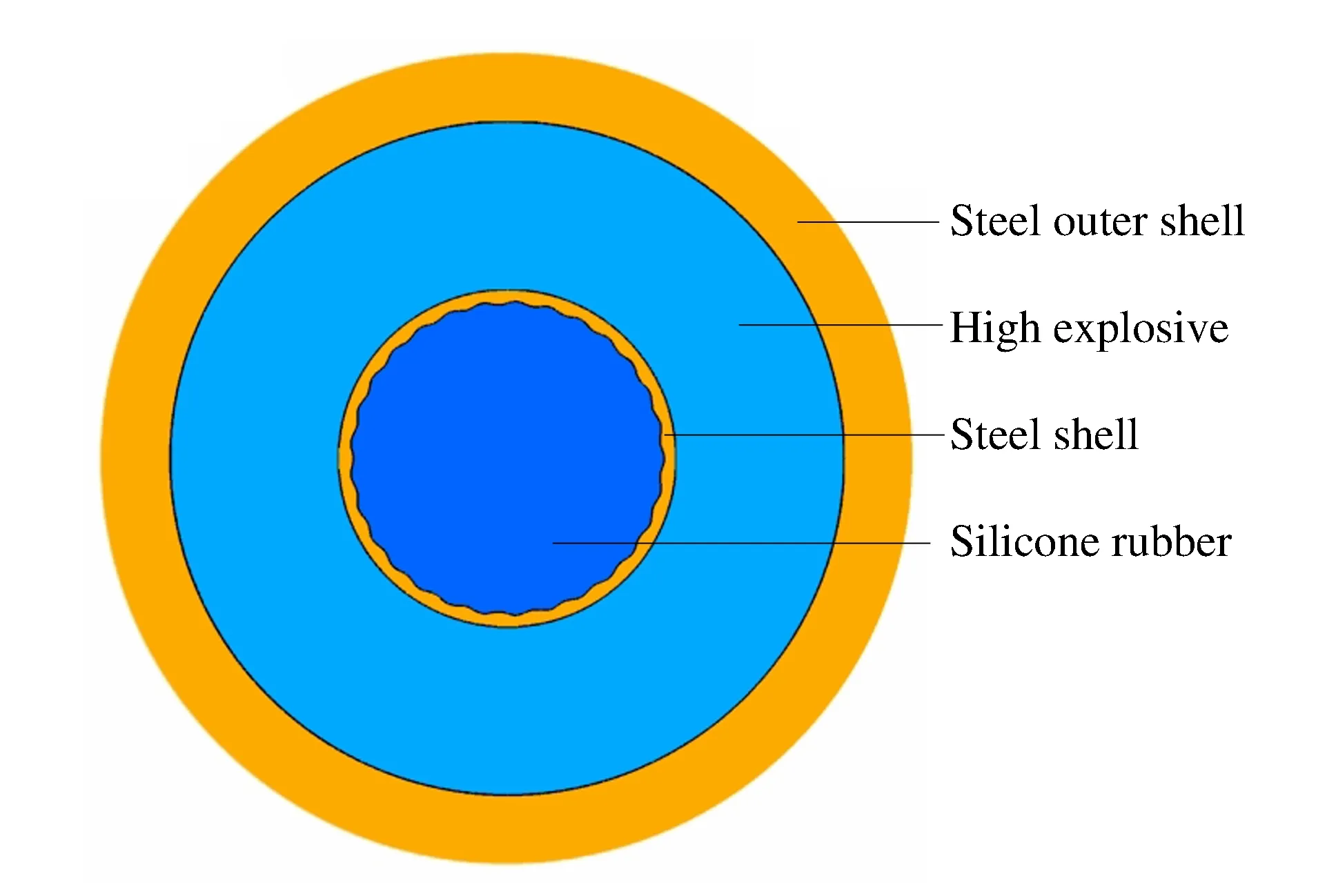
圖1 柱形內爆計算模型Fig.1 Computational model in cylindrical implosion

采用與文獻[12]實驗相似的幾何構型(如圖1所示)，外層為鋼殼，向中心分別為高能炸藥、薄鋼殼、硅橡膠。鋼外殼，厚度2 cm；炸藥，外壁半徑10 cm，厚5 cm，從外壁面起爆爆炸藥；內層鋼殼，厚4 mm，在內層鋼殼的內壁刻振幅0.5 mm的正弦曲線。

1.2 數值方法

在界面不穩定性問題中存在界面大變形現象，因此，在數值模擬中采用自行研制的歐拉程序。所使用的多介質彈塑性流體力學程序(MEPH2Y)采用交替方向方法進行時間推進，在每個方向上進行拉氏計算，而后重映到原始網格，界面采用VOF方法重構界面。該流體力學程序能夠模擬流體和彈塑性介質，能夠用于炸藥爆轟、射流射彈形成及其侵徹過程等多介質復雜流場模擬，具有較強的解決實際工程計算問題的應用能力。

1.3 狀態方程及本構模型

金屬采用凝聚介質實用狀態方程：

式中：p為壓力，ρ為密度，c0為初始聲速，ρ0為初始密度，γ為比熱比。材料參數分別為：鋼材料，ρ0=7.8 g/cm3，c0=3.8 km/s，γ=4.075；硅橡膠，ρ0=1.1 g/cm3，c0=0.5 km/s，γ=1.6。爆轟計算中，炸藥使用CJ爆轟結合Wilkins反應率的時間起爆方式，爆轟產物采用理想氣體狀態方程。炸藥參數為：初始密度1.8 g/cm3，爆速7.5 km/s，比熱比3.0。

材料采用理想彈塑性本構模型，使用von Mises準則確定介質的彈塑性狀態，材料剪切模量G為常數，材料屈服強度Y滿足：Y=max(0,Y0(1-e/em))(Y0為初始屈服強度，em為融化能)。該本構模型中，剪切模量與狀態無關，屈服強度僅與內能相關，即僅有軟化的表現。材料本構參數分別為：鋼殼，G=83 GPa，Y0=2 GPa，em=1.3 kJ/g；硅橡膠基本為流體模型，Y0=0.01 GPa，G=0.01 GPa，em=0.1 kJ/g；炸藥為流體。

2 結果及分析

2.1 一維數值模擬結果

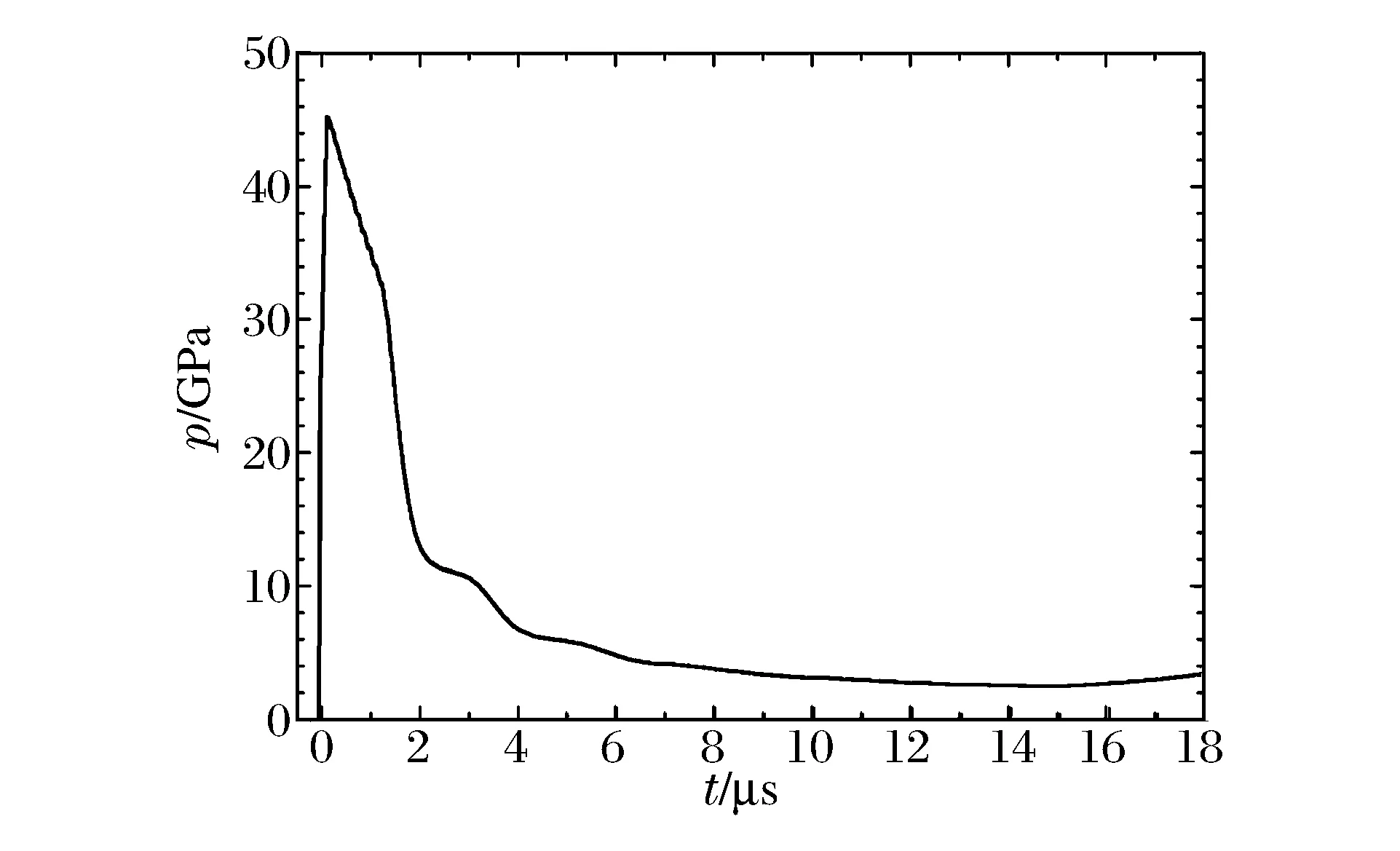
圖2 金屬殼外壁壓力Fig.2 Pressure on outer interface of metal shell

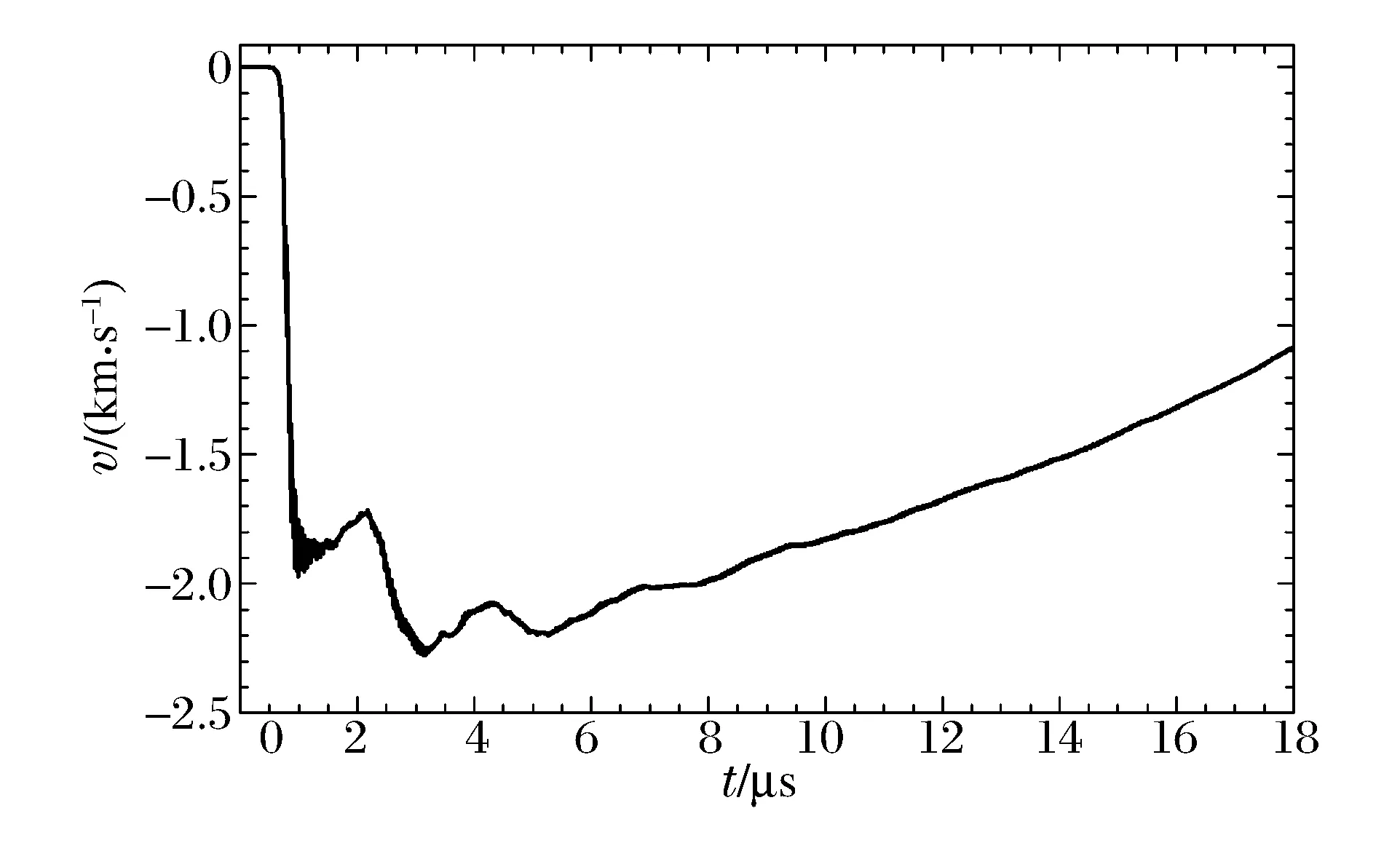
圖3 金屬殼內壁速度Fig.3 Velocity on inner interface of metal shell

通過對柱坐標一維情況的數值分析，能夠認識無擾動情況下界面運動及受力情況，為進一步分析界面不穩定性發展提供參考。數值模擬中，采用0.1 mm均勻網格。圖2為鋼殼外壁的壓力，圖3為金屬殼內的界面速度，時間原點為爆轟波到達鋼殼外壁的時刻。爆轟波在金屬外壁的壓力峰值約為45 GPa，波在金屬殼內往返，能夠清晰地看到6 μs內有3次沖擊波作用，殼層內界面得到加速，界面擾動將發生RM不穩定性。而后直到中心反射的沖擊波到達前，界面幾乎為勻減速運動，加速度指向較重的鋼殼，界面擾動的不穩定性增長將以RT不穩定性為主。

2.2 二維數值模擬結果

在二維模擬中，金屬殼的初始擾動模數n取13和29。圖4為模擬得到的擾動模數為29的殼在某時刻的界面，從中可以定性地看到，材料強度對界面不穩定性發展有較大影響。

圖5為不同初始擾動的擾動增長結果，包括純流體以及彈塑性計算。在純流體計算中，29模數的比13模數的擾動發展快，這與流體的擾動發展理論相符。對于相同模數擾動的界面，考慮彈塑性計算中的擾動比純流體計算中的擾動發展得慢，印證了材料強度是不穩定性發展的致穩因素。在彈塑性計算中，29模數的擾動未得到發展，而13模數的擾動發展雖然比純流體計算慢，但界面擾動仍然得到一定發展。這個彈塑性計算結果與實驗數據定性相符，即流體計算中發展較快的高模數在彈塑性計算中反而發展得較慢，表明金屬材料的不穩定性發展與擾動模數及材料強度均相關。另外，彈塑性計算的結果與實驗值有一定的差異，應該與計算中所使用的狀態方程、本構關系等材料特性的差異相關。

圖4 密度等值云圖(n=29)Fig.4 Density contour plot

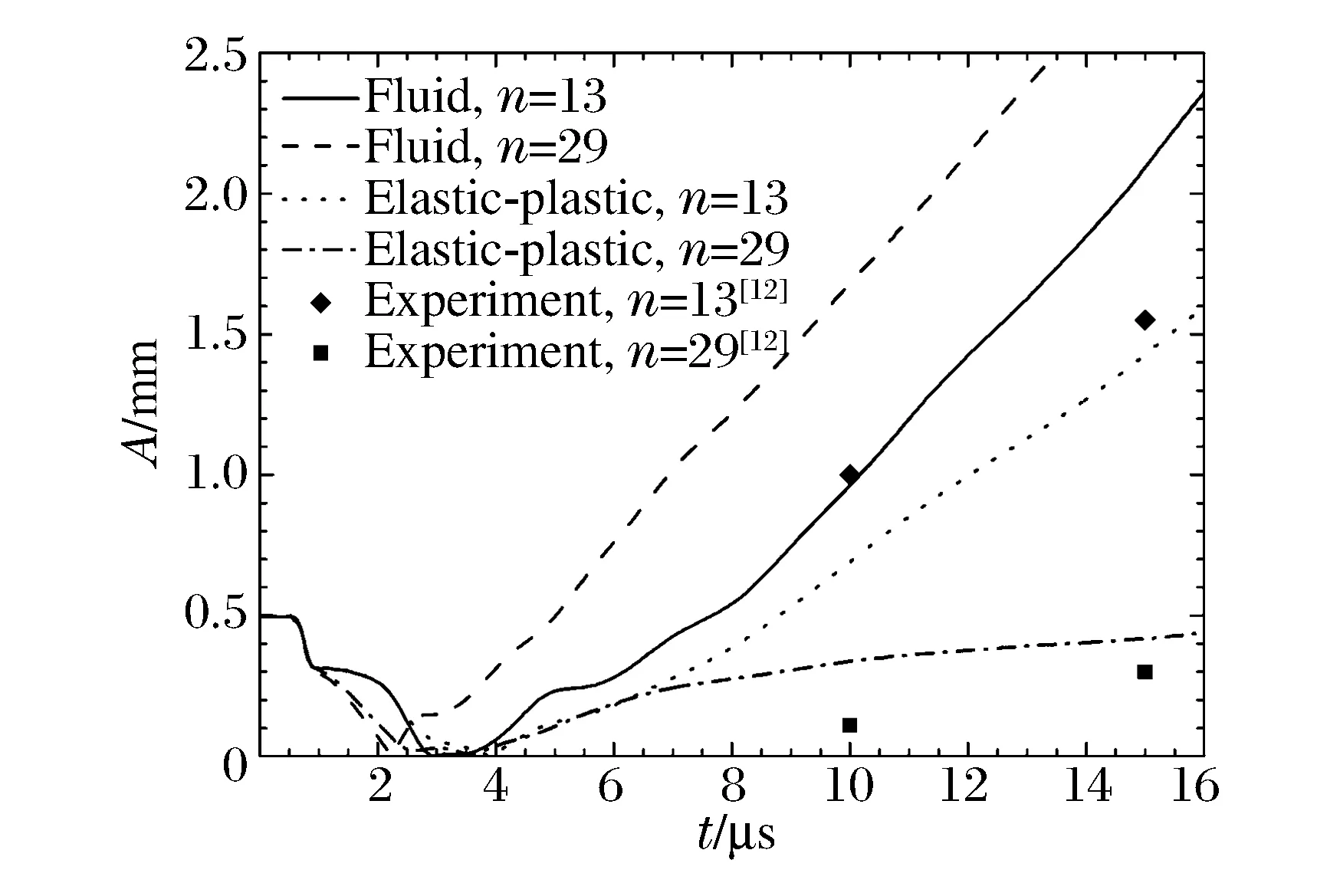
圖5 金屬界面擾動增長Fig.5 Growth of metal interfacial perturbation amplitude

2.3 材料強度與不穩定性的發展

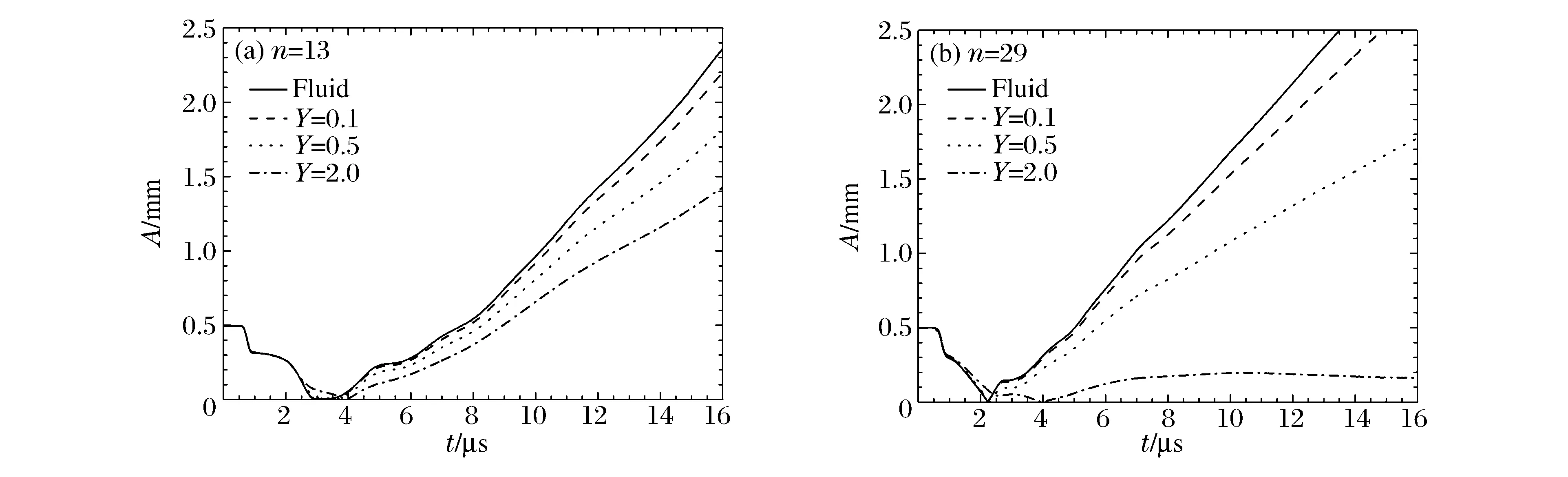
圖6 材料屈服強度對界面擾動增長的影響Fig.6 Effect of yield strength on perturbation growth

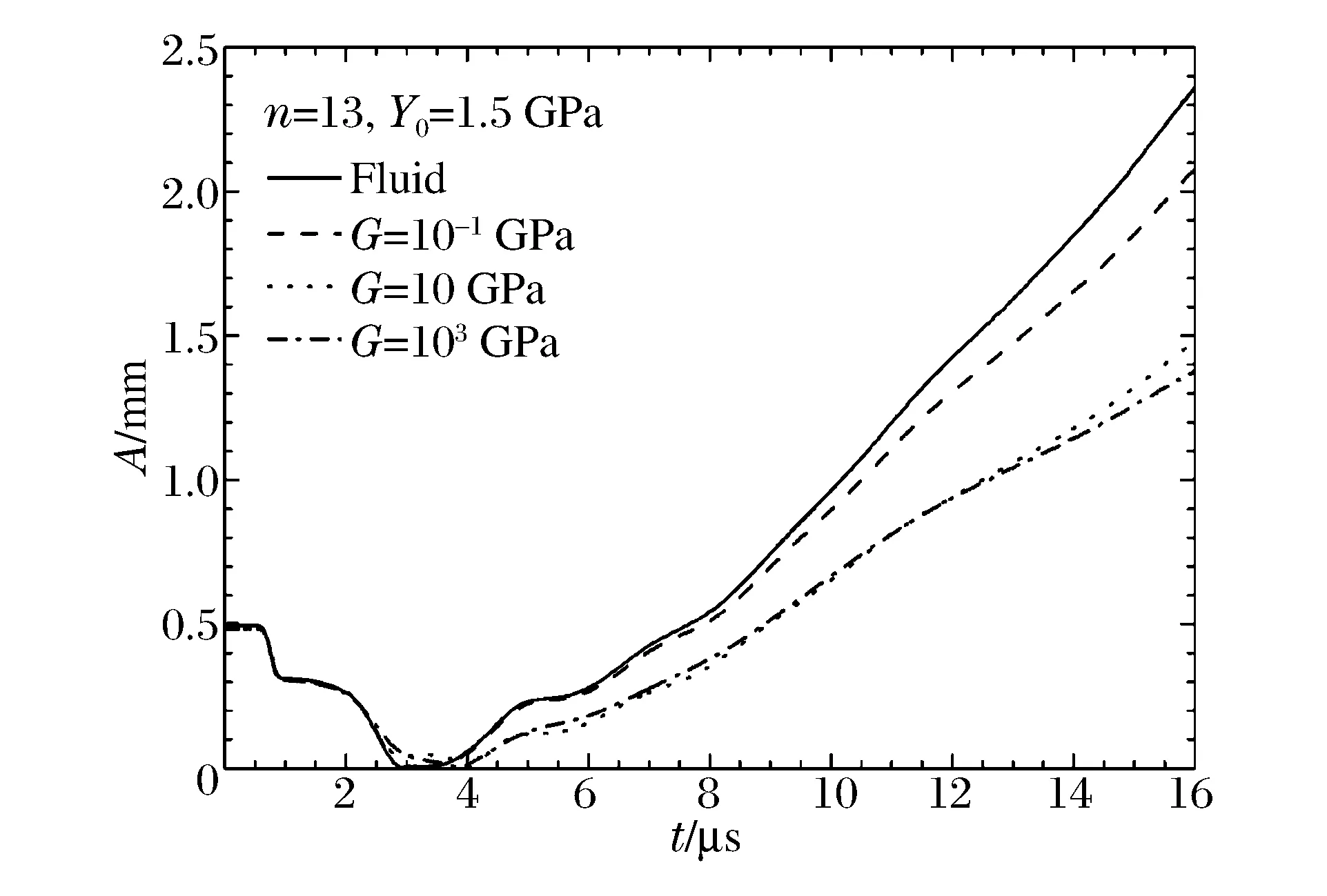
圖7 材料剪切模量對界面擾動增長的影響Fig.7 Effect of shear strength on perturbation growth

固定材料剪切模量和屈服強度中的一個，單獨調節另一個。為了排除其他因素的干擾，材料本構中屈服強度保持不變，即Y=Y0。圖6給出模數13、29在不同屈服強度下的擾動發展情況，可以看到，材料強度抑制不穩定性發展，屈服強度越大擾動發展越慢。對不同模數的擾動，屈服強度的影響不同：對于13模擾動，材料強度對擾動發展影響相對較小；而對29模擾動發展影響顯著，當Y0=2.0 GPa時，擾動甚至沒有發展。而圖7給出模數13當Y0=1.5 GPa時在不同剪切模量下的擾動發展情況，可以看出，與屈服強度相比較，剪切模量在10～1 000 GPa這樣大范圍內對不穩定性發展影響甚微。實際上，從材料屈服強度以及剪切模量在控制方程中的角色，可以理解他們對于材料所表現出的強度的貢獻。屈服強度控制材料等效偏應力張量，而剪切模量則僅控制材料偏應力張量的增長速率，因此，在較高的應變率加載下，材料的屈服強度決定了材料所體現出來的強度。另外，在擾動發展初期的RM不穩定性發展階段，內部壓強較高，材料強度相對較小，擾動增長受到材料強度的影響較弱，材料強度的作用主要體現在后期的RT不穩定性主導階段。

從圖6可知，屈服強度對不同模數的擾動影響不同。這里，以擾動模數為變量分析不穩定性發展的機制，并在給定的屈服強度下，將后期發展最快的擾動模數稱為最不穩定模數。圖8展示了不同屈服強度下不同模數的擾動隨時間增長情況，所考察的材料屈服強度Y0=0～2.0 GPa、擾動模數n=8～40。計算結果顯示：純流體計算(見圖8(a))中，最不穩性模數為最大擾動模數；中等程度的屈服強度(見圖8(b)～(c))下，隨著擾動模數增高，擾動發展速率先加快后減慢；最大的屈服強度(見圖8(d))下，最不穩定模數為最小的模數。圖9為最不穩定模數隨材料屈服強度的變化曲線，隨著屈服強度的增大，最不穩定模數單調減小，如圖9中小圖所示，最不穩定模數與屈服強度的對數近似呈線性關系：nmax≈12.2-17.0 lg(Y0/GPa)。實際上，如圖8所示，在擾動發展初期的RM不穩定性發展階段，受材料強度影響較弱，隨擾動模數的增加擾動增長速率均加快。在后期RT不穩定性發展階段，界面減速是失穩因素，在該因素作用下高模數擾動增長較快；而材料強度是致穩因素，且強度愈大對高模數擾動增長的抑制作用愈強；兩個相反因素作用的結果，使得在給定強度下擾動發展存在最不穩定模數。這個最不穩定模數下擾動增長最快，也可以理解為最危險的模數，或者說是該條件下的特征模數。

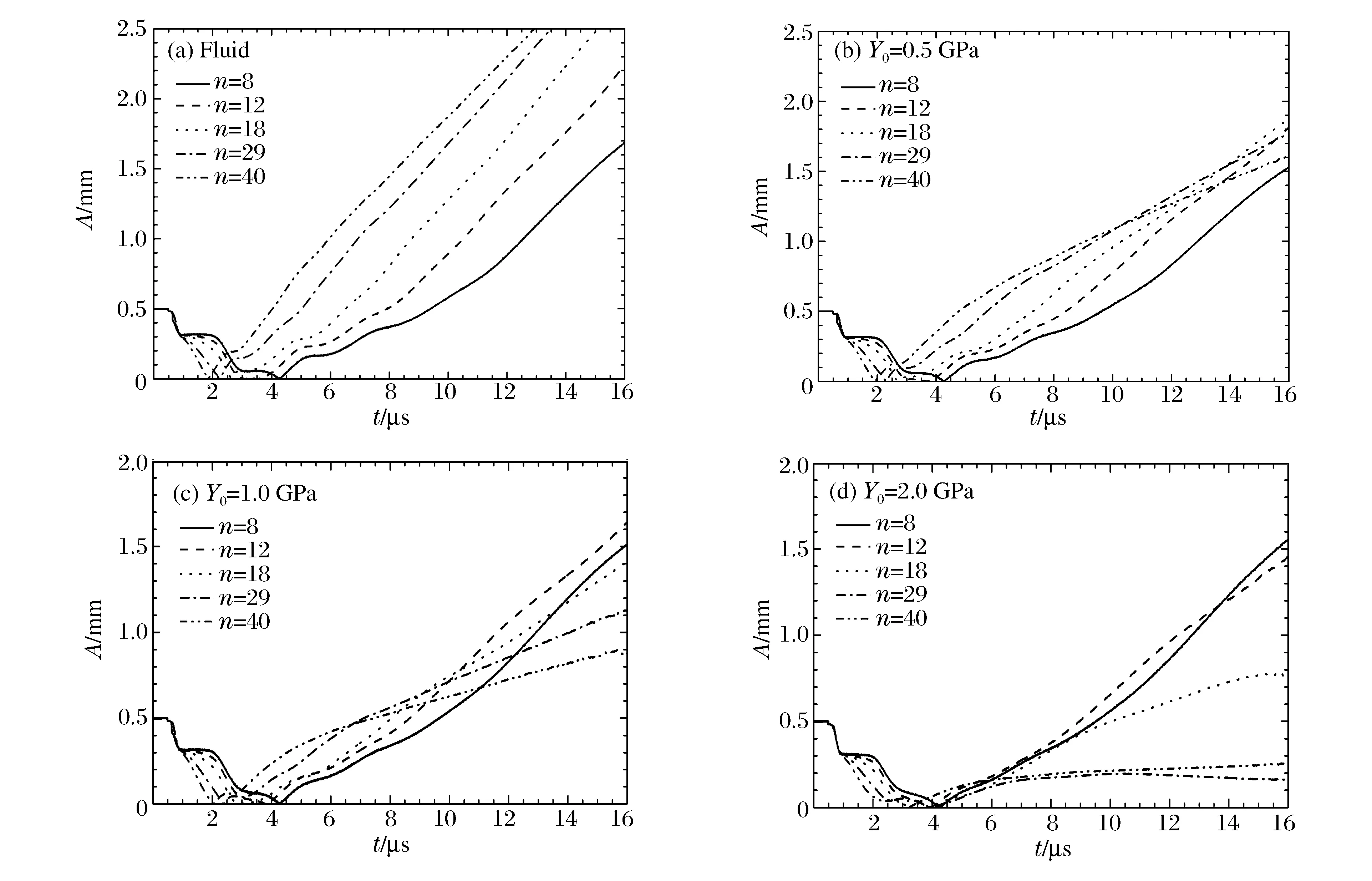
圖8 不同屈服強度下擾動模數與擾動增長的關系Fig.8 Effect of perturbation mode on perturbation growth under different yield strength

圖9 最不穩定模數與屈服強度的關系Fig.9 Relationship between yield strength and most instable mode

2.4 金屬殼厚度對不穩定性發展的影響

將金屬殼厚度4與2.5 mm的擾動發展情況進行了對比，如圖10所示。相同擾動模數的薄殼擾動發展均快于厚殼， 在這里，以Y0=0.5 GPa為例，其他強度下擾動發展情況類似。另外，如圖11所示，2.5 mm厚的最不穩定模數亦隨屈服強度的對數線性減小，nmax≈12.1-11.8 lg(Y0/GPa)，其斜率絕對值比4.0 mm厚的小，即較薄的殼其最不穩定模數隨強度的增長變化較緩。

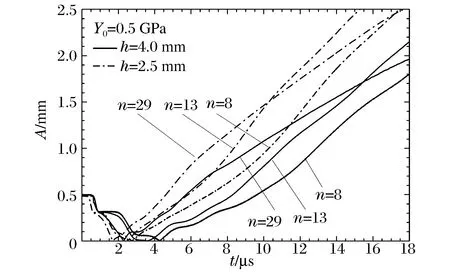
圖10 不同金屬殼厚度下的擾動增長Fig.10 Effect of shell thickness on perturbation growth

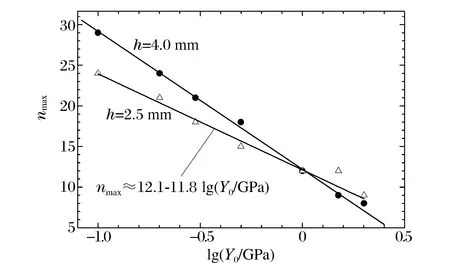
圖11 不同金屬殼厚度下最不穩定模數與屈服強度的關系Fig.11 Relationship between yield strength and most instable mode with different shell thicknesses

3 結 論

利用自行研制的彈塑性流體力學的歐拉程序，對柱形內爆加載下金屬界面不穩定開展了數值研究，結果表明本文的計算結果與文獻實驗結果吻合較好，進而研究了材料參數對于內爆加載金屬界面不穩定發展的影響規律。

對于內爆加載下金屬界面不穩定問題，殼體擾動模數、材料強度對界面不穩定性發展均有影響。對于純流體，擾動模數越高不穩定發展越快；材料強度對界面不穩定性發展有不可忽略的抑制作用，材料屈服強度對高模數不穩定增長的抑制作用較大，而材料剪切模量對不穩定性發展的影響相對較弱；對于相同擾動的金屬殼，存在最不穩定模數，且該模數隨材料屈服強度的增加而減小，近似與屈服強度的對數呈線性關系；隨著殼的厚度減小，擾動增長加快。

感謝秦承森研究員的建設性討論。

[1] Piriz A R, Lopez Cela J J, Tahir N A, et al. Richtmyer-Meshkov instability in elastic-plastic media[J]. Physical Review E, 2008,78(5):056401.

[2] Piriz A R, Lopez Cela J J, Tahir N A. Linear analysis of incompressible Rayleigh-Taylor instability in solids[J]. Physical Review E, 2009,80(4):046305.

[3] Miles J W. Taylor instability of a flat plate[R]. San Diego: General Dynamics, GAMD-7335, 1966.

[4] Drucker D C. “Taylor instability” of the surface of an elastic-plastic plate[C]∥Nemat-Nasser C. Mechanics Today, Vol. 5. New York: Pergamon Press, 1980:37-47.

[5] Lebedev A I, Nizovtsev P N, Rayevsky V A. Rayleigh-Taylor instability in solids[C]∥4th International Workshop on the Physics of Compressible Turbulent Mixing (IWPCTM). Cambridge, England, 1993.

[6] Barnes J F, Blewett P J, McQueen R G, et al. Taylor instability in solids[J]. Journal of Applied Physics, 1974,45(2):727-732.

[7] Swegle J W, Robinson A C. Acceleration instability in elastic-plastic solids. I. Numerical simulations of plate acceleration[J]. Journal of Applied Physics, 1989,66(7):2838-2858.

[8] Mikaelian K. Effect of viscosity on Rayleigh-Taylor and Richtmyer-Meshkov instabilities[J]. Physical Review E, 1993,47(1):375-383.

[9] Colvin J D, Legrand M, Remington B A, et al. A model for instability growth in accelerated solid metals[J]. Journal of Applied Physics, 2003,93(9):5287-5301.

[10] Atchison W L, Zocher M A, Kaul A M. Studies of material constitutive behavior using perturbation growth in explosive and magnetically driven liner systems[J]. Russian Journal of Physical Chemistry B, 2008,2(3):387-401.

[11] Dimonte G, Terrones G, Cheme F J, et al. Use of the Richtmyer-Meshkov instability to infer yield stress at high-energy density[J]. Physical Review Letters, 2011,107(26):264502.

[12] Frachet V, Geleznikoff F, Guix R, et al. Rayleigh Taylor instability in cylindrical configuration[C]∥2nd International Workshop on the Physics of Compressible Turbulent Mixing (IWPCTM). Pleasanton, CA, 1989.

[13] Park H S, Lorenz K T, Cavallo R M, et al. Viscous Rayleigh-Taylor instability experiments at high pressure and strain rate[J]. Physical Review Letters, 2010,104(13):135504.

[14] 劉軍，馮其京，周海兵.柱面內爆驅動金屬界面不穩定性的數值模擬研究[J].物理學報,2014,63(15):155201. Liu Jun, Feng Qijing, Zhou Haibing. Simulation study of interface instability in metals driven by cylindrical implosion[J]. Acta Physica Sinica, 2014,63(15):155201.

[15] 馮其京，郝鵬程，杭義洪，等.聚能裝藥的歐拉數值模擬[J].爆炸與沖擊,2008,28(2):138-143. Feng Qijing, Hao Pengcheng, Hang Yihong, et al. Eulerian numerical simulation of a shaped charge[J]. Explosion and Shock Waves, 2008,28(2):138-143.

(責任編輯 丁 峰)

A numerical study of the instability of the metal shell in the implosion

Hao Pengcheng1,2,3, Feng Qijing1, Hu Xiaomian1,2

(1.InstituteofAppliedPhysicsandComputationalMathematics,Beijing100094,China;2.NationalKeyLaboratoryofComputationalPhysics,InstituteofAppliedPhysicsandComputationalMathematics,Beijing100088,China;3.GraduateSchool,ChinaAcademyofEngineeringPhysics,Beijing100088,China)

In this work the instability of the metal shell in the cylindrical implosion was studied numerically using a multi-component elastic-plastic hydrodynamic Eulerian code. Agreeing with those of the experiments, the numerical results show that the material strength restrains the growth of the interfacial perturbation with an effect not to be overlooked. The material yield strength has an obvious restraining effect on the higher mode of perturbation, while that of the shear module is similar but less sensitive. There exists a most instable mode number, which decreases as the yield strength increases and is approximately linear with the logarithm of the yield strength, and the perturbation grows faster as the shell grows thinner.

fluid mechanics; interfacial instability; elastic-plastic simulation; implosion; material parameters

10.11883/1001-1455(2016)06-0739-06

2015-04-30； < class="emphasis_bold">修回日期：2015-08-17

2015-08-17

國家自然科學基金項目(11402029,11372052,11371069,U1430235)； 中國工程物理研究院科學技術發展基金項目(2015B0101021)

郝鵬程(1980— )，男，博士研究生，副研究員,hao_pengcheng@iapcm.ac.cn。

O357.41 <國標學科代碼：1302531 class="emphasis_bold"> 國標學科代碼：1302531 文獻標志碼：A國標學科代碼：1302531

A