巧用極限法解決“載去相同高度”壓強問題（上）

在學習物理時，極限分析法是比較難運用的一種方法，尤其是解壓強問題，同學們往往難以把握極限分析法解答問題的適用范圍。在解壓強類的問題時，首先需要抓住的是題干中的變量以及變量的約束范圍，然后根據壓強定律去規范出變量的變化范圍，最后再利用極限分析法去分析，這樣就能快速得出答案了。下面將結合幾道例題來與同學們一起探討如何運用極限分析法解決“截去相同高度”的壓強問題。

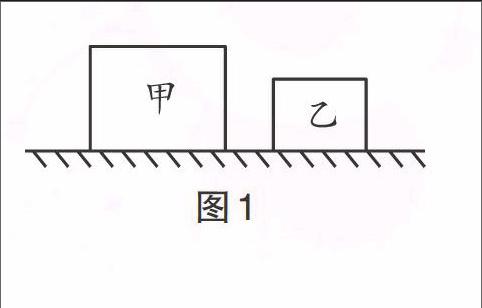
例1 如圖1所示，甲、乙兩個均勻實心的正方體分別放置在水平地面上，且它們各自對地面的壓強相等。若分別在兩個正方體的上部，沿水平方向截去相同高度后，則甲、乙的剩余部分對地面的壓強p的大小關系為（ ）。

A. [p甲p乙] C. [p甲=p乙] D. 無法確定

解析：這道題我們先用常規方法來解。依據“需截去相同高度”，則考慮高度h與壓強p的關系，可選用公式[p=ρ固gh]求解壓強問題，進一步審題可知，題意滿足該關系式的應用條件。設原來甲、乙對地面的壓強分別為[p′甲]、[p′乙]，高度為[h′甲]、[h′乙]，截去相同高度后，甲、乙對地面的壓強分別為[p甲]、[p乙]，已知條件：[p′甲=ρ甲gh′甲=p′乙=ρ乙gh′乙]，其中[h′甲>h′乙]，則[ρ甲<ρ乙]（條件1）。截去相同高度[Δh]后，因[h′甲>h′乙]，所以[h甲=h′甲-Δh>h乙=h′乙-Δh]，那么，

[p甲=ρ甲gh甲=ρ甲gh′甲-Δh=p′甲-ρ甲gΔh]——①式，

[p乙=ρ乙gh乙=ρ乙gh′乙-Δh=p′乙-ρ乙gΔh]——②式。

現在比較截去[Δh]后壓強[p甲與p乙]的大小關系，只需將①式[-]②式，即有[p甲-p乙=（p′甲-p′乙）+ρ乙-ρ甲gΔh]，其中[p′甲-p′乙=0]，根據條件1，可知[ρ乙-ρ甲gΔh>0]，所以[p甲-p乙>0]，即[p甲>p乙]。故答案選B。

從上面的解答過程可以看出，用常規方法計算較為繁瑣，很容易出錯，我們不妨試試用極限法來解決這道題。

因“沿水平方向截去相同高度[Δh]”，可以假設題設是以[Δh=h乙]去截，使得高度較小的物體截完之后高度為0，則容易判斷剩余部分，[h甲>0]，[h乙=0]。那么，意味著只有甲剩余，乙則沒有了，自然可以得出結果：[p甲>p乙]。

【小結】根據題意，截去相同高度[Δh]，[Δh]值不定，所以截多截少對問題的結果并不產生影響，因而索性認為它截去的高度正好將高度小的物體截完，如此一來，結果一目了然。這就是極限法在這道題的運用。

例2 甲、乙、丙三個實心正方體放在水平地面上，它們對地面的壓強關系是[p甲0>p乙0>p丙0]。若在三個正方體的上部，沿水平方向分別截去相同高度后，剩余部分對水平地面的壓強關系是[p甲=p乙=p丙]，則三個實心正方體的密度大小關系是（ ）。

A. [ρ甲>ρ乙>ρ丙] B. [ρ乙>ρ甲>ρ丙] C. [ρ丙>ρ乙>ρ甲] D. [ρ甲>ρ丙>ρ乙]

解析1：應用例1的極限法，根據題意，截去相同的高度，可認為是以[Δh=h最小]去截，使高度最小的物體截完，又因為截完后剩余部分對地面的壓強[p甲=p乙=p丙]，所以[Δh=h甲=h乙=h丙]，意味著甲、乙、丙原來高度一樣。又因為它們對地面的壓強關系[p甲0>p乙0>p丙0]，因存在壓強與高度關系，選用關系式[p=ρ固gh]判斷，其中[g]不變，[h]相同，壓強大的密度大，容易得出結果：[ρ甲>ρ乙>ρ丙]。故答案選A。

解析2：學完浮力一章后，由[p=ρ固gh]可知，對于某種物質而言，壓強只與高度[h]有關，從而推理知：[Δp=ρgΔh]，其中[ρ]、[Δp]、[Δh]分別指物質的密度、壓強變化量、高度差。分析題意知，滿足公式[Δp=ρgΔh]的應用條件，由[Δp=p大-p小]，且[p甲0>p乙0>p丙0]，[p甲=p乙=p丙]，則[Δp甲>Δp乙>Δp丙]。又因為[Δp=ρgΔh]，[Δh]相同，所以容易得出：[ρ甲>ρ乙>ρ丙]。

例3 兩個完全相同的圓柱形容器中，分別盛有質量相等的煤油和水，如圖2所示，已知圖中液體內[M]、[N]兩點到容器底部的距離相等，煤油的密度小于水的密度。設[M]、[N]兩點處的液體壓強分別為[pM]和[pN]，則這兩處的液體壓強大小關系是（ ）。

A. [pM]小于[pN] B. [pM]等于[pN]

C. [pM]大于[pN] D. 無法判斷

解析：根據題意，M、N兩點的壓強是由M、N上方的液體產生的，可運用公式[p=ρ液gh]，其中[ρ油<ρ水]，但[hM>hN]，使得[pM=ρ油ghM]與[pN=ρ水ghN]大小關系無法確定。

此時，我們可以采用極限法來解決。條件已知M、N兩點到容器底部的距離相等，我們可以假想M、N同時上移至（b）容器的水平面位置，此時[hM>hN=0]，再由公式[p=ρ液gh]可得，[pM=ρ油ghM>pN=0]。故答案選C。

【小結】極限法的運用，不一定是要從上往下“截”，還可以自下而上地“截”，原則是在保證“截去相同高度”的前提下進行，最終結果是要使得高度最小的部分被截完，出現極值，這樣才便于討論。

例4 如圖3所示，均勻圓柱體甲和盛有液體乙的圓柱形容器放置在水平地面上，甲、乙質量相等。現沿水平方向切去部分甲并從容器中抽取部分液體乙后，甲對地面的壓強大于乙對容器底部的壓強。若甲、乙剩余部分的體積分別是[V甲]、[V乙]，則（ ）。

A. [V甲]可能等于[V乙] B. [V甲]一定大于[V乙]

C. [V甲]可能小于[V乙] D. [V甲]一定小于[V乙]

解析：首先要明確“截”的是體積，而不是高度，另外甲是固體，乙是液體，且甲與乙“截”的部分可以不一樣，這還能用極限法嗎？我們試一試便知。

依據題目條件可知，[M甲=ρ甲V甲=M乙=ρ乙V乙]，其中[V甲>V乙]，可知[ρ甲<ρ乙]。題目需討論壓強與體積的關系，能建立起聯系的關系式是[p=ρgh]，且甲、乙均可用該關系式，要使得[p甲=ρ甲gh′甲>p乙=ρ乙gh′乙]，其中[ρ甲<ρ乙]，因而要求“截”完后[h′甲>h′乙]，又因為[S甲>S乙]，所以剩余部分的體積[V甲=S甲h′甲>V乙=S乙h′乙]一定成立。

驗證一下，我們一步到位，假想是以[Δh=h乙]截，使得[h′甲>h′乙=0]，顯然可以使[p甲>p乙]，此時[V甲>V乙]，得證。故答案選B。

【小結】“截”體積問題，我們也可以轉化為“截”高度問題，再巧妙的運用極限法，使得解答過程清晰明了。

不過，極限分析法并不是萬能的，比如截“質量”問題并不適合采用極限法。這個內容我們下期再來分析。