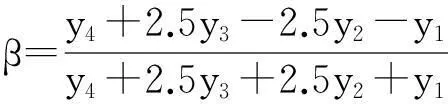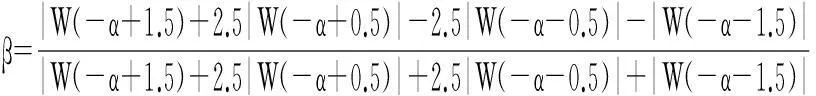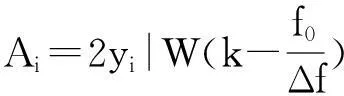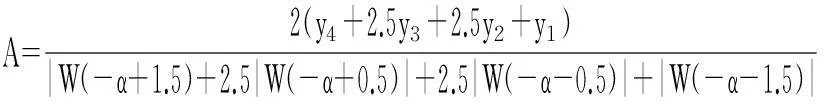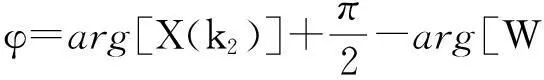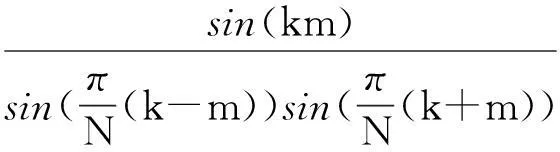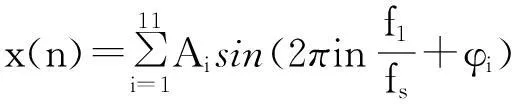一種基于Hamming自乘法窗函數和四插值的諧波分析方法

張俊敏，劉宗方，陳　勉

(中南民族大學 計算機科學學院，武漢 430074)

?

一種基于Hamming自乘法窗函數和四插值的諧波分析方法

張俊敏，劉宗方，陳勉

(中南民族大學 計算機科學學院，武漢 430074)

摘要針對諧波分析過程中常規窗函數存在精度不足的問題，提出了一種自乘法窗函數的構造方法，并以Hamming窗函數為例構造出1-9階乘法窗函數，將這些窗函數應用于四譜線插值諧波分析方法中，仿真實驗表明：構造出的自乘法窗函數相對于常規窗函數，在進行插值諧波分析中具有更高的準確度.工程實踐中可根據精度需要選擇所構造的窗函數階次.

關鍵詞諧波分析；自乘法窗函數；漢明窗；四插值

A Harmonic Analysis Method Based on Hamming Self-Multiplication Window Functions and Four-Spectrum-Line-Interpolation

ZhangJunmin,LiuZongfang,ChenMian

(College of Computer Science, South-Central University for Nationalities, Wuhan 430074, China)

AbstractIn view of precision insufficient of the conventional window functions used in harmonic analysis, this paper introduced a construction method of self-multiplication window functions, and gave self-multiplication window functions of 1-9 orders based on Hamming window, and meanwhile verified a harmonic analysis method of four-spectrum-line-interpolation based on these multiplication window functions. The simulation experiments show that the constructed window function has a higher accuracy comparing to the conventional window function interpolation algorithm. In practical engineering, we can choose the constructed window function orders according to the needs of precision.

Keywordsharmonic analysis; self-multiplication window function; Hamming window; four-spectrum-line-interpolation

電網中非線性器件的使用帶來了諧波問題，不僅惡化了電能質量，對電網的安全穩定和經濟運行也造成較大影響[1,2].因此，對電網中諧波參數進行測量，一方面可以明確當前系統的運行狀態；另一方面對于減少諧波危害，維護電網安全穩定、高效運行是十分必要的.

諧波檢測的關鍵問題為非同步采樣下如何解決頻譜泄漏和柵欄效應，常見檢測方法主要有傅里葉變換插值算法、機器學習法、小波變換、功率譜估計、希爾伯特-黃變換.傅里葉插值算法是運用各種特殊窗函數對信號進行截斷，然后結合譜線插值 FFT進行諧波分析[3].常用窗函數，例如漢寧(Hanning)窗函數[4]、布萊克曼漢斯(Blackman-Harris)窗函數[5]、納托爾(Nuttall)窗函數[6]、萊夫文森特(Rife-Vincent)窗函數[7]在插值運算中得到應用；一系列自卷積窗函數，如三角自卷積窗函數[8]、矩形自卷積窗函數[9]、Hanning自卷積窗函數[10]等也被提出.在加窗基礎上，Wu Jing等人和牛勝鎖等人提出了三譜線修正算法[11-19]，D. Agrez[15]和龐浩[4]等人各自提出了雙譜線的修正算法.這些改進降低了頻譜泄漏和柵欄效應的影響，提高了諧波分析的準確性.

為了進一步提高加窗插值算法的精度，本文在自乘法窗函數的基礎上，構建了1-9階Hamming自乘法窗函數.計算實例表明：該算法相對于雙譜線和三譜線插值算法，具有更高的準確度.

1Hamming自乘法窗

自乘法窗函數的定義為：若干個相同窗函數進行相乘所構成的新的窗函數.乘法窗的公式為：

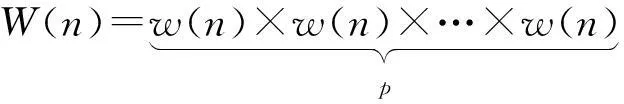
(1)

其中w(n)為基本窗函數；p為參加乘法的窗函數個數，稱為乘法窗的階數，p=1時即為原窗函數.

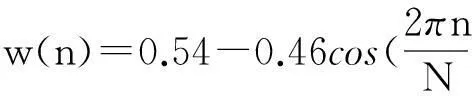
p階Hamming乘法窗的主瓣寬度(MB)為8+4p，隨著乘法階數p的增加而變寬，如表1所示.

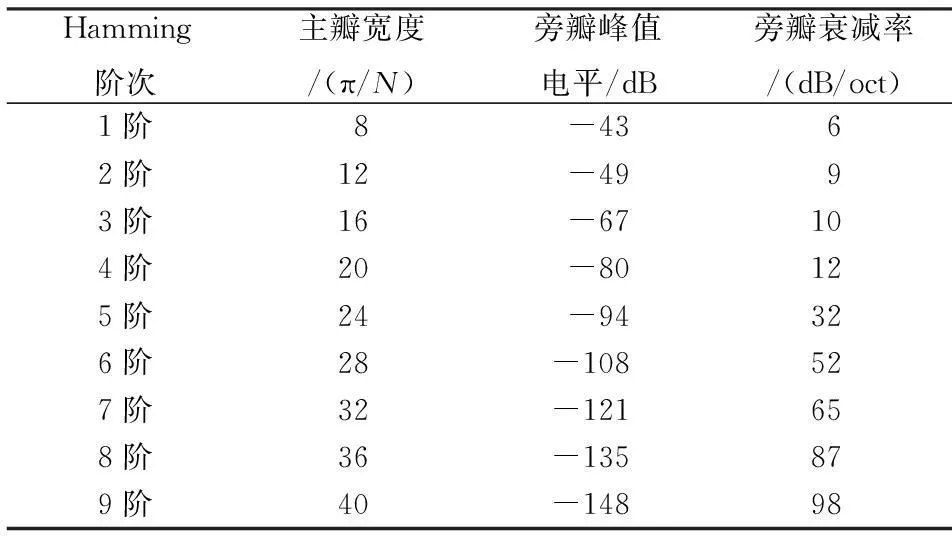
表1　Hamming自乘法窗函數頻譜特性

2四插值算法原理

對單一頻率信號進行分析，假定一個頻率為f0，幅值為A，初始相位為φ的信號x(t)以采樣頻率fs采樣后，得到如下形式的離散信號：

x(n)=Asin(2πnf/fs+φ),

(2)

式中n=0,1,…,N-1，N為采樣點數.

所加離散余弦窗函數的表達式為：

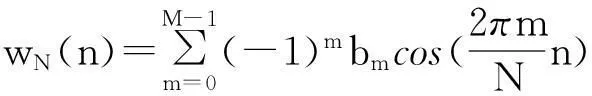
(3)

式中n=0,1,…,N-1;M為窗函數項數；窗函數系數bm滿足如下約束條件：

(4)

對離散信號x(n)進行加窗，得到xw(n)=x(n)w(n)，離散傅里葉變換后得到：

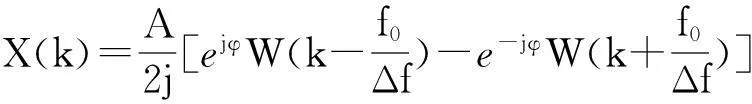
(5)

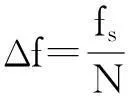
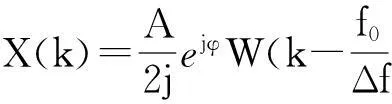
(6)

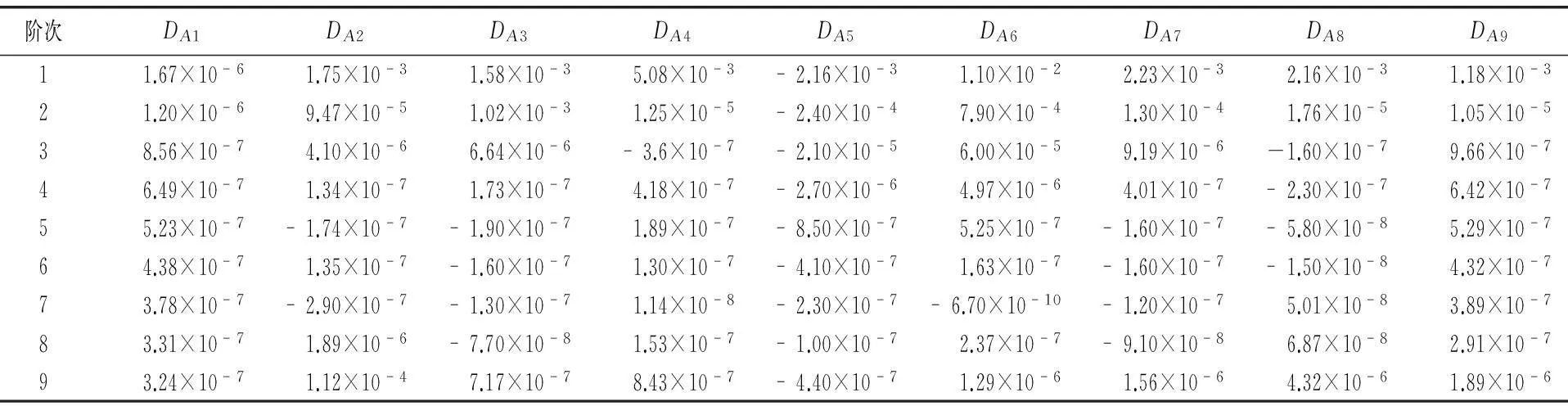
對信號的非同步采樣或非整周期數據截斷時，由于柵欄效應，信號的峰值頻率f0=k0Δf很難剛好位于離散譜線的頻點上，即k0一般不為整數.設峰值頻率點左右各兩條譜線分別為k1

記α=k-k2-0.5，由于0≤k-k2≤1，則-0.5≤α≤0.5，另記：

(7)

根據式(4)和(5)可以得到：

(8)

當N值較大時，式(8)可以化簡為β=g(α)，其反函數為α=g-1(β).由于所采用的余弦窗系數均為實系數，其頻率響應是偶對稱的，因而g(g)和g-1(g)均為奇函數.可采用多項式逼近方法計算奇函數α=g-1(β)，表達式為：

α≈p11β+p13β3+…+p1pβp.

(9)

式中p11,p13,…,p1p為多項式逼近的奇次項系數.

求得α后，得出信號頻率：

f0=kΔf=(k2+α+0.5)Δf.

(10)

信號幅值根據式(6)可知：

(11)

考慮到y2,y3是離真實譜線點最近的兩根譜線，故給予較大權重，可以得到：

(12)

類似式(9)的逼近方法，當N比較大，窗函數系數為實系數，式(12)可表示為：

A=N-1(y4+2.5y3+2.5y2+y1)u(α),

(13)

式中u(g)為偶函數，逼近多項式不含奇次項.四譜線修正逼近多項式如下：

A=N-1(y4+2.5y3+2.5y2+y1)(p20+p22α2+…+

p2dαd),

(14)

其中p20,p22,…，p2d為多項式逼近的偶次項系數.

根據式(6)還可以得出信號的相位：

(15)

根據式(8)、(9)、(11)、(14)、(15)即可進行各次諧波參數的分析.考慮到其中大量窗函數的離散傅里葉分析，其表達式為：

(16)

由于N>>1，可以得到：

(17)

3算法仿真

為了驗證所提算法的精度，進行9次諧波仿真分析.信號模型為：

(18)

式中基波頻率f1為50.5Hz；采樣頻率fs為5120Hz；數據的截斷長度N為1024點.仿真所采用的信號參數如表2所示.

表2　諧波信號參數

對截斷的數據分別加表1所示的自乘法窗函數，然后進行FFT插值分析.以下研究插值算法對檢測精度的影響，修正算法中的擬合多項式次數均取5次，算法流程圖在文獻[7]中有詳細說明，此處不予贅述.

仿真結果由表3～表5給出，其中DAi表示基波和各次諧波幅值測量值的相對誤差，Df0表示基波頻率測量值的相對誤差，Dφi表示基波和各次諧波初始相位測量值的相對誤差，均用百分比表示.

表3　Hamming自乘法窗頻率測量相對誤差

表4　Hamming自乘法窗幅值測量相對誤差

表5　Hamming自乘法窗相位測量相對誤差

由以上的仿真結果可以看出，本文所推導的四譜線插值FFT計算方法，計算結果普遍好于文獻[18]中所述雙譜線和三譜線插值算法；同時從表3～表5數據可以看出，隨著窗函數階次的增加，與文獻[18]的結果比較，四譜線插值在奇數次諧波檢測上的性能提升空間不大，但在偶數次諧波檢測上的精度提升很大，這也是四譜線插值的主要優點.隨著乘法窗函數階次的增加，副瓣衰減變大，可以改善由于非整數截斷帶來的頻譜泄漏；但主瓣越來越寬，對諧波檢測精度是不利的，這點在數據中也有所體現.當乘法窗函數階次提高，窗函數系數會增加，在時域中加窗有時候會相應增加計算量.

4結論

在對信號進行FFT諧波分析時，通過加窗和插值算法可以減少由于非同步采樣或者對數據的非整周期截斷所引起的誤差.本文在各階Hamming自乘法窗函數的基礎上推導了四插值算法.實驗結果表明：本文所提出的四譜線算法總體精度較優，在檢測偶次諧波參數時計算精度更高，具有較高的實用價值.8階自乘法窗函數以下，階次越高計算精度越高，相應時域乘法計算量也會增加，在工程上可根據本文的仿真結果精度選擇合適的窗函數.

參考文獻

[1]Chang G W, Chen C I, Liu Y J, et al. Measuring power system harmonics and interharmonics by an improved fast Fourier transform-based algorithm[J]. IET Gener Transm Distrib, 2008,2(2): 193-201.

[2]Grandke T．Interpolation algorithms for discrete Fourier transform of weighted signals[J]. IEEE Transactions on Instrument and Measurement, 1983, IM-32(2): 350-355.

[3]Ortmeyer T H, Chakravarthi K R, Mahmoud A A. The effects of power system harmonics equipment and loads[J]. IEEE Transactions on Power Apparatus and Systems, 1985, 104(9):2555-2563.

[4]龐浩，李東霞，俎云霄，等. 應用FFT進行電力系統諧波分析的改進算法[J]. 中國電機工程學報，2003, 23(6):50-54.

[5]周俊，王小海，祈才君. 基于Blackman窗函數的插值FFT在電網諧波信號分析中的應用[J]. 浙江大學學報(理學版)，2006, 33(6):650-653.

[6]許珉，張鴻博. 基于Blackman-harris窗的加窗FFT插值修正算法[J]. 鄭州大學學報(工學版)，2005, 26(4):99-101.

[7]卿柏元，滕召勝，高云鵬，等. 基于Nuttall窗雙譜線插值FFT的電力諧波分析方法[J]. 中國電機工程學報，2008, 8(10): 153-158.

[8]曾博，滕召勝，溫和，等. 萊夫-文森特窗插值FFT諧波分析方法[J]. 中國電機工程學報，2009, 29(10): 115-120.

[9]Wen H, Teng Z S, Guo S Y. Triangular self-convolution window with desirable side lobe behaviors for harmonic analysis of power system[J]. IEEE Transactions on Instrumentation & Measurement，2010, 59(3): 543-552.

[10]Zeng B. Parameter estimation of power system signals based on cosine self-convolution window with desirable side-lobe behaviors[J]. IEEE Transactions on power delivery, 2011, 26(1):250-257.

[11]Wen H, Teng Z S, Guo S Y, et al. Hanning self-convolution window and its application to harmonic analysis[J]. Sci China Ser E, 2009, 52(2):467-476.

[12]汪立，劉翠琳. 一種高精度加窗插值FFT諧波分析方法[J]. 陜西電力，2013, 31(5):1-3.

[13]王玲，徐柏榆，盛超，等. 一種新的余弦組合窗插值FFT諧波分析算法[J]. 武漢大學學報(工學版)，2014, 47(2): 250-254.

[14]徐柏榆，王玲，汪立，等．多項Rife-Vincent窗插值諧波分析方法[J]. 武漢大學學報(工學版)，2014, 47(5): 636-641.

[15]Agrez D. Weighted multipoint interpolated DFT to improve amplitude estimation of multi-frequency signal[J]. IEEE Transactions on Instrumentation and Measurement, 2002, 51(2): 287-292.

[16]Wu J, Zhao W. A simple interpolation algorithm for measuring multi-frequency signal based on DFT[J]. Measurement, 2009, 42(2): 322-327.

[17]牛勝鎖，梁志瑞，張建華，等．基于三譜線插值FFT的電力諧波分析算法[J]. 中國電機工程學報，2012，32(16): 130-136.

[18]黃冬梅，龔仁喜，焦鳳昌，等．萊夫-文森特窗三譜線插值的電力諧波分析[J]. 電力系統保護與控制，2014, 42(2): 28-34.

[19]牛勝鎖，梁志瑞，張建華，等．基于四項余弦窗三譜線插值FFT 的諧波檢測方法[J]. 儀器儀表學報，2012, 33(9): 2002-2008.

中圖分類號TM711

文獻標識碼A

文章編號1672-4321(2016)01-0132-04

基金項目國家自然科學基金資助項目(50677048)；中央高校基本科研業務費專項資金資助項目(CZY14008)

作者簡介張俊敏(1977-) ，女，副教授，博士，研究方向：電力系統及其自動化，E-mail: 173902815@qq.com

收稿日期2016-01-04