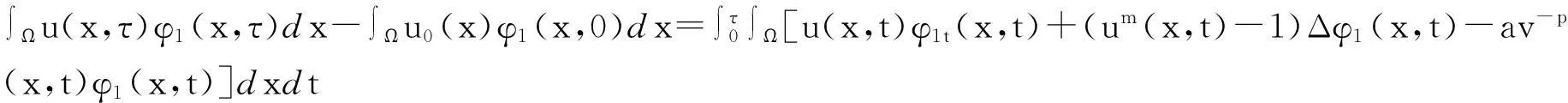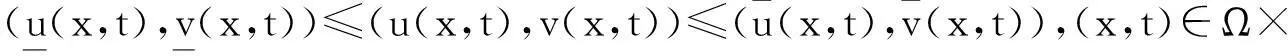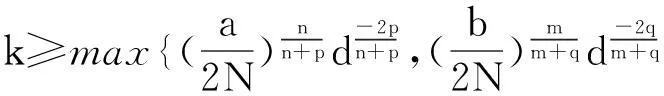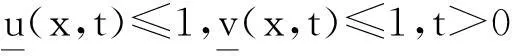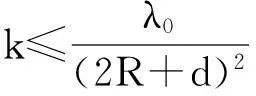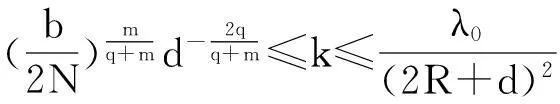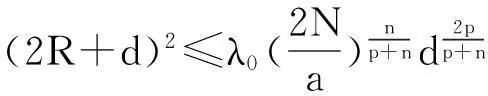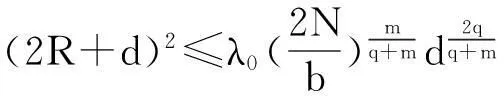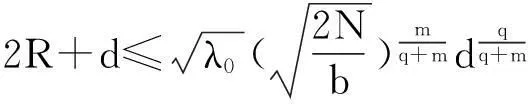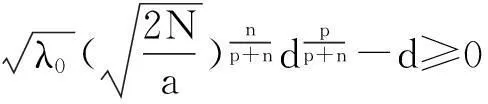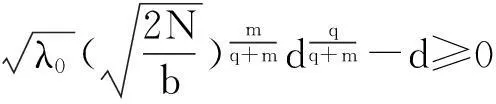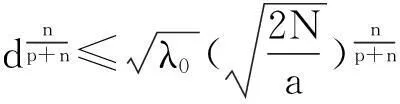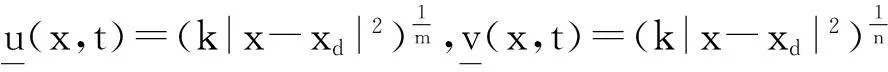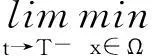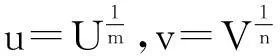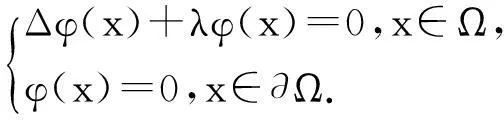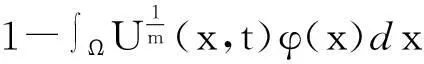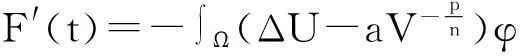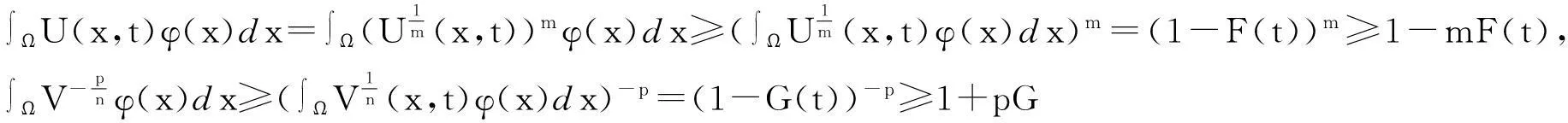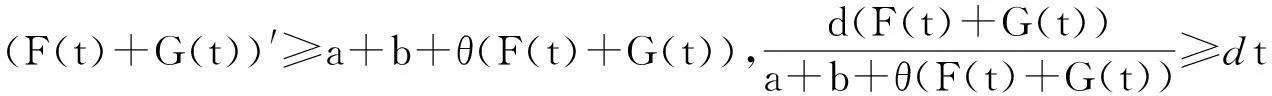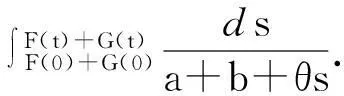一類退縮反應(yīng)擴(kuò)散方程組的整體解的存在性與猝滅

孫仁斌

(中南民族大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)學(xué)院，武漢 430074)

?

一類退縮反應(yīng)擴(kuò)散方程組的整體解的存在性與猝滅

孫仁斌

(中南民族大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)學(xué)院，武漢 430074)

摘要分析了一類退縮反應(yīng)擴(kuò)散方程組的初邊值問(wèn)題，討論了此方程組整體解存在的條件，證明了當(dāng)區(qū)域Ω的直徑適當(dāng)小時(shí)，解是全局存在的；當(dāng)Ω的直徑適當(dāng)大時(shí)，解會(huì)在有限時(shí)刻發(fā)生猝滅現(xiàn)象，得到了Ω直徑的量化范圍．

關(guān)鍵詞退縮反應(yīng)擴(kuò)散方程組；整體解；有限猝滅時(shí)間；區(qū)域直徑

Existence and Quenching of Global Solution for A Class of Degenerate Reaction Diffusion System

SunRenbin

(College of Mathematics and Statistics, South-Central University for Nationalities, Wuhan 430074,China)

AbstractIn this paper, initial-boundary value problem of a class of degenerate reaction diffusion system was analyzed, and existence conditions of global solution of this system were discussed. It was proved that the global solutions exist while the diameter of regionΩis adequate small, yet the solutions would quench in a finite time while the diameter ofΩis adequate large. The range of diameter ofΩwas obtained.

Keywordsdegenerate reaction diffusion system；global solution；finite quenching time；the diameter of region

本文討論如下退縮反應(yīng)擴(kuò)散方程組的初邊值問(wèn)題：

其中Ω是N維空間中具有光滑邊界的有界區(qū)域，常數(shù)a,b,p,q為正實(shí)數(shù),m,n>1,u0(x),v0(x)是連續(xù)函數(shù)，0

問(wèn)題(1)中方程的右邊含有奇異項(xiàng)av-p，bu-q，其解可能會(huì)發(fā)生所謂的猝滅現(xiàn)象．關(guān)于猝滅問(wèn)題的研究，最早由Kawarada在文[1]中提出，此后大量的研究得以展開[2-6]，其中所討論的問(wèn)題大都只涉及到半線性方程或非退化的擬線性方程，其基本結(jié)論是：當(dāng)區(qū)域Ω充分小時(shí)，問(wèn)題的解整體存在；當(dāng)區(qū)域Ω充分大時(shí)，解會(huì)在有限時(shí)刻發(fā)生猝滅．隨著研究的深入，對(duì)于反應(yīng)擴(kuò)散方程組的猝滅現(xiàn)象，近年來(lái)有了一些結(jié)果[7-9]，而對(duì)于退縮方程的研究，也開始有人涉及[10-13]．

本文對(duì)問(wèn)題(1)的討論進(jìn)一步深化，是關(guān)于兩個(gè)函數(shù)耦合的退縮方程組的初邊值問(wèn)題，先通過(guò)上下解方法給出系統(tǒng)的解整體存在時(shí)區(qū)域Ω的直徑應(yīng)滿足的一個(gè)充分條件，再討論解在有限時(shí)刻發(fā)生猝滅時(shí)Ω應(yīng)滿足的充分條件．

1解的存在性

由于問(wèn)題(1)中的方程為退縮的，經(jīng)典的拋物方程理論中關(guān)于解的存在性的討論方法在此并不適用，我們需要討論該問(wèn)題弱解的存在性，為此先給出問(wèn)題(1)弱解的定義．

(2)

則稱u(x,t),v(x,t)為問(wèn)題(1)的弱解．

如果對(duì)任意T>0，方程的弱解都存在，則稱弱解為整體存在．

關(guān)于退縮拋物型方程組弱解的局部存在性，有多種方法可以得到[11,12]，一般都是先構(gòu)造一個(gè)非退縮拋物方程組的初邊值問(wèn)題的序列，再通過(guò)逐步逼近的方法來(lái)得到，限于篇幅，本文在此略去．

下面討論問(wèn)題(1)整體解的存在性，我們采用的上、下解方法在很多討論非退縮方程古典解的存在性時(shí)經(jīng)常用到，而對(duì)于退縮方程組，需要做一些補(bǔ)充，為此，先給出問(wèn)題(1)上、下弱解的定義．

對(duì)于退縮方程組初邊值問(wèn)題的弱解，與古典解一樣，下面的比較原理和存在性定理仍然成立，證明方法可參考文[12]．

根據(jù)定理1，為了得到問(wèn)題(1)解的整體存在性，我們只需找到它的一對(duì)整體存在的上、下解即可．

為了敘述方便，假設(shè)Ω是以原點(diǎn)O為中心，R為半徑的球形區(qū)域：Ω=B(O,R)，當(dāng)Ω是其它形狀的區(qū)域時(shí)，可用同樣方法得到本文的結(jié)論．

(3)

(4)

(5)

為使(3)、(5)式同時(shí)成立，須：

或

(6)

上式右端應(yīng)為正數(shù)，故必須有：

或

即：

(7)

由此可得定理2．

定理2設(shè)常數(shù)d滿足條件(7)，則當(dāng)區(qū)域Ω的半徑R滿足(6)式時(shí)，問(wèn)題(1)的解是整體存在的．

2解的猝滅性

則問(wèn)題(1)轉(zhuǎn)化為如下關(guān)于U(x,t),V(x,t)的初邊值問(wèn)題：

(8)

設(shè)λ1與φ(x)是如下特征值問(wèn)題的第一特征值與相應(yīng)的特征函數(shù)：

(9)

則λ1>0，且x∈Ω時(shí)，φ(x)>0，我們假設(shè)∫Ωφ(x)dx=1，令：

利用問(wèn)題(8)中的方程，我們有：

利用Jensen不等式，有：

F′(t)+G′(t)≥a+b+(bq-mλ1)F(t)+

(ap-nλ1)G(t).

(10)

根據(jù)上面的分析，可以得到定理3．

參考文獻(xiàn)

[1]Kawarada H．On solutions of initial-boundary value problem forut=uxx+1/(1-u)[J]. Publ Res Inst Math Sci, 1975,10：729-736.

[2]Guo J S．On the quenching behavior of the solution of a semilinear parabolic equation[J]. J Math Anal Appl,1990,151：58-79.

[3]Dai Q Y，Gu Y G．A short note on quenching phenomena for semilinear parabolic equations[J]. J Differential Equations, 1997,137：240-250.

[4]Salin T．On quenching with logarithmic singularity[J]. Nonlinear Analysis,2003,52：261-289．

[5]Bertdch M, Ughi M．Positivity peoperties of viscosity solutions of a degenerate parabolic equation[J].Nonlinear Analysis,1990,14：571-592．

[6]孫仁斌．含有對(duì)數(shù)奇異項(xiàng)的拋物方程解的整體存在性與猝滅性[J]．江西師范大學(xué)學(xué)報(bào)(自然科學(xué)版)，2006,30(4)：307-310．

[7]Pablo A, Quiros F, Rossi J D．Non-simultaneous quenching[J]. Appl Math Lett, 2002,15：265-269．

[8]Ferreira R，Pablo A，Quiros F．Non-simultaneous quenching in a system of heat equations coupled at the boundary[J]．Z Angew Math Phys, 2006,57：586-594．

[9]Zheng Sining, Wang Wei．Non-simultaneous versus simultaneous quenching in a coupled nonlinear parabolic system[J]．Nonlinear Analysis, 2008,69：2274-2285．

[10]Winkler M．Quenching phenomena in strongly degenerate diffusion equations with strong absorption[J]. J Math Anal Appl，2003,288：481-504．

[11]Winkler M．Infinite-time quenching in a fast diffusion equation with strong absorption[J]. Nonl Diff Equ Appl, 2009,16：41-61．

[12]Yang Ying，Yin Jingxue，Jin Chunhua．A quenching phenomenon for one-dimensionalp-laplacian with singular boundary flux[J]．Appl Math Lett, 2010,23：955-959．

[13]孫仁斌．含有奇異項(xiàng)的退縮拋物方程解的整體存在性與有限時(shí)刻猝滅性[J]．中南民族大學(xué)學(xué)報(bào)(自然科學(xué)版)，2013，32(1)：102-105．

[14]Anderson J R．Local existence and uniqueness of solutions of degenerate parabolic equations [J].Comm Partial Differential Equations,1991,16：105-143．

[15]Aronson D G, Crandall M, Peletier L A．Stabilization of solutions of a degenerate nonlinear diffusion problem[J].Nonlinear Analysis,1982,6：1001-1022．

[16]Anderson J R, Deng K．Global existence for degenerate parabolic equations with a non-local forcing[J].Methods Appl Sci,1997,20：1069-1087．

中圖分類號(hào)O175.26

文獻(xiàn)標(biāo)識(shí)碼A

文章編號(hào)1672-4321(2016)01-0141-04

基金項(xiàng)目國(guó)家自然科學(xué)基金資助項(xiàng)目(61374085) 國(guó)家自然科學(xué)基金資助項(xiàng)目(11301552)；中南民族大學(xué)研究生創(chuàng)新基金資助項(xiàng)目(2016sycxjj135)

作者簡(jiǎn)介孫仁斌(1964-)，男， 副教授，研究方向：拋物型偏微分方程，E-mail：sunrenbin@foxmail.com 夏永波(1979-)，男，副教授，博士，研究方向：編碼與密碼學(xué)，E-mail:xia@mail.scuec.edu.cn

收稿日期2016-02-21 2015-12-03