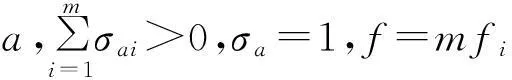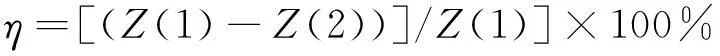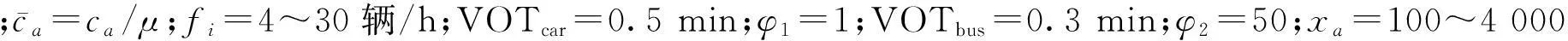基于雙層規劃的城市公交專用道優化設計

陳　芳,　龍建成

(合肥工業大學 交通運輸工程學院,安徽 合肥　230009)

?

基于雙層規劃的城市公交專用道優化設計

陳芳,龍建成

(合肥工業大學 交通運輸工程學院,安徽 合肥230009)

摘要:為了提高公交車的服務水平,很多城市開辟了公交專用道,由于公交專用道的設置會降低小汽車的路權,必須從系統整體的角度來設置公交專用道以科學權衡小汽車與公交車的路權分配。文章從城市交通網絡的整體出發,以出行者總體出行成本最小為目標,充分考慮出行者的出行選擇行為,提出了城市公交專用道優化設計的雙層規劃模型;結合設置公交專用道的路段上公交車與小汽車的流量特性,提出了基于公交專用道網絡的道路阻抗函數,構造雙模式交通分配模型;分別使用Frank-Wolfe算法和遺傳算法進行下層流量分配和雙層規劃模型的求解,并運用交通網絡進行實例分析,驗證了所提模型和算法的有效性。

關鍵詞:公交專用道;雙層規劃;用戶平衡;交通配流;遺傳算法

為了緩解交通擁堵的壓力,大力發展公共交通已經成為各大城市發展的趨勢,最為傳統的公共交通方式便是常規公交,但是由于中間停靠站的設置會引起行駛時間的延誤,而且公交車與社會車輛之間也存在嚴重的路權沖突,致使公交車平均行駛速度較低。為了解決這一問題,提高公共交通的吸引力,越來越多的城市開始設置公交專用道,但是大多是零散設置,缺少系統規劃。因此,有必要將以前單條布設的公交專用道進行重新規劃,使其網絡化、系統化[1],同時綜合考慮社會車輛和公交車之間的路權分配問題,從道路系統的整體出發,合理權衡兩者所承載的利益群體之間的關系,實現交通網絡總體通行效率的提高。這是本文研究的重點內容。

對于公交專用道網絡的設計問題,可以將各個路段是否設置專用道作為一個0-1變量來考慮,交通管理部門確定專用道網絡設置方案后,出行者則依據此方案自主選擇交通方式與出行路徑,并最終達到用戶均衡狀態。這是典型的離散網絡設計問題[2-3],可以用雙層規劃模型來描述。

1公交專用道設置問題概述

1.1下層出行者交通選擇問題

1.1.1基本假設

本文研究做出如下基本假設:

(1) 只考慮小汽車和公交車2種出行方式,且自由流狀態下的路段通行時間相同。

(2) 公交專用道分為路側型和路中型[4],忽略其對路段通行能力的影響。

(3) 只考慮將路段上已有的1條車道調整為公交專用道,不考慮路段增加1條車道作為公交專用道。

(4) 在設置公交專用道的路段上,公交車均在公交專用道上行駛,且任一條公交線路的往返路程所經路段相同且固定。

(5) 每條公交線路的發車頻率相同,且忽略公交車在停靠站及交叉口處的延誤。

(6) 下層模型為確定性用戶均衡分配[5],即假設司機都力圖選擇阻抗最小的路徑且能夠準確地計算每條路徑的阻抗。每個OD(Origin-to-Destination)對之間的交通需求是固定且已知的。

(7) 小汽車駕駛員按照Wardrop第一原理[6]選擇路徑,公交車乘客不進行路徑選擇,而是根據公交車的發車頻率和標準單車乘車人數計算單位時間內的運送能力,將這部分運送總量從網絡總出行量中減去,再對剩余的小汽車出行量進行交通均衡分配。

1.1.2出行方式選擇

通常情況下,出行者在進行出行方式的選擇時會優先考慮一些類似時間、價格、換乘次數等可預知的確定性因素,也會因其他條件而考慮一些不確定性因素,如天氣、交通事故及一些臨時交通管制措施等。為簡便起見,本文對公交專用道的設置規劃只考慮出行時間和價值。

1.1.3出行路徑選擇

在城市交通網絡中,出行者在選擇出行方式之后,需要選擇出行路徑。在路徑選擇過程中考慮的主要因素是路徑時間和費用,即起訖點間用時最短和花費最少的路徑。

根據用戶平衡條件,本文中小汽車出行者的路徑選擇原則符合Wardrop第一原理,即在城市混合交通網絡中,對于一種交通方式來說,起訖點之間所有可供選擇的路徑中,出行者所選擇的各條路徑上該交通方式的出行費用相等,并且不大于未被使用的路徑上該交通方式的出行費用。

1.2上層優化目標

本文規劃的目標是使整個道路網絡系統的總體出行成本最低,而不是單純地提高公交車出行比例。因此,基于公交專用道的城市交通網絡優化目標是考慮在設置公交專用道的條件下,依據出行者的交通選擇行為,優化專用道網絡的設置,使得交通網絡中出行者的總體出行成本達到最低,即系統最優,從而使得在有限的交通資源條件下,城市道路網絡可以滿足更多的出行需求。

2公交專用道雙層規劃模型

考慮節點集合N和路段集合A0構成的城市道路交通網絡G0(N,A0)。假設有n1個路段可以建設公交專用道,集合為A1,記路段為a,a∈A1,A1∈A0。對于n1個備選路段,則有2n1個建設方案。規劃目標是從2n1個建設方案中選擇最優的方案,使得整個網絡出行者出行成本最低。

2.1符號及變量定義

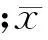
2.2路段阻抗函數

本文中,公交專用道網絡的路段分為3種:① 沒有公交線路通過的路段,稱為“小汽車路段”;② 設置有公交專用道的“雙模式”路段;③ 公交車與小汽車共享的“雙模式”路段。

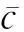
(1) 設置有公交專用道“雙模式”路段上小汽車的單人出行成本函數為:

(1)

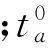
(2) “小汽車路段”上小汽車單人出行成本函數為:

(2)

(3) 小汽車與公交車共享的“雙模式”路段上小汽車單人出行成本函數為:

(3)

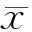
(4) 公交車在公交專用道上行駛時,公交車乘客單人出行成本函數為:

(4)

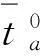
(5) 小汽車與公交車共享路段上公交車乘客單人出行成本函數為:

(5)

對上述公式引入決策變量,總結如下。

(1) 小汽車在路段a上單人出行成本函數為:

(6)

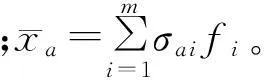
(2) 公交車在路段a上單人出行成本函數為:

(7)

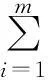
2.3下層出行者路徑選擇模型

下層出行者根據決策者設計的方案進行出行選擇,可以用均衡配流模型來描述。

(8)

(9)

(10)

(11)

下層模型目標函數為所有路段小汽車阻抗函數的積分和。(9)式表示路徑上小汽車的流量與OD流量之間的守恒關系,(10)式保證所有路徑之間的小汽車流量非負,而(11)式描述了路段流量和路徑流量的關系。

2.4上層優化模型

上層決策者通過制定公交專用道網絡設計方案,使系統的總體出行成本最小的最優模型表達式為：

(12)

(13)

(12)式中,括號中第1項為選擇小汽車的出行者總體出行成本,第2項為公交車乘客的總體出行成本;(13)式表示上層決策變量λa為0-1變量。

3公交專用道雙層規劃模型的求解

3.1下層出行者路徑選擇模型的求解

Frank-Wolfe算法[12]是利用線性規劃逐步逼近非線性規劃的方法來求解UE模型,該方法在每步迭代中找到一個最速下降方向和最優步長,在最速下降方向上截取最優步長得到下一步迭代起點,重復迭代直至找到最優解。方法步驟如下:

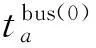
(4) 尋找迭代步長。求解滿足(14)式的an。

0≤an≤1

(14)

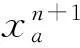
3.2公交專用道雙層規劃模型的求解

本文選用遺傳算法[13]求解雙層規劃模型,求解過程如下:

(1) 初始化參數設置。主要包括種群大小PS、最大遺傳代數MS、變異概率pm、交叉概率pc、收斂精度ρ、終止檢驗代數s,運用錦標賽方法產生初始群體G(0),并置t=0。

(2) 用方向搜索法對G(t)中的個體進行交通分配。

(4) 交叉操作。依據交叉概率pc,從G(t)中選擇個體配對進行交叉,把交叉得到的子輩添加到子輩集合G′(t)中。

(5) 變異操作。依據變異概率pm對G(t)中的個體基因位進行變異,得到的子輩添加到子輩G′(t)中。

(6) 產生下一代。利用復制算法得到下一代群體G(t+1)。

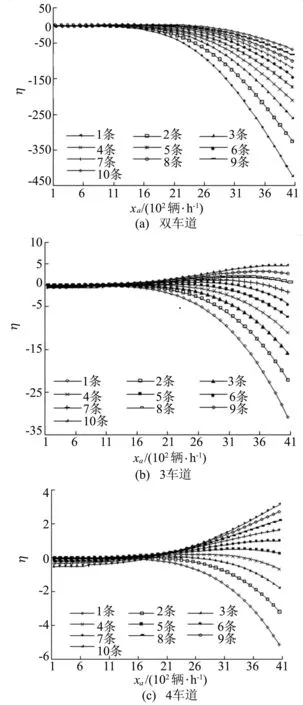
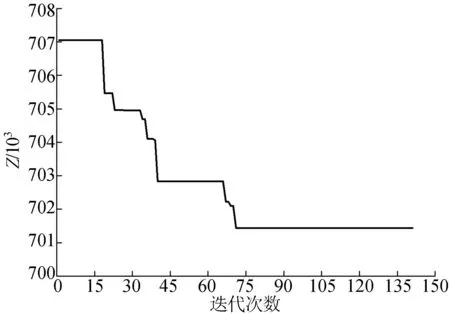
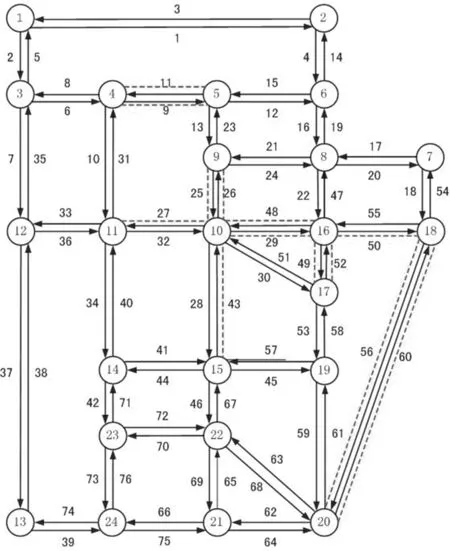
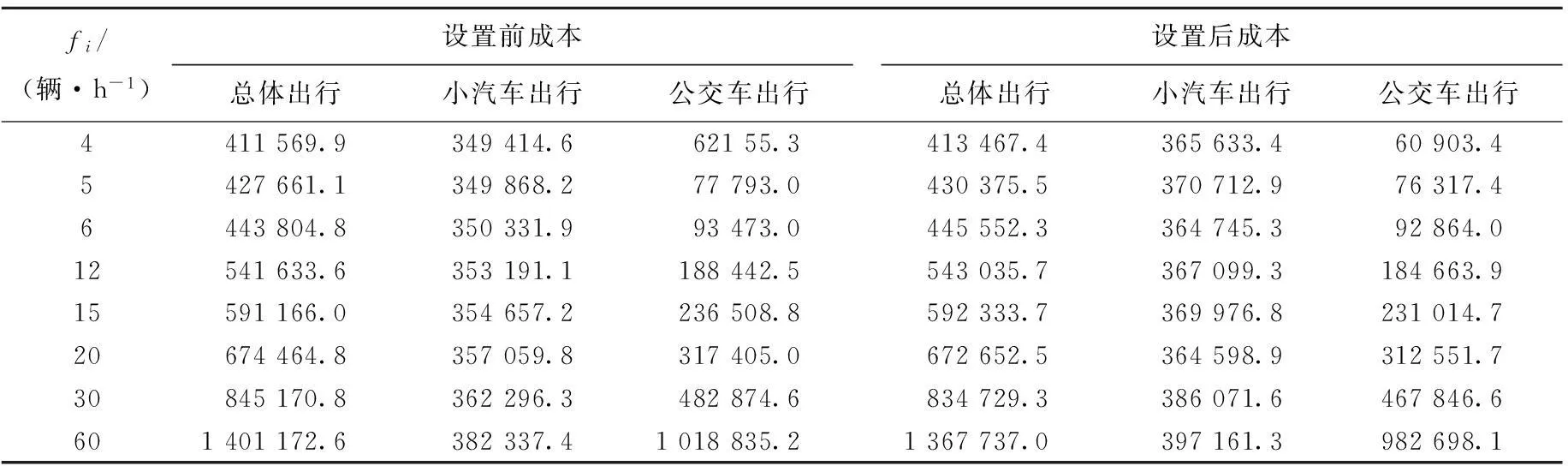
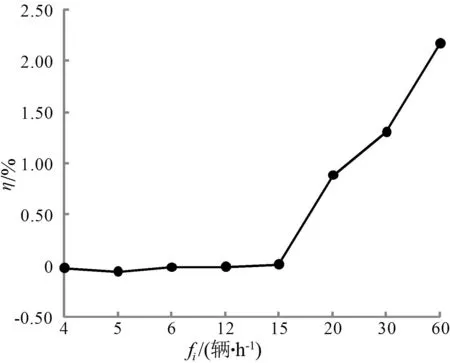
(7) 如果t

(8) 算法結束。輸出最優個體對應的方案{gu}。

4算例分析

4.1單路段公交專用道設置分析

進行單路段分析需要計算路段a在設置公交專用道前后的出行者出行成本，為了更清楚地觀察公交專用道設置前后出行成本的變化情況,設置參數η,其含義為設置公交專用道的效率,通過對η值判斷,便可確定在路段a上設置公交專用道是否有效。η的計算公式為:

(15)

其中,Z(1)為路段a上不設置公交專用道,即λa=0時的出行成本;Z(2)是路段a上設置公交專用道,即λa=1時的出行成本。

當η>0時,表明設置公交專用道對于降低出行者出行成本有效果,并需要對η值做仔細分析;如果η≤0,則表明設置公交專用道沒有作用。

通過單一變量控制,得到在不同車道數的路段上η與路段a上小汽車流量xa、通過該路段的公交線路條數m的關系圖,如圖1所示。

由圖1可以看出,在雙車道的路段上設置公交專用道對降低出行者出行成本沒有效果,反而使得出行者總體出行成本增加,因此,在公交線網規劃時,不應該在雙車道的路段上設置過多公交線路,更不適宜設置公交專用道;對于3車道的路段,當公交線路條數m≥4條、小汽車流量xa≥1 600輛/h時可以考慮設置公交專用道;同理,4車道的路段上,當公交線路條數m≥4條、小汽車流量xa≥1 600輛/h時,設置公交專用道對于降低總體出行成本更為有利。

圖1　不同車道數的路段η與xa的關系

4.2SiouxFalls網絡上公交專用道設置分析

本文采用的Sioux Falls網絡[14],包含24個節點、76條路段以及528個OD對,各路段的屬性如圖2所示,各條路段的車道數及路段實際通行能力見表1所列。為了符合我國城市公交系統的特點,對該網絡的公交線網進行優化調整,如圖3所示,每條公交線路Li通過的節點見表2所列。

(1) 最優公交專用道設置方案。部分參數設置如下:種群大小PS=20,最大遺傳代數MS=140,變異概率pm=0.08,交叉概率pc=0.4,其余路段參數設置同4.1節。

由于遺傳算法運算過程中存在隨機性,因此每次運行的結果存在一些差異。從中選出20次運行結果,見表3所列。從表3中可以看出,在各個參數值已定的情況下,最優公交專用道設置方案中,公交專用道設置效率η的平均值約為1.06%,對于整個網絡而言,此效果是明顯的。

圖2　Sioux Falls網絡圖

路段naca/(輛·h-1)路段naca/(輛·h-1)1和31161933和36212272和51146334和40312194和141124037和38216196和82142639和74212737和351146341和44212829和114148242和711123110和311122745和574121412和152123746和674120013和232125049和524130716和193122550和553164017和201196053和583120618和543146356和604146321和241126359和611125122和473126162和641126525和264173963和681126927和324125065和692130728和434168966和753122129和484121470和721125030和511124873和7611270

圖3　Sioux Falls公交網絡圖

Li所經節點Li所經節點15,4,11,14157,18,16,10,15,22,21,2421,3,4,5,9,10,16,17,19167,18,16,10,1132,6,5,4,11,10,15,22173,12,11,10,16,18,2044,5,6,8,7187,18,16,17,19,15,22,2354,5,9,10,15,22196,8,16,17,19,15,22,23618,20,21,24209,10,11,12,1374,5,9,10,15,22,21,24,132118,20,2289,10,16,18,20229,10,16,18,2091,2,6,8,16,17,192311,14,15,19108,9,10,112411,10,16,18,201114,15,19,17,16,8255,4,3,12,13126,8,16,10,15,222612,13,24,21136,8,16,17,19,15,14,232712,11,10,15,19146,8,16,18,20

表3　遺傳算法求解結果

為了觀察遺傳算法在一次計算中求得的結果是最優的,取其中最好的一次結果,即第13次,繪制求解過程,如圖4所示。從圖4中可以看出,在經過140次的迭代之后,網絡總體出行成本達到最低。

圖4　遺傳算法求解過程圖

從表3中選取出行者出行成本最低的公交專用道方案作為最優方案,即第13次運行結果,規劃方案繪制如圖5中的虛線部分。

圖5　公交專用道網絡優化圖

(2) 靈敏度分析。對于公交網絡,公交線路固定后,線路發車頻率fi直接決定了公交車的流量,進而影響總體出行成本的大小。

出行者出行成本隨著公交車發車頻率改變而變化的情況見表4所列。

表4　不同頻率下遺傳算法求解結果　元

在設置專用道后,公交車發車頻率的變化對降低出行者出行成本的影響如圖6所示。

由圖6可以看出,公交車發車頻率越高,η的值越大,設置專用道的效果越好;而公交車發車頻率較低時,設置公交專用道反而會增加出行者的總體出行成本。

不同小汽車交通需求水平下公交專用道的設置效率η見表5所列。由表5可知,小汽車的交通需求水平對于整個交通網絡的出行成本影響很大,且影響效果波動較大。

圖6　公交專用道設置效率與公交車發車頻率的關系

元

5結束語

本文在現有的離散交通網絡設計問題研究的基礎上,從交通系統的總體角度出發,以出行者總體出行成本最小為目標,采用雙層規劃模型來描述公交專用道網絡的優化設置,并且分析了在不同的道路車道數目、小汽車需求水平和公交車的

發車頻率下公交專用道的設置效果。本文研究結果為公交專用道的設計提供了可量化的依據。

[參考文獻]

[1]莫一魁,柳伍生,晏克非.大城市公交專用道網絡設計優化技術研究[J].交通科技與經濟,2007,2(9):102-104.

[2]高自友,張好智,孫會君. 城市交通網絡設計問題中雙層規劃模型、方法及應用[J].交通運輸系統工程與信息,2004,4 (1):35-37.

[3]Miandoabchi E, Daneshzand F, Szeto W Y, et al. Multiobjective discrete urban road network design [J]. Computers and Operations Research, 2013, 40(10):2429-2449.

[4]李彬，郭冠英，楊東援.城市公共交通專用道規劃研究[J].合肥工業大學學報：自然科學版，1999，22(3)：57-61.

[5]黃海軍. 城市交通網絡平衡分析：理論與實踐[M].北京:人民交通出版社,1994:12-13.

[6]Wardrop J G. Some theoretical aspects of road traffic research [J].Proceedings of the Institutionof Civil Engineers,1952,1(3): 325-362.

[7]何南,趙勝川. 城市道路阻抗函數研究:以大連市為例[J].公路交通科技,2014,31(2):104-108.

[8]劉春年,鄧青菁. 應急決策信息系統最優路徑研究:基于路阻函數理論及Dijkstra算法[J].災害學,2014,29(3):18-22.

[9]Szeto W Y, Lo H K. Strategies for road network design over time: robustness under uncertainty [J]. Transportmetrica, 2005,1(1): 47-63.

[10]Szeto W Y, Lo H K. Transportation network improvement and tolling strategies: the issue of intergeneration equity [J].Transportation Research A, 2006, 40(3):227-243.

[11]Szeto W Y, Lo H K.Time-dependent transport network improvement and tolling strategies [J]. Transportation Research A, 2008, 42(2):376-391.

[12]Long J C, Gao Z Y, Zhang H Z, et al. A turning restriction design problem in urban road networks [J]. European Journal of Operational Research,2010,206(3):569-578.

[13]周明,孫樹棟.遺傳算法原理及應用[M]. 北京:國防工業出版社,1999:6-64.

[14]LeBlanc L J.An algorithm for the discrete network design problem [J].Transportation Science, 1975, 9(3):183-199.

(責任編輯胡亞敏)

Optimum design of city bus lane based on bi-level programming

CHEN Fang,LONG Jian-cheng

(School of Transportation Engineering, Hefei University of Technology, Hefei 230009, China)

Abstract:In order to improve the bus service level, more and more cities have opened the bus lanes. But the bus lanes will aggravate the car right, thus the relationship between the car and the bus should be balanced scientifically from the perspective of overall system. In order to guarantee the minimum travel cost of the traveler, and considering the travel selection behavior of the traveler, a bi-level programming model for bus lane network optimization is built from the perspective of the whole city traffic network. According to the flow characteristic of the car and the bus on the road with bus lanes, the impedance function based on bus lane network is proposed and the dual-mode traffic assignment model is established. The lower-layer flow assignment and the bi-level programming model are solved by using the Frank-Wolfe algorithm and the genetic algorithm respectively. Finally, the example analysis with real traffic network is carried out to verify the validity of the proposed model and algorithm.

Key words:bus lane; bi-level programming; user equilibrium; traffic flow assignment; genetic algorithm

中圖分類號:U491.1

文獻標識碼：A

文章編號：1003-5060(2016)03-0296-08

doi:10.3969/j.issn.1003-5060.2016.03.002

作者簡介：陳芳(1991-),女,安徽宿州人,合肥工業大學碩士生;龍建成(1983-),男,湖南祁東人,博士,合肥工業大學教授,博士生導師.

基金項目：國家自然科學基金重點資助項目(71431003)

收稿日期：2015-01-22；修回日期：2015-03-20