Timoshenko梁模型下完整樁瞬態橫向振動半解析解

龍麗麗,　劉東甲,　蔣　紅

(1.安徽水利水電職業技術學院 市政工程系,安徽 合肥　231603; 2.合肥工業大學 資源與環境工程學院,安徽 合肥　230009)

?

Timoshenko梁模型下完整樁瞬態橫向振動半解析解

龍麗麗1,劉東甲2,蔣紅1

(1.安徽水利水電職業技術學院 市政工程系,安徽 合肥231603; 2.合肥工業大學 資源與環境工程學院,安徽 合肥230009)

摘要:文章采用Timoshenko梁模型下樁-土系統橫向振動的動力學模型和數學模型,通過Laplace變換,得到樁頂橫向振動速度在頻域內的解析解,進行快速Fourier逆變換,得到樁頂速度時域內的表達式;根據試驗樁參數繪制出速度導納曲線及樁頂速度曲線,分析Bernoulli-Euler梁模型和Timoshenko梁模型的速度導納曲線的特點,對比2種模型樁的理論速度曲線與試驗樁實測速度曲線的差異;分析不同參數對樁頂橫向動力響應的影響。結果表明,Timoshenko梁模型的結果比Bernoulli-Euler梁模型更接近于工程實際中低應變橫向測樁的結果,所得半解析解結果能在頻域內進行分析,具有很好的適應性和準確性。

關鍵詞:Timoshenko梁;瞬態橫向動力響應;傳遞函數;導納曲線

對于瞬態沖擊下單樁的橫向動力響應,建立的動力學模型和數學模型主要分為3種：Bernoulli-Euler梁模型、Timoshenko梁模型及Reddy三階梁模型。其中Bernoulli-Euler梁模型不考慮樁的剪切作用和轉動慣量的作用[1-4],在分析單樁的水平振動問題時會帶來較大誤差[5],且在低應變測樁橫向動力響應分析時會出現頻散的現象,導致無法判別樁底反射[3]。Reddy三階梁模型考慮了梁在沖擊作用下的剪切作用,但是高階梁模型建立非常復雜,計算工作量非常大,更多用于復合材料層合板的分析[6-7]。而Timoshenko梁模型作為一階梁,模型建立相對簡單,同時又考慮了剪切作用的影響[8],應用于沖擊荷載作用下樁身動力響應問題中效果較好[9],低應變測樁研究中,該模型下得到的速度曲線與工程實測曲線非常接近,是研究低應變測樁橫向動力響應的很好的模型[10]。以往在Timoshenko梁模型下樁-土系統橫向動力響應的研究主要集中在頻率域內剛度、彎矩、剪力等內容的研究,然而,系統振動的速度更本質地描述了系統的運動過程,速度導納作為理論傳遞函數時,對于離散系統是嚴格精確的,對于連續系統,可期望獲得滿足工程精度的結果[11]。而且,工程人員更習慣對于時域內的動力參數進行分析和處理。

本文采用Timoshenko梁模型下完整樁的橫向振動動力學模型,考慮樁底鉸接、樁底自由和樁底固定3種情況,通過方程組的處理,進行Laplace變換,解析地得到了頻域內樁-土系統關于樁頂橫向振動速度的傳遞函數和樁頂速度的頻率響應函數,繪制出速度導納曲線,然后通過快速Fourier逆變換繪制出時域內的樁頂速度曲線。將Timoshenko梁模型下的速度導納曲線和樁頂速度曲線與Bernoulli-Euler梁和實測完整樁速度曲線對比,并分析不同參數對樁頂橫向動力響應的影響,得到的結論為樁的瞬態橫向振動理論分析提供了基礎,也為工程人員橫向測樁提供了依據。

1完整樁橫向振動定解問題

根據Timoshenko梁振動理論[12-13],文獻[10]推導出橫向振動微分方程為:

(1)

(2)

其中,u(z,t)為橫向位移;θ(z,t)為截面彎曲所產生的轉角;E為樁的彈性模量;G為樁的剪切彈性模量;J為樁截面對中性軸的慣性矩;A為橫截面面積;ρ為樁身密度;k′為取決于橫截面形狀的數值因子;k為樁周土剛度系數;c為阻尼系數;k、c的簡化式參考文獻[14]的(4)式。

初始條件為:

樁頂邊界條件為:

(3)

(4)

其中,q為剪力;m為彎矩;p(t)為樁頂橫向激振力[15]。

樁底邊界條件考慮為鉸接:

2定解問題的求解

將(1)式、(2)式分別消去θ和u,可得:

(5)

(6)

考慮初始條件,對(5)式、(6)式作Laplace變換,可得:

(7)

(8)

其中,U(z,s)為u(z,t)的Laplace變換;Θ(z,s)為θ(z,t)的Laplace變換。

(9)

(10)

方程(7)式、(8)式的通解為:

U(z,s)=C1cosαz+C2sinαz+

C3cosβz+C4sinβz

(11)

Θ(z,s)=D1sinαz+D2cosαz+

D3sinβz+D4cosβz

(12)

對(2)式作Laplace變換,可得:

(13)

將(11)式、(12)式代入(13)式,有

(ρJs2+k′AG)(D1sinαz+D2cosαz+

D3sinβz+D4cosβz)-k′AG(-αC1sinαz+

EJ(-α2D1sinαz-α2D2cosαz-

β2D3sinβz-β2D4cosβz)=0

(14)

為了滿足(14)式成立,系數C1～C4、D1～D4滿足以下關系:

(15)

其中

令z=0,對(3)式、(4)式分別進行Laplace變換,并將(11)式、(12)式、(15)式代入計算得:

(16)

(17)

考慮樁底邊界條件為鉸接情形,令z=l,有

(18)

βηC3cosβl-βηC4sinβl=0

(19)

聯立(16)～(19)式,解得:

(20)

其中

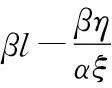
P(s)為p(t)的Laplace變換。

3樁頂橫向動力響應

在低應變動力測樁中,測定的一般為樁頂橫向振動速度v(t)。v(t)的Laplace變換為:

在(11)式中,令z=0,則U(z,s)|z=0=C1+C3,將(20)式代入,得樁-土系統關于樁頂橫向振動速度的傳遞函數為:

(21)

在(21)式中令s=iω,得樁頂速度的頻率響應函數為:

(22)

樁頂速度頻譜為:

(23)

最后,由(23)式的Fourier逆變換得到時域的樁頂速度v(t):

(24)

4工程實測算例

為了檢驗以上樁土模型及頻域解析解對于低應變測樁橫向振動問題的實用性,測試了合肥工業大學緯地樓前1#試驗樁,得到樁頂橫向振動的實測速度曲線。試驗樁樁長l=7 m,樁徑d=0.8 m,樁徑比l/d=8.75。

參考試驗樁樁身及樁周土條件,按以上推導過程進行理論速度曲線模擬計算,參數設置如下:樁的質量密度ρ=2 400 kg/m3,泊松比υ=0.28,彈性模量E=33.75 GPa;樁周土剪切波速vs=100 m/s,密度ρs=1 700 kg/m3,泊松比υs=0.4;橫截面形狀的數值因子k′=3/4;樁頂橫向激振力沖量和作用時間分別為I=1 N·s,t0=1.0 ms。

將本文Timoshenko梁模型下半解析解結果繪制成理論速度曲線,與試驗樁實測速度曲線和Bernoulli-Euler梁模型下理論速度曲線一起進行歸一化處理,速度曲線對比如圖1所示。可以看出,Bernoulli-Euler梁速度曲線與實測速度曲線的入射反射同步進行,但是由于頻散,Bernoulli-Euler梁在樁底反射前即已產生了波動,與實測曲線的樁底反射時間相差甚遠;而Timoshenko梁理論速度曲線,入射與樁底反射都能很好地與實測速度曲線進行擬合,在0.6 ms處入射波同時達到峰值,6.4 ms處開始出現樁底反射,樁底反射在同相位、反相位之間反復變化,且2條曲線的相位變化趨勢一致。

Timoshenko梁模型與Bernoulli-Euler梁模型的速度導納對比如圖2所示。

圖1　速度曲線對比

圖2　速度導納曲線對比

圖2中Bernoulli-Euler梁模型的速度導納曲線出現相鄰峰頻差Δf隨頻率增大而增大的現象;而Timoshenko梁模型速度導納曲線的Δf基本相等,這是樁底反射波(見圖1)的反映,從另一方面印證了Timoshenko梁考慮到了樁的剪切作用,在橫向振動問題的研究中,頻散相對較小。

不同樁底約束情況下速度曲線對比如圖3所示。

本文建立的定解問題中,樁底邊界條件考慮為彈性約束鉸接。為了分析不同樁底邊界條件的特點,圖3考慮了樁底固定、自由和絞接3種情況。圖3a樁徑比l/d=8.75,可以看出,樁底自由時最先發生樁底反射,樁底固定和樁底鉸接的情況幾乎同時發生樁底反射,但是樁底鉸接的反射波峰值比樁底固定的情況更大。圖3b中,樁徑取d=0.4 m,樁徑比l/d=17.5,圖中3種樁底邊界條件的樁底反射時間及反射峰值均非常接近。文獻[4]指出,在一般的樁土剛度比情況下,當l/d=10時,樁底條件對整個反應曲線影響較大,而當l/d=15時,樁底固定、自由和鉸接3種邊界條件的結果非常接近。

圖3　不同樁底約束結果對比

本文半解析解結果與文獻[10]差分法結果理論速度曲線的對比如圖4所示。

圖4　不同算法結果對比

可以看出2種方法的結果比較接近,差分法的入射反射和樁底反射相對偏早,且入射波的峰值與本文的結果相比較小。由本文的半解析解結果可以繪制出速度導納曲線,從理論分析的角度來說,可以在頻域內對動剛度等內容進行分析;同時從工程實踐的角度,還可以從頻域內獲得更多的樁身完整性信息[16]。

5橫向振動響應參數分析

不同樁長時的橫向動力響應如圖5所示。

從圖5a可以看出,樁底發生反射時間的早晚與樁長成正比。但是,與縱向振動不同,橫向振動樁底反射的相位不是確定的,而是在同相位、反相位之間反復變化。這點在圖1的實測曲線中也得到了驗證。圖5b中,速度導納曲線的相鄰峰頻差Δf反應了樁的長度,樁長越長,相鄰峰頻差越小;相鄰峰谷幅度差ΔN反應了樁-土系統的阻尼特性,樁長越長,阻尼越大。

圖5　不同樁長橫向動力響應

不同樁徑下的橫向動力響應如圖6所示。

圖6a中,隨著樁徑的增加,入射波的峰值減小。由于樁徑越大樁頂橫向動剛度越大,入射波峰值過后樁徑d=1.2 m的速度曲線在最上方,最接近圖中所示零刻度線,處于中間的是樁徑d=0.8 m的速度曲線,樁徑d=0.4 m的速度曲線位于最下方。

圖6b同樣也反映了樁頂的橫向動剛度,樁徑d=0.4 m的樁頂橫向動剛度最小,所以導納曲線初始部分的斜率最大,樁徑d=0.8 m的斜率居中,樁徑d=1.2 m的斜率最小。

圖6　不同樁徑橫向動力響應

不同剪切波速的橫向動力響應如圖7所示。

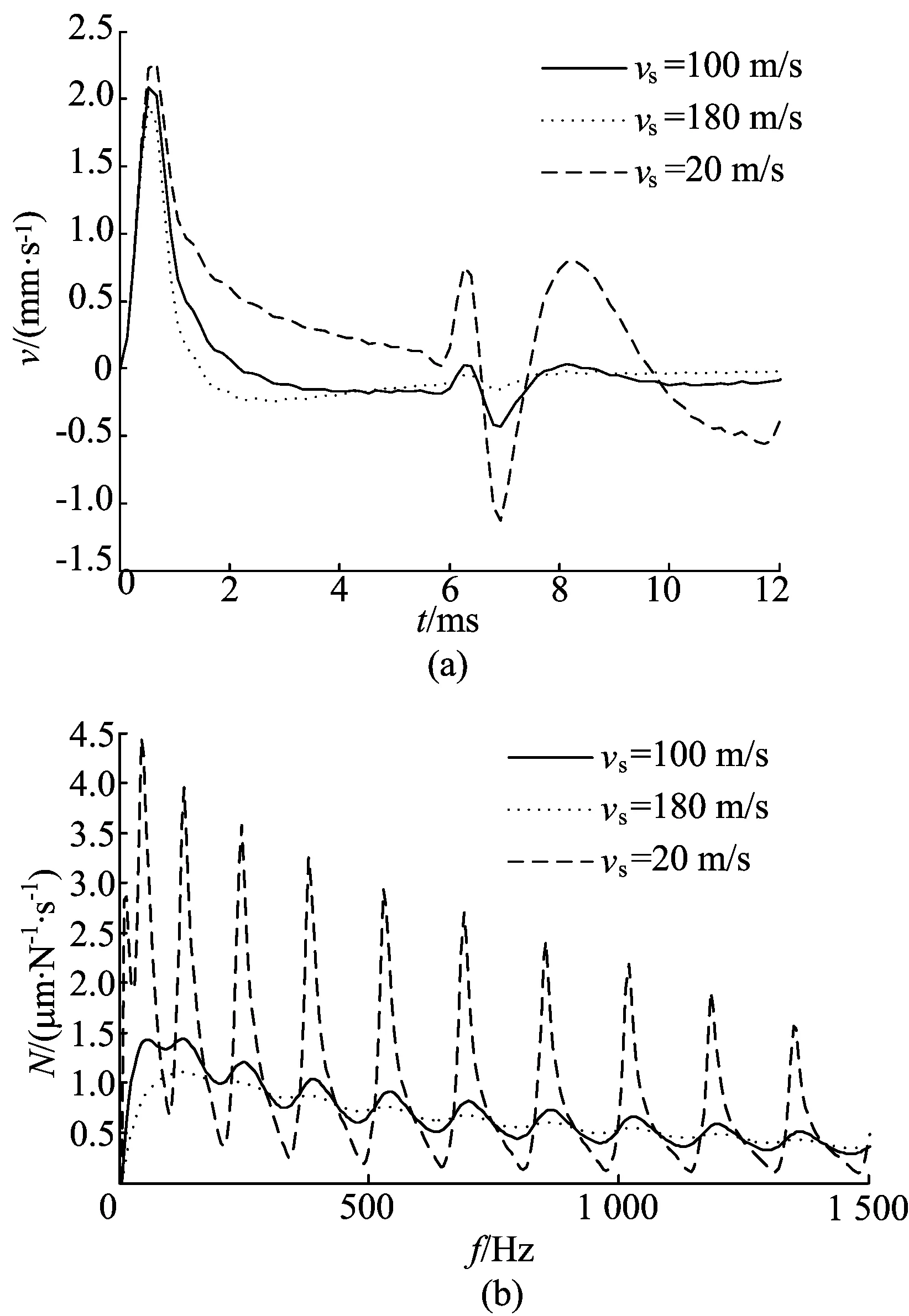
圖7　不同剪切波速橫向動力響應

圖7a中隨著樁周土剪切波速的增大,入射波的峰值和樁底反射減小。此外,入射波峰值過后,剪切波速vs很小(20 m/s)時,樁頂的橫向動剛度也非常小,樁周土對樁頂的橫向動力響應影響不大,所以速度曲線在入射波回復過后一直位于零刻度線上方;隨著vs的增加,樁周土變硬,vs=100 m/s及vs=180 m/s的速度曲線均在入射波回復過后位于零刻度線下方。圖7b中的導納曲線同樣也反映了樁頂橫向動剛度的大小及樁-土系統的阻尼特性。

6結論

本文采用Timoshenko梁模型,考慮了橫向振動下剪切作用的影響;從基本的理論方程出發，通過數學演算得到頻域內樁-土系統速度的解析解,比差分法的結果[10]具有更好的適應性;通過快速Fourier逆變換得到的時域樁頂速度曲線和速度導納曲線,顯示Timoshenko梁模型下的速度曲線與工程樁實測曲線吻合良好,速度導納曲線在正常范圍內曲線光滑,相鄰峰頻差Δf基本相等,頻散較小;將樁底邊界條件設為鉸接、自由和固定3種情況,得到樁徑比較大時,3種結果非常接近的結論;設置不同的參數,在頻域和時域內對樁頂橫向振動響應進行分析,得到的結論有利于進一步對橫向振動理論的研究,其更接近于工程實際低應變橫向測樁的結果,能夠輔助工程中低應變橫向測樁的曲線判斷。

[參考文獻]

[1]劉東甲,王建國.均勻土中有限長樁瞬態橫向動力響應[J].工程力學,2003,20(6):160-165.

[2]奚亞男,劉東甲,高云.完整樁橫向瞬態振動響應的數值模擬[J].合肥工業大學學報:自然科學版,2009,32(8):1233-1236.

[3]龍麗麗,劉東甲,蔣紅.水平瞬態荷載下基樁的動力響應分析[J].合肥工業大學學報:自然科學版,2012,35(7):951-956.

[4]胡安峰,謝康和,肖志榮.水平荷載下單樁動力反應分析[J].浙江大學學報:工學版,2003,37(4):420-425.

[5]胡安峰,謝康和,肖志榮.層狀土中考慮剪切變形的單樁水平振動解析解[J].浙江大學學報:工學版,2005,39(6):869-873.

[6]Redddy J N,Wang C M,Lee K H.Relationships between bending solutions of classical and shear deformation beam theories[J].International Journal of Solids and Structures,1996,34:3373-3384.

[7]Redddy J N,Wang C M.An overview of the relationships between solutions of the classical and shear deformation plate theories[J].Composites Science and Technology,2000,60:2327-2335.

[8]陳镕,鄭海濤,薛松濤,等.無約束Timoshenko梁橫向沖擊響應分析[J].應用數學和力學,2004,25(11):1195-1202.

[9]陳云敏,王宏志.回傳射線矩陣法分析樁頂橫向動力響應[J].巖土工程學報,2002,24(3):271-275.

[10]龍麗麗,劉東甲,盧志堂,等.基于Timoshenko梁模型的完整樁瞬態橫向振動模擬計算[J].合肥工業大學學報:自然科學版,2011,34(3):403-407.

[11]趙淳生.從測量的速度導納識別振動系統的模態參數[J].南京航空航天大學學報,1985(4):64-79.

[12]倪振華.振動力學[M].西安:西安交通大學出版社,1989:367-376.

[13]方同,薛璞.振動理論及應用[M].西安:西北工業大學出版社,1998:236-239.

[14]劉東甲.縱向振動樁側壁切應力頻率域解及其應用[J].巖土工程學報,2001,23(5):544-546.

[15]劉東甲,王建國.瞬態橫向振動樁的Winkler參數[J].巖土力學,2003,24(6):922-926.

[16]劉東甲,盧勤海,陳曉龍,等.層狀土中多缺陷樁的導納曲線計算及初步應用[J].水文地質工程地質,2001(6):18-19.

(責任編輯張淑艷)

Semi-analytical solution for transient lateral vibration of integrate piles based on Timoshenko beam model

LONG Li-li1,LIU Dong-jia2,JIANG Hong1

(1.Dept. of Municipal Engineering, Anhui Water Conservancy Technical College, Hefei 231603, China; 2.School of Resources and Environmental Engineering, Hefei University of Technology, Hefei 230009, China)

Abstract:Using the dynamical and mathematical models of lateral vibration of pile-soil system under Timoshenko beam model, an analytical solution of the velocity of lateral vibration in frequency domain was derived by Laplace transforming, and the velocity of pile head in time domain was worked out through fast inverse Fourier transforming. According to the test pile parameters, the curves of velocity admittance and pile head velocity were plotted to show the features of velocity admittance curves of Timoshenko beam model and Bernoulli-Euler beam model. The theoretical velocity curves of the two model piles and the real velocity curves of test piles were also compared to analyze the impact of variant parameters on the dynamical response of pile head. It is shown that the results of Timoshenko beam model are more approximate to the observation in low strain integrity testing than those of Bernoulli-Euler beam model. The semi-analysis method can solve the response of pile-soil system in frequency domain and has strong adaptability and high accuracy.

Key words:Timoshenko beam; transient lateral dynamic response; transfer function; admittance curve

中圖分類號:TU473.16

文獻標識碼：A

文章編號：1003-5060(2016)03-0368-06

doi:10.3969/j.issn.1003-5060.2016.03.017

作者簡介：龍麗麗(1982-),女,湖南汨羅人,安徽水利水電職業技術學院講師;劉東甲(1957-),男,安徽樅陽人,合肥工業大學教授,碩士生導師.

基金項目：安徽省高等學校優秀青年人才基金資助項目(2012SQRL244);廣東省公路管理局科技資助項目(粵公研2011-21);廣東省交通廳科技資助項目(2009-02-020);安徽省國土資源廳科研資助項目(2010-g-32)和安徽省高校自然科學研究資助項目(KJ2016A289)

收稿日期：2015-01-14；修回日期：2015-02-09