高壓下鉬的聲子色散的改進分析型嵌入原子法研究*

張曉軍，王安祥 ，高 賓，陳長樂

(1.西安工程大學理學院，陜西西安 710048; 2.西北工業大學陜西省凝聚態結構與性質重點實驗室，陜西西安 710072)

1 引 言

聲子色散關系是研究固體材料物理性質如比熱、熱導、超導、聲速、聲-電相互作用的重要信息[1]。此外，高壓下聲子譜中的負頻模式是評判固體材料結構相變的重要依據[2]。因此固體聲子色散關系的實驗和理論研究一直吸引著眾多科研工作者[3-4]。對于金屬或合金在常壓下的聲子色散關系已存在大量的實驗和理論研究結果。近年來，人們趨于對特殊條件下(如高溫和高壓)聲子色散的研究。實驗方面，把金剛石壓砧技術和非彈性X射線散射技術或非彈性中子散射技術相結合來測量高壓下固體的聲子色散關系[5-6]。另一方面，試圖從理論上重現這些實驗結果或預言高壓下的聲子色散關系。Fang等[7]利用密度泛函理論在準諧和近似下計算了壓強分別為23和55 GPa時金屬銥沿對稱方向上的聲子譜。Hu等[8]利用第一原理計算了不同壓強下金屬鈦Ti沿4個對稱方向的聲子色散曲線。這些方法物理意義深刻、明確且能提供原子間相互作用的精確信息，在計算金屬和合金的聲子色散關系方面也非常成功。但是這些方法要求計算機有相當大的計算能力，而且需要花費相當多的計算時間。同時，由于計算局限性，該方法最多只能處理上百個原子的系統，往往不能高效地描述實際的材料結構,尤其對于復雜的體系難以普遍應用。由于這些原因，研究人員開始著手利用經驗多體勢模型來研究高壓下的聲子色散關系。與第一原理計算相比，經驗多體勢模型能夠快速提供原子或分子間的相互作用信息，且能處理幾千甚至上萬個原子的龐雜系統。Kazanc等[9]曾利用經驗多體勢即Sutton-Chen式嵌入原子法(SCEAM)計算了不同壓強下鎳鈀無序合金沿[100]、[110]和[111] 3個高對稱方向上的聲子色散曲線。我們也曾用張邦維等發展的改進分析型嵌入原子法(MAEAM)模擬了高壓下金屬銅沿3個高對稱方向和4個低對稱方向上的聲子色散曲線[10]。然而，這些結果都沒有相應的實驗數據相佐證，難于說明經驗多體勢是否能合理描述高壓下原子間的相互作用。本研究把張邦維等發展的改進分析型嵌入原子法模型與晶格動力學理論相結合，模擬高壓下金屬鉬(Mo)沿3個高對稱方向上的聲子色散曲線，并和對應的實驗結果進行比較。

2 改進分析型嵌入原子法模型

在重現或預測固體材料聲子色散關系的計算中，原子之間的相互作用勢是必不可少的。經常采用的兩體勢有Morse勢[11]和Murrell Sorbie勢[12]，多體勢模型有密度泛函理論(DFT)[13]、嵌入原子勢模型(EAM)[14]和緊束縛理論(TBT)[15]等。其中，由Zhang等[16-17]發展的改進分析型嵌入原子法模型已成功地計算了面心立方金屬的界面能[18]、晶界能[19]以及體心立方金屬的空位遷移能[17]等。改進分析型嵌入原子法的基本公式為[16-17]

式中:Et是系統的總能量，F(ρi)是在除第i個原子外的其他原子組成的基體中再嵌入第i個原子的嵌入能，僅是其他原子在第i個原子所在處產生的背景電子密度ρi的函數，其中f(rij)為單個孤立原子的球型電子密度分布函數，rij是第i個原子和第j個原子間的距離；φ(rij)是第i個原子和第j個原子間的相互作用能；M(Pi)是修正項，表示原子電子密度非球型對稱分布所引起的系統總能量的變化。嵌入函數F(ρi)、原子間的相互作用勢φ(rij)、修正項M(Pi)和電子密度函數f(rij)采用如下形式[16-17]

式中:下標“e”表示平衡狀態，re表示在平衡狀態下純元素晶體中原子的最近鄰距離，其他模型參數如F0、n、α、ks(s=-1～4)見表1。

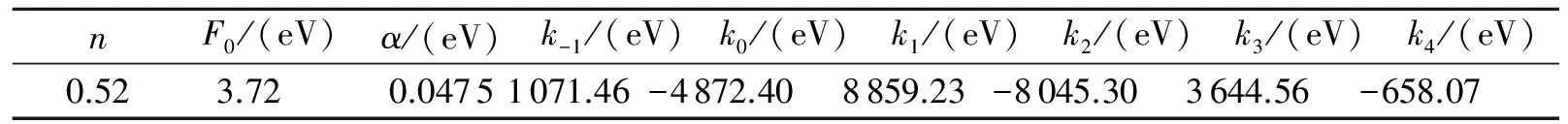
表1 金屬鉬的模型參數Table 1 The model parameters of metal Mo

3 晶格振動模型

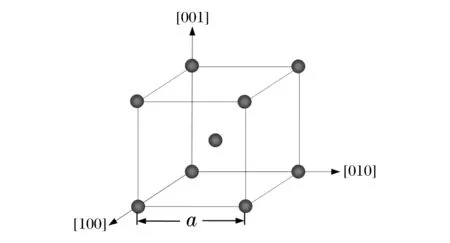
圖1 體心立方晶體結構 Fig.1 Bcc crystal structure

常溫常壓下，金屬鉬屬體心立方結構，其晶體結構如圖1所示，晶格常數為a。在晶體結構中設坐標原點處的原子為參考原子n，根據晶格動力學理論[20]，參考原子n的振動方程為

(8)

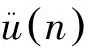
(9)

求解(8)式，可得

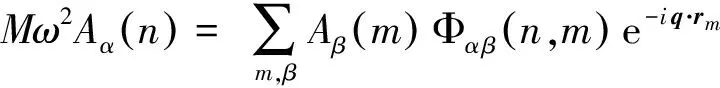
(10)

(11)

顯然，(11)式是A(n)的3個線性齊次方程，因為晶格振動總是存在的，故A(n)有非零解的條件是

|Dα β(n,m)-δα βω2(q)|=0

(12)

通過聯立(1)式、(9)和(12)式，就可以得到體系的振動頻率ω(q)和波矢之間的關系，即聲子色散關系。

4 模擬方法和結果分析

在晶格動力學理論和改進分析型嵌入原子法的框架下，采用數值計算的方法模擬了高壓下金屬鉬的聲子色散曲線。在模擬過程中，選取8a×8a×8a的晶塊作為模擬單元，其中包括坐標原點在內的4a×4a×4a晶塊作為內部單元，其余原子為外部單元，外部單元是為了確保內部單元邊界處和近邊界處的原子周圍有足夠多的近鄰原子與之相互作用，同時假設所有的原子滿足三維周期邊界條件。選取對勢函數的截止距離為0.626 nm，應用Matlab語言編輯計算機程序計算參考原子與其他原子之間的原子力常數和動力學矩陣元，把這些值代入久期方程((12)式)獲得不同波矢所對應的聲子頻率值，具體的計算細節可參考文獻[21]和文獻[22]。在計算不同壓強下的聲子色散關系時，采用Rose-Vinet[23-24]方程來控制加載在體系上的靜壓力。根據Rose-Vinet方程，金屬鉬的壓強和壓縮的關系可表示為

(13)

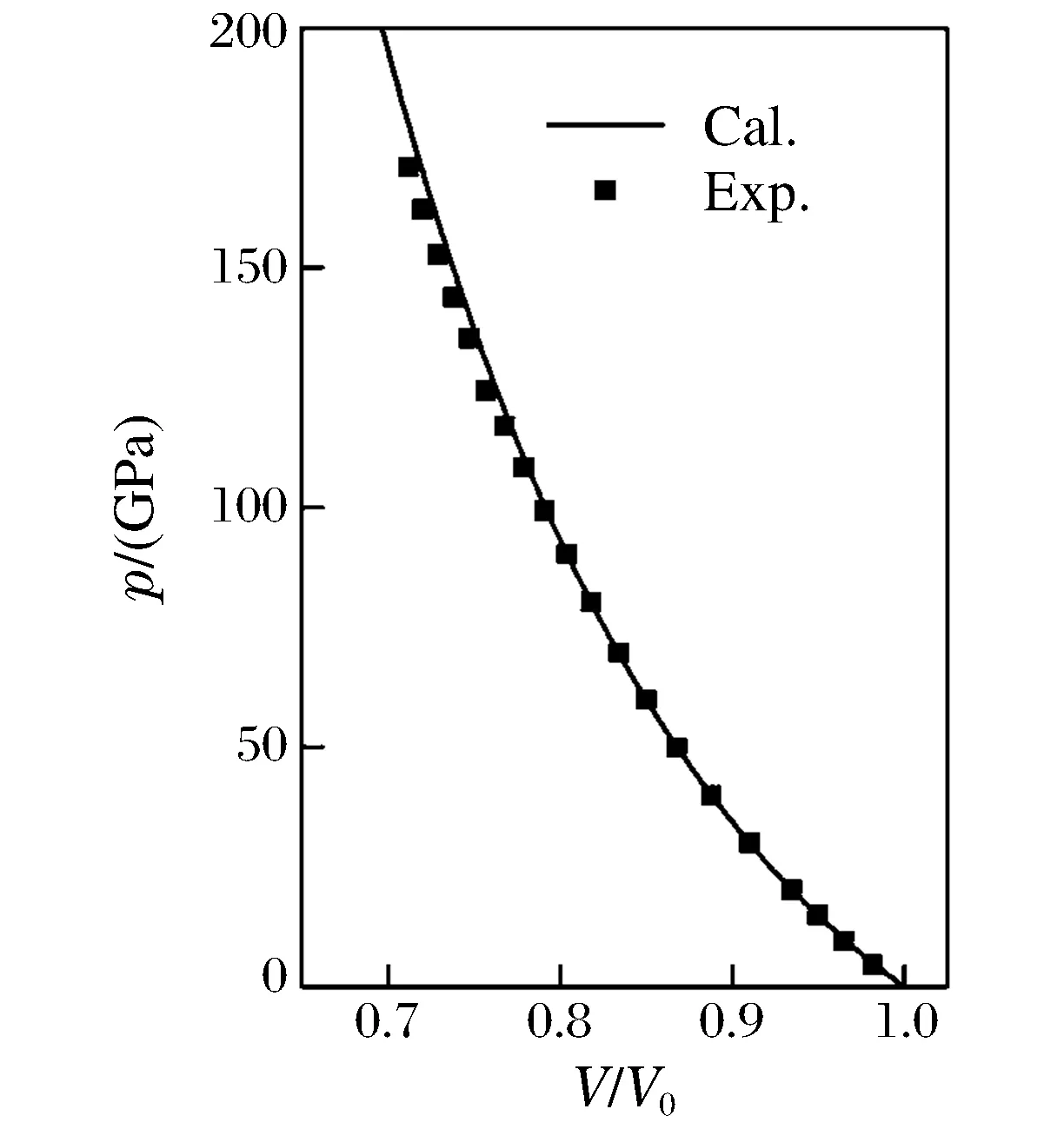
圖2 金屬鉬的壓強和體積間的關系 Fig.2 Pressure versus volume for Mo

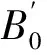
由MAEAM模型所計算的壓強分別為0.1 MPa、17 GPa和37 GPa時金屬鉬沿[00ζ]、[0ζζ]和[ζζζ] 3個高對稱方向的聲子色散曲線如圖3、圖4、圖5所示，其中實線為模擬值，實心圓點為實驗值[26-27]，群論符號Γ、H、P′、P和N表示體心立方晶格布里淵區中的不同對稱點，符號L和T分別表示縱振動模和橫振動模，ζ=q/qmax是簡約波矢。根據晶格動力學理論，體心立方布拉菲晶胞會產生3個聲子振動支，其中2個為橫波聲學振動支，1個是縱波聲學振動支，由于四重和六重軸對稱性，2個橫波聲學振動支往往會在某些振動方向上兼并為1個橫波振動支，如圖3、圖4、圖5所示，這些圖像和現在的計算結果相符合。從圖3可以看出，在常壓下(0.1 MPa)，我們的計算結果整體上和實驗結果相一致，包括一些布里淵邊界點，例如T[00ζ]和L[00ζ] 振動支中的H點，T1[0ζζ]和T2[0ζζ]振動支中的N點。在L[00ζ]振動支中簡約波矢ζ在0.3～0.6之間，T[ζζζ]振動支中ζ在0.3～0.9之間，L[0ζζ]振動支中ζ在0.3～0.5之間。計算結果與實驗結果在數值上有些偏差，但所對應色散曲線的形狀卻非常相似(圖3)。壓強p=17 GPa時，色散曲線的理論計算實線和實驗點線整體一致，特別在低頻附近(圖4)。與常壓下聲子色散曲線相比，在壓強為17 GPa時的色散曲線中，頻率偏差主要出現在T[00ζ]和L[00ζ]振動支中的H點、T[ζζζ]和L[ζζζ]振動支中的P點以及T1[0ζζ]和L[0ζζ]振動支中的N點附近，最大偏差不超過10.8%。壓強p=37 GPa時，L[00ζ]振動支的色散曲線和實驗結果基本吻合，其他方向上色散曲線的形狀和常壓以及17 GPa時的結果非常相似，只是頻率略有上移，遺憾的是只有L[00ζ] 振動支的實驗結果與之相比較，而缺少其他振動支的實驗數據。從上面的分析可看出，我們的計算結果均與實驗結果基本吻合，只是數值上有較些差異。考慮到計算結果是在諧和近似下所得，而實驗結果并不能忽略非諧和效應，因此二者之間存在差異是合理的。這表明MAEAM模型可以合理描述常壓和高壓下原子之間的相互作用。

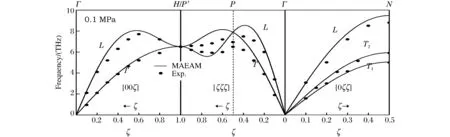
圖3 常壓下鉬的聲子色散曲線 Fig.3 Phonon dispersion curves of Mo under normal pressures

圖5 壓強p=37 GPa時鉬的聲子色散曲線 Fig.5 Phonon dispersion curves of W at 37 GPa

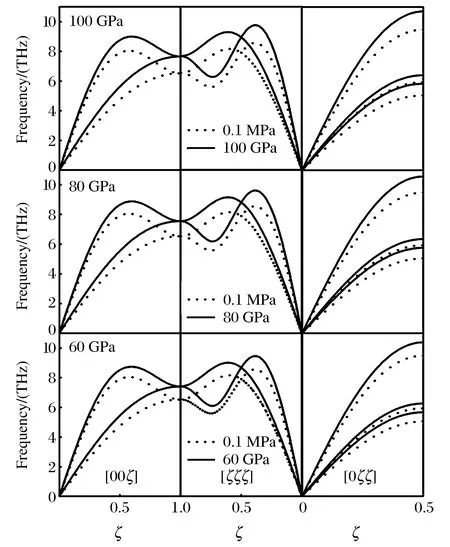
圖6 不同高壓下鉬的聲子色散曲線 Fig.6 Phonon dispersion curves of Mo under different high pressures

圖6是壓強分別為60、80和100 GPa時的聲子色散曲線，其中固體實線是高壓下的色散曲線，為了方便比較，在圖6中我們還添加了常壓下的色散曲線，并用點線表示。從圖6中可以看出，常壓下以及高壓下(p=60、80和100 GPa)的聲子色散曲線非常相似，這種相似性并不驚奇，因為金屬鉬保持體心立方結構直到我們所考慮的最大壓強范圍內(100 GPa)。高壓下所有振動支的振動頻率均高于常壓下的振動頻率，與常壓聲子色散相比，p=60 GPa時的最大振動頻率增加了14.3%，p=80 GPa時增加了16.3%，p=100 GPa時增加了18.1%。在所有的振動支中的振動頻率均隨壓強的增大而增大。在不考慮質量、相互作用距離和結合能所引起的差別時，這些現象和高壓下體心立方金屬鎢[28]和鉭[29]的計算結果相一致。

為了近一步說明聲子頻率和壓強之間的關系，模擬了金屬鉬的T2[0ζζ]和L[00ζ]振動支中簡約波矢分別為0.2、0.5、0.8 和1.0時的聲子色散頻率隨壓強的關系，如圖7所示。從圖7可以看出，在兩個振動支上，4個簡約點的聲子頻率均隨壓強的增加而增加。在相同振動支中各簡約點的聲子頻率和壓強之間的關系基本相同。因此，如果想知道聲子色散和壓強之間的關系時，我們只要考慮某一振動方向上某一簡約點的振動情況即可。此外，在40～100 GPa范圍內，各個簡約點的頻率和壓強基本上呈線性關系。

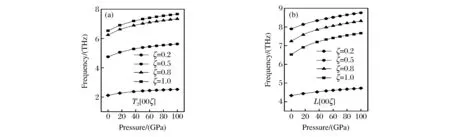
圖7 不同簡約波矢的聲子頻率和壓強之間的關系 Fig.7 Phonon frequencies versus pressures at different reduced wave vectors

5 結 論

應用改進分析型嵌入原子法模型計算了不同高壓下金屬鉬的原子力常數和動力學矩陣，重現了3種壓強下金屬鉬沿3個高對稱方向上聲子色散的實驗結果，預測了鉬在壓強分別為60、80和100 GPa時的聲子色散曲線。得到以下結果：(1) 壓強分別為0.1 MPa、17 GPa和37 GPa時金屬鉬的聲子色散曲線的模擬結果和實驗值符合較好，特別在低頻附近二者幾乎一致。(2) 在壓強分別為p=60、80和100 GPa時所預測的聲子色散曲線和常壓下聲子色散曲線的形狀都非常相似，且隨著壓強的增大各振動支的振動頻率均依次增大。(3) 不同振動支上不同簡約點的聲子頻率均隨壓強的增加而增加，在40～100 GPa范圍內，所考慮的各個簡約點的頻率和壓強基本上呈線性關系。(4) 上述方法也可用于其他金屬或合金在高壓條件下聲子色散關系的計算和研究。

[1] XIE Y,ZHANG J M.Atomistic simulation of phonon dispersion for body-centred cubic alkali metals [J].Can J Phys,2008,86(6):801-805.

[2] WANG Y,HECTOR L G,ZHANG H,et al.Thermodynamics of the Ceγ-αtransition:Density functional study [J].Phys Rev B,2008,78(10):104113.

[3] WONG J,KRISCH M,FARBER D L,et al.Crystal dynamics of fcc Pu-Ga alloy by high-resolution inelastic X-ray scattering [J].Phys Rev B,2005,72(6):064115.

[4] ADITYA M V.Phonon dispersion in equiatomic Li-based binary alloys [J].Chin Phys Lett,2008,25(2):654-657.

[5] DANIEL L F,KRISCH M,ANTONANGELI D,et al.Lattice dynamics of molybdenum at high pressure [J].Phys Rev Lett,2006,96(4):115502.

[6] MITTAL R,CHAPLOT S L,CHOUDHURY N,et al.Inelastic neutron scattering,lattice dynamics and high-pressure phase stability in LuPO4and YbPO4[J].J Phys-Condens Mat,2007,19(44):6202.

[7] FANG H,LIU B,GU M.High-pressure lattice dynamic and thermodynamic properties of Ir by first-principles calculation [J].Physica B,2010,405(2):732-737.

[8] HU C E,ZENG Z Y,ZHANG L.Theoretical investigation of the high pressure structure,lattice dynamics,phase transition,and thermal equation of state of titanium metal [J].J Appl Phys,2010,107(9):093509.

[9] KAZANC S.The effects on the lattice dynamical properties of the temperature and pressure in random NiPd alloy [J].Can J Phys,2013,91(10):833-838.

[10] ZHANG X J,CHEN C L,FENG F L.High-pressure phonon dispersion of copper by using the modified analytic embedded atom method [J].Chin Phys B,2013,22(9):096301.

[11] MORSE P M.Diatomic molecules according to the wave mechanics.Ⅱ.Vibrational levels [J].Phys Rev,1929,34(1):57-64.

[12] MURRELL J N,SORBIE K S.New analytic form for potential energy curves of stable diatomic states [J].J Chem Soc Faraday Trans,1974,70(2):1552-1556.

[13] SEBETCI A.A density functional study of bare and hydrogenated platinum clusters [J].Chem Phys,2006,331(1):9-18.

[14] DAW M S,BASKES M I.Embedded atom method:A review derivation and application to impurities,surface and other defects in metals [J].Phys Rev B,1984,29(12):6443-6447.

[15] BOYKIN T B,VOGL P.Dielectric response of molecules in empirical tight-binding theory [J].Phys Rev B,2002,65(3):035202.

[16] OUYANG Y F,ZHANG B W.Analytic embedded atom potentials for bcc metals:application to calculating the thermodynamic data of bcc alloys [J].Phys Lett A,1994,192(1):79-86.

[17] HU W Y,SHU X L,ZHANG B W.Point-defect properties in body-centered cubic transition metals with analytic EAM interatomic potentials [J].Comput Mater Sci,2002,23(1):175-189.

[18] MA F,ZHANG J M,XU K W.Theoretical analysis of interface energy for unrelaxed Ag (001)/Ni (001) twist interface boundaries with MAEAM [J].Surf Interface Anal,2004,36(4):355-359.

[19] ZHANG J M,WEI X M,XIN H,et al.Atomic scale calculation of energies of Cu (001) twist boundaries [J].Chin Phys,2004,14(5):1015-1020.

[20] DOVE M T.Introducton to lattice dynamics [M].New York:Cambridge University Press,1993.

[21] KAZANC S,OZGEN S.Pressure effect on phonon frequencies in some transition metals:A molecular dynamics study [J].Physica B,2005,365(1/2/3/4):185-192.

[22] KAZANC S,OZGEN S,ADIGUZEL O.Pressure effects on martensitic transformation under quenching process in a molecular dynamics model of NiAl alloy [J].Physica B,2003,334(3/4):375-381.

[23] ROSE J H,SMITH J R,GUINEA F,et al.Universal features of the equation of state of metals [J].Phys Rev B,1984,29(6):2963-2969.

[24] VINET P,ROSE J H,FERRANTE J,et al.Universal features of the equation of state of solids [J].J Phys-Condens Mat,1989,1(11):1941-1963.

[25] MAO H K,BELL P M,SHANER J W,et al.Specific volume measurements of Cu,Mo,Pd,and Ag and calibration of the rubyR1fluorescence pressure gauge from 0.06 to 1 Mbar [J].J Appl Phys,1978,49(6):3276-3283.

[26] WOODS A D B,CHEN S H.Lattice dynamics of molybdenum [J].Solid State Commun,1964,2(8):233-242.

[27] FARBER D L,KRISCH M,ANTONANGELI D,et al.Lattice dynamics of molybdenum at high pressure [J].Phys Rev Lett,2006,96(11):115502.

[28] ZHANG X J,CHEN C L.Pressure dependence of phonon dispersion in bcc tungsten [J].Chin J Phys,2013,51(2):359-367.

[29] TAIOLI S,CAZORLA C,GILLAN M J,et al.Melting curve of tantalum from first principles [J].Phys Rev B,2007,75(21):214103.