新課程理念下合情推理在數學學習中的作用
?
新課程理念下合情推理在數學學習中的作用
■田靜
所謂合情推理,簡單地說,就是合理地猜測,不少數學結論及相應的證明也是靠合情推理才得以發現的。世界上許多著名的科學家、教育家都十分倡導合情推理,給予其積極的評價。牛頓就說過:“沒有大膽的猜測,就沒有大膽的發現。”新課程教育理念要求培養學生的直覺思維,引導學生大膽猜測,注意其對特殊情況的觀察,導出一般性的數學結果或一般性的解題方法。與合情推理相關的內容體現在《新課程標準》推理與證明部分,它要求學生通過運用合情推理探索與發現數學結論和解題思路,體會合情推理在數學發現中的作用。
一、在數學探索和發現中運用合情推理,有助于培養學生的創新思維能力
重視引導學生在學習中運用合情推理去發現解題途徑和方法,可以模擬數學家的思維活動,有助于引導學生進行“似真性”地發現定理(公式),以及構想定理(公式)證明的方法,是學習中培養學生創造性思維能力的重要途徑。
例如:高中數學“等差數列通項公式”的推導,可以從等差數列特點及定義來引入。
定義:n≥2時,有an-an-1=d,則:
a2=a1+d;
a3=a2+d=a1+2d;
a4=a3+d=a1+3d;
a5=a4+d=a1+4d;
……
猜測并寫出an=?
很顯然,由歸納推理得到的結論具有似真性,它必須經過論證推理之后才能確認其正確性。課本必修5是這樣安排的,在學生的學習過程中,這樣的引導培養了學生的創新思維能力。
二、在概念、定理、公式學習中運用合情推理,有助于調動學生學習積極性
數學概念是整個數學知識結構的基礎,學生在進行數學概念的學習時,要讓學生“感知”新教材,在“感知”的過程中可以引導學生進行合情推理。讓學生在學習中模擬數學家的思維過程,運用歸納、類比、猜想等合情推理推斷結論,從而調動學生學習數學的積極性。

三、運用合情推理,可以發展學生思維的靈活性


由此可知,所求的和恰好是上述復數(1+z)n的實部。
又(1+z)n=(1+cosθ+isinθ)n

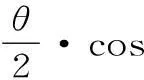
四、運用合情推理,可以培養學生思維的批判性
例如:設f(x)=ax2+bx+c(a≠0),已知,當|x|≤1時,|f(x)|≤1恒成立,證明:當|x|≤2時,|f(x)|≤7恒成立。

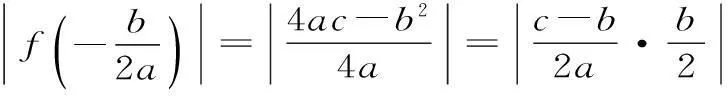
總而言之,操作探究是創新的基本技能,而合情推理則是創新思維的火花。我們在學習中不僅要充分挖掘新教材資源,更要體現數學中的探索、推理的思想,鍛煉自己的思維強度,擦出思維的火花,用火花去點燃學習激情。
作者單位:湖北省荊門市掇刀石中學

