不從起點植樹會怎樣？

李凱

植樹問題是新人教版《數學》五年級上冊第七單元《數學廣角》中的內容，這類問題變化多樣，學生容易混淆。如何能幫助學生把這類問題理解清楚呢？筆者認為還是要回到問題的源頭上，從植樹時不考慮起點開始探究，借助學生已有的學習經驗引導學生理解植樹問題。

一、由“不從起點植樹”引發的思考

1.不從起點植樹，棵數等于間隔數（學生已有經驗）

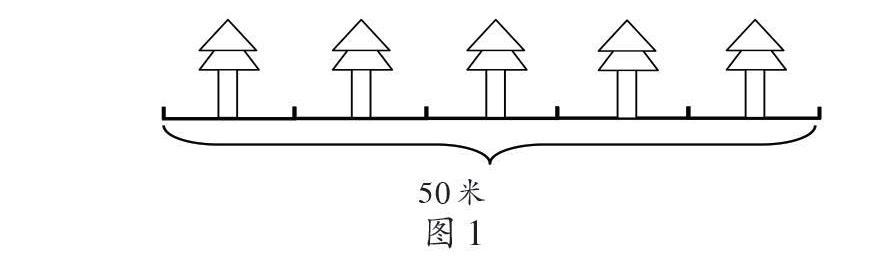
一段50米的小路，每隔10米種一棵樹，可以種多少棵？學生根據以往的學習經驗50米里面有5個10米，因此可以種5棵樹，應該說學生這樣的學習經驗并沒有錯，如圖1。

2.“不從起點植樹”與“兩端都植樹”的聯系

如果繼續把小樹向左右兩端平移，會得到什么結果呢？顯而易見，這樣會出現一端栽一端不栽的情況，如圖4、圖5。結論依然成立。按照每間隔10米種一棵的要求，此時還可以在起點或者是終點再種一棵樹，這樣棵樹就等于間隔數+1了。

只是這個時候線段兩個端點上的樹去掉了，也可以想象成在兩個端點上栽花，如圖6。

因此在一條線段上植樹，是否從起點開始植樹是十分重要的限定條件，它是區分新舊知識和經驗的重要節點。據此可以得到這樣的關系，如圖7。

3.在圓周上植樹需要考慮起點嗎？

從教材的示意圖（圖8）中可以看出，在圓形的路線上植樹，棵數與間隔數相等。問題是在圓形線路上植樹需要考慮起點的位置嗎？

我們用鐘面為例，將圓周平均分成12等份，如果間距是3個等份，顯而易見可以種4棵樹。用小圓點表示樹，如果在12點的位置種第一棵樹，則后面的3棵樹分別應該在3點、6點和9點的位置，如圖9。如果在一點的位置種下第一棵樹，則后面3棵樹的位置會以此向后移動一個刻度，如圖10，雖然起點的位置改變了，但是結論依然是4棵。可見在圓周上植樹是不用考慮起點位置的，無論起點在哪里，棵樹都等于間隔數。

4.在圓形路線上的結論推廣到其他封閉路線

如果是在長方形或正方形的周界上植樹，棵數是不是還等于間隔數呢？我們可以試驗一下。以正方形為例，我們把正方形的邊長看成4，間距設為2。如果正方形的四個頂點上種樹如圖11，那么有8個間隔對應有8棵樹。如果把這8棵樹按順時針移動相同的距離，就會出現頂點上不種樹的情況如圖12，這時依然有8個間隔對應8棵樹。

因此在封閉路線上以任意一個點為起點，都能夠得到間隔數等于棵樹的結論，無論頂點上是否種樹都不影響到這個結論。

二、對植樹問題的知識結構調整

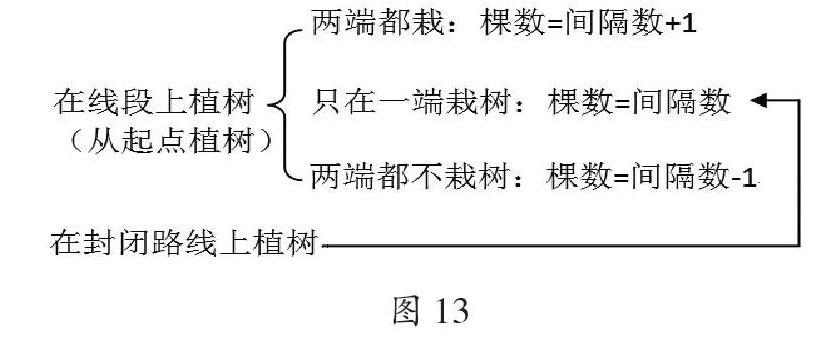
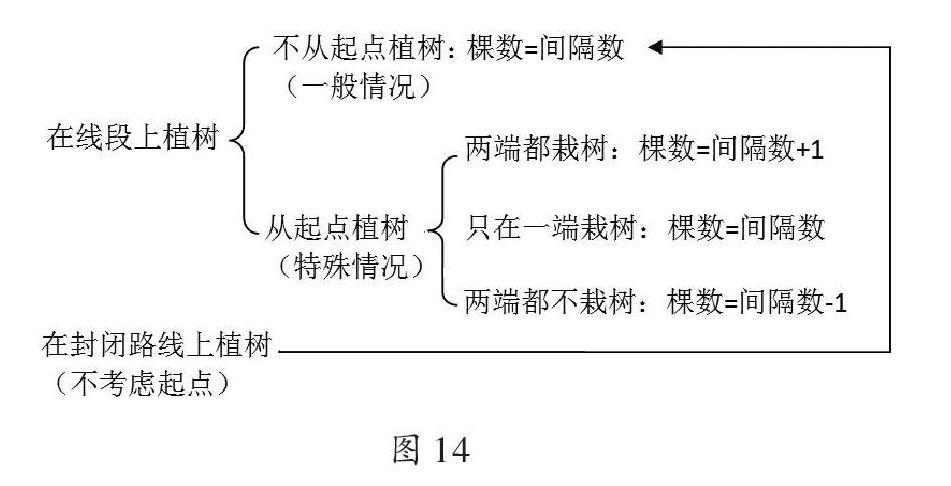
圖13是原來植樹問題的知識結構。從圖中可以看出在封閉路線上植樹的問題可以轉化成在線段上植樹問題中“一端栽，一端不栽”的情況來考慮，但是這兩個問題的前提是不一樣的，一個要考慮起點，一個不考慮起點，它們只是結論恰好相同而已。實際上在封閉路線上植樹應該與學生原有的學習經驗對應起來，那就是有幾個間隔就有幾棵樹，不考慮起點。因此可以將原有的知識結構圖調整一下如圖14，這樣學生對于植樹問題就比較明晰了，考慮起點時，用原有經驗得到間隔數，再根據要求對間隔數進行調整得到種樹棵數，不考慮起點時，則運用原有經驗，間隔數直接等于種樹棵數。

可能有人會這樣認為：既然結論相同，原有的知識結構也是成立的，不這樣調整似乎也沒有什么問題。事實并不是這樣，首先，不應該把不同類型的問題混為一談；其次，分清楚知識結構也有利于我們認識到問題的本質，簡化解決問題的思路和步驟。

學生的配套練習中有一道題：全班52名同學在操場上做游戲，大家圍成正方形，每邊人數相等，四個頂點都有人，相鄰兩個同學之間相隔0.8米，求圍成的正方形的邊長是多少米。按照一般的解法是要考慮起點的，因為題目也限定了每個頂點都有人。先算每邊人數的時候實際上是轉化成了兩端都種樹的情況，并涉及到四個頂點重復計算問題還需要倒推，這樣算起來就會比較復雜。如果按照現在的思路，在封閉路線上植樹，不考慮起點，52個人就有52個間隔，無論四個頂點上有沒有人，每條邊上的間隔數都是一樣的，這樣算邊長不就很簡單了嗎。而且13+1就可以得到每邊人數，比起之前的方法是不是簡便很多呢。

一般的解法：先求每邊的學生人數（52-4）÷4+2=14（人），再求每邊的間隔數14-1=13（個），最后求邊長13×0.8=10.4（米）。

現在的解法：先求每邊的間隔數52÷4=13（個），再求邊長13×0.8=10.4（米）。

從圖13可以清楚看到，原有的知識結構與學生已有的數學經驗沒有什么聯系，全部需要學生自己建構。如果采用圖14的知識結構，更多的學習經驗可以直接繼承，需要做出調整的部分減少，這樣學生的學習難度就降低了。數學學習強調邏輯性和連貫性，這既是一個繼承的過程，也是一個創新的過程。

（作者單位：武漢小學）