一種基于STFT的欠采樣測頻技術

呂　昊，羅　明

(西安電子科技大學，西安 710071)

?

一種基于STFT的欠采樣測頻技術

呂昊，羅明

(西安電子科技大學，西安 710071)

摘要：在現代電子戰中，數字測頻技術的發展至關重要。對短時傅里葉變換(STFT)數字信道化技術進行了原理分析和理論仿真，然后研究了欠采樣技術，并提出了將STFT信道化與欠采樣結合使用的測頻方法，并以正交雙通道延遲解模糊為例，仿真驗證方法的可行性。

關鍵詞：測頻；短時傅里葉變換；數字信道化技術;欠采樣

0引言

在現代電子戰中，寬帶數字接收機的地位越來越重要，而在數字接收機的設計中，信道化技術又是其中至關重要的一部分[1]。數字信道化技術兼有數字系統穩定、靈活的特點和信道化技術截獲概率高、實時性好、能同時處理多信號的優點，因而被廣泛應用[2]。本文研究的短時傅里葉變換(STFT)就是一種適合于寬帶數字接收機的算法。不過，隨著現代戰場信號環境的復雜化和雷達技術的快速革新，數字信道化技術也面臨著更多的挑戰。

欠采樣可以解決采樣速率與信號處理速率不匹配的問題，可以降低運算速度，減少運算量。對欠采樣頻率估計方法的研究，主要體現在對解模糊算法的研究，欠采樣技術對于數字偵察接收機來說具有很大的應用意義。

1STFT數字信道化測頻原理

STFT技術可用來實現數字信道化，它是研究非平穩信號的常用方法，能同時在時域和頻域反映信號的特征，便于對信號進行較為直觀的時頻分析，并且對信號的局部特性有著較強的描述能力[3]。

下面對STFT的基本思想進行說明：首先確定合適的窗函數，設定好窗寬與快速傅里葉變換(FFT)點數，在一個時間窗內可以等效認為信號是平穩信號，用快速傅里葉變換FFT來描述當前窗內信號的頻率分布。讓窗函數沿著時間軸滑動，就可以依次得到不同窗內輸入信號的頻率分布，從而得到輸入信號頻率隨著時間變化的規律。從上述描述不難看出， STFT是隨著窗函數沿著時間軸的滑動，對信號進行了多次FFT的結果。STFT不僅可以測量信號的載頻、帶寬等頻域上的信息，還可以檢測信號的到達時間、脈寬、周期等時域上的信息。

STFT的算法模型如圖1所示。圖中選取的窗寬為N，FFT點數與窗口寬度相同,也是N，輸入的連續數字信號經過數據整理模塊后，進行加窗濾波處理，然后分段送給FFT模塊進行頻域信息分析。STFT算法可以對采樣數據進行連續不斷的頻譜分析，并實時輸出分析結果。

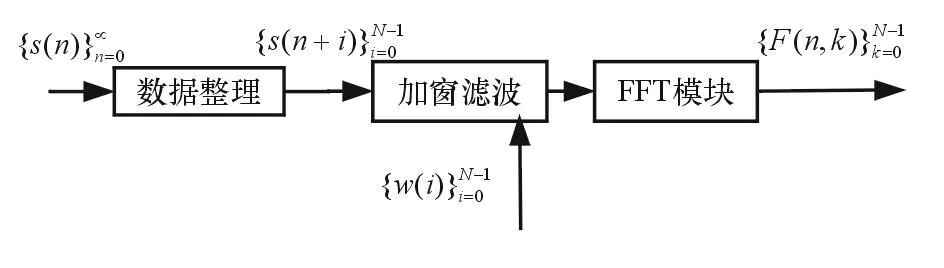
圖1　STFT的算法模型

根據上述的模型分析，推導出STFT的數學表達式:

(1)

隨著時刻點n在時間軸上的滑動，可以得到輸入信號頻率分布與時間的關系，也就是說，STFT因此具有了時頻分析能力。

如上文所述，隨著窗函數沿著時間軸的滑動，可以得到信道在不同時刻的檢測結果，根據輸入信號的到達時間與消失時間，可以計算出輸入信號時域信息，STFT參數估計流程如圖2所示。

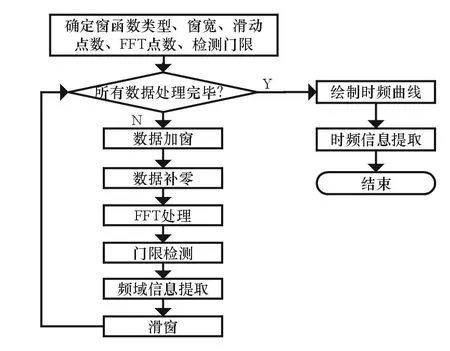
圖2　STFT參數估計流程圖

首先對輸入信號進行加窗處理，截取與窗寬長度一致的信號，按照FFT點數進行補零操作，通過FFT觀測當前時間窗內信號的頻率分布，對FFT輸出頻譜的各信道進行門限檢測，確定信號的有無，對有信號輸入的進行輸入信號的頻率確認，窗函數滑動固定的點數，分析下一時刻的信號頻率分布，直至全部數據處理完畢，根據窗函數滑動得到的每一時刻的信號頻率分布繪制信號頻率分布與時間的關系曲線，分析輸入信號的時域信息。

設輸入信號為時域完全重疊的2個線性調頻信號，采樣頻率fs=500MHz，信噪比σSNR=25dB，仿真時間T=327.68μs。

(1) 輸入雷達信號參數

信號1參數：重頻TPRI1=131.1μs，脈寬TPW1=65.54μs，起始頻率f1′=100MHz，帶寬B1=5MHz，幅度A1=3V；信號2參數：重頻TPRI2=131.1μs，脈寬TPW2=65.54μs，起始頻率f2′=120MHz，帶寬B2=4MHz，幅度A2=3V。

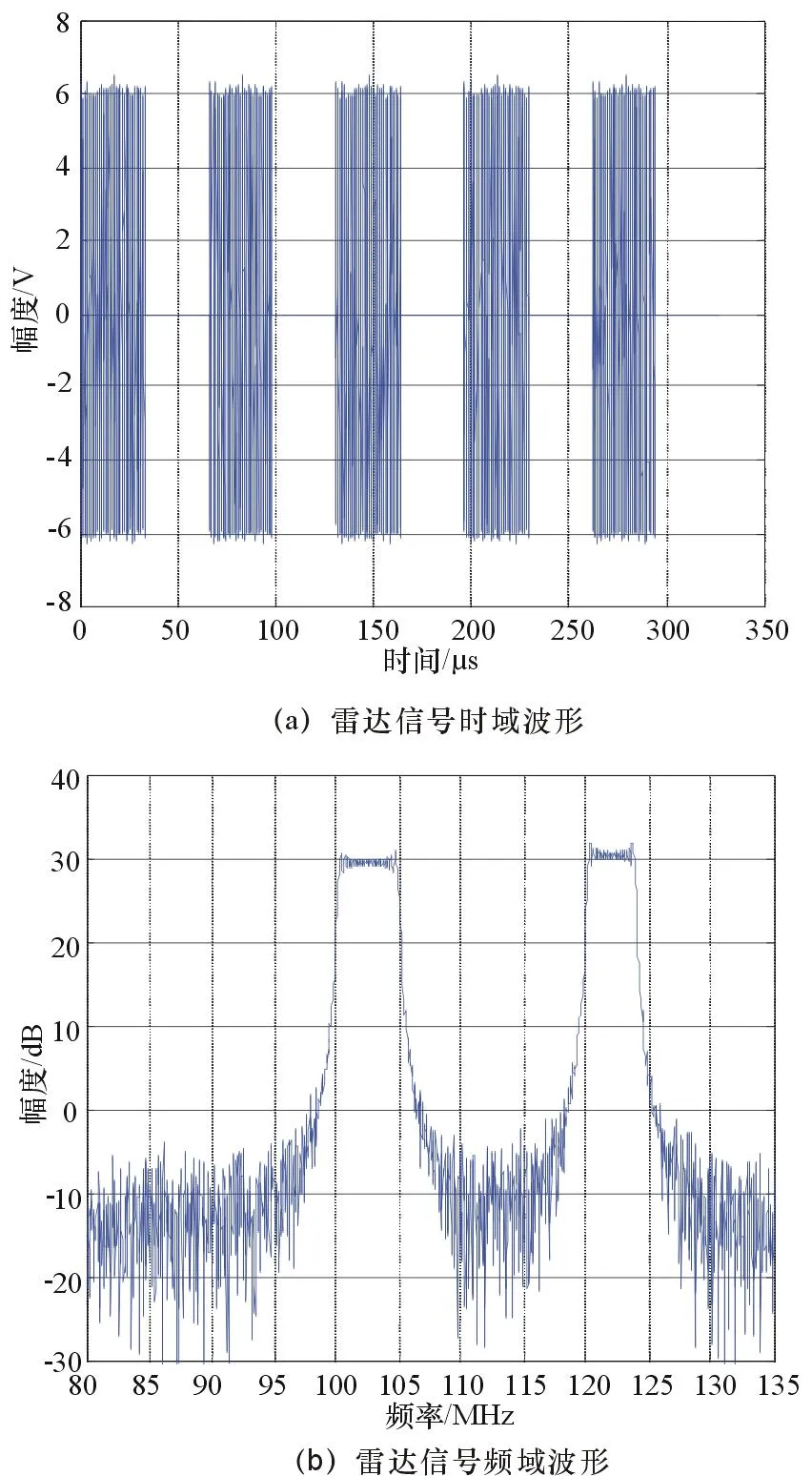
圖3　輸入雷達信號仿真

(2) STFT濾波器組參數設置

仿真中時域加的窗函數為矩形窗，窗函數寬度為1 024點，滑動點數為512點，對窗內信號做1 024點FFT，圖4為經過STFT濾波器組處理后輸出信號三維圖與等高圖。

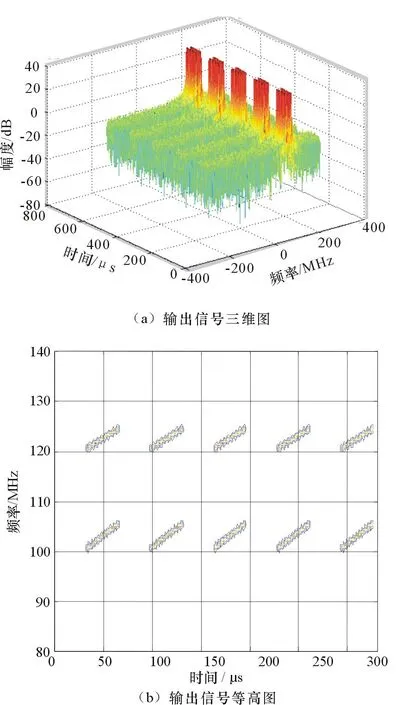
圖4　STFT濾波器輸出信號三維圖與等高圖

(3) 信號頻域參數測量

單個時間窗內FFT輸出功率譜和信號時頻分析曲線如圖5所示。

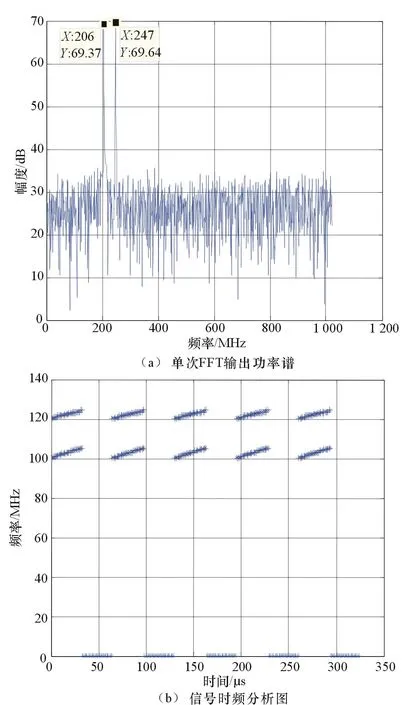
圖5　單個時間窗內FFT輸出功率譜與時頻分析曲線

從圖5的時頻分析結果可以看出，輸入信號為2個線性調頻信號，信號開始時刻峰值檢測信道分別為206和247，信號結束時刻檢測信道分別為216和255，可以估計出起始頻率：f01=205/1 024×500MHz=100.09MHz，f02=246/1 024×500MHz=120.11MHz，終止頻率：fp1=215/1 024×500MHz=104.98MHz，fp2=254/1 024×500MHz=124.02MHz，信號帶寬：B1=fp1-f01=4.89MHz，B2=fp2-f02=3.91MHz。

(4) 時域參數的測量

圖6給出了STFT滑窗第1～35次FFT濾波器輸出功率譜的監測結果。

從圖6可以看出，第1個窗函數內有信號，記為信號到達時間，第33個窗函數信號從有到無，記為結束時間，計算得到脈寬TPW=32×1.024μs=32.768μs，第2個脈沖在第65個時間窗到來，計算得到周期TPRI=64×1.024μs=65.536μs，與仿真設置脈沖時域參數相同，依據上述原則測得的脈寬、周期最大誤差為Δt。

圖6　第1～35次FFT輸出功率譜

2欠采樣測頻原理

根據奈奎斯特定理可知，采樣頻率高于信號最高頻率的2倍時，就可以從采樣信號中恢復出原始信號。而欠采樣采樣頻率低于信號最高頻率2倍的情況下對信號進行數字化[4]。欠采樣會導致頻譜的混疊，但是如果可以通過其他方式得到真實頻率經過頻譜折疊的折疊次數(即模糊數)，就可以根據欠采樣公式獲得信號頻率的真實估計，這樣就能夠通過較低的采樣率對大帶寬高頻信號進行參數估計。

下面以單載頻信號來具體分析。

設輸入的單載頻信號為:

(2)

其頻譜為:

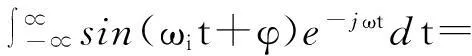
πδ(ωi-ω)e-jφ+πδ(ωi+ω)e-jφ

(3)

根據數字信號處理知識可知時域采樣會造成頻譜的周期延拓，因此，采樣后信號的頻譜Xs(ω)與采樣前信號的頻譜X(ω)關系為：

(4)

所以對信號x(t)以固定的采樣頻率Ωs采樣后的數字序列頻譜為：

(5)

由上式可知，在欠采樣的條件下，信號的準確頻率可以根據信號頻譜測得的模糊頻率值和相對于采樣頻率的模糊數目算出，即：

(6)

式中:ω和f為根據頻譜測得信號的有模糊頻率;n為模糊數目。

從上述分析可知，用欠采樣方法估計原信號的頻率是可行的，下面介紹一種常見的欠采樣解模糊方法——正交雙通道延遲解模糊。

使用正交雙通道延遲解模糊，會有4個通道，并且使用相同的采樣頻率，這種結構可以將輸入信號轉化為復信號，以保證輸入頻譜是單邊譜，因此也就不會存在雙邊譜相互之間干擾的問題，進行譜峰搜索就能定位正確的信道，得到正確的相位差，從而保證測頻的準確性[5]。目前ADC已經具有正交雙通道采樣的能力，硬件實現相對簡單。此方法的原理框圖如圖7所示。

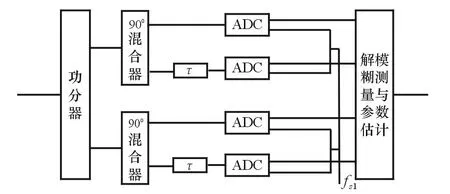
圖7　正交雙通道延遲解模糊結構

下面設定仿真參數：設被估計的信號為單載頻信號，其采樣頻率fs=170 MHz，做4 096點FFT，延時時間為τ=0.2 ns，信噪比范圍是0～60 dB，輸入信號頻率為1 GHz，在每個信噪比條件下做100次蒙特卡洛實驗，仿真得到正交雙通道延遲法測頻性能與信噪比關系，如圖8所示。

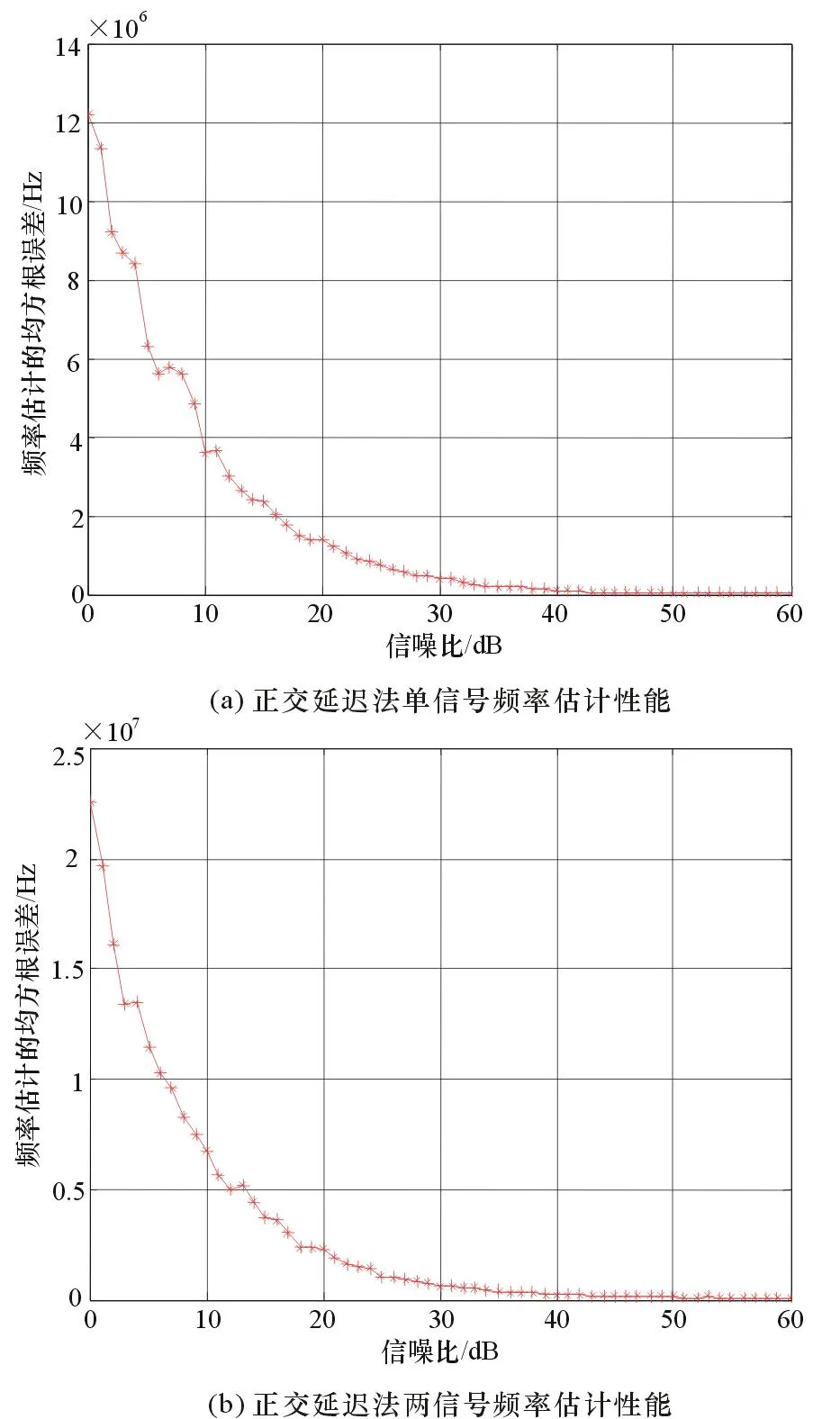
圖8　正交雙通道延遲法頻率估計性能曲線

3基于STFT的欠采樣測頻技術

在實際工程實現中，器件性能會對數字電路的速度產生很大的限制，因此，基于STFT的數字信道化技術能夠進行無模糊估計的頻率范圍也受到了很大的限制，射頻信號的頻率就很難直接進行無模糊估計。所以提出將基于STFT的數字信道化技術與欠采樣測頻技術相結合，這樣既具有信道化的優點，又能夠直接對射頻信號進行頻率估計，可以使數字接收機的模/數轉換器(ADC)盡量接近天線的模型。

正交雙通道延遲解模糊的方法是以FFT為基礎的，通過對輸入序列的FFT結果進行處理，得到相位差或者頻率的有模糊估計，經過解模糊算法得到頻率的準確估計。而基于STFT的信道化輸出結果即為函數窗內采樣序列的FFT，所以可以使用欠采樣頻率先對射頻信號數字化，然后再經STFT得到每個時間窗內輸入信號之間的相位差，進而根據相位差經過解模糊算法得到每個時間窗內信號的頻率分量，從而實現用較低的采樣頻率對射頻信號頻率進行準確估計。

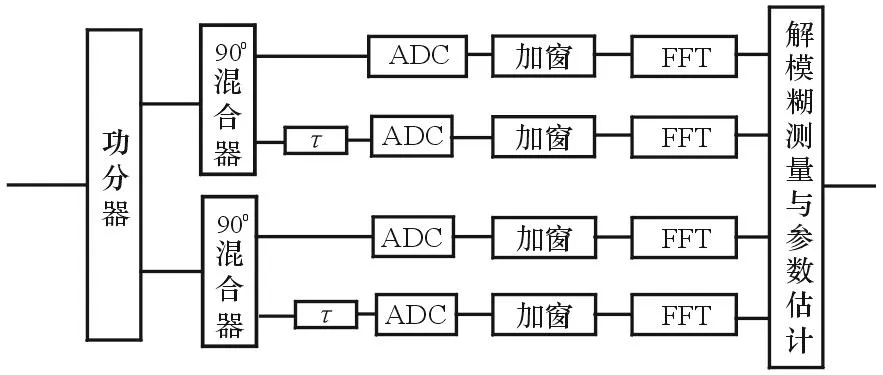
圖9　欠采樣條件下的STFT信道化結構框圖

圖9是以正交雙通道延遲解模糊為例的欠采樣STFT信道化結構框圖，這種方法就能夠用較低的采樣率實現射頻寬帶信號的頻率估計。

欠采樣條件下的STFT信道化技術實現的流程為：功分器將信號分為2路，每一路又進行正交延時，這樣就會出現4個通道，經加窗處理后根據窗寬進行補零操作，然后對窗內的數據進行FFT，根據FFT輸出的當前時刻頻譜進行譜峰搜索，得到輸入信號之間的相位差，通過解模糊算法估計出該時間窗內信號的準確頻率，同時測量信號的時域參數，窗函數滑動固定的點數，分析下一時刻的信號頻率分布，直至全部數據處理完畢，根據窗函數滑動得到的每一時刻的信號頻率分布繪制信號頻率分布與時間的關系曲線,如圖10所示。

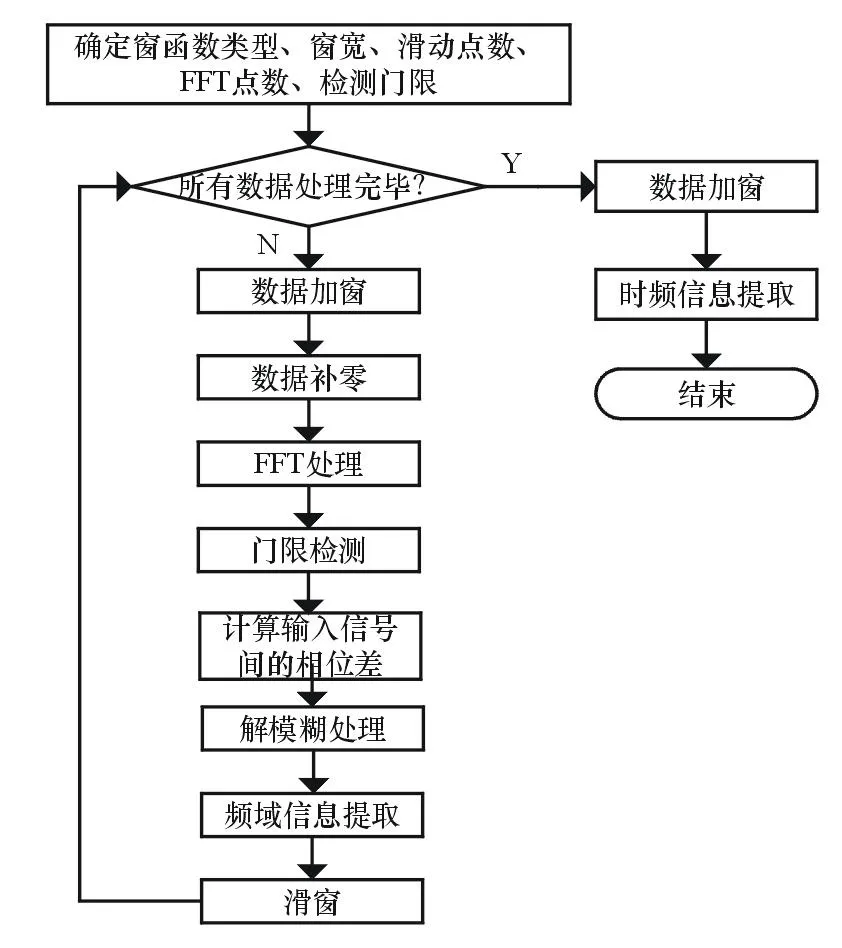
圖10　欠采樣條件下的STFT信道化流程圖

下面設定仿真參數：設采樣頻率為fs=400 MHz；輸入信號為時域完全重疊的兩信號。

對單載頻與線性調頻信號分別仿真驗證，單載頻信號參數為：f1=900 MHz，周期TPRI1=614.4 μs，脈寬TPW1=307.2 μs，幅度A1=1 V，f2=1.05 GHz，周期TPRI2=614.4 μs，脈寬TPW2=307.2 μs，幅度A2=1 V；線性調頻信號參數為：起始頻率f1′=900 MHz，帶寬B1=30 MHz，周期TPRI1=614.4 μs，脈寬TPW1=307.2 μs，幅度A1=1 V，起始頻率f2′=1.05 GHz，帶寬B2=20 MHz，周期TPRI2=614.4 μs，脈寬TPW2=307.2 μs，幅度A2=1 V。

兩通道STFT濾波器組參數設置：

通道1：STFT所用的窗函數為矩形窗，窗函數長度為1 024點，窗函數滑動點數512點，FFT點數4 096點；

通道2：STFT所用的窗函數為矩形窗，窗函數長度為1 536點，窗函數滑動點數768點，FFT點數4 096點；

STFT輸出的無模糊頻率與時間關系的時頻分析曲線如圖11所示。

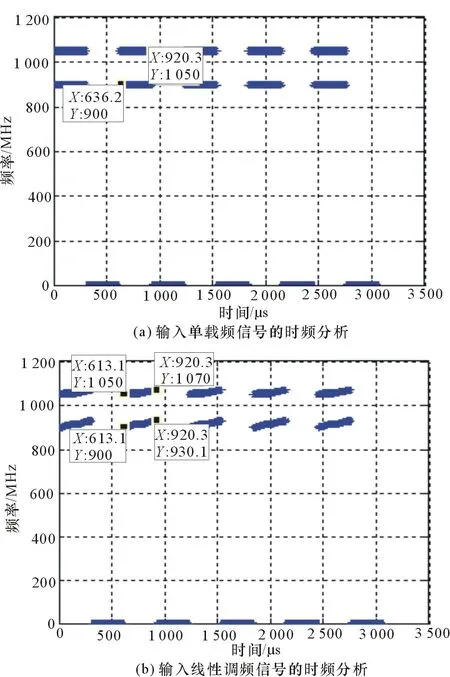
圖11　欠采樣STFT信號頻率估計的時頻分析仿真

從仿真結果可以看出，欠采樣條件下基于STFT的信道化結合解模糊算法可以有效地估計高頻信號，具備數字信道化的優點，可以分析雷達脈沖信號的時域與頻域信息，降低了采樣速率，對數據處理的速度要求降低，算法的測頻性能決定于解模糊算法的性能。

4結束語

隨著電子對抗技術的不斷進步，接收機系統在作戰中的表現也越來越受到重視，而在數字接收機的設計中，信道化技術又是舉足輕重的[6]。將典型的欠采樣解模糊算法應用于STFT數字信道化方法，兼有了欠采樣與信道化的優點，可以用較低的頻率實現對高頻信號的無模糊估計，借助信道化提高了檢測概率，增加了實時性，可以對信號參數與信號形式進行預估計。

參考文獻

[1]趙國慶.雷達對抗原理[M].西安:西安電子科技大學出版社，2005.

[2]王宏偉，趙國慶，王玉軍,等.一種寬帶數字信道化接收機[J].西安電子科技大學學報(自然科學版),2010,37(3):487-491.

[3]王開,束坤.一種基于STFT的數字信道化方法[J].艦船電子對抗,2013,36(5):56-60.

[4]黃佑勇,王激揚,陳天麒.基于欠采樣的寬頻段信號頻率估計技術[J].電波科學學報,2001,16(2):275- 279.

[5]WILLIE H M.Wideband Signal Detection Using A Down Converting Channelized Receiver[D].Ohio:Air Force Institute of Technology,2006.

[6]都佰勝．欠采樣測頻與信號處理技術[D].西安：西安電子科技大學,2009．

A Sub-sampling Frequency Measurement Technique Based on STFT

LV Hao,LUO Ming

(Xidian University，Xi'an 710071，China)

Abstract:In modern electronic warfare,the development of digital frequency measurement technique is very important.This paper performs the principle analysis and theory simulation to short time Fourier transform (STFT) digital channelization measurement technique,then studies the sub-sampling technique,and puts forward the frequency measurement method combining STFT channelization technique with sub-sampling technique,and taking orthogonal dual-channel delay ambiguity resolution as an example,validates the feasibility of the method through simulation.

Key words:frequency measurement;short time Fourier transform；digital channelized technique；sub-sampling

DOI:10.16426/j.cnki.jcdzdk.2016.01.003

中圖分類號：TN971.1

文獻標識碼：A

文章編號：CN32-1413(2016)01-0015-06

收稿日期:2015-11-03