基于改進型最大信噪比算法的抗壓制性干擾研究

王　雨

(西安電子科技大學，西安 710071)

?

基于改進型最大信噪比算法的抗壓制性干擾研究

王雨

(西安電子科技大學，西安 710071)

摘要：自雷達誕生以來，抗干擾能力一直是評價一部雷達性能的關鍵性指標，特別是隨著戰(zhàn)場電磁環(huán)境的日益復雜，雷達抗干擾問題變得尤其重要。針對抗壓制性干擾，改進了傳統(tǒng)意義上基于最大信噪比的盲源分離算法，提出了使用干擾重構算法取代滑動平均處理的方法，獲得了比傳統(tǒng)方法分離出質量更高的雷達信號，輸出信號與源信號相關性更強。

關鍵詞：抗壓制性干擾；盲源分離；最大信噪比；干擾重構

0引言

現代戰(zhàn)爭中，雷達電子對抗的作用日益凸顯，雷達抗干擾性能成為衡量一部雷達優(yōu)劣的重要指標。戰(zhàn)場上電磁環(huán)境極其復雜，敵方蓄意干擾、友方同頻波段、各種工業(yè)波段、自然環(huán)境中的各種雜波等充斥整個空間,所以研究雷達抗干擾技術是十分有意義的。目前在有源干擾方面，雷達干擾機主要使用壓制性干擾和欺騙性干擾兩大類，其中壓制性干擾主要通過發(fā)射大功率的噪聲信號來掩蓋或吞沒敵方雷達熒光屏上的目標回波信號，使敵方雷達無法正常工作[1]；壓制性干擾主要以噪聲調頻干擾為主，所以本文主要研究了基于信噪比最大化的盲源分離技術抑制噪聲調頻壓制性干擾的問題。

盲源分離技術是指在源信號和傳輸通道參數未知的情況下，根據輸入信源信號的統(tǒng)計特性，僅由觀測信號檢測并分離出信源信號中各個獨立成分的過程，這一過程又稱為獨立元分析(ICA)[2]。近年來盲源分離在語音、通信、生物電等信號處理領域的應用日益廣泛。它起源于對神經網絡的研究，在1985～1989年，法國學者Jutten和Herault考慮了2個源信號的瞬時混疊和分離問題，提出了簡單的高階去相關神經網絡方法[3]；1994年P.Comon提出了ICA的概念，并給出了相關信息論準則[4]；張賢達教授等人提出了一種新的信號盲分離算法，可以系統(tǒng)化地得到全部獨立分量[5]。以上算法都是基于自學習循環(huán)迭代得到某種目標函數最優(yōu)化的算法，2001年J V Stone提出了基于時頻預測的盲源分離算法，為最大信噪比盲源算法提供理論基礎。該種算法在預測源信號的過程中形成了廣義特征值問題[6]，該問題的特征向量就是混合矩陣的分離矩陣近似，因此該算法具有低復雜度，不需要迭代運算。但文獻[7]簡單地使用滑動平均算法對源信號進行預測，預測度并不高。本文提出了使用干擾重構算法代替滑動平均，取得了對源信號較好的估計，將此估計作為最大信噪比盲源分離算法中的信號預測，最終分離出較好的源信號。

本文首先對雷達使用的信號模型和干擾模型進行了研究；然后描述盲源分離的數學原理，對混合信號進行去中心化和白化預處理后，采用干擾重構算法得到源信號的預測，采用預測信號與預測信號和源信號之間的誤差之比作為信號最優(yōu)化的判別，求出分離矩陣，再處理分離后的信號得到目標物距離。

1信號模型

1.1雷達發(fā)射信號模型

雷達使用的發(fā)射信號種類繁多，單從信號的頻域波形方面考慮就有：跳頻信號、頻率分集信號、寬瞬時帶寬信號、脈沖壓縮信號、頻率捷變信號、波形捷變信號、相位編碼信號等。本文采用的源信號為典型的線性調頻信號，其數學表達式為：

(1)

式中:τ為脈寬;f0為中心頻率;μ為調頻斜率。

假設目標為靜止的，因此雷達回波信號僅僅包含時移τ0=2R/c，即s0(t-τ0)，其中R為目標物距離雷達的徑向距離，c為光速。

1.2壓制性干擾模型

壓制性干擾主要分為：噪聲調頻干擾、射頻噪聲干擾、噪聲調幅干擾以及噪聲調相干擾等，其中噪聲調頻干擾使用最為廣泛，所以本文中使用的干擾模型將采用噪聲調頻干擾，其數學表達式為：

(2)

式中:調制噪聲u(t)為零均值的廣義平穩(wěn)隨機過程；φ為[0,2π]均勻分布的隨機變量，且與u(t)相互獨立；噪聲調頻干擾的振幅Uj、中心頻率wj和調頻斜率KFM都為常數。

2干擾重構算法

在文獻[8]中介紹了一種干擾重構的算法，基本原理就是從回波中得到干擾參數，重構干擾信號，從雷達接收信號中消去重構的干擾信號，達到抑制干擾的作用。這里假設雷達接收信號模型為：

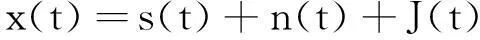
(3)

(4)

式中:s(t)為目標回波信號;n(t)為等效噪聲信號;J(t)為噪聲調頻干擾信號。

因為當干擾功率比較大時等效噪聲的干擾效果就會減弱，所以高干信比條件下，可以將等效噪聲與目標回波和記為：

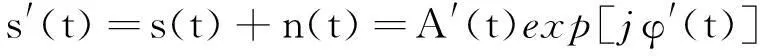
(5)

此時：

(6)

利用噪聲調頻干擾的恒模特性，可以將上式寫為：

(7)

(8)

由上式可得：

(9)

對式子兩邊同時進行對數運算，并進行一階泰勒展開得：

ln[x(t)]=ln[J(t)]+ln[1+s1(t)]≈

ln(Aj)+j[φj(t)-2kπ]+s1(t)

(10)

分別取它的實部和虛部，記為Rx(t)和Ix(t)，則有：

(11)

(12)

利用目標回波信號和噪聲調頻干擾信號是零均值的特性，可以估計干擾信號的幅度：

(13)

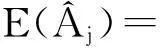
exp{E{mean{lnAj+Re[s1(t)]}}}=

exp{lnAj+E{mean{Re[s1(t)]}}}=Aj

(14)

進而可以得到：

(15)

在|s1(t)|?1的條件下，干擾信號的估計為：

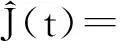
(16)

從接收信號x(t)中消去干擾信號的估計值可以得到目標回波信號的估計：

(17)

這樣就可以得到雷達目標回波信號，該算法的缺點是對干信比比較敏感，即大功率干擾下目標回波估計較差，因此單獨作為干擾抑制算法效果很差，但作為從雷達接收信號中估測源信號，不僅估測精度比滑動平均處理好而且運算量小，之后通過最大信噪比盲源分離算法處理后，使得分離效果更好。下面介紹最大信噪比盲源分離算法模型。

3改進型最大信噪比的盲源分離抑制干擾算法

盲源分離是在對原始信號的特征了解甚少，甚至不知道混合信號中源信號數目的情況下，從混合信號中分離出原始信號[9]。由于只能得到雷達天線的接收信號以及發(fā)射信號副本，且接收信號中包含了大量的干擾成分，所以可以假設如下信號模型：

(18)

式中：x(t)為雷達觀測信號矩陣，x(t)=[x1,x2,…,xn]T;s0(t)為純凈的雷達回波信號和單純的干擾信號構成的矩陣;A為干擾強度、雷達天線、系統(tǒng)噪聲等因素決定的混合矩陣。

假設分離矩陣為W，則對源信號的估計信號y(t)為：

y(t)=Wx(t)=WAs0(t)

(19)

在此信號模型中，將抽取源信號和其估計信號的誤差：e=s0-y，只要使該誤差最小化，則可以將信號y(t)作為源信號s0(t)的估計，進而分離出雷達回波信號，抑制干擾。文獻[7]給出了信噪比函數作為誤差最小化的計算公式：

(20)

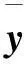
(21)

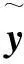
(22)

以F(y)作為目標函數進行自學習，使得輸出信號與源信號的誤差最小，得到較好的源信號估計。進一步可對目標函數進行如下運算：

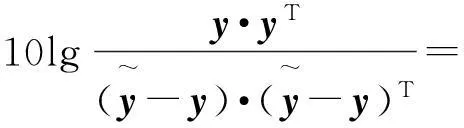
(23)

進而求其關于分離矩陣W的梯度：

(24)

因為在最大信噪比的極值點處該梯度值等于0，于是可以得到：

(25)

4仿真實驗與結果分析

為了驗證上述理論，設定如下仿真參數：雷達發(fā)射信號的脈沖周期T=40 μs，信號帶寬B=30 MHz，信號采樣率Fs=100 MHz，接收窗口[10 000,15 000]m,目標物與雷達徑向距離R=12 000 m。干擾信號為噪聲調頻信號，調頻斜率Kfm=1 000，中心頻率f0=15 MHz，干擾帶寬=20 MHz，采樣點數為4 000，信噪比=10 dB，干信比=30 dB；干擾信號時頻圖如圖1所示，雷達接收機接收到的兩路信號如圖2所示。

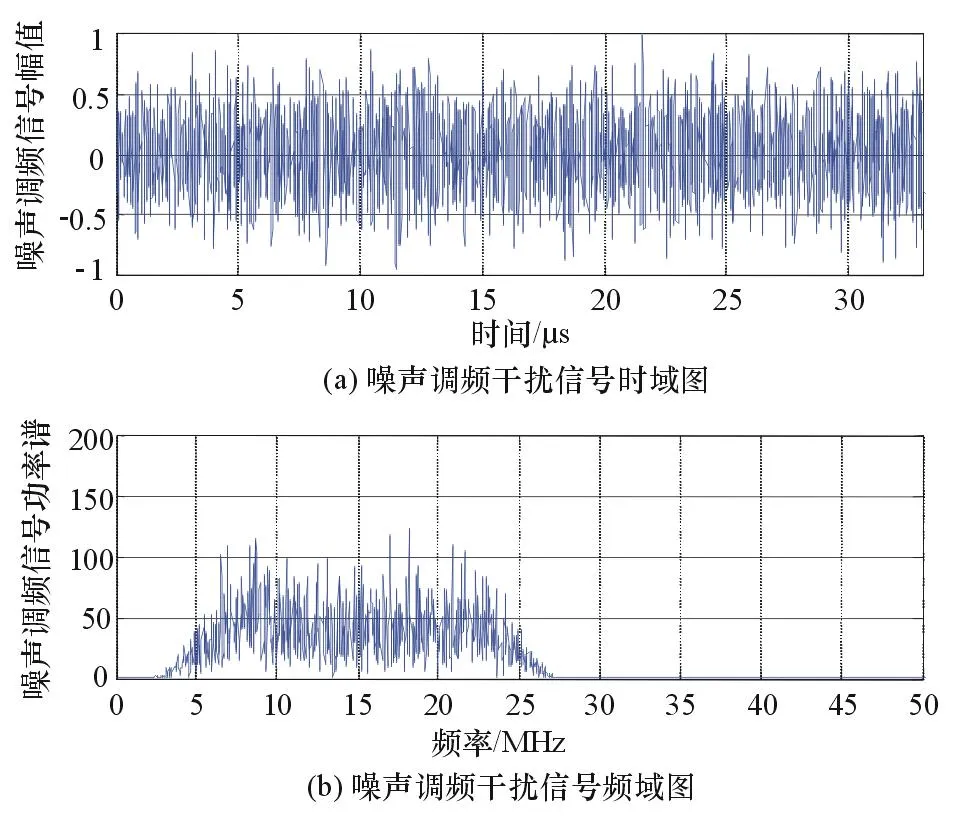
圖1　干擾信號時頻圖

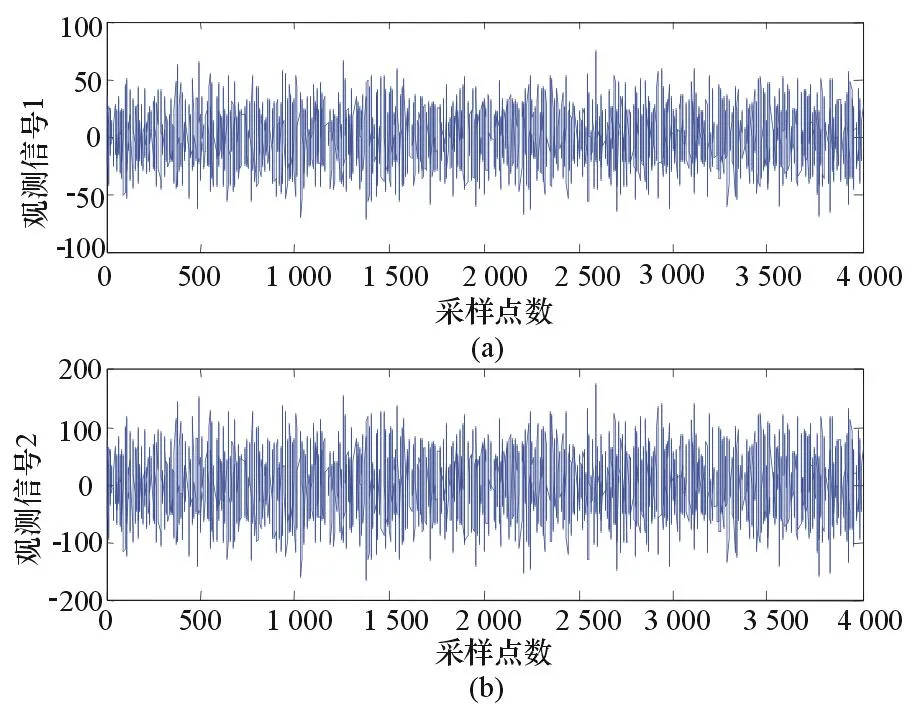
圖2　雷達接收機觀測信號

在含有噪聲以及高功率干擾條件下，目標回波波形失真嚴重，如不采用相關抑制算法將得到如圖3所示的處理效果圖，無法得到目標參數。圖4將采用傳統(tǒng)的基于最大信噪比盲源分離算法進行干擾抑制處理。

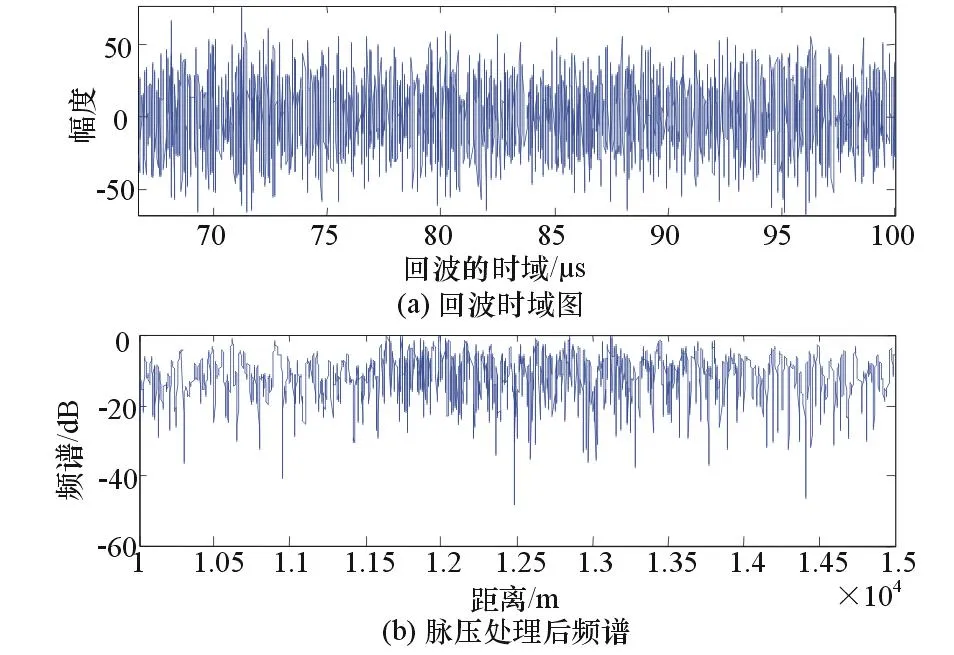
圖3　傳統(tǒng)算法抑制效果圖4最大信噪比盲源分離效果

圖4是30dB干信比下，雷達接收機接收到的信號經過最大信噪比盲源分離算法后分離出的2路信號:一路是干擾信號，另一路是目標回波信號，發(fā)現經過分離之后的有用信號波形接近時移后的雷達發(fā)射波形，為了證明該信號就是目標回波信號，接著進行了脈壓處理得到圖5。

圖4　最大信噪比盲源分離效果

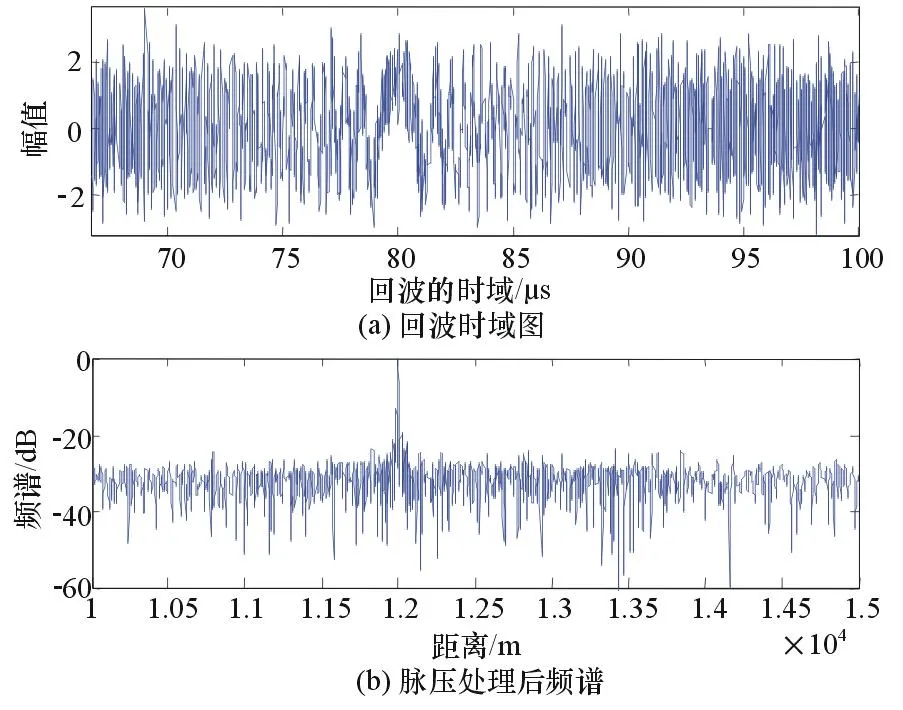
圖5　最大信噪比分離后脈壓效果

圖5是傳統(tǒng)的最大信噪比盲源分離算法分離出的結果，噪聲起伏較大。圖6是經過了改進的基于干擾重構的最大信噪比盲源分離算法，對比圖5可以發(fā)現波形質量較高，為了定量地比較兩算法優(yōu)劣，引入了相關系數作為參數，比較兩者分離出的信號與雷達發(fā)射信號的相關程度，仿真如圖7所示。

圖6　改進后的分離算法脈壓效果

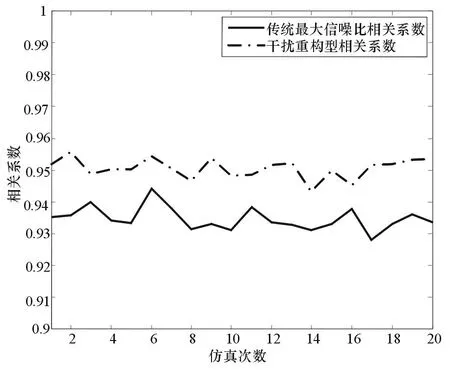
圖7　算法改進前后相關系數對比

從仿真結果可以得出：基于最大信噪比的盲源分離算法能很好地探測目標物距離為12 000m。但使用干擾重構的最大信噪比分離算法分離出的信號與源信號相關度更大，即分離效果更好；在運算復雜度方面，兩者處于同一量級，改進型算法并沒有增大運算量。

5結束語

本文提出的使用干擾重構作為最大信噪比盲源分離算法中的源信號估測的方法，使得信號預測比單純的滑動平均處理效果更好，進而后續(xù)分離出的信號質量也更高，與源信號的相似度更大。但本文只選取了噪聲調頻干擾信號，對其他壓制式干擾抑制效果較差，這時可以使用最小均方差(LMS)濾波算法代替滑動平均，能得到相似的結果。

參考文獻

[1]趙國慶.雷達對抗原理[M].2版.西安：西安電子科技大學出版社，2012：122-151.

[2]HYVARINENA.獨立成分分析[M].周宗潭,董國華,徐昕,等譯.北京：電子工業(yè)出版社，2014:142- 178.

[3]COMONP.Separationofstochasticprocess[C]//WorkshoponHighorderSpectrumAnalysis.Colorado,1989:174-179.

[4]馮大政.保錚.張賢達.信號盲分離問題多階段分解算法[J].自然科學進展，2002，12(3)：324-328.

[5]HERAULTJ,JUTTENC.Spaceortimeadaptivesignalprocessingbyneuralnetworkmodel[C]//AmericanInsitituteforPhysics:NeuralNetworksforComputingAIPconfProceeding151.NewYork:AmericanInsitituteforPhysics,1986:13-16.

[6]STONEJV.Blindsourceseparationusingtemporalpredictability[J].NeuralComputation，2001(7):150- 165.

[7]張小兵.馬建倉.陳翠華.劉恒.基于最大信噪比的盲源分離算法.計算機仿真,2006(10):72-75.

[8]杜東平.雷達壓制式干擾抑制算法研究[D].成都:電子科技大學,2008:78-83.

[9]黃高明.盲信號處理及其在無源探測中的應用研究[D].南京：東南大學,2005:1-8.

[10]BORGAM.LearningMultidimensionalSignalProcessing[D].Linkoping,Sweden:LinkopingUniversity,1998.

Research into Anti-blanket Jamming Technology Based on Improved Maximum SNR Algorithm

WANG Yu

(Xidian University，Xi'an 710071,China)

Abstract:Since there are radars,anti-jamming capability is always the key index to evaluate a radar,especially with the increasing complication of battlefield electromagnetic environment,anti-jamming problem of radar becomes particularly important.For anti-blanket jamming,this paper improves the blind source separation algorithm based on traditional maximum signal to noise ratio,presents the method that uses jamming remodelment algorithm to replace the slide average treatment method, then gets the radar signal of better quality than by traditional method,and the correlation between the output signal and the source signal is stronger.

Key words:anti-blanket jamming;blind source separation；maximum signal to noise ratio；jamming remodelment

DOI:10.16426/j.cnki.jcdzdk.2016.01.006

中圖分類號：TN974

文獻標識碼：A

文章編號：CN32-1413(2016)01-0031-05

收稿日期:2015-11-03