基于ANSYS的石油井架整體穩定性分析

盛　尹， 熊　峰， 葛　琪

(四川大學建筑與環境學院， 四川成都 610065)

?

基于ANSYS的石油井架整體穩定性分析

盛尹， 熊峰， 葛琪

(四川大學建筑與環境學院， 四川成都 610065)

【摘要】基于ANSYS對井架進行了線性屈曲分析和非線性屈曲分析，評估NDC-50DBT型石油鉆機井架的整體穩定安全性能。論文提出屈曲控制荷載和非線性折減系數的概念，考慮幾何和材料雙重非線性，引入結構初始缺陷，采用弧長法進行非線性屈曲全過程跟蹤。結果表明：對井架結構進行整體穩定分析時，有必要考慮風荷載的影響；相對于線性屈曲分析，非線性屈曲分析的屈曲因子為線性屈曲因子的0.33～0.72倍；考慮幾何和材料雙重非線性的多工況分析，能夠更全面真實的反應井架穩定極限承載能力，為井架的設計和使用提供參考。

【關鍵詞】井架；穩定性；非線性；有限元

石油鉆機井架是鉆機系統起升設備的重要組成部分，是用于放置天車和懸掛游車、大鉤的專用工具，其性能直接關系到整套鉆機系統的安全運行[1]。石油工程中使用的各種鉆機井架大部分是由細長桿組成的桿系塔桅結構，使用中容易失穩。而鉆井工程中發生的井架毀壞事故，往往是由于井架失穩造成的[2]。因此，對井架結構進行整體穩定性分析具有重要的實際意義。

本課題組基于ANSYS軟件分析平臺，對井架的整體穩定性進行評估，指導NDC-50DBT型石油鉆機井架的設計和優化。為準確評價石油井架安全性能，本論文提出了井架屈曲控制荷載和非線性折減系數的概念，結合美國石油協會API規范和安裝使用的實際，分析井架可能存在的危險工況，對各工況進行線性屈曲分析，得到結構線性屈曲因子。在此基礎上，考慮結構初始缺陷，以線性屈曲模態修正有限元模型，考慮材料、幾何雙重非線性，對各工況進行非線性屈曲分析，求得非線性屈曲因子，全面評價井架力學性能，指導井架結構的優化改進。

1整體穩定性分析基本原理和方法

結構失穩是指結構在外力作用下平衡狀態開始喪失，稍有擾動則變形迅速增大，最終遭到破壞的過程。對于石油鉆機井架，就其性質而言，其失穩形式可分為線性屈曲和非線性屈曲[4]。

1.1線性屈曲分析原理

線性屈曲又稱分支點失穩或第一類失穩。線性屈曲分析在數學上其可歸結為廣義特征值問題。對于線彈性構件，荷載-位移關系的矩陣形式為[5]：

(1)

式中：[P0]為施加荷載；[K]為剛度矩陣；[u0]為施加荷載[P0]的位移結果。

因此，增量的平衡方程為：

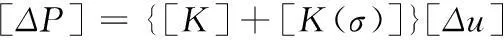
(2)

式中：[K(σ)]為應力狀態[σ]下計算的剛度矩陣；[σ]為與[u0]對應的應力。

假設這是一個線彈性行為，則有：

得：

(3)

式中：μ為特征值。

當構件發生屈曲時 [ΔP]=0，則有：

(4)

由式(4)可以求得特征值μ，進而得到結構的臨界屈曲荷載Pcr。

盡管線性屈曲只能用于預測理想線彈性結構的理論屈曲強度，對實際井架結構分析只能得到非保守結果，但是該方法計算速度快，有利于初步了解結構的穩定性，分析得到的臨界荷載可作為后續非線性屈曲分析的目標荷載，屈曲模態也可作為非線性分析中引入初始缺陷的依據[6]，因此在進行整體非線性屈曲分析前，有必要對井架結構進行線性屈曲分析。

基于ANSYS的Eigen Buckling分析模塊，可計算得到井架結構一系列的線性屈曲特征值。其中的最小值μ即為通常所稱的線性屈曲因子或線性屈曲安全系數。結構的臨界荷載為：

(5)

式中：Pcr為臨界荷載；P為施加荷載。

然而，在安裝使用過程中，并非所有荷載都對井架結構的屈曲起控制作用(如井架體自重)。把作用在井架上的荷載分為屈曲控制荷載和不變荷載，則式(5)可改寫為：

(6)

式中:P1為控制荷載;P2為不變荷載。

由式(6)可以看出，將此處的μ作為井架結構的屈曲因子進行穩定性安全評價并不準確。

本課題組在對井架進行線性屈曲分析計算中，通過命令流不斷調整式(6)中的控制荷載P1，使得到的結構最小特征值μ=1，此時式(6)可改寫為：

(7)

(8)

將式(8)中的α作為井架的線性屈曲因子，這樣能更準確反映井架的線性屈曲安全性能。PX稱為施加的目標荷載。

1.2非線性屈曲分析原理

非線性屈曲又稱極值點失穩或第二類失穩。非線性屈曲分析屬于全過程大撓度彈塑性有限元方法，通過逐級增加荷載，不斷修正單元的剛度矩陣，對結構進行非線性靜力學分析，在此基礎上尋找結構變得不穩定時的臨界荷載。該方法能同時考慮結構的幾何非線性、材料非線性以及結構初始缺陷。

借助ANSYS中的弧長法能實現石油井架非線性仿真分析?；￠L法是一種穩定可靠的迭代控制方法，能有效的對平衡路徑全過程跟蹤。

在非線性屈曲分析時，本課題組結合改進的線性屈曲分析方法所得到的結果，采用多荷載步增量加載的方式，在0～10-6s時間步長內完成式(7)中不變荷載P2的等量逐步加載，接著在10-6～1 s內對目標荷載PX進行等量逐步加載，直到求解發散，非線性分析停止，得到分析停止時間T。

在分析計算中，ANSYS荷載步中的任意子步將被賦予合適的、線性插值得到的時間值，所以時間就可以作為荷載施加的跟蹤參數[7]。井架結構的非線性屈曲因子(非線性屈曲安全系數)按式(9)計算。

(9)

式中：n為非線性屈曲因子；α為相應工況線性屈曲因子；T為ANSYS非線性分析終止時間，可視為非線性折減系數。

該分析過程中考慮結構的幾何非線性和材料非線性，同時參考文獻[6]中對空間鋼結構的分析方法，以結構一階線性屈曲模態位移值的0.1倍修改原模型節點坐標，作為結構的初始缺陷。

2荷載與工況分析

2.1井架的計算荷載

作用在井架上的荷載可分為恒定荷載、工作荷載和自然荷載，在進行井架結構整體穩定性分析時，考慮如下荷載：

(1)恒載。包括井架體本身的重量以及安放在井架上面的各種附件設備(主要包括井架自重、二層臺重量、天車重量、游動系統等)的重量。

(2)最大鉤載。即鉆機最大起重量,是鉆機的一個主參數。

(3)工作繩作用力。在給定的游動系統下，快繩和死繩拉力的垂直分力。

(4)立根荷載。在鉆井過程中靠放在鉆臺上的立根對井架產生的作用力，通過二層臺指梁按水平方向作用到井架。

(5)風載。井架結構在環境風作用下所受到的荷載，包括井架體風載和立根風載。

2.2荷載工況

結合API規范和實際安裝使用情況，考慮井架生命周期可能出現的平躺、起升、豎直狀態，整體穩定性計算工況見表1。

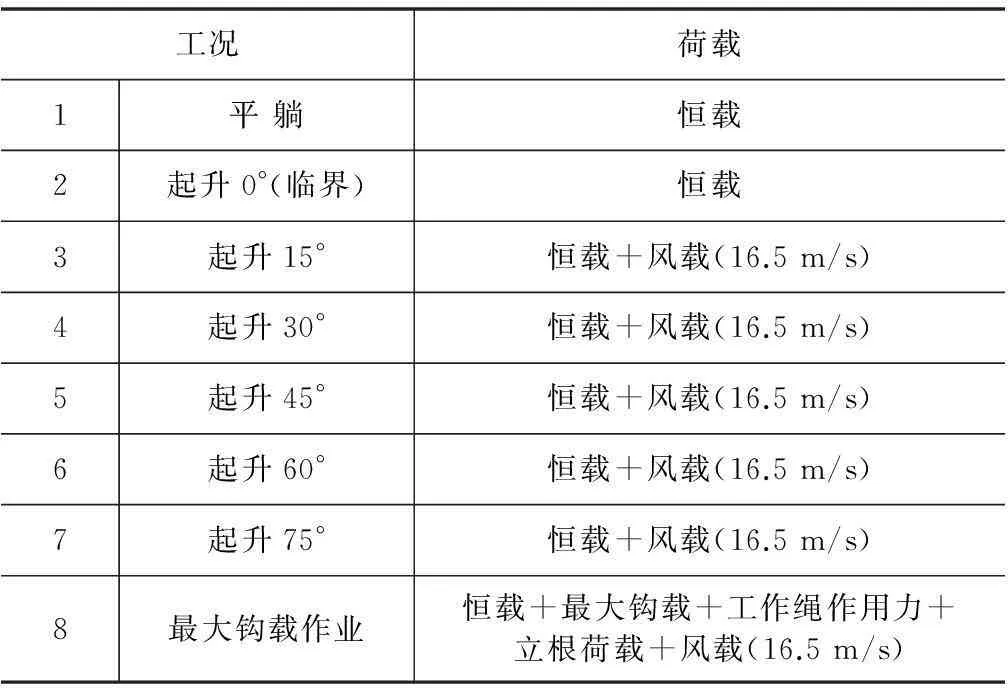
表1　荷載工況

注：①對于計入風載的工況，分別考慮X、Y風向；

②井架安裝作業設計抗風能力為16.5 m/s。

3有限元分析模型

3.1模型建立

該井架為前開口型結構，屬6×7輪系，最大設計鉤載4 500 kN，由上、中、下段組成。在ANSYS中建立模型時，作如下假設簡化：井架桿件間連接可靠，為剛性連接；忽略二層臺、天車、工作梯及護欄等對井架的剛度影響，只計入其自重荷載。分別建立各狀態結構模型，其中井架豎直狀態模型如圖1所示。

圖1　結構模型(豎直狀態)

結構構件采用Q345和Q420鋼材，材料參數如表2所示。考慮材料非線性時，選用雙線性等向強化模型，即材料應力-應變曲線由兩段直線組成，包括彈性和塑性兩個斜率。彈性段斜率為彈性模量E，塑性段斜率ET取值為0.1E。

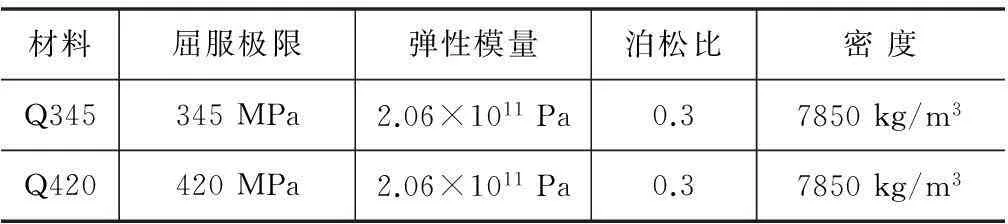
表2　材料參數

選用BEAM189單元進行模擬分析。BEAM189是3D二次有限應變梁單元，非常適用于線性、大角度轉動和非線性大應變問題。設置單元屬性 KEYOPT(1)=1，添加單元第7個自由度(橫截面的翹曲)。綜合考慮分析精度和時間內存消耗，模型單元長度設為0.2 m，共4 080個單元，11 396個節點。

3.2荷載施加

對表1中各工況按以下方式分別施加荷載：

(1)井架體自重以慣性力的方式施加。

(2)二層臺相關附件重量均分到二層臺架體各節點上。

(3)游車、鉆井繩及其他附件的重量均分到井架頂端4個節點上。

(4)鉤載、工作繩作用力均分到井架頂端4個節點上。

(5)立根水平靠力均分到二層臺指梁相應節點上。

(6)風載分配到井架體迎風面節點上。

4結果與分析

4.1線性屈曲

以最大鉤載y風向工況為例，選取最大鉤載(P1=4 500 kN)作為結構屈曲控制荷載，其余荷載為不變荷載。當施加荷載為(6×控制荷載+不變荷載)時，結構最小特征值為1.003，接近1.0，根據式(7)、式(8)可得結構該工況線性屈曲因子α=6。結構一階屈曲模態如圖2所示。

圖2　一階屈曲模態(放大5 000倍)

同理，對其余工況進行分析，各工況控制荷載P1和線性屈曲因子α如表3所示(括號內為y風向時的結果)。

由表3可得：

(1)各工況線性屈曲因子并不相同，同種工況不同方向風荷載下屈曲因子也不完全相同，因此有必要對井架的安裝起升狀態進行分析，并考慮風荷載的影響。

(2)井架在各工況中最小線性屈曲因子αmin=6，可初步判定井架整體穩定性良好。

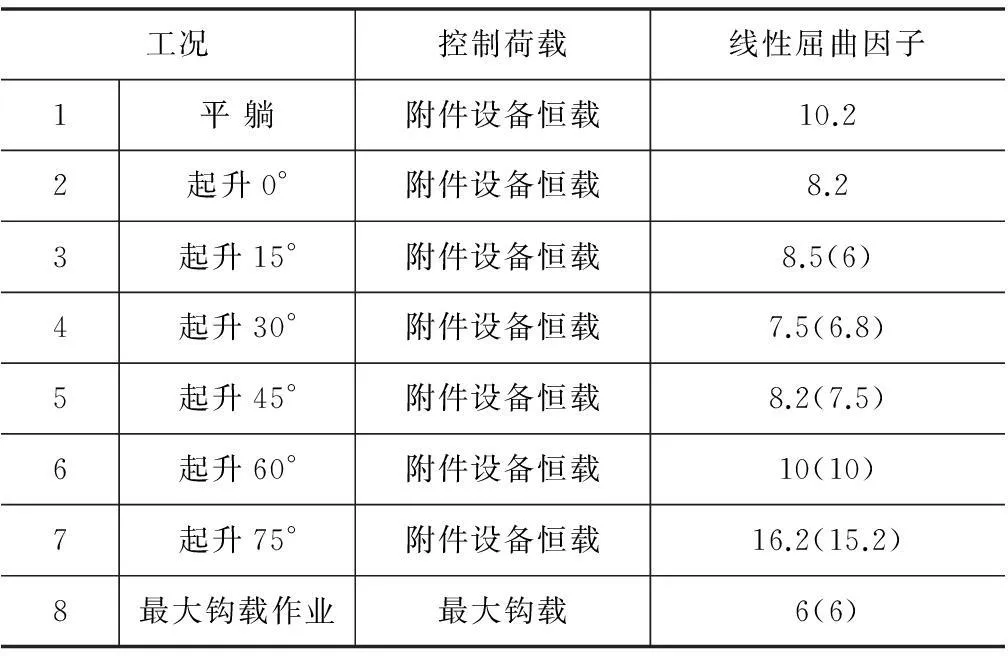
表3　各工況線性屈曲因子

注：附件設備恒載指井架結構除井架體自重外的其他所有恒載。

4.2非線性屈曲

以最大鉤載y風向工況為例，根據線性屈曲分析結果，對結構依次等量逐級施加不變荷載P2和目標荷載PX=(6×P1),得到結構非線性折減系數(分析終止時間)T=0.37，由式(9)可得井架非線性屈曲因子n=6×0.37=2.22。

圖3為該工況井架頂部節點豎向位移與荷載關系曲線。A點表示結構僅在不變荷載P2作用下頂點豎向位移值。經分析發現，當目標荷載PX達到7 110 kN(1.58倍控制荷載)附近時，井架部分構件開始進入屈服，如圖中B點所示。當目標荷載PX達到9 990 kN(2.22倍控制荷載)后，位移值迅速增加，且荷載有減小的趨勢，整體結構達到承載極限狀態，如圖中CD段所示。圖中AB段實線與虛線的偏離表明整體結構在材料屈服前因幾何非線性效應已表現出明顯的非線性現象。

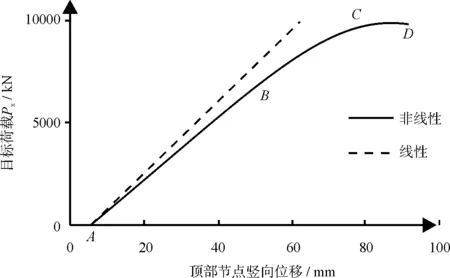
圖3　荷載位移曲線

同理，對其余荷載工況進行非線性屈曲分析，各工況非線性折減系數T及屈曲因子n如表4所示(括號內表示y風向時的結果)。

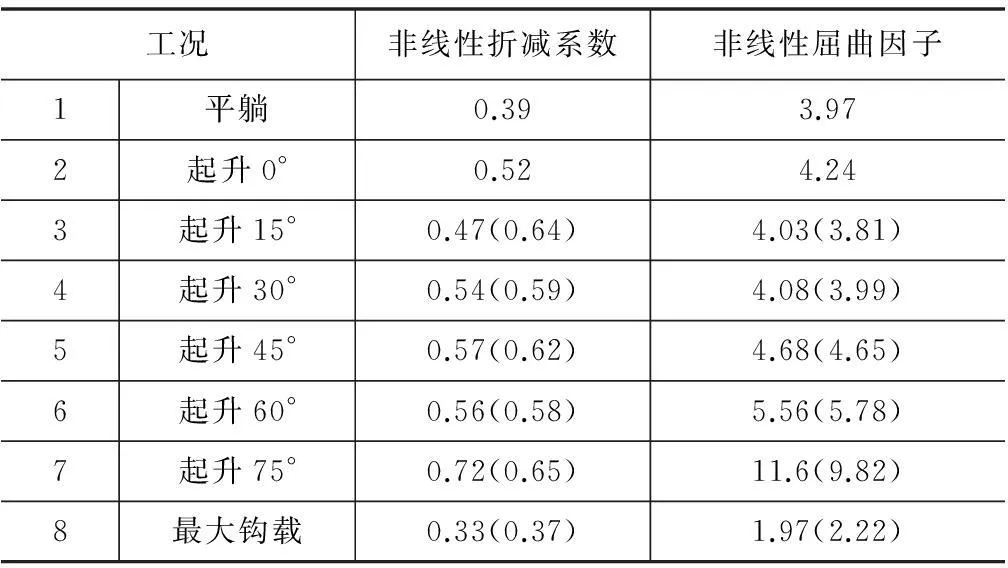
表4　各工況非線性屈曲因子

從表4可以看出：

(1)各工況非線性屈曲因子均明顯小于表3中的線性屈曲因子，其值約為線性屈曲因子的0.33～0.72倍。

(2)同種工況不同風向分析結果并不相同，表明在在非線性分析中，風荷載的影響并不能忽略。

(3)井架最小非線性屈曲因子nmin出現在最大鉤載x風向工況，大小為1.97。

5結論

通過計算分析可得出以下結論:

(1)線性分析方法會過高地估計結構的極限承載力，要準確評估出作業井架的極限承載力必須同時考慮幾何和材料非線性。

(2)相比于線性屈曲因子，非線性屈曲因子折減系數為0.33～0.72。

(3)對井架結構穩定性的安全評估，應考慮風載的作用。

(4)通常情況下，當結構的屈曲因子大于1時，可認為結構是穩定的。文獻[2]和文獻[8]中提到，井架結構的整體穩定性許用安全系數為2.2，即當屈曲因子大于2.2時井架具有足夠的整體穩定性安全裕度和良好的抗失穩性能。在所有工況非線性分析結果中，平躺起升過程的非線性屈曲因子均大于2.2，表明這些工況下結構穩定性是足夠安全的；對于最大鉤載的極限狀況，y方向風荷載時，非線性屈曲因子為2.22，能夠滿足穩定需求；對于最大鉤載x風向時，結構非線性屈曲因子為1.97，大于1，但小于文獻中的2.2，即在該極限工況下，其整體穩定性并不能得到足夠的保證，應對該結構構件的截面尺寸進行改進設計。

(5)考慮幾何和材料雙重非線性的多工況分析，能夠更全面真實的反應井架穩定極限承載能力，為井架的設計和使用提供參考。

參考文獻

[1]熊敏.考慮半剛性節點的塔形井架結構有限元分析[D].大慶:東北石油大學,2013.

[2]張學鴻,劉巨保,王惠德.3 200 m鉆機前開口井架整體穩定性分析[J].石油機械,1990,18(5):1-3.

[3]周傳喜,郭偉,南利華.海洋修井機井架穩定性計算研究[J].石油機械,2009,37(8):48-50.

[4]張嗣偉.井架總體穩定性的概念與計算原理[J].石油機械, 1978(4):117-132.

[5]高超,郭建生.圓管鋼結構穩定性的有限元分析[J].武漢理工大學學報:信息與管理工程版, 2011,33(3):421-423.

[6]陳志華,劉紅波,周婷,等.空間鋼結鉤APDL參數化計算與分析[M].北京: 中國水利水電出版社,2009.

[7]李兵,宮鵬涵.ANSYS14有限元分析自學手冊[M].北京:人民郵電出版社,2013.

[8]蔣薇,易先中,胡德祥.JJ225/42-KC型石油鉆機井架結構強度分析[J].石油機械, 2012,40(2):22-25.

【文獻標志碼】A

【中圖分類號】TE923; TU311.2

[通訊作者]熊峰(1963～)，女，教授，博士生導師。

[作者簡介]盛尹(1992～)，男，在讀研究生，研究方向：工程結構分析。

[收稿日期]2015-10-22