非凸混合總變分圖像盲復原

劉巧紅,李 斌,林 敏

(1.上海大學機電工程與自動化學院,上海 200073; 2.上海醫(yī)療器械高等專科學校醫(yī)學電子與信息工程系,上海 200093)

?

非凸混合總變分圖像盲復原

劉巧紅1,李 斌1,林 敏2

(1.上海大學機電工程與自動化學院,上海 200073; 2.上海醫(yī)療器械高等專科學校醫(yī)學電子與信息工程系,上海 200093)

摘要:為實現(xiàn)模糊噪聲圖像的盲復原,提出了一種混合非凸總變分和高階總變分的多正則化約束的圖像盲復原方法.首先,根據(jù)自然圖像邊緣的稀疏特性,運用了非凸總變分對復原圖像進行正則化約束;然后,結合高階總變分正則化克服階梯效應的優(yōu)勢,建立了非凸混合總變分極小化模型;最后,利用增廣拉格朗日方法和新的廣義p收縮算子對提出的模型進行最優(yōu)化求解.實驗結果表明,提出的方法能夠有效保護圖像邊緣細節(jié),同時消除了圖像平滑區(qū)域的階梯效應,獲得高質(zhì)量的復原圖像.

關鍵詞:圖像復原;非凸;高階;總變分;增廣拉格朗日方法;p收縮算子;優(yōu)化

圖像在采集的過程中,由于成像設備與物體之間的相對運動、對焦不準確或者大氣湍流等各種因素,極易變得模糊.模糊的圖像不僅降低了自身質(zhì)量,也會影響到圖像的后續(xù)處理及應用.圖像模糊的過程在數(shù)學上可模型化為清晰圖像卷積模糊核,并疊加噪聲,即f=u*h+n,其中,*表示卷積算子,f表示觀測的模糊圖像,u表示原始的清晰圖像,h表示模糊核函數(shù),或稱為點擴散函數(shù)(Point Spread Function,PSF),n表示噪聲.圖像復原是圖像模糊的逆過程,根據(jù)PSF是否已知,可分為圖像盲復原和圖像非盲復原兩大類.圖像盲復原是在PSF未知或已知信息量很少的情況下,對模糊圖像進行恢復.很明顯,在實際應用中,通常需要處理的是圖像盲復原問題,文中的重點即模糊圖像的盲復原.

總的來說,圖像盲復原是一個病態(tài)的反問題,通常在求解中,利用已知的先驗知識施加適當?shù)募s束,將原始的病態(tài)問題轉換為良性問題,從而穩(wěn)定原始問題的解,正則化方法是解決此類問題的有效途徑之一.總變分[1](Total Variation,TV)模型最早由Rudin等針對圖像去噪問題而提出,由于其具有強大的圖像邊緣保護能力,成為圖像去噪算法中最成功的方法之一.文獻[2]首先將TV模型作為正則項應用到了模糊圖像盲復原,很好保護了復原圖像的邊緣.然而TV正則化易于在圖像的平滑區(qū)域支持分片常數(shù)的解,會出現(xiàn)階梯效應.將高階偏導引入能量變分模型是其中一種戰(zhàn)勝階梯效應的有效方法,如四階偏微分方程模型、高階偏微分方程LLT(Lysaker-Lundervold-Tai,LLT)模型、總廣義變分(Total Generalized Variation,TGV)模型等.高階的擴散能夠更好地近似圖像平滑區(qū)域的變化規(guī)律,消除分片常數(shù)現(xiàn)象,從而抑制階梯效應.然而正是由于高階模型復原圖像時趨向于光滑,導致圖像的邊緣易出現(xiàn)模糊.

面對高階模型在圖像復原時在邊緣保持上遇到的困難,結合低階模型和高階偏導模型的圖像復原方法被提出,組合的模型能充分利用單一模型各自的優(yōu)勢進行圖像復原,從而獲得更優(yōu)的復原效果.最早的組合模型是由文獻[3]提出的inf-convolution模型,該模型結合了TV約束圖像的分片常量部分和TV的導數(shù)約束分片平滑區(qū)域構成的兩個凸正則項,來解決圖像的去噪問題.文獻[4]將TV模型和LLT模型凸組合,交替地進行求解模型,有效保持邊緣和恢復平滑區(qū)域.文獻[5]在TV模型上增加了一個非平滑的二階正則項,構造了TV和TV導數(shù)合并的凸函數(shù).該模型不僅在避免階梯效應和邊緣保持上極具競爭性,并且能方便簡單有效地進行數(shù)值求解.組合模型解決圖像復原問題,受到持續(xù)增長的關注.

相對于上述的凸變分模型,根據(jù)統(tǒng)計分析得出自然圖像的梯度符合“尖峰重尾”的分布[6],這種統(tǒng)計特性為圖像的復原問題提供了非常有用的先驗知識.文獻[6]指出,超拉普拉斯分布可更好地擬合自然圖像的“尖峰重尾”分布特征,并給出了相應的非凸圖像非盲復原的快速算法.文獻[7]就歸納了多種非凸正則項的基礎上,指出非凸正則項在保持圖像的邊緣性上優(yōu)于凸正則項.近來的許多研究也表明,非凸正則項在恢復高質(zhì)量的圖像上提供了更多的可能性[8],尤其是在邊緣和形狀的保持上.而非凸的模型在數(shù)值上求解具有一定的困難性,通常非凸問題利用lp擬范式替代凸問題中的l1范式,其中,0＜p＜1.文獻[6]在解決非凸圖像非盲復原問題時,只是給出了p取幾種特殊值的解析解,不夠明確.而近來文獻[9]設計的廣義p收縮算子,給出了非凸問題的統(tǒng)一求解模型,能方便有效地解決此類問題.

受到組合模型及非凸正則化模型優(yōu)勢的啟發(fā),為更好地實現(xiàn)模糊圖像的盲復原,筆者提出了一種結合非凸TV模型和高階擴散模型的混合總變分圖像盲復原方法.針對混合變分模型的求解,提出一種結合增廣拉格朗日方法和廣義p收縮算子的求解方法,對相應的代價函數(shù)進行最優(yōu)化的求解.

1 非凸混合變分正則化的圖像盲復原方法

1.1 非凸混合正則化模型的建立

針對圖像復原問題,非凸正則化模型具有優(yōu)于凸正則模型的邊緣保持性,高階模型的擴散能力可有效避免階梯效應和假邊緣瑕疵,組合模型綜合單一模型各自的優(yōu)勢,從而獲得更好的復原效果.在此分析的基礎上,文中分別針對自然圖像的邊緣細節(jié)和平滑區(qū)域的不同特性,提出了一種非凸總變分和高階擴散模型的混合總變分圖像盲復原模型,可表示為

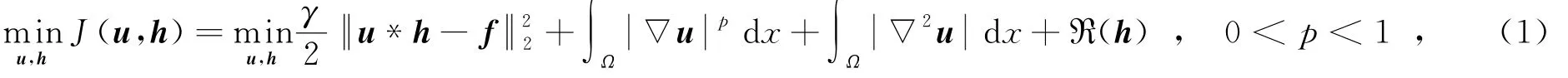
其中,?u=(Dxu,Dyu)和?2u=(Dxxu,Dyyu,Dxyu,Dyxu),分別是一階和二階偏導算子的離散形式.將圖像正則化約束項分別定義為

式(1)中,R(h)是模糊核函數(shù)的正則化約束,由于模糊核通常表現(xiàn)出明顯的稀疏性和非負性,因而采用其自身的l1范式進行約束,并且滿足:

1.2 結合增廣拉格朗日和廣義p收縮算子的交替極小化算法

式(1)中的多個約束項由式(2)～式(4)定義后,可寫為如下的優(yōu)化問題形式:

為有效計算出原始圖像u和模糊核函數(shù)h,采用了交替最小化的策略,將非約束的優(yōu)化問題式(5)轉換成關于u和h的兩個子問題交替求解.

1.2.1 原始圖像u的求解

求解u時,固定h不變,正則項為非凸TV項和高階偏導項,可得到

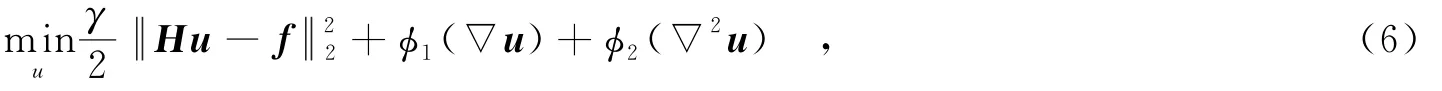
其中,H是模糊核函數(shù)h的矩陣表示,其值是由前次的迭代計算中估計得出.針對式(6),根據(jù)變量分裂準則,首先引入多個輔助變量ν=(νx,νy),ω=(ωxx,ωyy,ωxy,ωyx),式(6)被轉化為約束的優(yōu)化問題:

針對式(7)的每個約束,增加二次懲罰項,得到對應的增廣拉格朗日目標函數(shù)

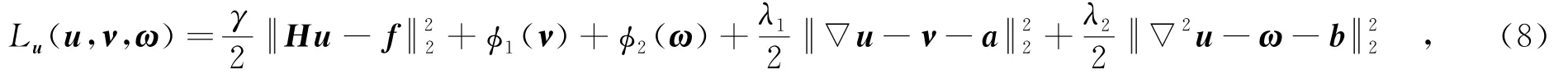
其中,a=(ax,ay),b=(bxx,byy,bxy,byx),是擴展拉格朗日乘子,λ1和λ2是正則化參數(shù).直接求解式(8)非常困難,由于其中數(shù)據(jù)項和正則項依賴于不同的變量,因而采用交替方向法進行求解,可得到如下子問題:

(1)u的子問題求解.由于子問題式(9)的目標函數(shù)是可微的,對u求偏導,并將值設置為0,從而得到

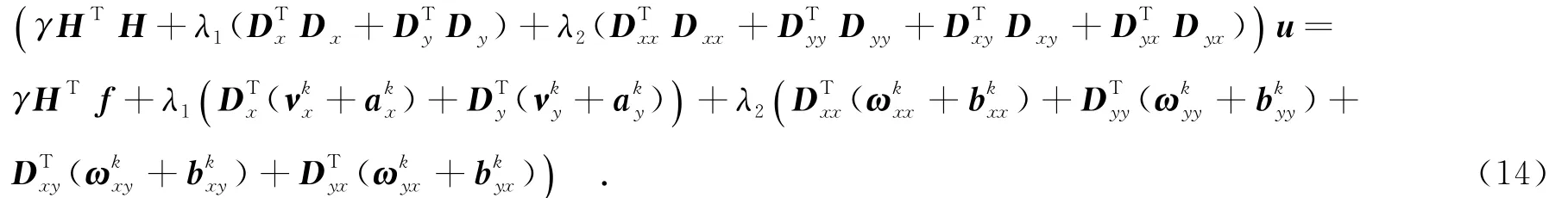
考慮到H及等式左邊均為分塊循環(huán)矩陣,且可用傅里葉變換對角化.式(14)利用傅里葉變換得到

(2)ν的子問題求解.針對式(10)的非凸問題最小化求解,采用p收縮算子實現(xiàn)[9-10],即

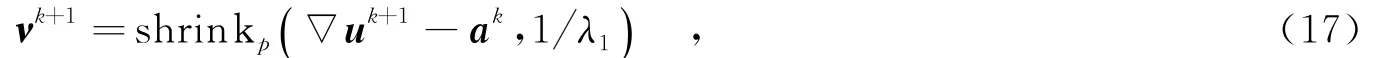
(3)ω的子問題求解.關于變量ω的求解,可直接采用shrinkage函數(shù)進行更新,即

最后,利用式(12)和式(13)對變量a和b進行更新.

1.2.2 模糊核h的求解

求解h時,固定u不變,得到

其中,U是圖像u矩陣表示.由變量分裂準則,引入輔助變量τ替代h,式(19)轉換為約束的優(yōu)化問題為

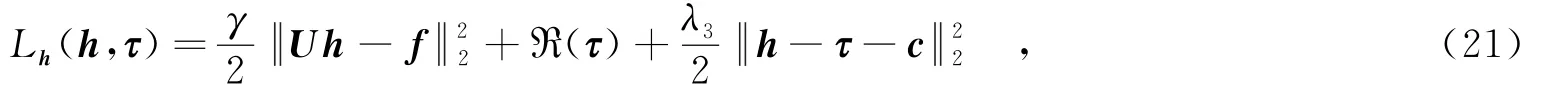
其中,c是擴展拉格朗日乘子,λ3是正則化參數(shù).類似于u的求解,采用交替方向法對式(21)求解,即

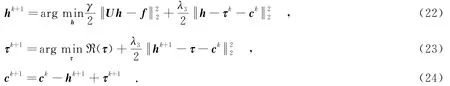
應用拉格朗日算法得到如下的目標函數(shù):

(1)h的子問題求解.通過傅里葉變換求解,得到

(2)τ的子問題求解,變量τ直接采用了soft-threshold函數(shù)進行求解,即

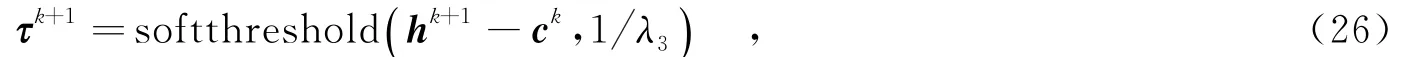
最后,利用式(24)對變量c進行更新.

2 實驗結果與分析

為驗證文中方法的有效性,分別針對人造模糊圖像和真實模糊圖像做出了兩組對比性實驗,對比的方法都是近年來在圖像盲復原領域中較為先進的方法.實驗中,參照文獻[6],將p取值為0.66.其余參數(shù)需要進行調(diào)節(jié),使復原結果達到最佳.

2.1 人造模糊圖像實驗

在人造模糊圖像實驗中,選擇了兩幅大小為512×512的標準測試圖像Lena和Peppers,人造模糊核兩種:勻速直線運動模糊核,長度為21,方向為135°(Kernel_1);自定義的不規(guī)則運動模糊核,大小為7×7 (Kernel_2).圖1和圖2顯示了文中方法與文獻[11]方法比較的視覺效果.圖1(b)和圖2(b)分別是由原始Lena圖像卷積Kernel_1,原始Peppers圖像卷積Kernel_2,同樣添加降晰信噪比(Blur Signal-to-Noise Ratio,BSNR)為40 d B的高斯噪聲得到的降質(zhì)圖像.文獻[11]方法構造了一個分段函數(shù)來擬合自然圖像的梯度分布,而提出的混合變分模型中的非凸項采用了高階拉普拉斯分布更為準確的擬合自然圖像的梯度分布.由兩種方法的復原圖像可看出,文中方法復原的圖像振鈴效應明顯減少,邊緣輪廓更加清晰.文獻[11]方法盲估計的模糊核的平滑擴散程度過強,而文中方法盲估計的模糊核更接近真實的模糊核.在客觀評價上,采用了峰值信噪比(Peak Siginalto Noise Ratio,PSNR)來衡量不同方法的圖像復原性能.表1給出了在BSNR 為40 dB時,兩種圖像盲復原方法的PSNR值,結果表明,文中方法的PSNR值相對于文獻[11]方法也有所提高.

圖1 Lena人造直線運動模糊圖像盲復原的結果

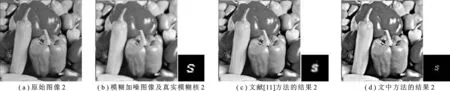
圖2 Peppers人造自定義不規(guī)則運動模糊圖像盲復原的結果

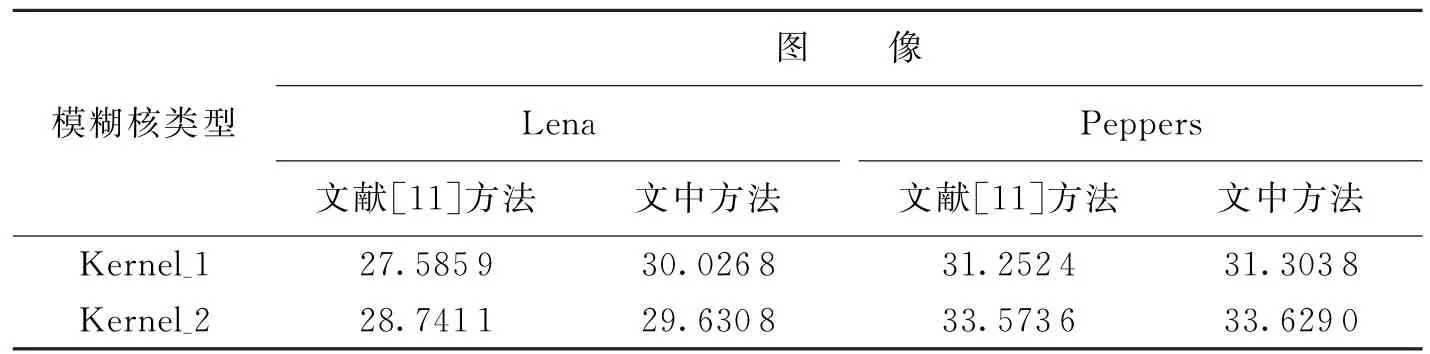
表1 不同方法的PSNR值比較結果　d B

2.2 真實模糊圖像實驗

為進一步驗證文中方法的實用性,選取了真實拍攝的模糊圖像Picasso進行復原實驗,并與文獻[12-13]方法進行比較.為更清晰地展示不同圖像盲復原方法的處理細節(jié),增加了局部放大圖.從結果來看,文獻[12]方法的復原圖像邊緣細節(jié)保持不夠好,文獻[13]方法的復原圖像優(yōu)于前者,但是去模糊后的圖像過于平滑,如Picasso臉部的皺紋等細節(jié)部分被平滑掉.而文中方法所產(chǎn)生的去模糊圖像顯示出更加尖銳的邊緣、清晰的輪廓,從整體上提升了圖像的視覺效果.

圖3 模糊圖像Picasso的復原結果對比

3 結束語

基于變分正則化方法提出了一種非凸混合總變分的模糊圖像盲復原方法,利用非凸lp擬范式作為一階總變分的稀疏約束,結合高階總變分在圖像平滑區(qū)域的擴散能力,建立一個非凸混合總變分的極小化模型.應用增廣拉格朗日方法和交替方向法進行優(yōu)化求解,得到清晰的復原圖像,同時準確地估計出模糊核函數(shù).求解中的非凸極小化問題利用了一種新的廣義p收縮算子,降低了此類問題的求解難度.實驗結果表明,文中方法能有效保護圖像邊緣和細節(jié),同時消除了平滑區(qū)域的階梯效應,得到了高質(zhì)量的復原圖像.

參考文獻:

[1]RUDIN L I,OSHER S,FATEMI E.Nonlinear Total Variation Based Noise Removal Algorithms[J].Physica D,1992,60(1/4):259-268.

[2]CHAN T F,WONG C K.Total Variation Blind Deconvolution[J].IEEE Transactions on Image Processing,1998,7(3):370-375.

[3]CHAMBOLLE A,LIONS P.Image Recovery via Total Variation Minimization Andrelatedproblems[J].Numerische Mathematik,1997,76(2):167-188.

[4]LYSAKER M,TAI X C.Iterative Image Restoration Combining Total Variation Minimizationand a Second-order Functional[J].International Journal of Computer Vision,2006,66(1):5-18.

[5]PAPAFITSOROS K,SCHONLIEB C B.A Combined First and Second Order Variational Approach for Image Reconstruction [J].Journal of Mathematical Imaging and Vision,2014,48(2):308-338.

[6]KRISHNAN D,FERGUS R.Fast Image Deconvolution Using Hyper-Laplacian Priors[C]//Advances in Neural Information Processing Systems.New York:Curran Associates Incorporated,2009:1033-1041.

[7]NIKOLOVAM,NG M K,TAM C P.Fast Nonconvex Nonsmooth Minimizationmethods for Image Restoration and Reconstruction[J].IEEE Transactions on Image Processing,2010,19(12):3073-3088.

[8]張文娟,馮象初.利用平衡方法的非凸圖像修復[J].西安電子科技大學學報,2014,41(5):141-147.ZHANG Wenjuan,FENG Xiangchu.Nonconvex Image Inpainting via Balanced Regularization Approach[J].Journal of Xidian University,2014,41(5):141-147.

[9]CHARTRAND R.Nonconvex Splitting for Regularized Low-Rank+Sparsedecomposition[J].IEEE Transactions on Signal Processing,2012,60(11):5810-5819.

[10]張文娟,馮象初.非凸低秩稀疏約束的圖像超像素分割方法[J].西安電子科技大學學報,2013,40(5):86-91.ZHANG Wenjuan,FENG Xiangchu.Image Super-pixels Segmentation Method Based on the Non-convex Low-rank and Sparse Constraints[J].Journal of Xidian University,2013,40(5):86-91.

[11]SHAN Q,JIA J,AGARWALA A.High-quality Motion Deblurring from a Single Image[J].ACM Transactions on Graphics,2008,27(3):73.

[12]KRISHNAN D,TAY T,FERGUS R.Blind Deconvolution Using a Normalized Sparsity Measure[C]//Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Piscataway:IEEE,2011:233-240.

[13]XU L,JIA J Y.Two-phase Kernel Estimation for Robust Motion Deblurring[C]//Lecture Notes in Computer Science: 6311 LNCS.Heidelberg:Springer Verlag,2010:157-170.

(編輯:齊淑娟)

Non-convex hybrid total variation method for image blind restoration

LIU Qiaohong1,LI Bin1,LIN Min2
(1.School of Mechatronic Engineering and Automation,Shanghai Univ.,Shanghai 200073,China;2.Department of Medical Electronics and Information Engineering,Shanghai Medical Instrumentation College,Shanghai 200093,China)

Abstract:A multi-regularization constraint method for imageblind restoration is proposed to recover the blurry-noisy images.First,the non-convex total variation is adoptedas the regularization constraint by taking the sparse edges in the natural image into consideration.Next,the high-order total variation is used to overcome the staircase effects in the smooth regions of the image.Then a non-convex minimization model is proposed.Finally,the augmented Lagrangian method and a new generalized p shrinkage operator are applied to solve the model.The results of numerical experiments show that the proposed method can preserve the image edges while removing the staircase effects effectively.The high quality restored image can be obtained.

Key Words:image restoration;non-convex;high-order;total variation;augmented Lagrangian method;p shrinkage operator;optimization

作者簡介:劉巧紅(1979-),女,講師,上海大學博士研究生,E-mail:hqllqh@163.com.

基金項目:上海市教育委員會科研創(chuàng)新資金資助項目(14YZ169)

收稿日期:2014-12-23 網(wǎng)絡出版時間:2015-05-21

doi:10.3969/j.issn.1001-2400.2016.02.021

中圖分類號:TP751.1

文獻標識碼:A

文章編號:1001-2400(2016)02-0120-06

網(wǎng)絡出版地址:http://www.cnki.net/kcms/detail/61.1076.TN.20150521.0902.018.html