圖像融合對圖像中信號頻率影響的研究

段　偉，閆　利,鞏翼龍

(武漢大學測繪學院，湖北 武漢 430079)

?

圖像融合對圖像中信號頻率影響的研究

段偉，閆利,鞏翼龍

(武漢大學測繪學院，湖北 武漢 430079)

Research on Influence of Image Fusion on Signal Frequency

DUAN Wei,YAN Li，GONG Yilong

摘要：圖像融合是圖像處理的重要步驟之一，本文分析了多種圖像融合方法，根據高采樣率奈奎斯特頻率、低采樣率奈奎斯特頻率和信號頻率三者之間的關系，對圖像融合前后信號頻率的變化進行了研究，試驗結果表明圖像融合對低采樣率圖像的識別能力有一定的提升。

關鍵詞：圖像融合；信號頻率；傅里葉變換；奈奎斯特頻率

遙感圖像融合是將不同傳感器對同一目標獲取的圖像經過一定的處理方式最終綜合成一幅圖像的技術。其中最典型的應用即遙感影像中全色圖像與多光譜圖像的融合，融合后的圖像能更加全面地描述所研究的對象[1-2]。融合之后信號頻率會發生怎樣的變化也是人們重點關注的問題。目前，人們關注比較多的問題是圖像融合的方法和融合后的圖像質量，而對圖像中信號頻率的變化研究較少。本文結合多種圖像融合方法對圖像融合前后信號頻率的變化進行了研究，試驗結果表明圖像融合后能使水平方向和垂直方向信號頻率位于高采樣率奈奎斯特頻率和低采樣率奈奎斯特頻率之間的信號在圖像上得到一定的呈現，對低采樣率圖像的識別能力有一定的提升。

一、圖像融合

圖像融合的方法眾多，不同的融合方法得到的融合效果也各不相同，選擇合適的融合方法對最終獲得高質量的融合圖像有非常重要的影響[3-4]。目前基于像元的融合方法中較為常見的有基于空間域的濾波融合算法(如HPF融合算法)、基于頻率域的濾波融合算法(如Ehlers融合)、基于小波變換的融合算法(如DBSS小波融合、haar小波融合)、基于統計分析的融合算法(如PanSharp全色銳化融合)、基于代數運算的融合算法(如PCA變換融合、Gram-Schmidt變換融合、Brovey變換融合、乘法變換融合、對比度金字塔融合、FSD金字塔融合、梯度金字塔融合、拉普拉斯金字塔融合、形態差異金字塔融合、比率金字塔融合等)、基于彩色空間的融合算法(如HIS變換融合算法)等。這些融合算法有各自不同的特點和優勢，如PanSharp方法可以保留最豐富的細節信息[5]，Gram-Schmidt變換融合算法可以獲得最佳的光譜保真度[6]，HPF融合算法有較快的運算速度[7]。針對不同的遙感圖像要選擇合適的融合算法，以得到最佳的融合效果。

二、信號頻率分析

本文采用水平方向的圖像信號作為重點研究對象，使用傅里葉變換將圖像信號從空域轉化到頻域，對圖像融合前后的信號頻率進行分析。傅里葉原理表明：任何連續測量的時序或信號都可以表示為不同頻率的正弦波信號的無限疊加。而根據該原理創立的傅里葉變換算法利用直接測量到的原始信號，以累加方式來計算該信號中不同正弦波信號的頻率、振幅和相位[8-10]。在實際應用中，進行融合的圖像頻率往往是沒有固定范圍的，而且融合之前要進行配準和重采樣的過程。根據奈奎斯特定理，需要離散系統的奈奎斯特頻率高于被采樣信號的最高頻率或帶寬才能避免混疊現象。本文對高采樣率奈奎斯特頻率、低采樣率奈奎斯特頻率和信號頻率三者之間的關系進行分類討論。

三、試驗

根據高采樣率奈奎斯特頻率、低采樣率奈奎斯特頻率和信號頻率的關系，分高采樣率奈奎斯特頻率和低采樣率奈奎斯特頻率均大于信號頻率、信號頻率位于高采樣率奈奎斯特頻率和低采樣率奈奎斯特頻率之間及高采樣率奈奎斯特頻率和低采樣率奈奎斯特頻率均小于信號頻率3種情況進行討論。

1. 高采樣率奈奎斯特頻率和低采樣率奈奎斯特頻率均大于信號頻率

設試驗中圖像信號的頻率為10 Hz，幅度為1，信號長度為固定值，高采樣頻率為256 Hz，低采樣頻率為128 Hz，如圖1所示。其對應的幅度-頻率曲線如圖2所示。

圖1　高采樣率圖像與低采樣率圖像

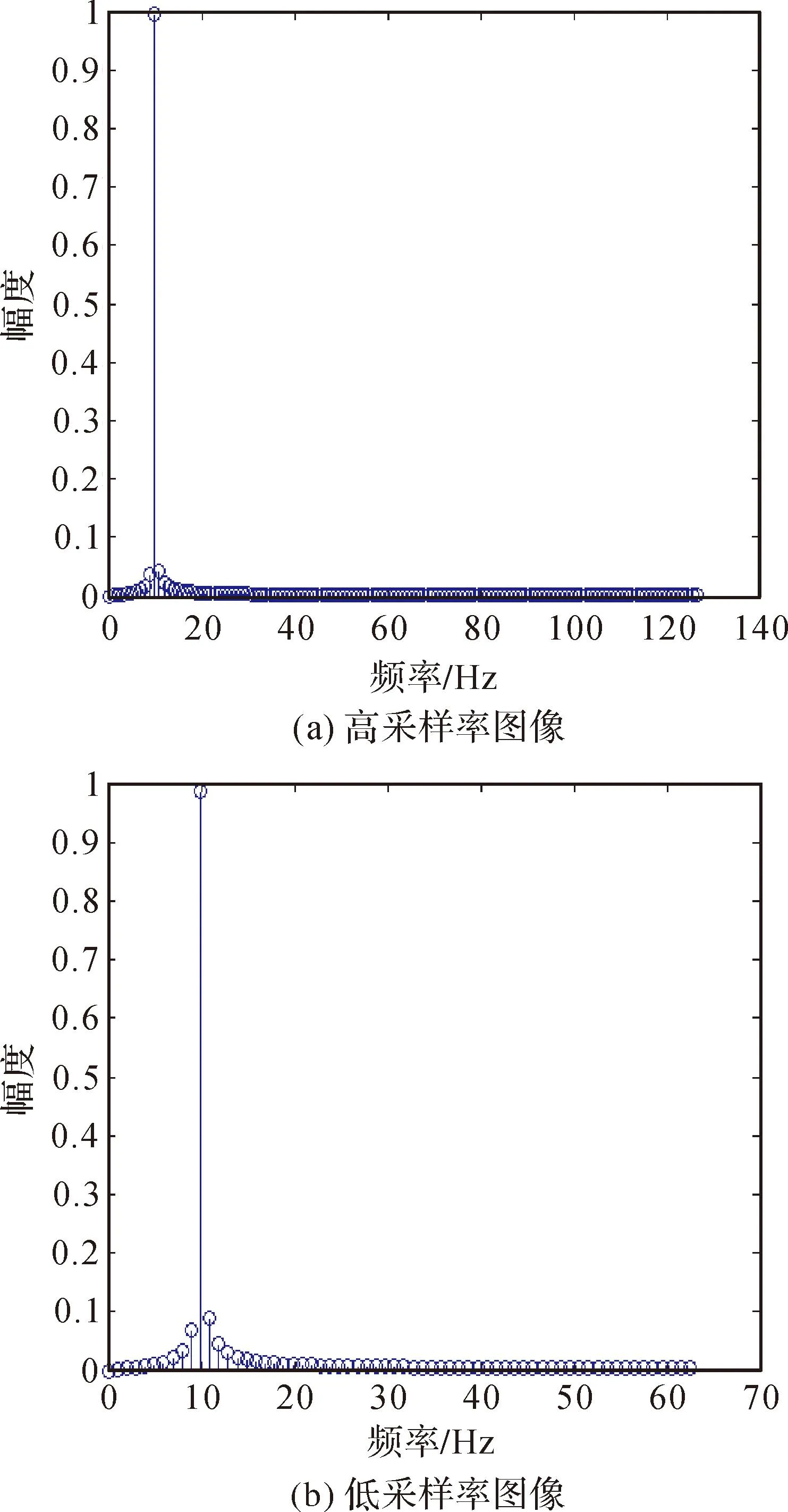
圖2　高采樣率圖像和低采樣率圖像的幅度-頻率圖

從圖中可以看出，高采樣率圖像與低采樣率圖像中信號頻率相同。融合之前要對低采樣率圖像進行重采樣，以達到與高采樣率相同的采樣率，重采樣后的圖像頻率與重采樣前相同。將高采樣率圖像與重采樣后的圖像進行haar小波融合，得到的圖像與幅度-頻率圖如圖3所示。由圖3可以發現，融合后信號的頻率沒有發生變化，即高采樣率奈奎斯特頻率和低采樣率奈奎斯特頻率均大于信號頻率的情況下圖像融合的處理不會影響圖像中的信號頻率。

圖3　融合后的圖像與幅度-頻率圖

2. 信號頻率位于高采樣率奈奎斯特頻率和低采樣率奈奎斯特頻率之間

設試驗中圖像信號的頻率為100 Hz，幅度為1，信號長度為固定值，高采樣頻率仍為256 Hz，低采樣頻率仍為128 Hz，其對應的幅度-頻率曲線如圖4所示。

可以看出高采樣率圖像能夠準確獲取信號頻率，而低采樣率圖像因為欠采樣得到的信號頻率已與原信號不同，對其進行重采樣，將高采樣率圖像與重采樣后的低采樣率圖像進行haar小波融合，得到圖像的幅度-頻率圖如圖5所示。由圖5可以發現，融合后信號的頻率有兩個峰值。這是因為低采樣率的圖像欠采樣導致其不能準確獲得信號頻率，使本應該在同一頻率下進行的圖像融合在不同頻率的信號之間進行，而融合的過程是對分解后的不同子帶系數采用合適的融合規則進行融合，兩種不同的頻率都會融合進圖像中，同時幅度相較于融合前會有所降低。通過試驗也可以看到兩種不同頻率的圖像在進行融合之后所得到的圖像會同時包含融合前的兩種不同頻率。

圖4　高采樣率圖像和低采樣率圖像的幅度-頻率圖

3. 高采樣率奈奎斯特頻率和低采樣率奈奎斯特頻率均小于信號頻率

設試驗中圖像信號的頻率為200 Hz，幅度為1，信號長度為固定值，高采樣頻率為256 Hz，低采樣頻率為128 Hz，其對應的幅度-頻率曲線如圖6所示。

圖6　高采樣率圖像和低采樣率圖像的幅度-頻率圖

從圖6中可以看到，因為欠采樣高采樣率圖像和低采樣率圖像得到的信號頻率均與目標信號的頻率不同，對低采樣率圖像進行重采樣，將高采樣率圖像與重采樣后的圖像進行haar小波融合，得到圖像的幅度-頻率圖如圖7所示。

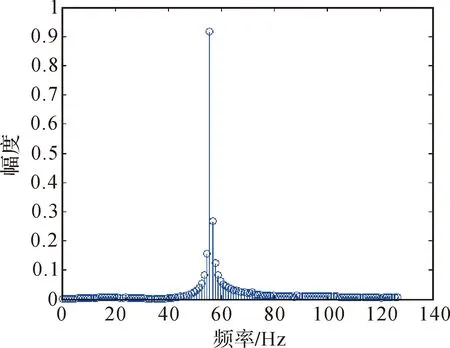
圖7　融合后的幅度-頻率圖

由圖7可以發現，雖然融合后的頻率與信號頻率不同，但仍具有唯一的頻率，這是因為高采樣率正好是低采樣率的兩倍，將低采樣率變為120 Hz，重復前面的融合過程，得到的融合后圖像的幅度-頻率圖如圖8所示。

圖8　融合后的幅度-頻率圖

由圖8可以看到，當高采樣率和低采樣率不滿足兩倍關系時，融合后的圖像將同時具有兩種信號頻率。

以上試驗采用的融合方法為haar小波融合，在使用對比度金字塔融合、梯度金字塔融合、拉普拉斯金字塔融合、FSD金字塔融合、PCA方法融合、比率金字塔融合、DBSS小波融合等方法進行融合時也能得到相同的試驗結果。

四、結論

通過上面的試驗可以得到以下結論：

1) 當高采樣率奈奎斯特頻率和低采樣率奈奎斯特頻率均大于圖像信號頻率時，融合后圖像的信號頻率不會發生變化。

2) 圖像信號頻率位于高采樣率奈奎斯特頻率和低采樣率奈奎斯特頻率之間時，融合之后圖像不再是由單一頻率構成，而是由兩種不同的頻率混合構成，頻率中會包含高采樣率所獲得的原始信號頻率。

3) 高采樣率奈奎斯特頻率和低采樣率奈奎斯特頻率均小于圖像信號頻率時， 融合后無法得到圖像中的信號頻率。當高采樣率是低采樣率的兩倍時，融合后能得到唯一的頻率，否則融合后的圖像由兩種不同的頻率構成。

4) 對低采樣率的圖像而言，與高采樣率的圖像融合后能使水平方向和垂直方向信號頻率位于高采樣率奈奎斯特頻率和低采樣率奈奎斯特頻率之間的信號在圖像上得到一定的呈現，使原始的信號頻率得到了恢復，從這個角度來說，可以認為圖像融合在一定程度上提升了低采樣率圖像的識別能力。

參考文獻：

[1]黃愛民，安向東.數字圖像處理與分析基礎[M].北京：中國水利水電出版社，2005.

[2]趙蓉椿，趙忠明.數字圖像處理導論[M].西安：西北工業大學出版社，2005.

[3]李小春.多源遙感影像融合技術及應用研究[D]. 鄭州:信息工程大學，2005.

[4]孫曉霞，張繼賢，高井祥,等.基于IHS變換和非下采樣Coutourlet變換的不同波段多極化SAR圖像融合[J].測繪通報，2011(6)：1-4.

[5]譚永生.中高分辨率遙感影像融合研究[J].遙感技術與應用，2007,22(4):536-542.

[6]趙珍梅，馬偉，王潤生.三種高保真遙感影像融合方法效果評價與分析[J].地質與勘探，2010,46(4):705-710.

[7]李平湘，王智均.高空間分辨率影像和多光譜影像融合的研究[J].武漢大學學報(信息科學版),2003,28(1):14-17.

[8]BRACEWELL R N.The Fourier Transform and Its Application[M].New York:McGraw-Hill, 1986.

[9]PROAKIS J G,MANOLAKIS D G.Introduction to Digital Signal Processing[M].New York: Macmillan Publishing Company,1988.

[10]蔣長錦，蔣勇.快速傅里葉變換及C程序[M].合肥：中國科技大學出版社，2004.

中圖分類號：P237

文獻標識碼：B

文章編號：0494-0911(2016)03-0036-04

作者簡介：段偉(1987—)，男，博士生，研究方向為遙感圖像處理。E-mail: 422901445@qq.com

基金項目：國家自然科學基金(41271456)

收稿日期：2015-02-16

引文格式： 段偉，閆利,鞏翼龍. 圖像融合對圖像中信號頻率影響的研究[J].測繪通報，2016(3)：36-39.DOI:10.13474/j.cnki.11-2246.2016.0081.