基于卡爾曼濾波的空氣質量指數預測方法

南亞翔，李紅利，修春波，張洪志

(1.天津工業大學電氣與自動化學院，天津 300387；

2.天津工業大學電工電能新技術天津市重點實驗室,天津 300387；

3.中國石油大港油田原油運銷公司，天津 300280)

?

基于卡爾曼濾波的空氣質量指數預測方法

南亞翔1,2，李紅利1,2，修春波1,2，張洪志3

(1.天津工業大學電氣與自動化學院，天津 300387；

2.天津工業大學電工電能新技術天津市重點實驗室,天津 300387；

3.中國石油大港油田原油運銷公司，天津 300280)

摘要：分析了卡爾曼濾波預測空氣質量指數的機理，用ARMA算法為卡爾曼濾波建立模型，提出了將RBF神經網絡融合于卡爾曼濾波的方法，實現對空氣質量指數的混合預測。根據空氣質量指數時間序列的特點，建立了自回歸預測模型，進而建立卡爾曼濾波的狀態方程和測量方程。采用隨機梯度逼近訓練算法訓練RBF神經網絡，用RBF神經網絡的輸出作為卡爾曼濾波測量方程的觀測值。融合了RBF神經網絡后的卡爾曼濾波預測方法減少了單一方法的延遲現象，使同種性質的誤差累積減小，提高了預測精度。對AQI序列預測的仿真顯示融合后的卡爾曼濾波方法優于單一的卡爾曼濾波方法，亦優于現已廣泛應用的BP神經網絡預測方法。

關鍵詞：卡爾曼濾波；空氣質量指數；預測；ARMA；RBF神經網絡

近年來城市空氣污染嚴重，民眾對空氣質量日益關注。環保部門對AQI(空氣質量指數)數據進行通報時，由于大氣空間屬于純滯后系統，因此通報的數據具有滯后性，實時性較差，不能夠滿足一些戶外作業和特定工作人員的需求。AQI指數預測可以解決通報數據滯后性問題。由于空氣污染物濃度受到污染排放源、理化生過程和復雜下墊面等因素的影響，因此具有強非線性特性[1]。人工神經網絡是描述非線性系統的有效工具，其中BP神經網絡作為使用最為廣泛的神經網絡之一，有很強的泛化能力和容錯能力，亦能夠很好地描述污染指數與其影響因子之間的非線性關系，十分簡單可行，已經被廣泛應用在PM10、SO2、NOx等污染物濃度的預測當中[2-6]。但BP神經網絡具有誤差較大，訓練時容易陷入局部最小值等缺點，預測效果不佳[7]。本文分析了ARMA建模方法和卡爾曼濾波數據預測及融合的機理，提出了將RBF(徑向基函數)神經網絡預測數據融合在卡爾曼濾波的方法，克服了單一方法預測的不足，提高了AQI指數預測的精度。

1基于卡爾曼濾波的AQI指數預測

1.1由ARMA模型建立線性離散動態系統模型

時間序列最優預報的基本數學模型是自回歸滑動平均模型[8]，在ARMA模型中，時間序列{x(t)}具有以下形式：

xt-φ1xt-1-…-φpxt-p=at-θ1at-1-…θqat-q

(1)

(2)

xt=φ1xt-1+φ2xt-2+φpxt-p+εt

(3)

則系統的狀態方程及測量方程可以寫為：

(4)

(5)

1.2卡爾曼濾波的基本原理

卡爾曼濾波本質上是給出了一種遞推算法，由實時獲得的離散觀測數據，對系統狀態進行線性、無偏及最小誤差方差的最優估計[9]。應用卡爾曼濾波首先要建立線性模型。通常情況下，線性離散動態系統可以由以下狀態方程和觀測方程表示：

(6)

Z(t)=H(t)X(t)+v(t)

(7)

其中：t是離散時間；Φ(t,t-1)是從t-1時刻到k時刻的狀態轉移矩陣；Γ(t,t-1) 是從t-1時刻到t時刻的激勵轉移矩陣；H(t)是t時刻的預測輸出轉移矩陣；w(t)是p維系統噪聲向量；v(t)是m維觀測噪聲向量；x(t)是n維狀態向量；Z(t)是m維觀測向量。

在卡爾曼濾波方程中，假設w(t)、v(t) 為高斯白噪聲。它們的協方差矩陣分別設為Q(t)和R(t)，一般情況下Q(t)和R(t)的值按經驗取。卡爾曼濾波首先針對無控制輸入系統求解，再通過疊加確定性求解，最終得到的遞推預測方程如下：

(8)

(9)

(10)

(11)

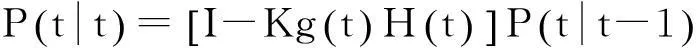
(12)

1.3基于神經網絡觀測值的獲取

為了克服用單一方法對空氣污染指數預測的不足，本文將神經網絡獲得數據的觀測值Z(t)代入到卡爾曼濾波方程中，從而將神經網絡融合在卡爾曼濾波當中，實現混合預測。

神經網絡系統實質上是由大量的神經單元廣泛地互相連接而形成的復雜的網絡系統，具有學習功能。可以處理難以用模型或規則描述的過程和系統，并且具有很強的容錯性[11，12]。本文采用RBF神經網絡對空氣污染指數數據進行預測。

RBF神經網絡是一種前向型神經網絡，網絡由三層組成，即輸入層、單層的非線性處理神經元和輸出層。與現今應用較為廣泛的BP神經網絡相比，具有更快的學習收斂速度，良好的泛化能力，結構簡單，有最佳逼近性能和全局最優特性等優點。RBF的輸出層一般滿足：

(13)

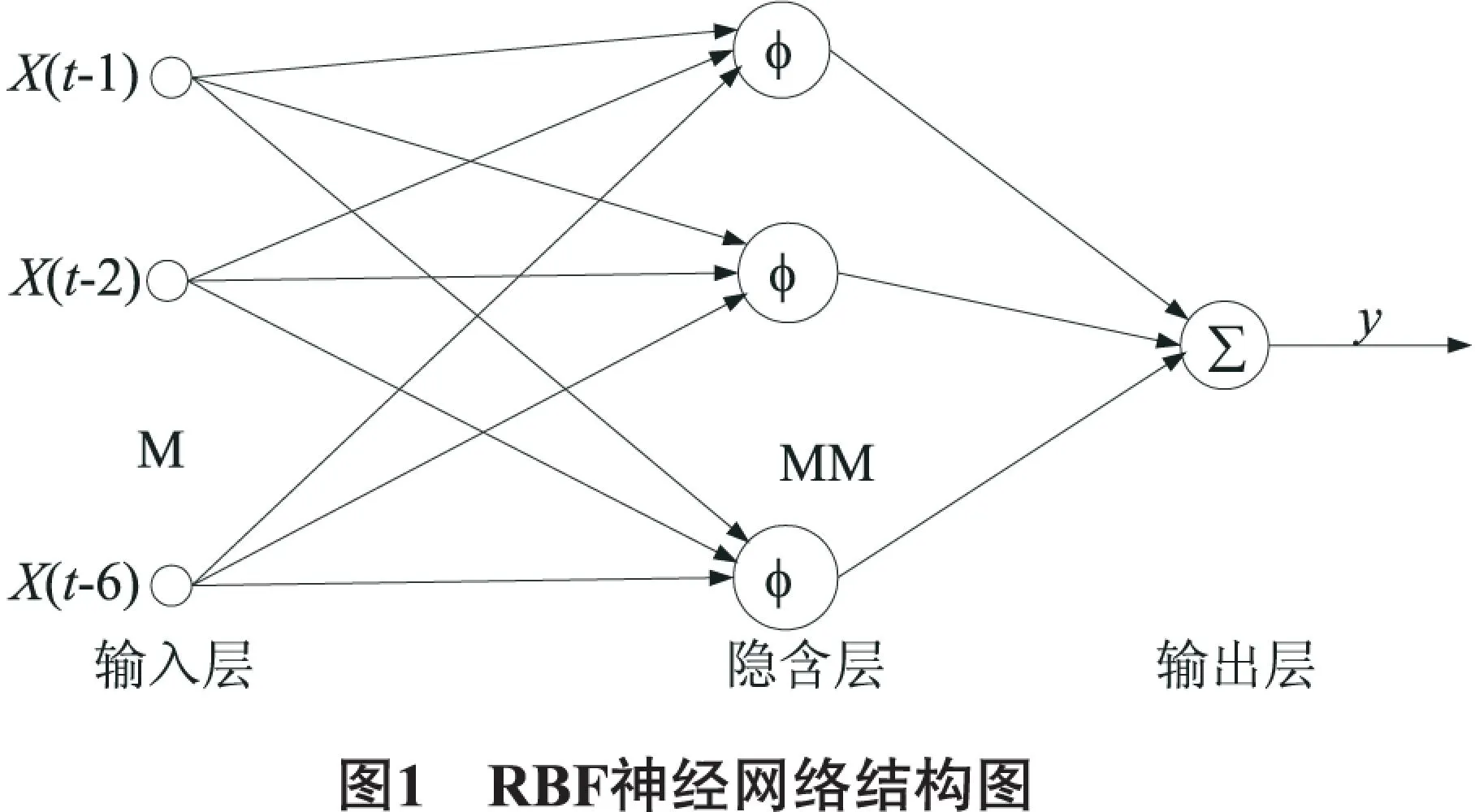
用已知的AQI數據序列作為訓練樣本集，為了避免因為從輸出數據集中選取大量的中心，進而產生相對龐大的網絡，本文采用隨機梯度訓練算法。

隨機梯度法在訓練RBF神經網絡時使輸出層的加權值w、中心點值c和擴展參數同步進行有導師學習，即

(14)

(15)

(16)

其中：

(17)

(18)

2數據來源

根據2012年中華人民共和國環境保護部發布的《環境空氣質量指數(AQI)技術規定(試行)》，地級以上(含地級)環境保護行政主管部門或其授權的環境監測站開始向公眾對AQI指數進行實時報和日報。研究使用的數據為中華人民共和國環境保護部數據中心發布的天津市2013年上半年連續90h的AQI數據。

表1　空氣質量指數及相應質量級別

空氣質量指數級別根據表1規定進行劃分。與之前廣泛使用的空氣污染指數(API)相比，環境空氣質量指數將可吸入細顆粒物(PM2.5)等污染物納入了測量通報范圍，相比之下AQI評價結果更真實地反映了空氣質量實際情況。隨著納入考核的污染物種類的增多和計算方法復雜程度的加大，AQI指數受到更多因素的影響，具有較強的非線性特性。

3對AQI指數預測的仿真和分析

3.1卡爾曼濾波對AQI指數的預測

本文選取了天津市2014年上半年某星期連續90h的時報AQI指數作為實驗數據。由于每年相同時節影響AQI指數的自然因素(大氣溫度、濕度等)較為相似，選取天津市2013年上半年1—5月份時報AQI指數作為RBF神經網絡的訓練樣本，6月份的時報AQI指數作為測試樣本，用于對RBF神經網絡預測性能的檢驗。

由圖3可以看出，通過ARMA算法建立模型的卡爾曼濾波方法能夠對AQI指數進行預測。預測的結果能夠大體反映AQI指數的變化趨勢，但存在較大的滯后延遲現象，致使預測結果的誤差較大，并未達到理想的預測結果。

3.2基于BP神經網絡對AQI指數的預測

用BP神經網絡對AQI指數進行預測，得到的預測樣本如圖4。

由圖4可見，BP神經網絡預測算法在某些點處有較強的非線性逼近能力，具有一定的預測能力和預測精度，但在指數波動較大的極點處，誤差較大。即空氣指數的波動對BP神經網絡的泛化能力有影響，影響了預測的效果和預測精度。

3.3基于RBF神經網絡和卡爾曼濾波混合算法對AQI指數的預測

將RBF神經網絡的預測結果作為卡爾曼濾波方程的觀測值，實現AQI指數的混合預測，所得預測結果如圖5所示。

由圖5可見，卡爾曼濾波能夠將ARMA方法和RBF神經網絡方法進行融合，從而可進一步優化預測結果，預測結果優于單一采用RBF神經網絡的預測結果和單一的卡爾曼濾波預測方法。融合的預測方法與RBF神經網絡預測結果相比，延遲現象得到了極大的改善；與BP神經網絡預測方法相比，在數據序列極值點的預測結果誤差大大減小，預測效果有明顯改善。不同方法預測誤差指標如表2所示。

從表2誤差比較結果可見，BP神經網絡對AQI指數的預測結果有較大的誤差，這是因為單一的BP神經網絡中神經元對歷史信息的記憶能力和利用率有限，對數據原狀態的保持能力不佳，從而增加了神經元狀態錯誤變化的機率。單一的卡爾曼濾波預測方法具有單一預測機理所造成的同一性質誤差的累積，因此誤差亦較大。融合的卡爾曼濾波方法將卡爾曼濾波和RBF神經網絡結合，吸收了RBF神經網絡良好的泛化能力、學習速度快、容易適應新數據的優點和卡爾曼濾波預測模型所利用的信息量較少、對初始量數據要求不高的優點，大大增強了預測的精度，從而減少了預測誤差。

表2　不同方法預測性能指標

4結論

(1) 本文提出并分析了卡爾曼濾波方法對AQI指數的預測機理，對不同預測方式的預測性能進行了分析比較。用ARMA模型建立卡爾曼濾波的狀態方程和觀測方程，利用RBF神經網絡的預測值作為卡爾曼濾波方程的觀測值，進而用卡爾曼濾波方法將ARMA和RBF神經網絡融合在一起，實現了AQI指數的混合預測。

(2)仿真實驗結果驗證了混合預測方法的有效性，該混合預測方法能有效減小單一預測方法造成的誤差積累，并減少極值點等有較大波動數據點的誤差。融合后的方法獲取了2種方法的優點，預測結果十分理想。

參考文獻：

[1]李小飛,張明軍,王圣杰,趙愛芳,馬潛. 中國空氣污染指數變化特征及影響因素分析[J]. 環境科學,2012(6):1936-1943.

[2]白曉平,張啟明,方棟, 等.人工神經網絡在蘇州空氣污染預報中的應用[J].科技導報, 2007, 25(3): 45-49.

[3]曹蘭.空氣中PM10濃度的BP神經網絡預報研究[J].環境研究與監測, 2010, 23(2): 29-32.

[4]王儉, 胡筱敏, 鄭龍熙, 等. 基于BP模型的大氣污染預報方法的研究[J].環境科學研究, 2002, 15(5): 62-64.

[5]白鶴鳴,沈潤平,師華定,董鈺春. 基于BP神經網絡的空氣污染指數預測模型研究[J]. 環境科學與術,2013(3):186-189.

[6]周秀杰,蘇小紅,袁美英. 基于BP網絡的空氣污染指數預報研究[J]. 哈爾濱工業大學學報,2004(5):582-585.

[7]Kalman R E. A New Approach to Linear Filtering and Prediction Theory. Trans ASME Journal of Basic Eng . 1960

[8]張賢達. 確定ARMA模型MA階數的一種方法[J]. 自動化學報,1994(1):80-84.

[9]修春波,任曉,李艷晴,劉明鳳. 基于卡爾曼濾波的風速序列短期預測方法[J]. 電工技術學報,2014(2):253-259.

[10]王學林,周俊,姬長英,姜莉. 基于卡爾曼濾波的RBF神經網絡和PD復合控制研究[J]. 計算機測量與控制,2009(8):1551-1553,1573.

[11]劉進寶,丁濤. 基于徑向基函數神經網絡的風速預測[J]. 太陽能學報,2012(7):1131-1135.

[12]Y. F. Sun,Y. C. Liang,W. L. Zhang,H. P. Lee,W. Z. Lin,L. J. Cao. Optimal partition algorithm of the RBF neural network and its zapplication to financial time series forecasting[J]. Neural Computing and Applications, 2005 (1).

Prediction Method of Air Quality Index Based on Kalman Filtering Fusion

NAN Ya-Xiang1,2, LI Hong-Li1,2, XIU Chun-Bo1,2, ZHANG Hong-Zhi3

(1.Tianjin Polytechnic University, College of Electrical Engineering and Automation, Tianjin 300387, China)

Abstract：The prediction mechanism ofKalman filtering for air quality index was analyzed. And a hysteretic neural network was proposed to predict the air quality index series. State equation for Kalman filter was established by ARMA model. The hybrid prediction of air quality index, combining Kalman filter and RBF neural network was proposed. According to the characteristic of air quality index series, autoregressive model was established. And then, the measurement equation and the state equation of Kalman filter were established as well. Stochastic gradient approximation method was applied to train RBF neural network. The output of RBF neural network was regarded the observed value by Kalman filter. Hybrid prediction’s main advantages included preventing forecast delay caused by the single prediction mechanism and precise forecasting. The results of predicting air quality index simulation showed that the hysteretic Kalman filter had better prediction performance than original Kalman filter, and the hysteretic Kalman filter was also superior to BP neural network.

Key words：Kalman filter; air quality index; prediction; ARMA; RBF neural network

中圖分類號：X 823

文獻標志碼：A

文章編號：1673-9655(2016)03-0080-05

作者簡介：南亞翔(1990-)，男，遼寧鐵嶺人，碩士研究生，主要研究智能控制系統與數據挖掘。

基金項目：國家自然科學基金項目(No.61203302);天津市應用基礎與前沿技術研究計劃項目(14JCYBJC18900)。

收稿日期：2015-10-10