基于多維gPC的船舶電力推進系統仿真不確定性分析

劉 勝 程垠鐘

（哈爾濱工程大學自動化學院 哈爾濱 150001）

?

基于多維gPC的船舶電力推進系統仿真不確定性分析

劉 勝 程垠鐘

（哈爾濱工程大學自動化學院 哈爾濱 150001）

摘要為了解決在船舶電力推進系統設計研發過程中面臨不確定性因素較多的問題，將廣義多項式混沌（gPC）應用到系統仿真的不確定性分析中，并通過張量積將一維的gPC擴展到了多維。通過在一階隨機微分方程中的應用，驗證了方法的有效性。在此基礎上，對船舶電力推進系統在多個隨機變量共同影響下的響應進行了建模、仿真和不確定性分析，得到了系統響應的統計特性。研究結果表明，構建的多維廣義多項式混沌能夠有效地對船舶電力推進系統在多個不確定因素共同影響下的響應進行定量的不確定性分析。在多個隨機變量的共同影響下，系統的動態過程和穩態過程都將受到影響，在過渡過程中將會出現影響最嚴重的時刻，從而為設計研發提供參考。

關鍵詞：船舶電力推進 仿真 不確定性分析 廣義多項式混沌

國家自然科學基金資助項目（51279036）。

0 引言

隨著電力電子技術、現代控制理論及其他相關技術的發展，船舶電力推進系統越來越受到世界各國的關注和重視。船舶電力推進使得船舶的推進系統和電力系統有機結合在一起[1]，能夠給船舶帶來一系列優點，包括電能的合理分配、有效倉容的增加、隱身性和舒適性的提高等[2]。然而，與船舶電力推進系統的優點相對應的是在系統設計研發過程中需要面對的諸多不確定性。船舶電力推進系統的推進電機與螺旋槳同軸連接，由于受到隨機海浪的影響，作用于電動機軸上的負載轉矩也將是隨機的，這種不確定性必然會對船舶電力推進系統的運行產生影響[3]。此外，時變的電動機參數，如受溫度變化影響的電阻、軸承的摩擦及鐵磁材料的飽和等都使船舶電力推進系統的不確定性影響更加嚴重[4]。

動態仿真的不確定性分析方法適于定量分析包含不確定參數的隨機系統，目前已經在陸地電力系統的仿真中得到了一定的應用[5-7]，而在船舶電力推進系統這樣一個獨立的且受不確定性因素影響嚴重的系統中還沒有得到廣泛應用。不確定性分析方法主要分為兩大類：統計方法和非統計方法。

傳統的不確定性仿真分析方法如蒙特卡洛法[8]等存在仿真次數多、仿真時間長的缺點。廣義多項式混沌（generalized Polynomial Chaos，gPC）是一種非統計方法，起源于R.G.Ghanem等在解決隨機力學的多種問題中在多項式混沌展開方面進行的研究[9]。D.Xiu等在其基礎上進行了擴展，從而提出了廣義多項式混沌[10]，證明了存在最優的正交多項式與不同概率密度的變量相對應，可以根據隨機輸入確定隨機變量的概率密度，根據隨機輸入的權重函數選擇對應的正交多項式。gPC方法目前已經應用在求解隨機常微分方程（Ordinary Differential Equation,ODE）、偏微分方程以及計算流體力學的不確定性分析方面[11]，在控制理論和電路分析等方面也有初步應用[12,13]。研究結果表明，gPC方法與傳統方法相比，能夠顯著提高分析的效率。國內在gPC方面的研究也已經開展，王曉東等采用該方法求解了隨機Burgers方程，介紹了其與流體力學的耦合過程，驗證了gPC在隨機流動模擬中的有效性[14]；韓冬等應用隨機響應面法開展了針對陸地電力系統的動態仿真不確定性分析研究[15]，隨機響應面法也屬于gPC方法的應用范疇，其采用了概率配點的方式進行多項式混沌系數的求解，研究結果表明隨機響應面法能夠克服傳統不確定性分析方法的缺點。到目前為止，尚沒有文獻在多個不確定性參數共同影響下定量地進行系統仿真的不確定性分析。

本文為了解決存在的問題，將gPC方法應用到船舶電力推進系統的動態仿真研究中，并采用張量積構建多維gPC基底，結合Galerkin映射[10]進行多項式混沌系數的求解。通過使用該方法，能夠實現對多項式混沌維數的擴展，從而實現對船舶電力推進系統在多個不確定性參數共同影響下的隨機響應進行定量分析的目的。

1 廣義多項式混沌

對于任意一個二階隨機變量u（ω），都可以使用廣義多項式混沌展開表示為

式中，δij為克羅尼克-Δ函數；為Hilbert空間的內積。有

式中，W（ξ）為權函數。

Askey法則中隨機變量的概率密度與最優正交多項式的對應關系見表1。

表1　Askey法則不同概率分布對應的正交多項式Tab.1 The correspondent Askey orthogonal polynomial chaos with different probability distribution

在進行實際的數值計算時，需要對多項式混沌展開式進行截斷

M取決于隨機變量的維數N和正交多項式基底的最高階數P。M可以通過下式進行計算

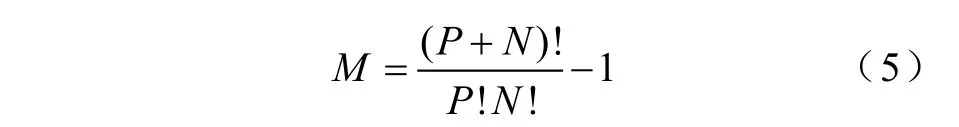
在實際系統中，往往包含多個不確定性參數，因此，基本的單變量、一維gPC無法解決多個不確定參數共同影響下系統的響應問題，因此，本文采用張量積的方法將一維的gPC擴展到多維。

在包含多個概率密度函數相同的隨機參數的系統中，隨機變量的維數N＞1，將一維的正交多項式表示為，通過將一維的正交多項式張量化構建多維的多項式混沌

定義N個隨機參數的索引，k＝{k1,…,k1,…,kN}，從而得到

在系統存在多個不確定性參數的情況下，利用構建的多維gPC基底，可以將系統中的各個狀態表示成式（1）所示的形式，結合Galerkin映射，根據正交性關系式（2）可以求得多項式混沌展開式的系數，在得到系數之后，通過處理便可以得到系統響應的各階矩，包括均值和方差，可以表示為

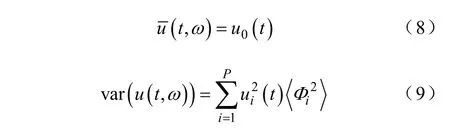
通過張量積的構建。可以將一維的多項式混沌擴展到多維，可以實現對包含多個不確定參數的系統的仿真不確定性分析。

2 多維gPC有效性驗證

為了對構建的多維gPC進行驗證，將其應用到一階隨機微分方程的求解中。考慮一階隨機微分方程

隨機微分方程解的均值和方差可以通過下式進行計算

采用多項式混沌對微分方程中的隨機變量進行展開，由表可知，均勻分布的隨機變量對應的最優多項式為Legendre多項式。一維Legendre多項式的三項遞推公式可以表示為

其權函數可以表示為

由于系統包含兩個隨機參數，根據多維gPC的構建方法，二維的Legendre多項式基底可以表示為

為表示方便，省略上標。隨機變量C可以表示為

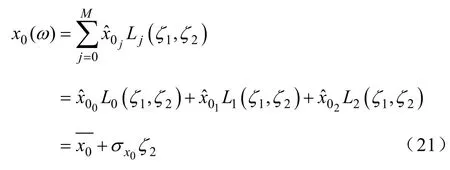
利用Galerkin映射可以將隨機的微分方程轉化成確定的微分方程，有，使得任意φ（ζ）∈VΓ和則

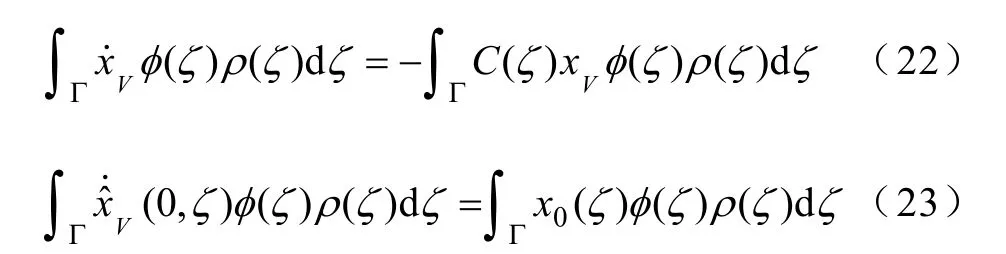
將多項式混沌展開式代入式（22）和式（23），根據多項式混沌的正交性，經整理之后可以得到

式中，k＝0,…,M；x?k為多項式混沌的模式；和分別為Legendre多項式的二重和三重內積，可以通過在已知區間內的二重積分求得。

在完成數值積分后，可以根據式（8）和式（9）通過得到的多項式混沌的系數重構隨機微分方程解的統計特性，隨機微分方程解的均值和方差可以表示為

圖1　P＝3時得到的不確定性仿真結果Fig.1 Solution of the uncertainty simulation when P＝3

圖2　P＝1～3時解的方差同解析解的比較Fig.2 Variations compared to the analytic solution when P＝1 to 3

圖1給出了N＝2、P＝3時求得的多項式混沌的模式，其個數滿足式（5）的關系，隨著P的增加，其個數將按照指數的趨勢增加。圖2給出了P＝1～3時，不確定性仿真得到的解的方差同解析解的比較，其中“ref”代表解析解得到的結果。可以看出，隨著P的增加，通過不確定性仿真得到的方差曲線逐漸向解析解的方差曲線靠近，在P＝3時，兩者基本吻合，這說明隨著多項式混沌階數P的增大，不確定性仿真的準確度也越來越高，但需要求解的ODE的個數也將大大增加，通過多維gPC在一階隨機微分方程求解中的應用證明了該方法在求解包含多個不確定性參數的系統中的有效性。

3 船舶電力推進系統仿真不確定性分析

為了使用gPC對船舶電力推進系統進行不確定性的仿真，首先需要進行系統的建模，并將模型表示為ODE的形式。本文研究的船舶電力推進系統結構如圖3所示[16]，其中包括了PWM電壓源逆變器（PWM-VSI）、直接轉矩控制（Direct Torque Control,DTC）、感應推進電機以及船槳負載。

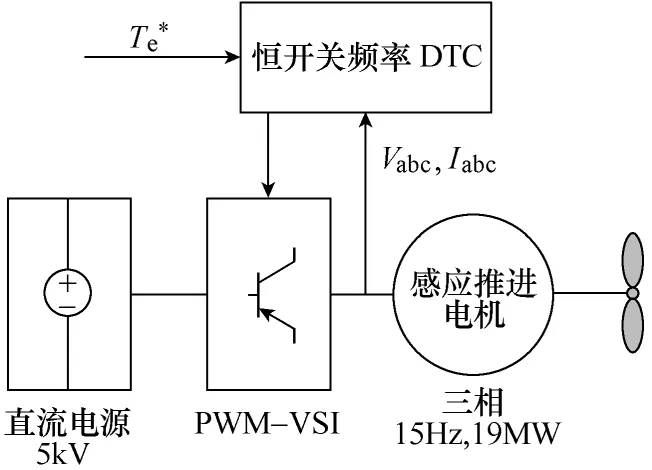
圖3　船舶電力推進系統結構示意圖Fig.3 Structure of the ship electric propulsion system

感應推進電機的模型建立在定子磁鏈參考坐標系下，PWM-VSI采用平均值模型[17]，輸入的PWM脈沖可以使用正弦電壓信號進行平均，表示為“mdqs”，感應推進電機的轉矩控制采用了恒開關頻率DTC方法[18]，使用兩個PI控制器分別調節感應推進電機的轉矩和磁鏈。螺旋槳的推力系數和轉矩系數以及船舶的航行阻力等擬合成表達式的形式，系統的輸入包括直流母線電壓、DTC系統中感應推進電機的電磁轉矩給定和定子磁鏈給定，船槳負載的輸入為感應推進電機的轉速，輸出為感應推進電機的負載轉矩。系統各部分包含的狀態變量以及輸入、輸出關系如圖4所示。

圖4　船舶電力推進系統各狀態變量與連接關系示意圖Fig.4 State variables and connections of the ship electric propulsion system

經過推導，得到系統的七階ODE模型為

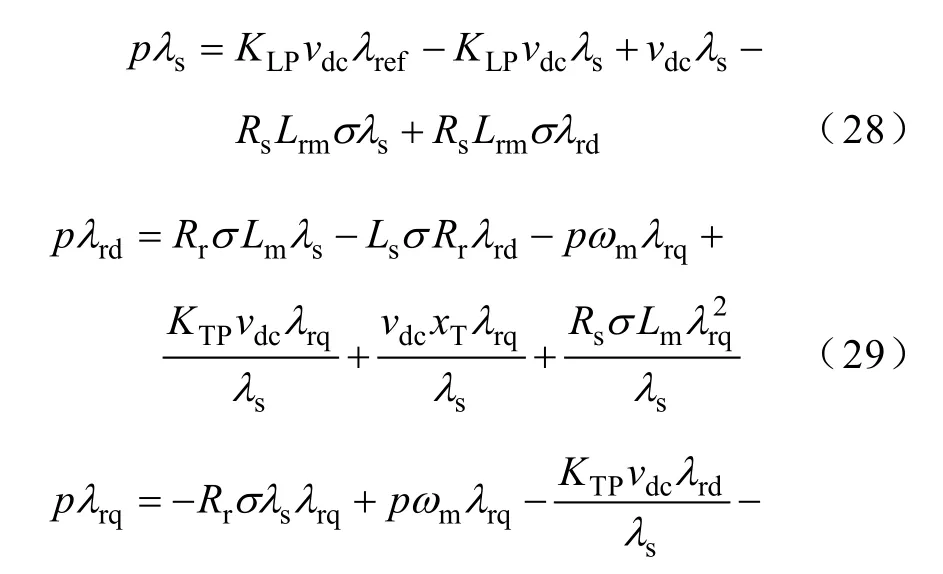
式中

式中，λs、λrd、λrq和ωm分別為感應推進電機的定子磁鏈、轉子d軸和q軸磁鏈以及轉速；xT，xλ為DTC控制中轉矩控制和磁鏈控制引入的內部狀態變量；vs為船舶的航速；KLP、KLI、KTP和KTI分別為轉矩控制器和磁鏈控制器的PI參數；J為轉動慣量；p為感應推進電機的極對數；KT和KQ分別為螺旋槳的推力系數和轉矩系數；td為推力減額系數；ρ為海水的密度；D為螺旋槳的直徑；Fr為船舶的航行阻力；m和ma分別為船舶的質量和附加質量。

船舶電力推進系統中的推進電機為三相、19MW的感應電動機，系統各部分的參數如下[19]。

（1）感應推進電機參數

Rs＝27m?，Rr＝8m?，fb＝15Hz，Lls＝1.5mH，Llr＝1.7mH，Lm＝31.7mH，p＝6。

（2）船槳負載參數

D＝5.5m，ρ＝1 025kg/m3，m＝1.327×107kg，ma＝1.08。

隨機海浪的擾動以及溫度等環境的變化將直接對系統的參數產生影響。首先，感應推進電機的轉子電阻受到溫度的影響非常嚴重，其最大的變化范圍可以達到其原始測量值的100%[20]；其次，船舶電力推進系統的推進電機和螺旋槳同軸相連，其轉動慣量由感應推進電機的轉動慣量和螺旋槳的轉動慣量兩方面構成，隨機海浪的擾動會給螺旋槳的旋轉帶來附加的轉動慣量，約在其原始值的0.3倍左右[21,22]，本文假設感應推進電機的轉子繞組Rr在其平均值的±30%范圍內均勻分布，轉動慣量J在其平均值的±40%范圍內均勻分布，由于溫度和海浪的隨機干擾沒有關聯，使得轉子繞組電阻和轉動慣量相互獨立。

仿真的工況為在初始時刻時以20kN·m/s的速度給定磁轉矩，在50s時給定電磁轉矩達到1 000kN·m時保持穩定，仿真共200s，不確定性仿真的多項式混沌階數P＝7，則經過二維Legendre多項式混沌展開之后，系統將包含252個ODE，通過數值積分算法對252個ODE進行數值積分求解，求解完成后對數值解進行重構可以得到各狀態變量以及輸出的均值與方差，仿真結果如圖5～圖9所示。

圖5　電磁轉矩仿真結果Fig.5 Simulation result of the electromagnetic torque

圖6　定子磁鏈仿真結果統計特性Fig.6 Simulation results of the stator flux

圖7　感應推進電機轉速仿真結果統計特性Fig.7 Simulation results of the motor rotational speed

圖8　船舶航速仿真結果Fig.8 Simulation results of the ship speed

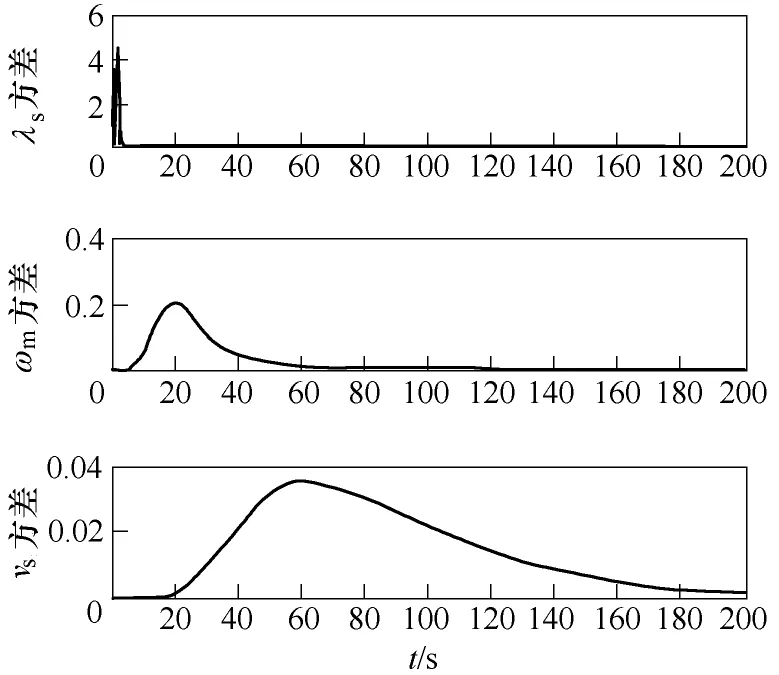
圖9　船舶航速仿真結果Fig.9 Simulation results of the ship speed

圖5給出了電磁轉矩的仿真結果曲線，可以看出，電磁轉矩跟隨給定值，從0時刻以20kN·m/s的速度增加，到50s時達到1 000kN·m并保持穩定。圖6分別給出了定子磁鏈仿真結果統計特性的全過程和局部曲線，圖7和圖8給出了感應推進電機和船舶航速仿真結果的統計特性曲線，包括了均值、以及均值加減標準差。可以看出，由于磁鏈控制器的作用，定子磁鏈迅速達到穩定，在電磁轉矩的上升階段，電動機的轉速迅速上升，當電磁轉矩達到并保持穩定之后，電動機轉速增幅變小，逐漸趨于穩定；船舶的航速由于慣性時間常數較大，在經過了一段快速上升的過程后逐漸趨于穩定。從統計特性可以看出，兩個不確定性參數對狀態變量的動態過程和穩態過程都將產生影響，其中動態過程中影響較大，進入穩態后影響較小。圖9給出了仿真全過程中電動機定子磁鏈、轉速和船舶航速的方差曲線，通過方差曲線可以看出，狀態變量的動態過程中方差較大，進入穩態后逐漸減小，這也與圖6～圖8得到的結果吻合；還可以看出，方差在從動態過程即將進入穩態時將出現一個最大值，此時，系統隨機響應在平均值上下的波動將最為嚴重，不確定性的參數對系統的影響也最為嚴重，得到的定量的不確定性分析結果能夠為系統的設計研發提供參考。

4 結論

在設計研發階段，由于船舶電力推進系統所面臨的不確定性因素較多，利用傳統的仿真不確定性分析手段將會使得整個設計研發過程效率低。本文在傳統的一維gPC的基礎上，利用張量積構建了多維的gPC，通過其在一維隨機微分方程中的應用提出了利用構建的多維gPC進行多個不確定性因素共同影響下不確定性分析的方法和流程，并驗證了方法的有效性。基于該方法進行了船舶電力推進系統的動態仿真不確性分析，得到的結果能夠直接應用到船舶電力推進系統的設計研發中，解決系統受不確定性因素影響較多的問題。

參考文獻

[1]Young S,Newell J,Little G.Beyond electric ship[J].Naval Engineers Journal,2001,113（4）:79-92.

[2]王淼,戴劍鋒,周雙喜,等.全電力推進船舶電力系統的數字仿真[J].電工技術學報,2006,21（4）:130-137.Wang Miao,Dai Jianfeng,Zhou Shuangxi,et al.Digital simulation of ship power system with electric propulsion[J].Transactions of China Electrotechnical Society,2006,21（4）:130-137.

[3]劉勝,張玉廷,余晨光.船舶電力推進系統電機組三維模糊控制[J].中國電機工程學報,2012,32（3）:117-123.Liu Sheng,Zhang Yuting,Yu Chenguang.Threedimensional fuzzy control for ship electric propulsion turbine[J].Proceedings of the CSEE,2012,32（3）:117-123.

[4]Krause P C,Wasynczuk O,Sudhoff S D.Analysis of electric machinery and drive systems,second edition[M].New York:IEEE Press and Wiley-Interscience,2002.

[5]董雷,楊以涵,張傳成,等.綜合考慮網絡結構不確定性的概率潮流計算方法[J].電工技術學報,2012,27（1）:210-216.Dong Lei,Yang Yihan,Zhang Chuancheng,et al.Probabilistic load flow considering network configuration uncertainties[J].Transactions of China Electrotechnical Society,2012,27（1）:210-216.

[6]段玉兵,龔宇雷,譚興國,等.基于蒙特卡羅模擬的微電網隨機潮流計算方法[J].電工技術學報,2011,26（1）:274-278.Duan Yubing,Gong Yulei,Tan Xingguo,et a1.Probabilistic power flow calculation in microgrid based on Monte-Carlo simulation[J].Transactions of China Electrotechnical Society,2011,26（1）:274-278.

[7]趙淵,沈智健,周念成,等.大電網可靠性蒙特卡洛仿真的概率不確定性分析[J].中國電機工程學報,2008,28（28）:61-67.Zhao Yuan,Shen Zhijian,Zhou Niancheng,et al.Probabilistic uncertainty analysis of Monte-Carlo simulation for bulk power system reliability evaluation[J].Proceedings of the CSEE,2008,28（28）:61-67.

[8]Fishman G S.Monte Carlo:concepts,algorithms,and applications[M].New York:Springer-Verlag Inc,1996.

[9]Ghanem R G,Spanos P D.Stochastic finite elements:a spectral approach,revised edition[M].USA:Dover Publications,2003.

[10]Xiu D,Karniadakis G E.The Wiener-Askey polynomial chaos for stochastic differential equations[J].SIAM Journal on Scientific Computing,2002,24（2）:619-644.

[11]Xiu D,Karniadakis G E.Modeling uncertainty in flow simulations via generalized polynomial chaos[J].Journal of Computation Physics,2003,187（1）:137-167.[12]Hover F S,Triantafyllou M S.Application of polynomial chaos in stability and control[J].Automatica,2006,42（5）:789-795.

[13]Lovett T E,Monti A,Ponci F.Automatic synthesis of uncertain models for linear circuit simulation:a polynomial chaos theory approach[J].Simulation Modelling Practice and Theory,2008,16（7）:796-816.

[14]王曉東,康順.多項式混沌方法在隨機方腔流動模擬中的應用[J].中國科學E輯:技術科學,2011,41（6）:790-798.Wang Xiaodong,Kang Shun.Application of polynomial chaos on numerical simulation of stochastic cavity flow[J].Science China Technological Sciences,2011,41（6）:790-798.

[15]韓冬,馬進,賀仁睦,等.基于隨機響應面法的電力系統仿真不確定性分析[J].電力系統自動化,2011,35（24）:l2-16.Han Dong,Ma Jin,He Renmu,et a1.Uncertainty analysis based on stochastic response surface method in power system simulaton[J].Automation of Electric Power Systems,2011,35（24）:l2-16.

[16]Bash M,Chan R R,Crider J,et al.A medium voltage DC testbed for ship power system research[C]//Electric Ship Technologies Symposium,2009:560-567.

[17]Rim C T,Choi N S,Cho G C,et al.A complete DC and AC analysis of three-phase controlled-current PWM rectifier using circuit DQ transformation[J].IEEE Transactions on Power Electronics,1994,9（4）:390-396.

[18]Xue Y,Xu X,Habetler T G,et al.A low cost stator flux oriented voltage source variable speed drive[C]//Conference Record of the IEEE Industry Applications Society Annual Meeting,1990:410-415.

[19]Marden M M,Prempraneerach P,Kirtley J L,et al.An end-to-end simulator for the all-electric ship MVDC integrated power system[C]//Proceedings of the 2010 Conference on Grand Challenges in Modeling＆ Simulation,Society for Modeling ＆ Simulation International,2010:136-143.

[20]Francois B,Degobert P,Hautier J P.Vector control of induction machines:desensitisation and optimisation through fuzzy logic[M].Springer,2012.

[21]孫洪波.螺旋槳逆轉工況下船舶運動建模與仿真[D].大連:大連海事大學,2007.

[22]Prempraneerach P,Kirtley J,Chryssostomidis C,et al.Stochastic modeling of integrated power system coupled to hydrodynamics in the all-electric ship[C]//IEEE International Symposium on Power Electronics,Electrical Drives,Automation and Motion,2008:563-568.

劉 勝 男，1957年生，教授，博士生導師，研究方向為隨機系統最優估計與控制、船舶電力推進和復雜性科學等。

E-mail:cyz410410@163.com

程垠鐘 男，1987年生，博士研究生，研究方向為船舶綜合電力推進系統的建模與仿真。

E-mail:cyzelvis@163.com（通信作者）

Uncertainty Analysis for Simulation of Shipboard Electric Propulsion System Based on Multi-Dimensional gPC

Liu Sheng Cheng Yinzhong
（College of Automation Harbin Engineering University Harbin 150001 China）

AbstractIn order to analyze the influence of many uncertain factors on the design stage of shipboard electric propulsion systems,gPC was applied in the uncertainty analysis of system simulation.A method to construct multi-dimensional gPC from one-dimension gPC by tensor product was adopted in this paper.By applying the method in the first-order stochastic differential equation,the efficiency of the proposed method was validated.Then,uncertainty analysis of the simulation for the shipboard electric propulsion systems arising from two independent random variables was analyzed.The statistical properties of variables were obtained.The results showed that the proposed method can simulate and analyze the performance of the shipboard electric propulsion system affected by multiple uncertain factors effectively.The dynamic and steady-state performance of the system will be affected by the random variables.The largest impact appears when the system is about to steady-state from dynamic process,which can provide reference for design and development.

Keywords：Shipboard electric propulsion,simulation,uncertainty analysis,generalized polynomial chaos

作者簡介

收稿日期2013-10-22 改稿日期 2013-12-05

中圖分類號：TM743