引他山之石 攻生物之玉

商爽

摘 要：在生物學的教學中，引導學生將數學、物理、化學等學科思維方法進行遷移，來構建生物學模型，可以使學生對學科知識與建模方法融會貫通，也增加了學生對模型構建的興趣，提高了學生用已有知識方法創新的能力。

關鍵詞：跨學科；思維方法；模型構建

模型構建是一種學習包括生物學在內的自然科學的重要方法。高中學生在學習生物學之前已具備了一定的數學、物理、化學等方面的思維方法與模型構建能力。在生物學的教學中，可采他山之石為我所用，引導學生將其他學科的思維方法進行遷移來構建生物學模型。這樣不僅可以使學生對學科知識與建模方法融會貫通，也增加了學生對模型構建的興趣，提高了學生用已有知識方法創新的能力。本文結合筆者在教學中應用的三個實例談談具體應用的策略與體會。

一、從化學中的反應平衡到生物學中體溫調節模型的構建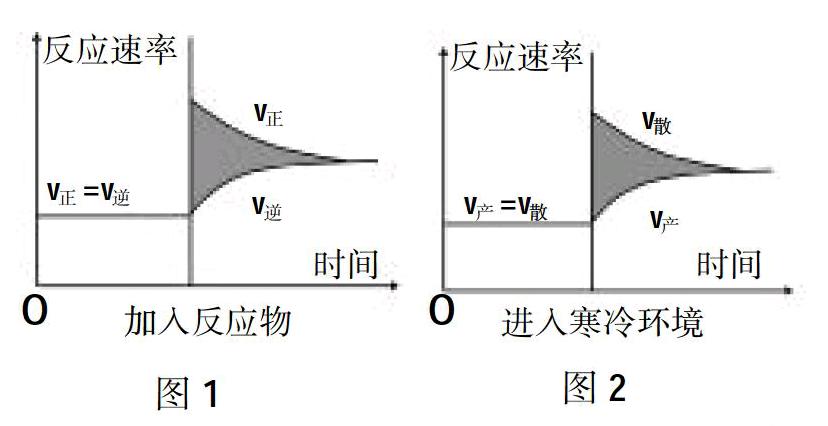

人體體溫調節是高中生物學教學中的難點。以人體從溫暖環境進入寒冷環境為例，學生對“機體會增加產熱，減少散熱，但產熱速率與散熱速率均增加”這一內容往往難以理解，一些學生只能采取死記硬背、不斷重復記憶的低效率學習方法。構建一個體溫調節的模型，讓學生能更好地理解體溫調節的機理與變化，將讓教學變得更有效。

高中學生在化學學習中曾構建過化學反應平衡模型，加入反應物后的化學反應平衡變化如圖1所示。反應平衡時，正逆反應速率相等，即v正=v逆，此時若向平衡體系中加入正反應的反應物，則v正會迅速上升，而v逆也由于逆反應底物增多而加快，最終達到新的平衡，v正=v逆且均上升，而圖中灰色區域可理解為正反應生成物的增多量。教師可以以此為思維出發點，在體溫調節的教學過程中讓學生來建立類似模型，引導學生把反應平衡中正逆反應速率替換為體溫調節中的產熱速率（v產）與散熱速率（v散），在同樣的坐標系中畫出人體從溫暖環境進入寒冷環境的v產與v散變化模型。由于反應平衡模型是學生較為熟悉的模型，學生通過類比就較容易畫出圖2，結合圖2就能較好地理解人體進入寒冷環境后的體溫調節的變化：由于機體與外界的溫差加大使機體的v散迅速上升，機體為了維持體溫平衡，做出了減少v散、增加v產的各種調節活動，但最終v產與v散均上升，而圖中的灰色區域可理解為體表或肢端熱量散失（體表或肢端溫度下降）。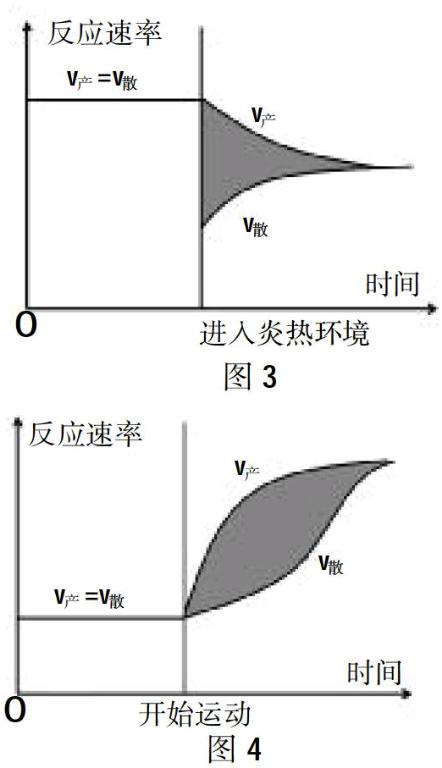

依照上述模型，我們還可以在教學中讓學生進一步自主構建人體進入炎熱環境后的體溫調節模型（如圖3）和人體開始進行劇烈運動的體溫調節模型（如圖4）。

二、從物理學中的“受力分析”到生物學中能量流動分析模型的構建

構建模型化平衡體系的思維方法不只存在于化學學科中，物理學中的受力分析是另一個很好的實例。高中學生都知曉，當物體所受合力為0時，將保持靜止或是勻速運動狀態（平衡狀態），在所受合力不為0時，其運動狀態會發生改變，如發生加速或減速運動。所以，物理學中研究物體運動狀態時，必須先構建受力分析模型，找出物體所受的各種力，再計算物體所受合力，根據合力來推測物體所處運動狀態；反之也可以根據已知的運動狀態來分析物體的受力情況。

這種“從散到全，從靜到動”的思維方法同樣也可以遷移到生物學的教學中，在研究生態系統能量流動及發展變化時，可將生態系統的發展情況比作物體的運動狀況，則能量的流動就相當于物體的受力狀況。學生通過分析能量流入與流出生態系統的情況，得出“對一個生態系統而言，其流入生態系統的能量主要是總初級生產量（GP）和人工補充量（S），而流出生態系統的能量主要是各生物成分的呼吸總量（R）”，根據平衡變化原理，有：

①GP+S﹥R，生態系統處于發展或恢復階段；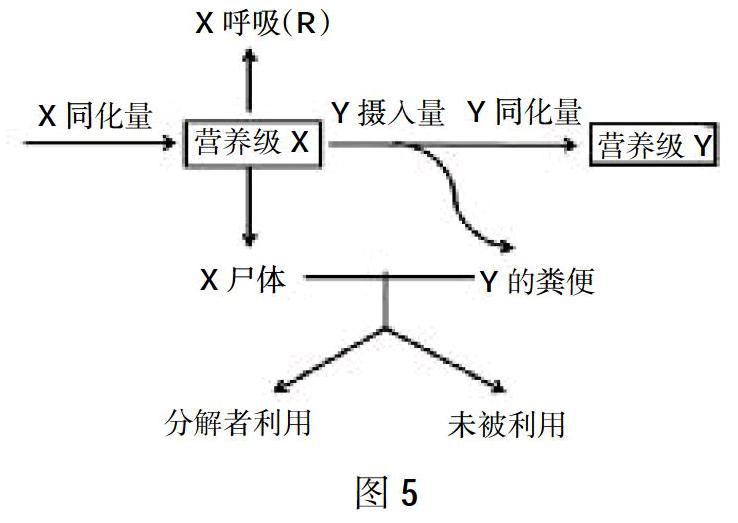

②GP+S=R，生態系統處于平衡狀態；

③GP+S﹤R，生態系統處于衰退階段。

同樣，教師還可以引導學生構建一個營養級模型，如X營養級能量分析模型。學生不難發現，與“分析受力情況是弄清物體運動狀況的前提”一樣，要推測X營養級能量情況及未來動態變化，就必須分析能量流入與流出該營養級的所有方式，再計算比較總流入量與總流出量才能得出結論。學生通過自主分析和相互討論可知“流入X營養級的能量為它的同化量，而流出X營養級的能量包括X自身的呼吸、被下一營養級捕食（包含被下一營養級同化的量和糞便量）以及被分解者利用和未被利用的幾個部分構成” ，在此基礎上構建了如圖5的分析模型。

那么，“一個成熟穩定的生態系統中的X營養級應滿足什么樣的條件”，“X營養級所含能量（或生物量）未來會增加的前提條件是什么”， “能量傳遞效率的分析與計算”等問題都可以讓學生在上述模型基礎上進行探討分析。

三、從數學的乘法分配律到基因自由組合規律的計算模型構建

筆者在教學中發現，學生在利用概率演算來解決兩對相對性狀遺傳問題時往往出現推理慢且對一些細節考慮不全面的問題。例如下題：

將兩不同表現型的豌豆相互雜交，F1中黃色（Y）圓形∶（R）黃色皺形∶綠色圓形∶綠色皺形=1∶1∶1∶1，則親本豌豆的基因型分別為。

由于1∶1∶1∶1是兩對相對性狀測交實驗的比例，本題學生比較容易想到的答案是YyRr×yyrr，但本題的另一種答案Yyrr×yyRr卻往往被學生所忽略。主要原因是學生常以經驗去解決這一問題，而沒有逐對性狀去考慮。其實，自由組合規律無非是兩個相對獨立事件的總和，那么1∶1∶1∶1的比例實際上是兩對性狀各自出現（1∶1）的結果，也即1∶1∶1∶1可等價于（1∶1）（1∶1）。對此，學生很快能聯想到數學中的乘法分配率：

（a+b）（c+d）=ac+ad+bc+bd，

并從中變化：

（a∶b） （c∶d ）=ac∶ad∶bc∶bd。

上述模型并不嚴格符合數學邏輯，但卻很好地解釋了兩獨立事件比例乘積即是總比例的概率思維，也是解決自由組合規律問題“先分后合”的思維體現。按此模型，學生可以做以下一些推論：

①孟德爾兩對相對性狀實驗中F1自交比例：9∶3∶3∶1等價于（3∶1）（3∶1）；

②一對性狀存在顯性純合體致死的情況下的F1自交比例：6∶3∶2∶1等價于（3∶1）（2∶1）；

③兩對性狀均存在顯性純合體致死的情況下F1自交比例：4∶2∶2∶1等價于（2∶1）（2∶1）；

④一對性狀為不完全顯性情況下F1自交比例：3∶6∶3∶1∶2∶1等價于（3∶1）（1∶2∶1）；

……

這些推論可以幫助學生更快更全面地解決一些遺傳學問題。

教師的教學必須尊重學生已有的知識與思維方法。利用學生已具備的數理化學科思維來引導學生構建生物學模型比傳統的構建方法更有效，也更能激發學生學習的積極性。隨著教學進度的推進，也可以進一步讓學生根據自身具有的數理化學科思維進行完全自主的模型構建與探討。