基于CEEMD和奇異值差分譜的滾動軸承故障特征提取

張會敏，唐貴基（華北電力大學能源動力與機械工程學院，河北保定071003）

?

基于CEEMD和奇異值差分譜的滾動軸承故障特征提取

張會敏，唐貴基
（華北電力大學能源動力與機械工程學院，河北保定071003）

摘要：針對滾動軸承故障信號非線性、非平穩特征導致的故障頻率難以提取的問題，提出一種基于補充總體平均經驗模態分解（Complementary EEMD，CEEMD）和奇異值差分譜結合的滾動軸承故障診斷方法。CEEMD分解向原信號成對地添加符號相反的白噪聲，幾乎消除殘留白噪聲的影響。首先，對故障信號利用CEEMD算法進行分解，得到若干IMF（Intrinsic Mode Function）分量，然后運用相關系數—峭度準則對IMF分量進行篩選并重構，再對重構信號進行奇異值分解，并求出奇異值差分譜，根據奇異值差分譜理論進行消噪和重構，最后對重構信號進行Hilbert包絡譜分析，提取故障頻率。實驗結果表明，提出的方法，能精確地提取滾動軸承的故障頻率。

關鍵詞：CEEMD；奇異值差分譜；相關系數—峭度準則；滾動軸承；故障診斷

0 引言

滾動軸承在機械設備中應用廣泛，且其工作情況的好壞對機器的運轉影響很大。其故障輕則導致機械設備產生異常振動和噪聲，重則造成設備損壞和人員傷亡［1，2］。所以，對滾動軸承進行故障診斷極其重要。

Huang［3］等提出了經驗模態分解（EMD），這是一種自適應信號處理方法，該方法提出以后得到了廣泛的應用［4－6］。但其也存在一些問題，主要是模態混疊。因此，文獻［6］提出了總體平均經驗模態分解（EEMD），該方法首先向原信號添加白噪聲，之后進行EMD分解，EEMD方法在一定程度上抑制了EMD分解所產生的模態混疊問題，顯著提高了EMD算法的穩定性，但由于添加的白噪聲不能完全被中和，會有部分白噪聲殘留在IMF的分量當中，從而得不到純凈的IMF分量。

補充的總體平均經驗模態分解（CEEMD）通過向原信號中成對添加符號相反的白噪聲，然后分別對添加正負白噪聲的兩組信號進行EMD分解。CEEMD方法不僅有效解決了EMD分解的模態混疊的問題，并且幾乎消除了殘留白噪聲的影響。本文在對原始信號做完CEEMD分解之后，運用相關系數—峭度準則對IMF分量進行選擇，并將符合條件的分量進行重構。由于故障信號中有背景噪聲，故障頻率往往被淹沒在背景噪聲中。為了能更加準確的提取故障頻率，進一步使用差分譜理論對得到的重構信號進行消噪處理。

基于此，本文提出了基于補充總體經驗模式分解（CEEMD）和奇異差分譜理論的軸承故障特征提取方法。通過仿真信號及實驗數據的驗證，該方法能夠有效地應用于軸承故障特征提取。

1 CEEMD理論

設原始信號為x（t），EMD算法將x（t）分解為一組IMF分量Ci和余項rn的和，即

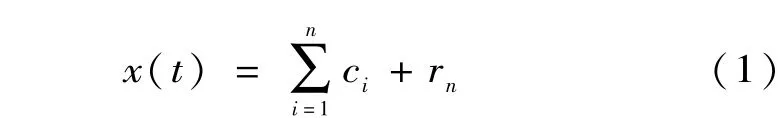
EEMD是通過向原信號添加白噪聲后再進行EMD分解，最終取各個IMF分量的均值作為最后的結果。為了避免EEMD添加的白噪聲不能完全被中和以及運算時間過長的問題，CEEMD算法中，在原信號中成對地添加正負兩組白噪聲，然后分別對兩組加噪信號進行EMD分解，所以最終的IMF分量是由殘留正白噪聲和負白噪聲的兩組IMF分量求平均得到。Yeh［7，8］等提出CEEMD分解步驟如下：

（1）在原始信號中加入白噪聲序列n1（t）。

（2）把加噪數據分解到IMF中，得到第一組內稟模態函數c1i，r1。

（3）在目標數據中加入與第一步符號相反的白噪聲序列－n1（t）。

（4）將含噪數據分解到IMF中，得到第二組內稟模態函數c－1i，r－1。

（5）并重復執行（1）～（4），得到n組cni，rn，c－ni，r－n。

（6）得到殘留正白噪聲和負白噪聲的兩組IMF分量，求兩組分量均值并得到最終IMF。 n

在CEEMD分解的過程中需要確定兩個參數：所添加的高斯白噪聲的幅值ε及CEEMD分解的次數N。在EEMD分解中添加白噪聲殘余量應滿足以下公式，εn＝ε／N，其中N為集成次數，ε是添加噪聲的幅值，εn為原信號與各分量重構信號的誤差的標準差。添加白噪聲的幅值過小或者集成次數過少，起不到改變極值點的分布的作用，從而不能均勻極值點分布；如果幅值太大或者集成次數太多，雖然能夠減少添加白噪聲的影響，但會增加運行時間［5］。文獻［6］建議：添加白噪聲的幅值為原信號的標準差（Standard Deviation，SD）的0. 1～0. 2。

為了證明該方法的有效性，用以下仿真信號進行驗證：

對x（t）分別進行EEMD、CEEMD分解。其中EEMD算法中所添加的噪聲幅值為0. 2，添加噪聲個數150個。CEEMD添加噪聲75對（為EEMD添加噪聲個數的一半），添加噪聲幅值也為0. 2。其分解結果分別如圖2和圖3所示。

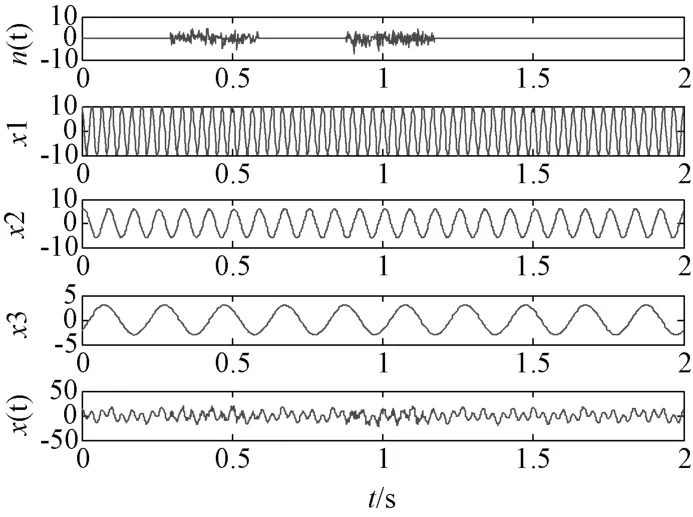
圖1　仿真信號及各組成成分的時域波形

EEMD的分解結果如圖2所示，IMF1為一定程度上受到添加白噪聲污染的間歇隨機信號，IMF2?4為組成原始仿真信號的三個正弦信號，通過添加白噪聲，并經過一定次數的集成平均，一定程度上抑制了了EMD分解的模態混淆，但是明顯看出仍然存在模態混疊，添加的白噪聲并沒有完全被中和。圖3為CEEMD分解結果，其中IMF2?4分別對應組成原始仿真信號的三個正弦信號x1（t）、x2（t）和x3（t），可以看出CEEMD分解基本消除了模態混疊的現象，由分解得到的間歇信號為零的部分可以看出，原信號所加白噪聲基本消除。并且經計算，CEEMD分解的殘余白噪聲已經不足0. 03%，噪聲中和的效果較好。且其他參數相同的情況下，CEEMD算法用時較短，大大提高了運算效率。

通過以上仿真信號可以初步證明，CEEMD方法對含噪信號有較好的分解效果，能夠更好地抑制模態混疊，對噪聲的中和效果更好，并提高了運算效率。

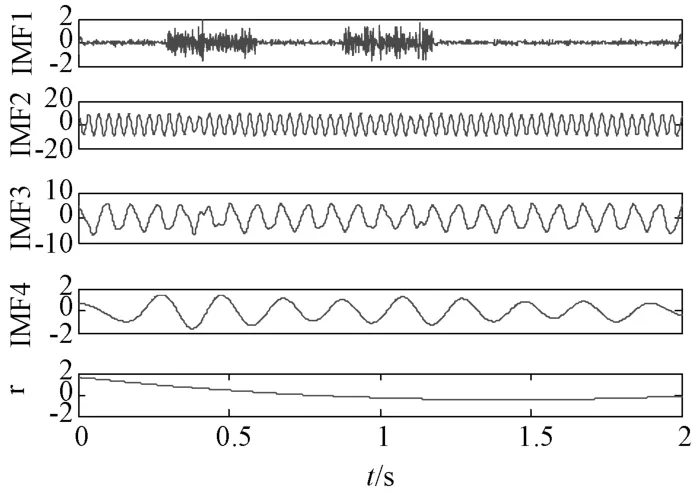
圖2　仿真信號的EEMD分解結果

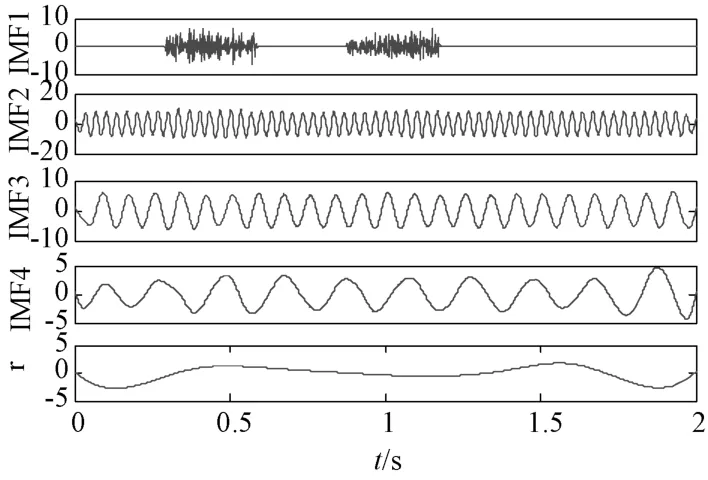
圖3　仿真信號的CEEMD分解結果

2 奇異值差分譜理論

奇異值分解技術在故障診斷中已經得到了成功應用，主要用于信號的降噪和周期性分量的提取。

設離散數字信號X＝［x（1），x（2），…，x（N）］，其奇異值差分譜的求解過程如下。構造Hankel矩陣如下：

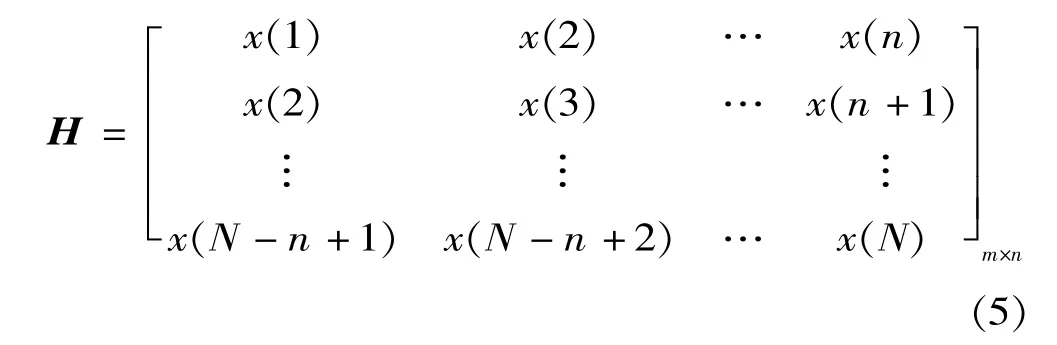
式中：1＜n＜N。令m＝N－n＋1，則H∈Rm×n，稱該矩陣為重構吸引子軌道矩陣［11，12］。

對上述吸引子軌道矩陣A∈Rm×n而言，不管它的行和列相關與否，一定會存在正交矩陣U＝（u1，u2…，um）和V＝（v1，v2…，vn）［12］，使得

式中：U∈Rm×m和V∈Rn×n分別表示左右奇異陣；S＝（diag（σ1，σ2，…，σq），0）或其轉置，這由m＜n還是m＞n來決定；其中，A∈Sm×n，0代表零矩陣；q＝min（m，n），σ1≥σ2≥…≥σq≥0，稱為矩陣A的奇異值。

從根本上來講，奇異值分解是將原信號分解為一系列分量信號的簡單線性疊加，并且相位偏移為零，故可選取若干分量進行疊加，從而實現對信號進行重構和降噪［9，10］。

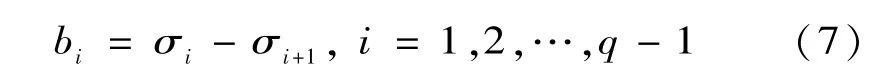
為了確定重構階數，提出差分譜［10］的概念，定義：則所有的bi形成的序列B＝［b1，b2，…，bq－1］稱為奇異值的差分譜序列，描述的是相鄰奇異值變化。在整個差分譜中必定存在一個最大的峰值bk。在軸承的故障診斷中，由故障引起的撞擊、振蕩或結構的斷裂往往是由最大突變點來反映［11］。奇異值之所以在最大突變點處產生的差異最大，是因為有用信號和噪聲的相關性差異造成的［1］。

有用信號包含在前面的k個奇異值對應的分量當中，而噪聲信號則包含在之后奇異值所對應的分量之中。可以根據奇異值差分譜最大峰值對應點的位置來決定重構階數。

為了驗證奇異值差分譜理論，取以下仿真信號進行驗證：

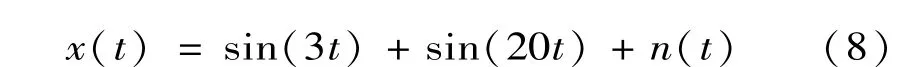
式中：n（t）為服從高斯分布的白噪聲，信噪比為1. 073 2，取樣區間為［0，2π］，取512個點。原信號如圖4所示。將原始信號x（t）＝sin（3t）＋sin（20t）＋n（t）構造Hankel矩陣，對其進行奇異值分解，并求得差分譜，如圖5所示，并將兩者得到的序列前50個點繪制在同一個坐標系中，可見，最大峰值發生在第4個點處。因此，重構階數為4，重構結果如圖6所示。其中虛線是原信號中不含噪聲的兩正弦信號的疊加。可見重構信號與理想幾乎重疊，并且沒有相位偏移，能夠有效消除噪聲。

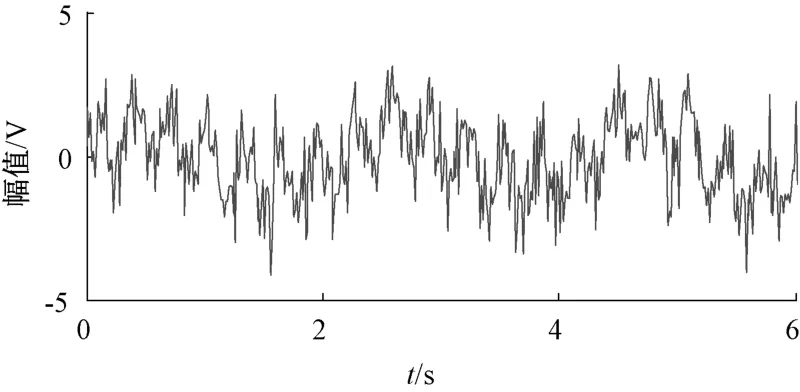
圖4　原始含噪信號

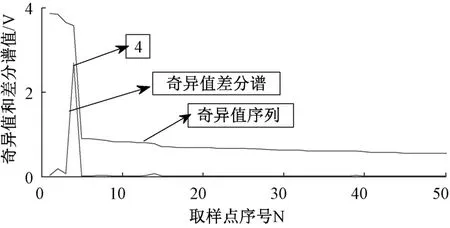
圖5　奇異值和奇異值差分譜的前40個點

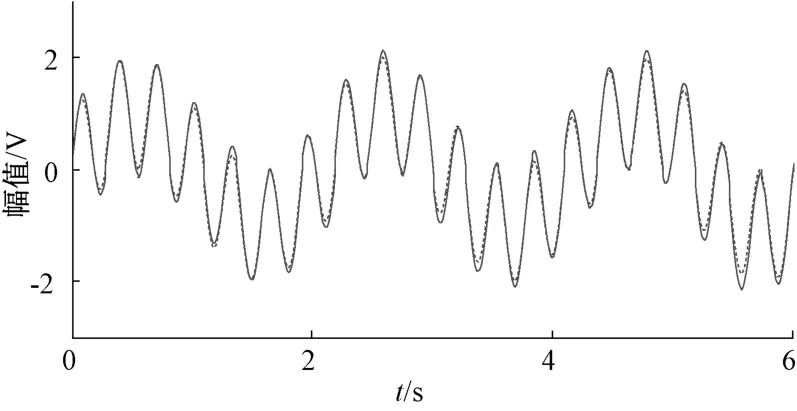
圖6　前4個分量的重構信號

將以上奇異值差分譜理論與CEEMD方法相結合，并應用到軸承故障診斷中，應能夠很好去除背景噪聲的影響，進而能夠更為準確無誤地提取故障特征。

3 滾動軸承故障診斷操作流程

該方法實現流程如圖7所示。

圖7　故障診斷流程

其具體的操作步驟如下：

（1）對原始信號做CEEMD運算，得到若干IMF分量。

（2）求取每個IMF分量和原信號相關系數，并保留相關系數大于閥值θ＝0. 1的分量，并對保留的分量求峭度值，選峭度較大的兩個IMF分量重構。

（3）對重構信號構建Hankel矩陣。

（4）對Hankel矩陣進行奇異值分解。

（5）求差分譜，并繪制差分譜序列圖。找出序列圖中最大峰值點，即重構階數。

（6）重構信號，并求其頻譜及希爾伯特包絡譜。

（7）從希爾伯特包絡譜中確定是否發生故障及故障部位。

4 實例應用與分析

實測信號為西儲大學滾動軸承內圈故障信號，采樣頻率為12 000 Hz，轉速N＝1 750 r／min，使用電火花加工技術在軸承上布置單點故障，故障直徑為0. 035 56 cm，通過計算可得軸承轉頻為29. 2 Hz，內圈故障特征頻率為157. 9 Hz。

圖8和圖9分別為軸承內圈故障的時域波形及頻譜。從時域圖中可以看到較為明顯的周期性沖擊，但是故障特征不明顯。在頻譜當中，亦存在較為明顯的邊頻帶以及很多共振頻率，因此僅通過時域波形和頻譜無法得到故障信息。求取故障信號的包絡譜，如圖10所示。可以顯示158. 2 Hz的故障頻率，但是也被埋藏在其他的頻率當中，不能確定就是內圈故障。利用CEEMD對信號進行分解，總體平均次數設為150次，添加噪聲幅值為0. 2。

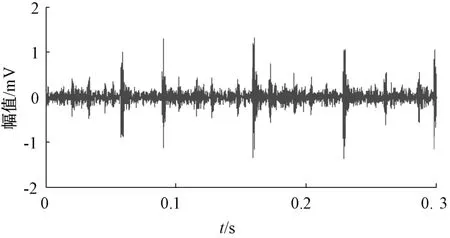
圖8　軸承內圈故障信號時域圖

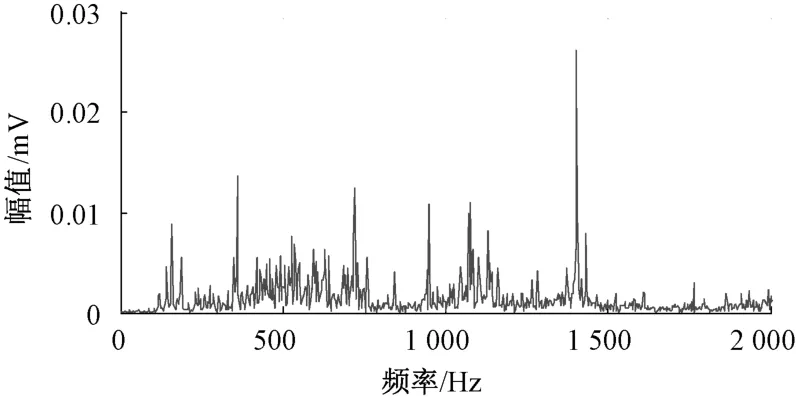
圖9　軸承內圈故障信號頻譜圖

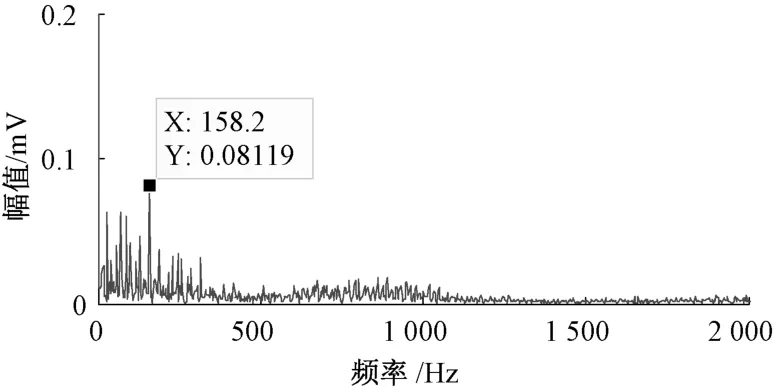
圖10　軸承內圈故障信號信號包絡譜

表1為CEEMD分解各個分量與原信號的相關系數，可以發現IMF1～IMF3與原信號的相關系數大于所設定的閥值，所以取前三個分量的峭度值中較大的兩個，如表2所示。可以看出前兩個分量的峭度值較大，所以選取前兩個分量進行重構。

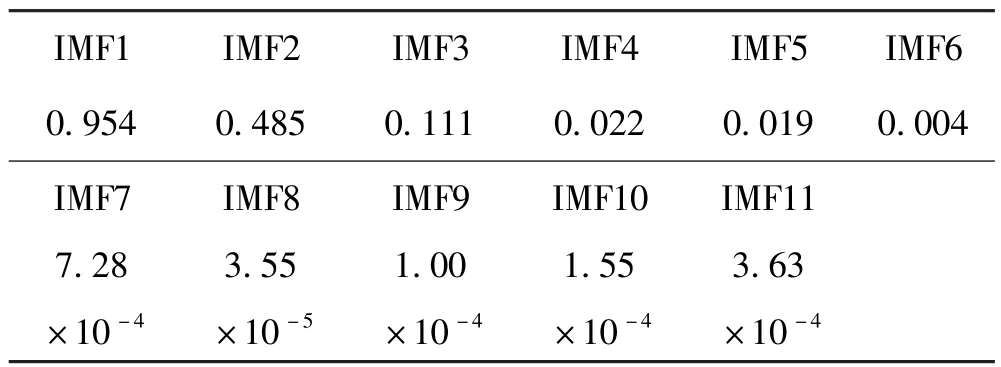
表1　各分量的相關系數

接下來對重構信號構造Hankel矩陣并做奇異值分解，并繪制奇異值差分譜圖，如圖11所示。

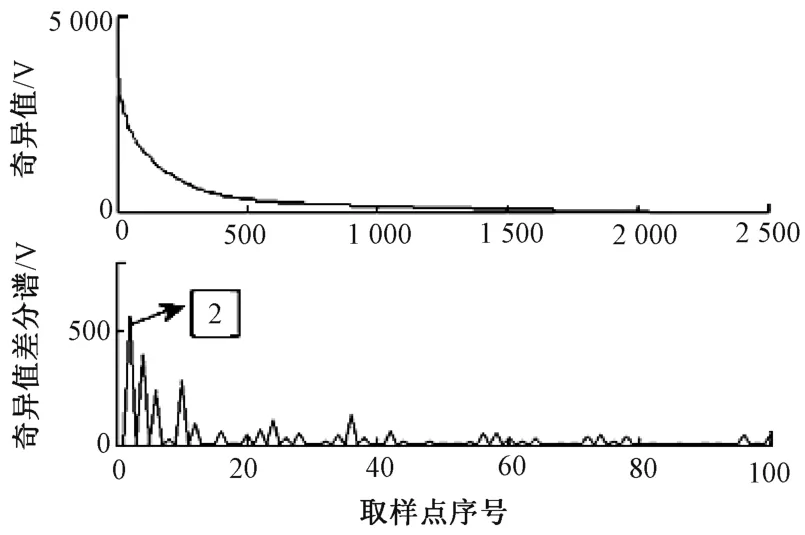
圖11　IMF1的奇異值和差分譜

由圖11可以確定譜圖中最大峰值點為2，即重構階數為2。所以取奇異值分解的前2個分量進行重構結果得到如圖12所示。與圖8相比，重構信號的幅值變小，且存在明顯的調幅信號，求取重構信號的包絡譜如圖13，其中29. 3 Hz為轉頻，158. 2 Hz近似等于內圈故障頻率，所以可以判斷軸承發生內圈故障。

表2　各分量的峭度值

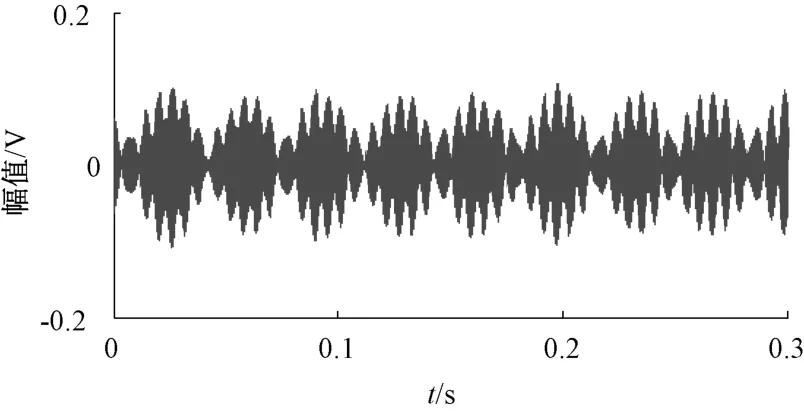
圖12　重構前10個分量后的信號

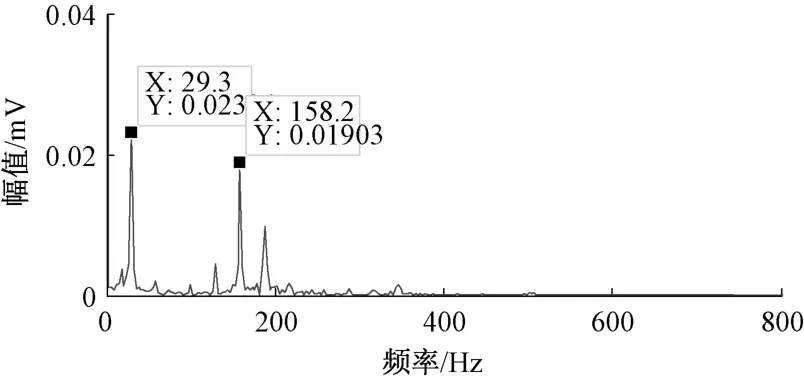
圖13　重構信號的包絡譜

5 結論

本文研究了CEEMD和奇異值差分譜理論結合的一種軸承故障特征提取方法。并得出以下結論：對比發現，CEEMD方法對所添加白噪聲的中和效果較好，很好的抑制了模態混疊，縮小了重構誤差，并且大大提高了運算效率；相關系數－峭度準則能有效篩選出用于重構信號的IMF分量；運用奇異值差分譜理論能夠很好的消除噪聲的影響；將CEEMD方法和奇異值差分譜理論結合進行故障診斷，能夠準確提取故障特征。

參考文獻：

［1］張超，陳建軍，徐亞蘭．基于EMD分解和奇異值差分譜理論的軸承故障診斷方法［J］．振動工程學報，2011，24（5）：539－545．

［2］湯寶平，蔣永華，張詳春．基于形態奇異值分解和經驗模態分解的滾動軸承故障特征提取方法［J］．機械工程學報，2010，46（5）：37－42．

［3］HUANG N E，SHEN Z，LONG S R，et al．The empirical mode decomposition and the Hilbert spectrum for nonlinear and non?stationary time series analysis［J］．Procedures of the Royal Society of London，SeriesA，1998，（454）：903－995．

［4］王曉龍．基于EEMD和Teager能量算子解調的故障診斷研究［J］．電力科學與工程，2013，29（3）：18－22．

［5］鄭近德，程軍圣，楊宇．改進的EEMD算法及其應用研究［J］．振動與沖擊，2013，32（21）：21－26．

［6］HUANG N E，WU Z．A review on Hilbert?Huang trans?form：Method and its applications to geophysical studies ［J］．Reviews of Geophysics，2008，46（2）：2008．

［7］YEH J R，SHIEH J S，NORDEN E，et al．Complemen?tary ensemble empirical mode decomposition：A noise en?hanced data analysis method［J］．Advances in Adaptive Data Analysis，2010，2（2）：135－156．

［8］唐貴基，王曉龍．基于EEMD降噪和1．5維能量譜的滾動軸承故障診斷研究［J］．振動與沖擊，2014，33 （1）：6－10．

［9］龐彬，唐貴基．基于滑動峭度法和Teager能量譜的滾動軸承故障診斷［J］．電力科學與工程，2014，30 （9）：25－29．

［10］蘇文勝，王奉濤，張志新，等．EMD降噪和譜峭度法在滾動軸承早期故障診斷中的應用［J］．振動與沖擊，2010，29（3）：18－21．

［11］呂志民，張武軍，徐金梧，等．基于奇異譜的降噪方法及其在故障診斷技術中的應用［J］．機械工程學報，1999，35（3）：85－88．

［12］趙學智，葉邦彥，陳統堅．奇異值差分譜理論及其在車床主軸箱故障診斷中的應用［J］．機械工程學報，2010，46（1）：100－108．

Feature Extraction of Rolling Bearing Fault Based on Ways of CEEMD and Difference Spectrum of Singular Value

ZHANG Huimin，TANG Guiji
（School of Energy Power and Mechanical Engineering，North China Electric Power University，Baoding 071003，China）

Abstract：Due to the non?stationary and non?linear characteristics of motor rolling bearings vibration signal which makes it hard to extract the fault frequency，a new method of fault diagnosis for the rolling bearings based on com?plementary ensemble empirical mode decomposition（CEEMD）method and difference spectrum of singular value is proposed．By adding the white noise in pairs into a target signal，the method of complementary EEMD（CEEMD）almost eliminates the influence of the white noise．Firstly，bearing fault signals are decomposed into a finite num?ber of IMFs based on the way of CEEMD；Then，filtering the components according to the correlation coefficientkurtosis criteria，and the selected IMF components are used to reconstruct the signal．A Hankel matrix is construc?ted by the reconstructed signal and the singular value difference spectrum can be obtained after singular value de?composition．Then，the singular value difference spectrum theory is used to reconstruct signal and eliminate noise．Finally，the reconstructed signal is demodulated by Hilbert transformation to extract the fault features．Results of experiment signals analysis show that the method proposed in this paper can identify gear fault patterns effectively．

Keywords：complementary ensemble empirical mode decomposition（CEEMD）；difference spectrum of singular value；correlation coefficient－kurtosis criteria；motor bearings；fault diagnosis

作者簡介：張會敏（1989－），女，碩士研究生，從事機械設備狀態監測與故障診斷方面的研究，E?mail：fantasticmin＠126．com。

收稿日期：2015－10－22。

中圖分類號：TH133. 33；TH17

文獻標識碼：A

DOI：10. 3969／j. issn. 1672-0792. 2016. 01. 008