基于脈沖和時(shí)滯效應(yīng)的擬線性雙曲系統(tǒng)的(強(qiáng))振動(dòng)性分析*

羅李平， 羅振國(guó)， 曾云輝

(衡陽(yáng)師范學(xué)院數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，湖南 衡陽(yáng) 421002)

?

基于脈沖和時(shí)滯效應(yīng)的擬線性雙曲系統(tǒng)的(強(qiáng))振動(dòng)性分析*

羅李平， 羅振國(guó)， 曾云輝

(衡陽(yáng)師范學(xué)院數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，湖南 衡陽(yáng) 421002)

摘要：脈沖偏微分系統(tǒng)能夠成功地應(yīng)用于力學(xué)、理論物理、化學(xué)及人口動(dòng)力學(xué)、生物工程、最優(yōu)控制和經(jīng)濟(jì)學(xué)等方面的數(shù)學(xué)模擬。振動(dòng)性理論作為脈沖偏微分系統(tǒng)定性理論的重要分支之一，對(duì)其進(jìn)行研究具有極大的理論意義與實(shí)用價(jià)值。本文考慮一類基于脈沖和時(shí)滯效應(yīng)的擬線性雙曲系統(tǒng)的(強(qiáng))振動(dòng)性問(wèn)題，直接從(強(qiáng))振動(dòng)的定義出發(fā)，借助新的處理擬線性擴(kuò)散項(xiàng)的技巧、Green散度定理和第二類邊界條件把這類系統(tǒng)解的振動(dòng)問(wèn)題轉(zhuǎn)化為脈沖時(shí)滯微分不等式不存在最終正解的問(wèn)題，并利用二階脈沖時(shí)滯微分不等式的某些結(jié)果，建立了該類系統(tǒng)在第二類邊界條件下所有有界解(強(qiáng))振動(dòng)的若干充分判據(jù)，結(jié)論充分地表明系統(tǒng)振動(dòng)是由脈沖量和時(shí)滯量引起的，“強(qiáng)振動(dòng)性”的判別條件比“振動(dòng)性”的判別條件更強(qiáng)些。

關(guān)鍵詞：雙曲系統(tǒng)；(強(qiáng))振動(dòng)性；擬線性擴(kuò)散項(xiàng)；脈沖；時(shí)滯

引用格式：羅李平， 羅振國(guó)， 曾云輝. 基于脈沖和時(shí)滯效應(yīng)的擬線性雙曲系統(tǒng)的(強(qiáng))振動(dòng)性分析[J]. 中國(guó)海洋大學(xué)學(xué)報(bào)(自然科學(xué)版)， 2016, 46(4)： 149-152.

LUO Li-Ping, LUO Zhen-Guo, ZENG Yun-Hui. (Strong) Oscillation analysis of quasilinear hyperbolic systems based on effect of impulse and delay[J]. Periodical of Ocean University of China, 2016, 46(4): 149-152.

脈沖現(xiàn)象作為一種瞬時(shí)突變現(xiàn)象，在現(xiàn)代科技各領(lǐng)域的實(shí)際問(wèn)題中普遍存在，且往往對(duì)實(shí)際問(wèn)題的規(guī)律產(chǎn)生本質(zhì)的影響。因此，在建立數(shù)學(xué)模型對(duì)這些實(shí)際問(wèn)題進(jìn)行研究時(shí)，必須充分考慮脈沖現(xiàn)象的作用，這類數(shù)學(xué)模型往往可歸結(jié)為脈沖偏微分系統(tǒng)。它比通常連續(xù)微分系統(tǒng)所表達(dá)的模型研究起來(lái)要困難得多，除了一般的理論困難外，可能還出現(xiàn)在擾動(dòng)時(shí)刻不固定時(shí)滯系統(tǒng)常常產(chǎn)生的不斷脈沖打擊現(xiàn)象，這使得系統(tǒng)中原來(lái)保持的一些好的性質(zhì)被脈沖的干擾而破壞。盡管如此，但脈沖偏微分系統(tǒng)表達(dá)了許多連續(xù)微分系統(tǒng)中無(wú)法表達(dá)的具有實(shí)際背景的數(shù)學(xué)模型，在物理學(xué)、電磁學(xué)、生態(tài)學(xué)及人口動(dòng)力學(xué)以至于經(jīng)濟(jì)學(xué)中的許多數(shù)學(xué)模型都需要它來(lái)表達(dá)。因此，研究脈沖偏微分系統(tǒng)在理論和應(yīng)用兩方面都有重要意義。近年來(lái)對(duì)脈沖偏微分系統(tǒng)振動(dòng)性理論的研究引起了人們的極大關(guān)注，已陸續(xù)有一些很好的研究工作發(fā)表[1-6]。但相對(duì)而言，關(guān)于脈沖偏微分系統(tǒng)的強(qiáng)振動(dòng)的研究還不多見(jiàn)[7-9]。本文的目的是研究如下一類特殊的基于脈沖和時(shí)滯效應(yīng)的擬線性雙曲系統(tǒng)(1)在第二類邊界條件(2)下有界解的(強(qiáng))振動(dòng)性，利用新的處理擬線性擴(kuò)散項(xiàng)的技巧及二階脈沖時(shí)滯微分不等式的某些結(jié)果，獲得了判別該類系統(tǒng)所有有界解(強(qiáng))振動(dòng)的若干充分條件，所得結(jié)果充分表明系統(tǒng)振動(dòng)是由脈沖和時(shí)滯效應(yīng)引起的。

(1)

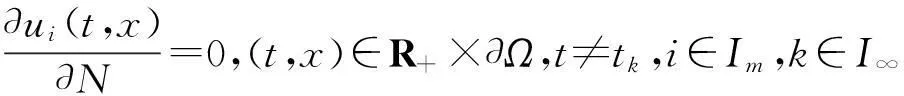
(2)

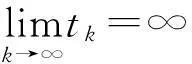
在本文中，對(duì)系統(tǒng)(1)總假定下列條件成立：

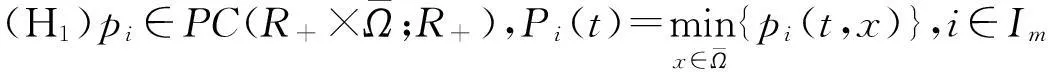
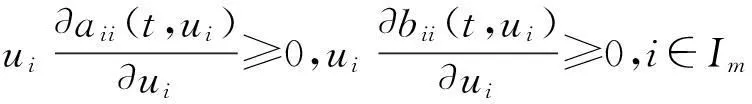
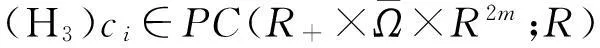
ci(t,x,ξ1,…,ξi,…,ξm,η1,…,ηi,…,ηm)=

ci(t,x,ξ1,…,-ξi,…,ξm,η1,…,-ηi,…,ηm)=

-ci(t,x,ξ1,…,ξi,…,ξm,η1,…,ηi,…,ηm)，i∈Im。

1有關(guān)定義、引理及記號(hào)

定義1稱向量函數(shù)u(t,x)=(u1(t,x),u2(t,x),…,um(t,x))T為邊值問(wèn)題(1)～(2)的解，若對(duì)i∈Im，ui(t,x)滿足：

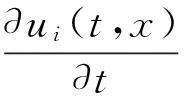
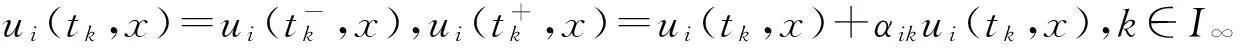
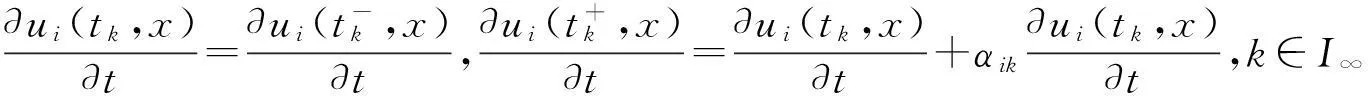
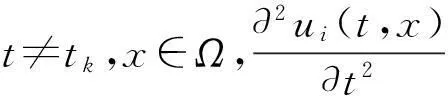
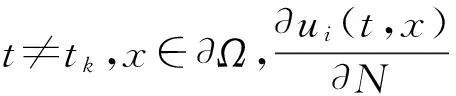
定義2稱數(shù)值函數(shù)ν(t,x)：G→R為非振動(dòng)的，若它最終為正或最終為負(fù)；反之，稱ν(t,x)為振動(dòng)的。稱向量函數(shù)u(t,x)：G→Rm為非振動(dòng)的，若它的每一分量都是非振動(dòng)的；稱向量函數(shù)u(t,x)：G→Rm為振動(dòng)的，若它至少有一分量作為數(shù)值函數(shù)是振動(dòng)的。稱向量函數(shù)u(t,x)：G→Rm為強(qiáng)振動(dòng)的，若它的每一個(gè)分量作為數(shù)值函數(shù)都是振動(dòng)的。

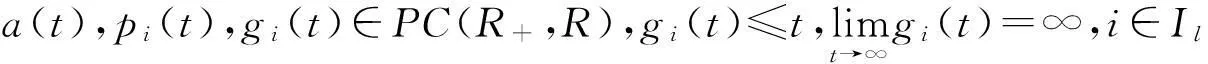
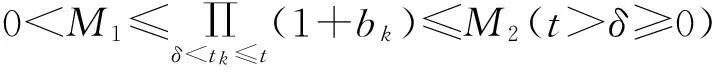
且有

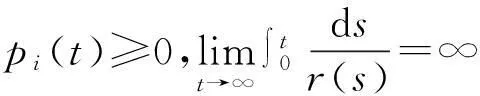
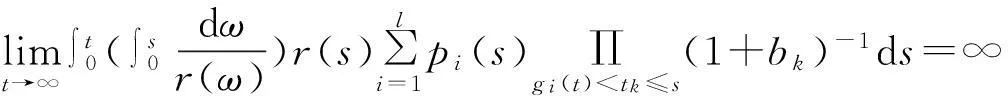
則脈沖時(shí)滯微分不等式

為敘述方便，引入記號(hào)：Ui(t)=∫Ωui(t,x)dx，t≥0，i∈Im。

2主要結(jié)果及其證明

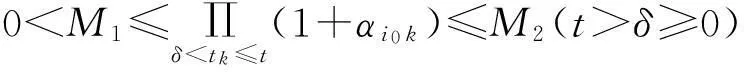
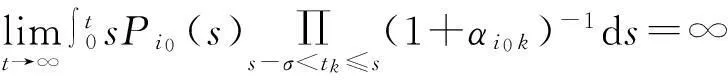
(3)

則系統(tǒng)(1)～(2)的所有非零有界解在區(qū)域G內(nèi)振動(dòng)。

證明(用反證法)假設(shè)系統(tǒng)(1)～(2)有一個(gè)非振動(dòng)的有界解u(t,x)=(u1(t,x),u2(t,x),…,um(t,x))T，則?i∈Im，u(t,x)在G內(nèi)非振動(dòng)，當(dāng)然也有ui0(t,x)在G內(nèi)非振動(dòng)。不失一般性，設(shè)ui0(t,x)最終為正，于是存在T>0，使得?(t,x)∈[T,∞)×Ω，有ui0(t,x)>0，ui0(t-τ,x)>0，ui0(t-σ,x)>0，ui0(t-ρ,x)>0。

考慮下面的方程：

(4)

(Ⅰ)當(dāng)t≥T，t≠tk，k∈I∞時(shí)，對(duì)(4)式的第一式兩邊關(guān)于x在Ω上積分，有

∫Ωpi0(t,x)ui0(t-σ,x)dx-

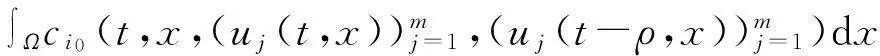
(5)

由Green公式，邊值條件(2)及條件(H2)有

∫Ωai0i0(t,ui0(t,x))Δui0(t,x)dx=

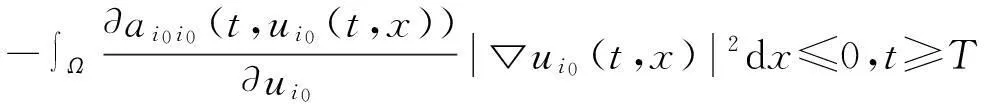
∫Ωai0j(t,uj(t,x))Δuj(t,x)dx=

其中dS是?Ω上的面積元素，

即

t≥T，j∈Im。

(6)

同理

∫Ωbi0j(t,uj(t-τ,x))Δuj(t-τ,x)dx=

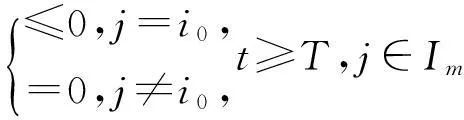
(7)

由條件(H3)易知

(8)

因此由(5)～(8)式及條件(H1)可得

U″i0(t)+Pi0(t)Ui0(t-σ)≤0，t≥T。

(9)

(Ⅱ)當(dāng)t≥T，t=tk，k∈I∞時(shí)，由(4)式中的脈沖條件，結(jié)合條件(H4)及定義1.1中的條件①可得

∫Ωui0(tk,x)dx=αi0k∫Ωui0(tk,x)dx=αi0kUi0(tk)，

即

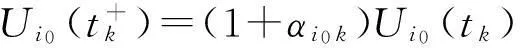
(10)

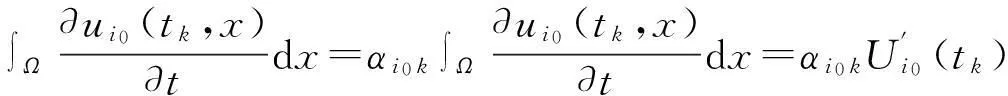
即

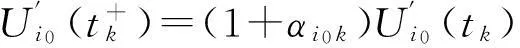
(11)

從而可知脈沖時(shí)滯微分不等式(9)～(11)有最終有界正解Ui0(t)。另一方面，結(jié)合條件(4)，由引理1知，脈沖時(shí)滯微分不等式(9)～(11)無(wú)最終有界正解，矛盾。

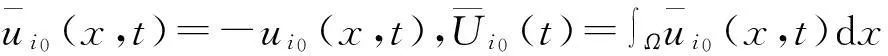
利用上面的結(jié)論，很容易得到下面的關(guān)于系統(tǒng)(1)～(2)強(qiáng)振動(dòng)的結(jié)論。限于篇幅，其證明在此略去。

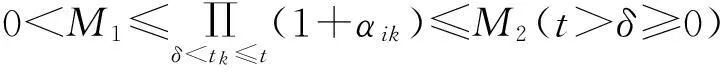
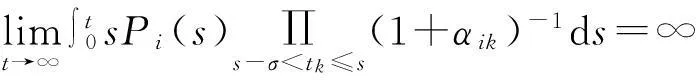
則系統(tǒng)(1)～(2)的所有非零有界解在區(qū)域G內(nèi)強(qiáng)振動(dòng)。

3結(jié)語(yǔ)

本文討論了一類擬線性脈沖時(shí)滯雙曲系統(tǒng)(1)～(2)非零有界解的(強(qiáng))振動(dòng)性問(wèn)題，所用方法異于參考文獻(xiàn)[1-6]中所用的通常的垂直相加法，但仍然建立了判別這類系統(tǒng)每個(gè)非零有界解(強(qiáng))振動(dòng)的顯式充分性條件，結(jié)果充分反映了脈沖量和時(shí)滯量在系統(tǒng)(強(qiáng))振動(dòng)中的決定性作用，這是一個(gè)重要的結(jié)論。由本文結(jié)果易知，若系統(tǒng)(1)～(2)強(qiáng)振動(dòng)，則系統(tǒng)(1)～(2)必振動(dòng)。“強(qiáng)振動(dòng)性”的判別條件比“振動(dòng)性”的判別條件更強(qiáng)些。本文結(jié)果可為解決生物學(xué)、物理學(xué)、工程學(xué)、氣象學(xué)、醫(yī)學(xué)、化學(xué)和控制理論等學(xué)科領(lǐng)域中的一些實(shí)際問(wèn)題提供數(shù)學(xué)理論依據(jù)和科學(xué)基礎(chǔ)。

參考文獻(xiàn)：

[1]羅李平, 羅振國(guó), 曾云輝. 基于脈沖控制的非線性時(shí)滯雙曲系統(tǒng)的振動(dòng)分析[J]. 系統(tǒng)科學(xué)與數(shù)學(xué), 2013, 33(9): 1024-1032.

LuoLP,LuoZG,ZengYH.OscillationAnalysisofnonlineardelayhyperbolicsystemsbasedonimpulsivecontrol[J].JournalofSystemandMathematicalScience, 2013, 33(9): 1024-1032.

[2]LuoLP,LiaoJD,GaoZH.Oscillationofsystemsofimpulsivedelayhyperbolicequations[J].InternationalJournalofAppliedMathematicsandApplications, 2008, 1(2): 147-154.

[3]羅李平. 具非線性擴(kuò)散系數(shù)的脈沖時(shí)滯雙曲型方程組的振動(dòng)性[J]. 自然科學(xué)進(jìn)展, 2008, 18(3): 341-344.

LuoLP.Oscillationofsystemsofimpulsivedelayhyperbolicequationswithnonlineardiffusioncoefficient[J].ProgressofNaturalScience, 2008, 18(3): 341-344.

[4]羅李平, 歐陽(yáng)自根. 脈沖中立型時(shí)滯拋物偏微分方程組的振動(dòng)準(zhǔn)則[J]. 應(yīng)用數(shù)學(xué)學(xué)報(bào), 2007, 30(5): 822-830.

LuoLP,OuyangZG.Oscillationcriteriaofsystemsofimpulsiveneutraldelayparabolicpartialdifferentialequations[J].ActaMathematicaeApplicataeSinica, 2007, 30(5): 822-830.

[5]LuoLP,PengBY,YangL.Oscillationofsystemsofimpulsivedelayparabolicequationsaboutboundaryvalueproblems[J].AnnofDiffEqs, 2007, 23(4): 470-476.

[6]LuoLP.Oscillationtheoremofsystemsofquasilinearimpulsivedelayhyperbolicequations[J].NortheastMathJ, 2007, 23(3): 255-262.

[7]羅李平, 俞元洪. 具擬線性擴(kuò)散系數(shù)的脈沖中立型拋物系統(tǒng)的(強(qiáng))振動(dòng)性[J]. 振動(dòng)與沖擊, 2011, 30(8): 183-186.

LuoLP,YuYH. (Strong)oscillationforsystemsofimpulsiveneutralparabolicequationswithquasilineardiffusioncoefficient[J].JournalofVibrationandShock, 2011, 30(8): 193-196.

[8]ZhangYT,LuoQ.Ontheforcedoscillationofsolutionsforsystemsofimpulsiveneutralparabolicdifferentialequationswithseveraldelays[J].JofMath. (PRC), 2006, 26(3): 272-276.

[9]LiWN.Ontheforcedoscillationofsolutionsforsystemsofimpulsiveparabolicdifferentialequationswithseveraldelays[J].JComputApplMath, 2005, 181(1): 46-57.

[10]YanJR.Oscillationpropertiesofasecond-orderimpulsivedelaydifferentialequation[J].ComputersMathApplic, 2004, 47: 253-258.

AMS Subject Classifications：35B05,35R12,35L99

責(zé)任編輯陳呈超

(Strong) Oscillation Analysis of Quasilinear Hyperbolic Systems Based on Effect of Impulse and Delay

LUO Li-Ping, LUO Zhen-Guo, ZENG Yun-Hui

(College of Mathematics and Statistics, Hengyang Normal University, Hengyang 421002, China)

Abstract：Impulsive partial differential systems can be successfully used for mathematical simulation in mechanics, theory physics, chemistry, population dynamics, biotechnology, optimal control and economics, etc. The oscillation theory is the one of the important branches of qualitative theory of impulsive partial differential systems. Therefore, it is of great theoretical and practical value to research the oscillation of partial functional differential equations. In this paper, the (strong) oscillation problems for a class of quasilinear hyperbolic systems based on the effect of impulse and delay are considered. Starting from the definition of oscillation directly, the oscillatory problems to the systems are reduced to the problem of which impulsive delay differential inequality hasn’t eventually position solution by employing a new technique of treating quasilinear diffusion term and Green’s divergence theorem and second boundary condition, and thereby some sufficient criteria are obtained for the (strong ) oscillation of all bounded solutions of such systems under second boundary condition via some results of second order impulsive delay differential inequality. The conclusions fully indicate that the system oscillation are caused by impulse and delay, and the criterion of strong oscillation is more sharp than the one of oscillation.

Key words：hyperbolic system; (strong) oscillation; quasilinear diffusion term; impulse; delay

DOI：10.16441/j.cnki.hdxb.20140067

中圖法分類號(hào)：O175.27

文獻(xiàn)標(biāo)志碼：A

文章編號(hào)：1672-5174(2016)04-149-04

作者簡(jiǎn)介：羅李平(1964-)，男，教授，研究方向：(脈沖)偏微分系統(tǒng)解的性態(tài)。E-mail:luolp3456034@163.com

收稿日期：2014-03-03；

修訂日期：2015-12-10

*基金項(xiàng)目：湖南省“十二五”重點(diǎn)建設(shè)學(xué)科項(xiàng)目(湘教發(fā)[2011]76號(hào))；湖南省普通高校青年骨干教師培養(yǎng)對(duì)象項(xiàng)目(湘教通[2015]361號(hào))；湖南省自然科學(xué)基金面上項(xiàng)目(2016JJ2008)資助

Supported by the Construct Program of the Key Discipline in Hunan Province([2011]76)， the Program of Hunan Province Ordinary University Youth Backbone Teacher Training Object([2015]361) ; The Program of Hunan Province Natural Science Foundation(2016JJ2008)