基于天線相關性的信道估計方法

北京郵電大學無線通信教研中心 北京 100876

引言

在3D MIMO系統中，特別是大規模MIMO系統中，基站端部署的天線數量會大量增加，系統容量獲得大幅度地提升[1-3]。為保證系統整體的通信性能，信道估計的重要性不言而喻，它所提供的瞬時信道響應能夠幫助接收端準確地恢復出發送端的消息。在基于導頻的信道估計技術(Pilot Aided Channel Estimation，PACE)中，維納濾波算法因其具有最小的均方誤差(Mean Square Error，MSE)從而在眾多信道估計算法中脫穎而出，成為最優的信道估計方法。然而，維納濾波算法是在犧牲了算法復雜度的基礎上實現了最優估計性能，因此，在實際應用中需要做出一定程度的簡化：文獻[4]中將原有的維納濾波方法轉變為利用多個級聯的一維維納濾波器來達到減少復雜度的目的。文獻[5]中提出一種新的信道模型，在此基礎上提出新型的導頻輔助方法。文獻[6-9]中利用時域頻域空域三維采樣定理以及信道空間相關性來完成信道估計。但是，上述方法都是在二維信道模型的基礎上研究的，然而三維的信道模型更加貼近現實的通信環境，對其研究是十分必要；因此，本文在研究三維信道模型基礎上提出了一種基于天線相關性的信道估計方法。

1 MIMO-OFDM系統

MIMO-OFDM系統就是將MIMO技術與OFDM技術相結合而成的新系統。由于MIMO技術運用多個發射與接收天線[10]，因此，它在空間中產生獨立的并行信道并在不增加頻譜資源和發射功率的情況下，可以實現多路數據流的同時傳輸，可以成倍地提升系統信道容量，可以提高系統的頻譜利用效率，以及可以加快系統的傳輸速率；而OFDM技術能夠在頻域內將頻率選擇性信道轉換為平坦信道[11]，它在一定程度上可減小多徑衰落帶來的影響，并且OFDM技術可將信道分解為若干正交的子信道，將高速數據信號轉換為低速子數據流，以便減少子信道之間的相互干擾。由于每個子信道上的信號帶寬都小于信道的相干帶寬，因此，每個子信道上都可以看作為平坦衰落，有效地減少了碼間干擾，而且由于每個子信道帶寬僅僅是原信道帶寬的一部分，這使得信道均衡變得相對容易，極大地提升了系統的接收性能。

通過空時編碼技術相結合的MIMO-OFDM系統不僅能夠提高無線通信系統的通信容量和傳輸速率，而且還可以有效地抵抗信道衰落帶來的影響。可以說，MIMOOFDM系統有著非常廣闊的應用前景，在諸多的無線信道高速數據傳輸解決方案中特點鮮明、優勢明顯，是現代通信系統(4G)乃至未來通信系統(5G)中最關鍵的技術之一。

2 3D信道模型及天線相關性分析

2.1 3D信道模型

考慮如圖1所示的坐標系[12-13]：以正東方向為x軸正方向，以垂直地面朝上為z軸正方向，水平角?的起始位置為x軸，沿x→y方向為?增大的方向；俯仰角θ的起始位置為xy平面，沿平面向上的方向為θ增大的方向；G(?,θ)為電磁波在方向上的增益；a、b、c、d分別為位于原點和3個坐標軸上的4個極化天線，天線i的坐標可以表示為(xi,yi,zi)。

考慮基站到移動臺的下行通信過程，在圖1所示坐標系中，WINNER Ⅱ提出的單極化信道模型表示為[14]：

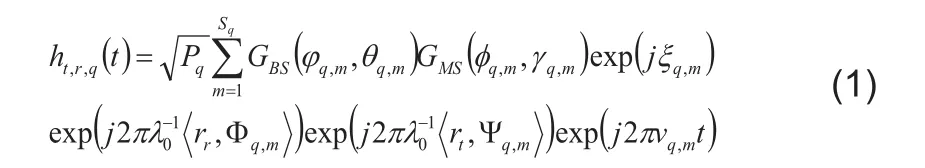
其中，Pq表示的是第q條主徑的功率值。(?q,m ,θq,m)和(φq,m γq,m)分別表示的是第q條主徑第m條子徑的發射角(Angel of Department，AoD)和到達角(Angel of Arrive，AoA)。GBS(?q,m ,θq,m)和GMS(φq,m γq,m)表示的是在基站端以及接收的天線分別在第q條主徑第m條子徑上的獲得的增益值。為了后文研究以及仿真計算簡便，我們統一規定無論是基站端還是接收端的天線增益都相同且為1。ξq,m表示的是服從[0,2π]均勻分布的無線電磁波隨機初始相位值，它是無線電磁波自身的屬性。νq,m代表了與接收端物體運動有關的多普勒頻率值。

2.2 天線相關性及相關系數

圖1 三維天線陣列坐標系

由于無線信道中每條徑的統計獨立性，多徑經疊加后的相關系數等于每條徑的相關系數的加權平均值。基于這一點接下來僅分析其中一條徑q包含Sq個子徑的情況，其它徑的分析情況類似，不做贅述。考慮基站側兩發射天線S1、S2到移動臺側天線兩個空間信道以及兩個空間信道的信道響應hu,s1,q和hu,s2,q。用ρs1,s2,q表示上述兩個信道的第q徑的相關系數[14-15]，則：

下面將簡要說明在三維空間中當S1、S2排列不同時，ρs1,s2,q的具體表達式：

2.2.1 兩天線沿水平方向排列

沿x軸排列的情形如圖1中的天線a和b，沿y軸排列的情形如圖1中的天線a和c，這兩種情況分析過程完全一樣，區別僅在于相對的坐標不同，因此這里分析沿x軸排列的情形，將式(1)代入式(2)，可得分母項[14-15]：

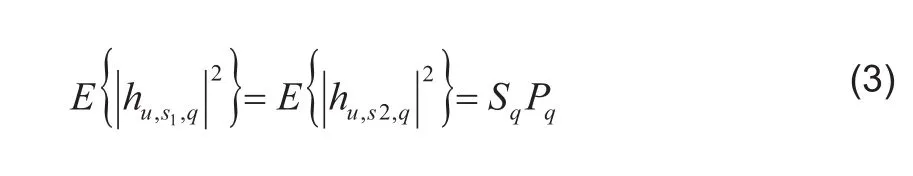
其中Sa表示子徑的個數，Pa為第q條主徑的功率，再將天線坐標代入式(3)，可得分子項：

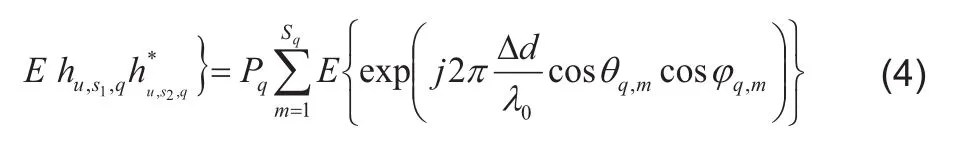
式(4)的期望計算是對俯仰角θq,m和水平角?q,m來進行的，后文中分別用θ和?來表示，根據標準模型的定義和實測數據結論，對于俯仰角θ和?水平角，簇內角度都服從均值為μ，標準差為角度擴展σ的拉普拉斯分布。若?的均值為μ?，標準差為σ?，θ的均值為μθ，標準差為σθ，式(4)中的期望計算如下：

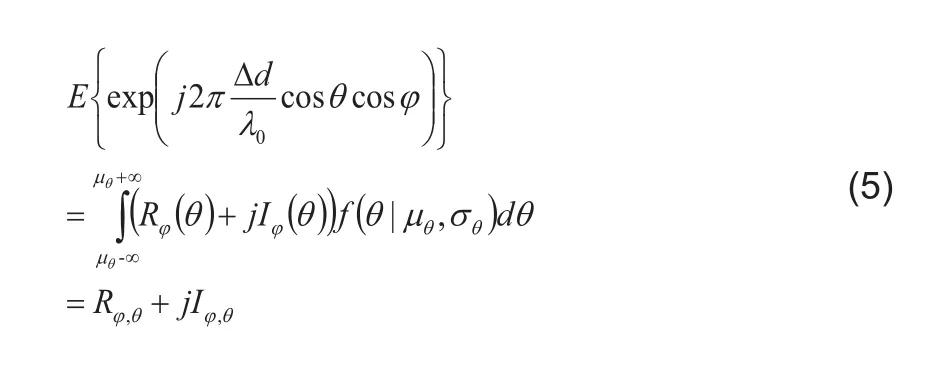
式(5)中包含兩重積分：第一重積分是對水平角?進行的，得到R?(θ)和I?(θ)；第二重積分是對俯仰角θ進行的，得到Rθ,?和Iθ,?。將雙重積分進行計算后代入式(2)可得第q徑相關系數：

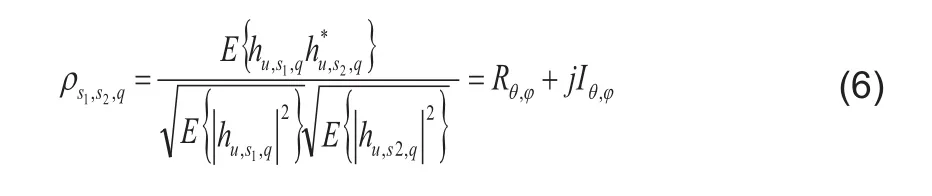
2.2.2 兩天線沿豎直方向排列

沿軸排列的情況如圖1中的天線a和d。與2.2.1中的計算步驟類似，分別計算式(2)中的分子和分母，對分子再次計算雙重積分，積分過程也與2.2.1中類似，這里就不再詳細說明。

由于式(2)表明的是兩根天線每條徑之間的相關系數，由于無線信道中每條徑的統計獨立性，多徑經疊加后的相關系數等于每條徑的相關系數的加權平均值，即：其中，N為徑數，q為徑的權值。此外，兩天線之間的相關系數也可以表示為[14]：

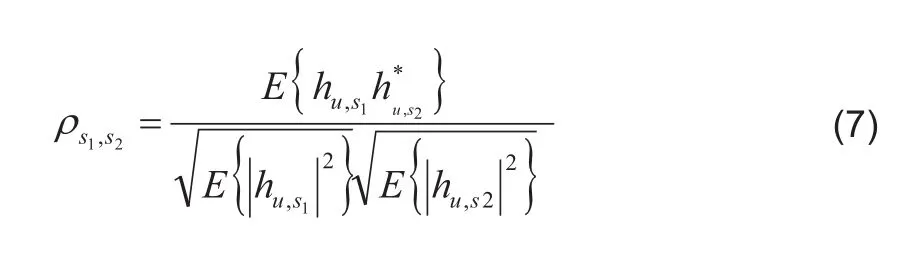
由式(7)我們可以知道兩天線之間的相關系數與各自的信道響應之間有著密切的關系，因此，我們可以利用天線間的相關性來完成信道估計。

3 天線相關性信道估計方法

當基站端部署的天線數量大量增加時，如果繼續沿用傳統的信道估計方法則會造成巨大的導頻開銷，導致資源的浪費；因此，如何減少導頻的開銷成為解決3D MIMO系統信道估計方法的關鍵環節。文獻[12]中提出一種基于面陣天線分解的方法來完成信道估計，通過對面陣天線陣列信道響應的分解，把面陣天線列陣響應分解為某一行和某一列響應的和，從而到達減少導頻開銷的目的。但該方法把導頻信息都集中在某一行和某一列上，在信噪比較低時估計結果的精度會受到很大影響；因此，本文在減少導頻開銷的前提下，提出基于天線相關性的信道估計方法以求在低運算復雜度下達到較高的估計精度。

由上一節的分析可知，當天線陣列中的天線陣元之間的間距足夠小且簇內的水平角度與俯仰角度都存在一個比較小的角度擴展時，天線陣元之間會存在相關性且這種相關性會反映到每個天線的信道響應中；因此，可以利用天線間的相關性來進行3D MIMO系統的信道估計。在基站端部署的天線產生較強相關性的場景下，該方法的具體步驟如下。

1)間隔均勻地在發送天線中放置導頻。將插入導頻的信息經調制、空時編碼、FFT以及加CP等步驟后由天線發送到無線多徑信道中。

2)接收端接收的信息經去CP、IFFT以及導頻分離等步驟后，對分離出的導頻信息進行信道估計。經過驗證，傳統的基于導頻的信道估計方法在三維信道環境下依然有效[12]；因此，對接收端接收后分離出的導頻信息利用LS、MMSE或者SVD算法進行信道估計和插值計算，得到放置導頻的天線的信道響應。

3)利用基于天線相關性的插值算法，恢復出未放置導頻的天線的信道響應。該方法計算過程如下：假設兩根天線S1、S2，它們之間的相關系數記為ρs1,s2。若在天線2上放置導頻且得出其信道相應后，將其代入式(7)，就可以得到天線1上的信道響應：

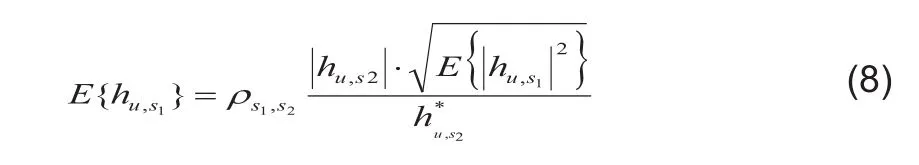
由于在實際計算過程中，我們不知道具體數值是多少，因此，我們先將其忽略掉計算剩余的部分，在最后的結果中再加以補償。為不失一般性，將該方法推廣到陣元數量更多的天線陣列中去，得到：假設發射端天線排列成u×ν的陣列，(i,j)表示其中的一根發射天線的索引ρi,j→m,n表示索引為(i,j)和(m,n)之間的信道響應相關系數。在發送端以空間采樣準則間隔的天線之間放入導頻，則在接收端首先利用傳統信道估計方法估計出放置導頻的天線的信道響應，然后未放置導頻天線的信道響應可由臨近的同行或者同列的放置導頻天線的信道響應的加權平均得出，其表示為：

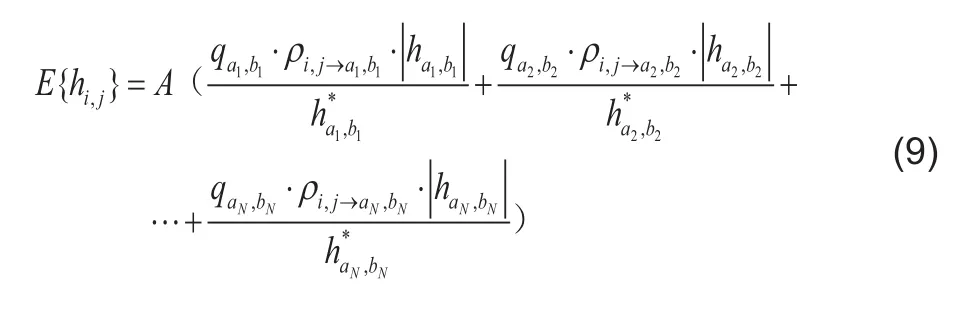
其中，ha1,b1，ha2,b2，…han,bn為和(i,j)在同行同列中最近的N個插入導頻的天線的信道響應，q為徑的加權系數，A為補償值。在實際的仿真過程中，在固定信噪比的情況下要預先設定一個可以接受的誤碼率。在進行第一次計算過程中設定A的值為一定值，然后在進行計算后的誤碼率統計時，若達到預先設定的誤碼率要求則無需再進行計算，否則按一定步長增大A的值再進行一次計算，直至滿足誤碼率要求為止。

4 仿真與結果分析

我們對第3節提出的基于天線相關性的信道估計方法進行仿真并驗證其性能。考慮一個8×8發一收系統，天線排布方式為沿圖1所示的xOy平面排列成8×8的方形天線陣列，在其中的部分天線上放置導頻，放置方式如圖2(a)、圖2(b)所示。

圖2(a) “菱形” 方式

圖2(b) “方形”方式

圖2中黑色部分代表放置導頻的天線，白色則代表未放置導頻的天線。仿真中的參數設置為：OFDM調制中IFFT子載波數為發送端發射天線之間的間隔為半波長；載波頻率為2GHz，符號持續時間子載波間隔為三維信道是由20條徑來組成的，每條徑又是由20條子徑來組成的。各徑的參數如表1所示。

在按照圖2所示的兩種導頻放置方式下，將該方法與維納濾波方法以及文獻[12]中提出的方法在誤碼率上進行對比，結果如圖3所示。

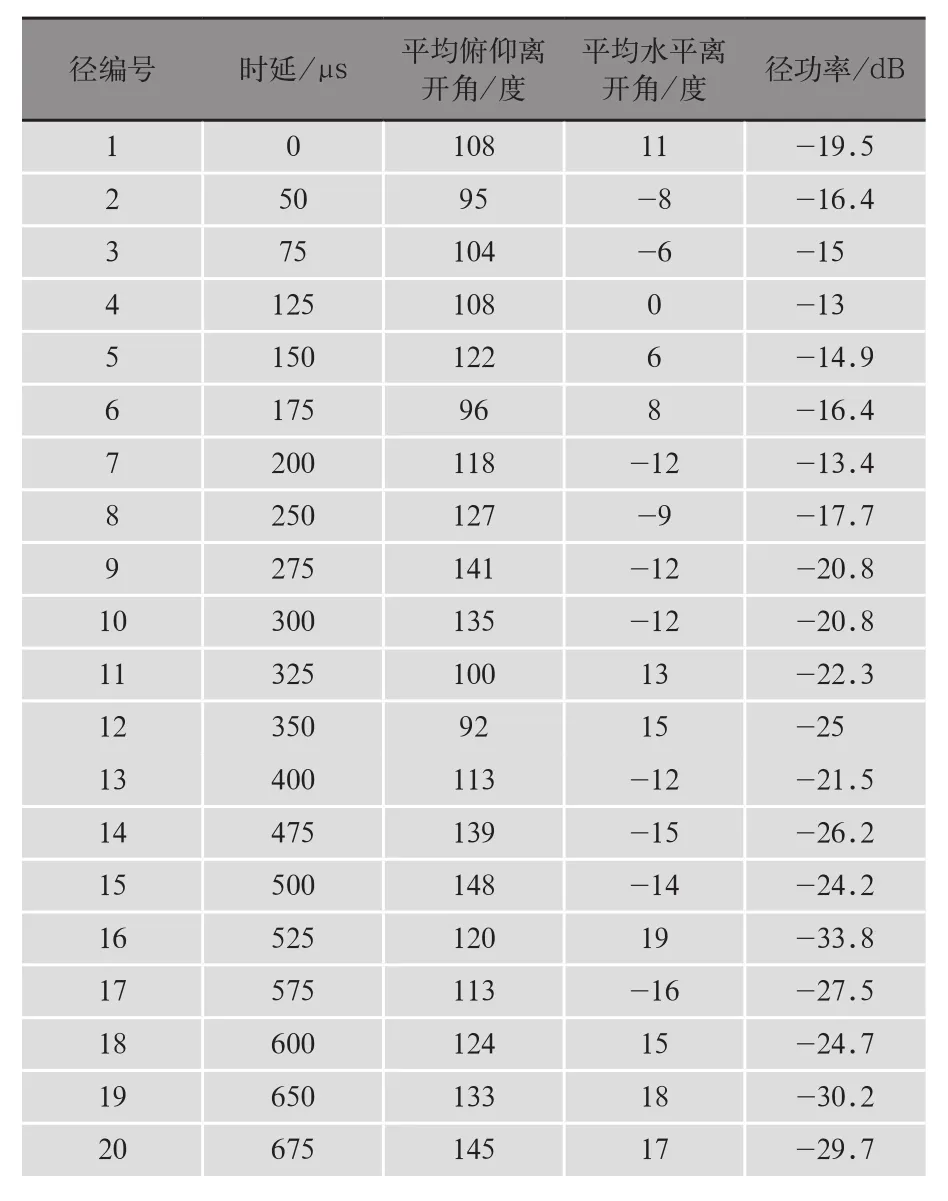
表1 3D信道各徑參數配置

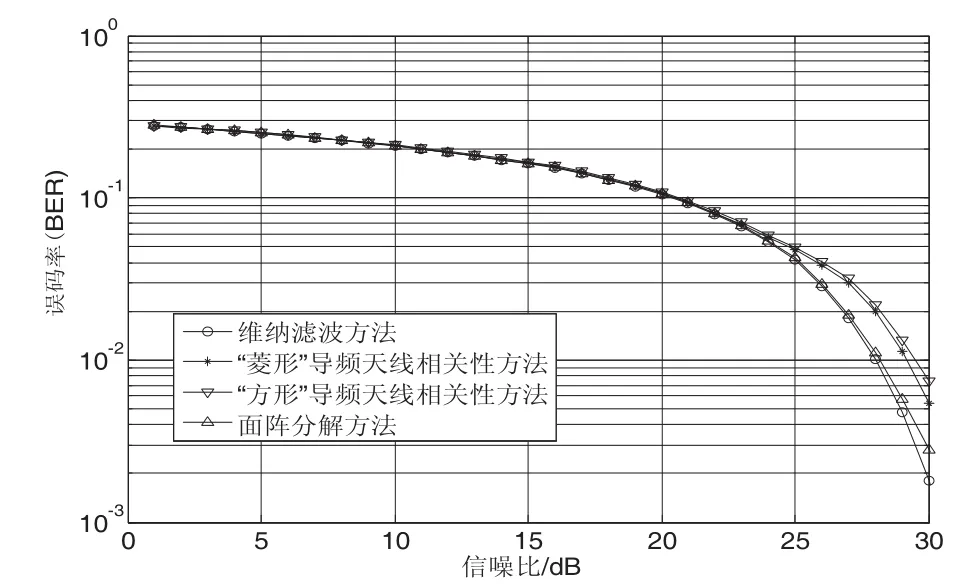
圖3 三種方法的誤碼率對比圖

從圖3中可以看出天線相關性算法在性能上很接近維納濾波方法，但是它與維納濾波方法相比減少了近一半的導頻開銷。在此基礎上，我們來探究三種方法的相對MSE性能，其結果對比如圖4所示。

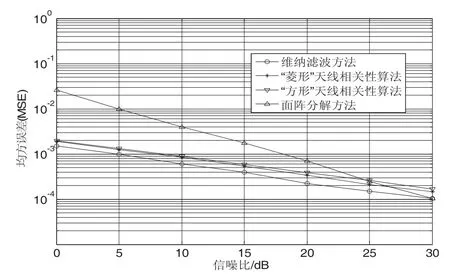
圖4 三種方法的MSE結果對比圖

從圖4中可以再次看出天線相關性方法在性能上很接近維納濾波算法，且在信噪比較低的時候相比于面陣分解方法有著較優的估計性能。在兩種不同的導頻放置方式下，“菱形”導頻相關性算法的性能略微好于“方形”導頻，究其原因就在于在“菱形”導頻放置方式下，未放置導頻的天線在進行相關性計算的時候可以利用周圍的至少三個天線上的結果，而在“方形”導頻放置方式下，只能利用同行或者同列上的兩個天線，所以其計算得到的結果精度不如前者。

然而，由第一節的分析可知：維納濾波算法的高精度是以犧牲算法復雜度為代價的，然而由第四節對天線相關性算法的推導中可知，該算法在計算復雜度上簡便許多。為有更直觀的對比，我們來探究在相同信噪比下三種算法的算法復雜度(即編程實現后算法中語句的執行頻度)，結果如表2所示。

表2 三種算法算法復雜度對比

其中，T(n)表示編程實現后算法中語句的執行頻度，n為天線數量。從表2中我們不難看出，相關性算法的算法復雜度是低于維納濾波算法的，并且和文獻[12]中提出的方法的算法復雜度相近。再結合圖5中的相對MSE對比結果可以看出相關性算法達成了在減少導頻開銷的基礎上實現了復雜度與估計精度的折中的目的。

5 總結

3D MIMO技術的興起與發展使得對于信道估計的精確度和時效性有了更高的要求。本文首先對于現有的信道估計方法進行了簡要分析，然后為解決在三維信道模型下的估計精確度與時效性這一問題，本文提出在特定場景下的基于天線相關性的信道估計方法并最終通過仿真驗證該算法在減少導頻開銷的基礎之上實現了結果精確度和算法復雜度上的折中。

參考文獻

[1] Nadeem Q U A, Kammoun A, Debbah M, et al. A Generalized Spatial Correlation Model for 3D MIMO Channels based on the Fourier Coefficients of Power Spectrums[J]. Signal Processing IEEE Transactions on,2015(63):3671-3686

[2] Ryden H, Razavi S M, Gunnarsson F, et al. Baseline performance of LTE positioning in 3GPP 3D MIMO indoor user scenarios[C]// Localization and GNSS (ICLGNSS), 2015 International Conference on. IEEE, 2015

[3] Cheng X, Yu B, Yang L, et al. Communicating in the real world: 3D MIMO[J]. IEEE Wireless Communications,2014, 21(4):136-144

[4] Choi J W, Lee Y H. Complexity-reduced channel estimation in spatially correlated MIMO-OFD Msystems[J].IEICE Trans.Commun.2006,E89-B(3):801-808

[5] Cheng C C, Chen Y C, Su Y T. Modeling and Estimation of Correlated MIMO-OFDM Fading Channels[J]IEEE International Conference on Commun. (ICC), 2011(7):1-5

[6] Auer G. 3D Pilot Aided Channel Estimation[C]//IEEE Wireless Commun and Networking Conference(WCNC),2009(4):1-6

[7] Auer G. Bandwidth efficient 3D pilot design for MIMO-OFDM[J]//European Wireless Conference,2010(4):701-705

[8] Auer G. 3D MIMO-OFDM Channel Estimation[J]//IEEE Trans on Commun, 2012,60(4):1-6

[9] 于國慶,段紅光.基于導頻的三維信道估計[J].電視技術,2014,38(5): 140-143

[10] 周炯槃,龐沁華,續大我,等.通信原理[M].北京:北京郵電大學出版社, 2008

[11] 啜鋼,王文博,常永宇,等.移動通信原理與系統[M].北京:北京郵電大學出版社,2009

[12] 何小丹.3D MIMO信道估計技術研究[D].北京:北京郵電大學信息與通信工程學院,2014

[13] CELTIC project WINNER+[J].D5.3:WINNER+ Final Channel Models, 2010(7):171-190

[14] 黎昌,姚俊良,蔡振合.三維MIMO陣列空間相關性分析[J].電信科學,2015(1):1-6

[15] 邵朝,劉蕊鵬.大規模MIMO:天線互耦與空間相關性分析[J].無線通信技術,2015,24(1):1-5