初中數學復習課的高效教學策略與建議
岑雪珍

步入初三,學生的學習任務隨著學科數目的增多和數學學科綜合性的增強,復習壓力無形增大,那么初中的數學復習課如何實施呢?筆者認為復習課應該注重學生思維的引導和訓練,為此嘗試著利用思維導圖來幫助學生優化初中數學的知識復習.
一、高效復習課的教學策略
1.借助于思維導圖實施復習課的備課
每節課都要充分準備后才能和學生一起探究,對于初中數學的復習課也不能外.筆者認為在復習課的備課過程中應該借助于思維導圖將教學目標、重點,以及難點統籌到教學設計中來,旨在讓復習課的條理性更為清晰,幫助學生構建出更為清晰的知識網絡,更好地應用知識解決與初中的數學知識相關的問題.
2.借助于思維導圖組織復習課的教學
備課與課堂實施一脈相承,筆者認為課堂組織過程應該和備課的過程一樣注重學生思維的程序性和知識的系統性.
(1)要求學生結合前面新課學習所得的數學概念、數學思想方法自主繪制出嚴謹的思維導圖,思維導圖凸顯出所復習的章節的重點、難點,并以此為數學復習的中心有層次地發散,凸顯出數學知識的層次性.
(2)在學生繪制思維導圖的基礎上進行講解和二次探究,讓學生展示出自己復習的思維過程,同時暴露出學生在復習過程中存在的知識和思維的缺陷,再以此為復習課的生長點讓學生以學習小組為單位進行分析和討論,從而實現對知識的認知更為完整,認識更為清晰,為順利解決數學問題打下堅實的基礎.
(3)在學生對知識全貌有所了解時,教師可以借助于多媒體或采用實物投影的方式將備課時預備的思維導圖給學生看,然后有針對性地設置例題、習題,引導學生在習題分析和問題解決的過程中完成圖式的聯結,提高學生解決問題的能力和數學思維能力.
3.注重復習課后的反思
在初中階段的數學學習過程中,學生會感到數學知識繁、雜,所以在復習課上必然存在知識及其應用過程中思維上的遺漏,所以課后,我們應該注重反思,教師通過對復習案例進行反思,彌補教學中存在的不足,從而提高教學質量.教師在實際教學的過程中進行反思,具有非常重要的意義,可以及時地發現教學中的不足,進而采取有效的措施進行改進,對學生進行有效的引導.
復習課后的反思除了教師的教學反思外,還有學生的復習的反思,學生反思自己復習過程中哪些知識還比較生疏,哪些方法的應用還比較生硬,自己在構建思維導圖的過程中還有哪些缺陷和概念聯系上的不足,便于完整的知識體系在頭腦中構建,同時也便于學習方法和經驗在頭腦中沉淀下來.反思的過程是教師引導學生對數學概念和思維導圖再認識和再探究的升華過程.
二、高效復習課的具體流程與案例
結合前面的分析,筆者將初中數學的高效復習課的課堂組織流程分為如下幾個部分,下面結合具體的案例:“二次函數”的復習進行分析.二次函數這部分內容是中考的難點問題,如何高效復習值得思考與探究.筆者在具體的復習實踐中進行了如下的安排:
1.設置開放型的問題情景,引導學生思維
在復習課的課前,要求學生對這部分內容自主預習,為了提高學生預習的實際效果,筆者設置了一個問題.
問題1 如圖1所示,這是某一個函數的圖象其中的一部分,請你注意觀察,看一看能獲取哪些信息?
設計意圖 這個問題的起點設置比較低,但是出口很寬,學生能夠聯系到的知識點比較多,有助于本節內容的復習.
2.構建活動
學生前面對問題1進行自主思考,形成一定的認識,這些認識拿到復習課堂上來交流,繼而形成對所復習知識的初步認識.
從學生反饋的信息來看,初淺的認識有如下幾個:
信息1:這個函數的圖象是開口向下,由此可知a<0;是軸對稱圖形,對稱軸為:直線x=1(開口的方向和對稱性).
信息2:這個函數的圖象經過(3,0)和(0,3)兩個點(特殊點).
信息3:從圖形上看,當x=1,y對應著最大值4(最值).
信息4:這個函數是二次函數,這個圖象為拋物線.
深入一些的認識有如下幾個:
信息5:我能判斷這個函數為二次函數,那么其一般形式y=ax2+bx+c,這個函數的圖象經過(0,3),很容易知道c=3.
信息6:對稱軸為:直線x=1,可知x=-b2a=1,所以得到b>0.同時根據對稱性,容易得到圖象與x軸的另一個交點為(-1,0).
信息7:根據圖象信息可以借助于待定系數法來求函數的關系式,借助于頂點式得y=-(x-1)2+4;一般式得y=-x2+2x+3;交點式得y=-(x-3)(x+1).
3.思維導圖的第一次完善
從學生的認識和交流的情況來看,對基本知識和規律復習還是可以的,筆者再拋出幾個問題,讓學生的思維和認識能夠第一次得以完善.
問題2:上面大家總結的方法很好,那么求二次函數的表達式的三種方法分別在什么時候用啊?
問題3:頂點式與一般式有什么內在的聯系?
問題4:一元二次方程是否與二次函數也存在內在的聯系?
通過前面的信息的提取與思考,加上后面這幾個問題的解決,學生的思維導圖出現了具有層次性的框架,層次有3:(1)對二次函數定義、三種形式的理解;(2)對二次函數的圖象及其形式的理解(這是重點);(3)對方程與函數關系的理解.
4.思維導圖的再一次完善
為了進一步發展學生的思維,繼續以問題的形式引導學生進行思考.
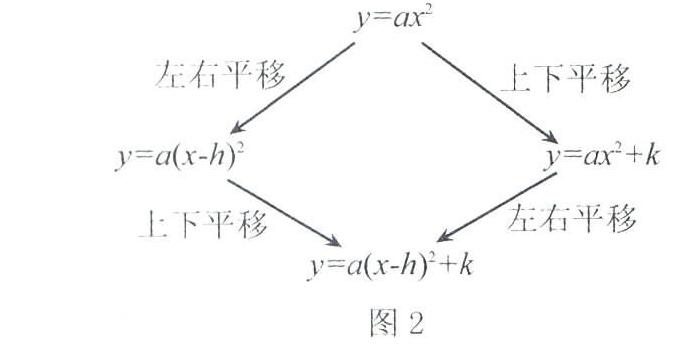
問題5:對于y=-(x-1)2+4的圖象可以由怎樣的函數圖象平移得到呢?有多少種平移方式呢?
學生進一步討論和歸納在原有思維導圖的基礎上加上第4個層次:(4)平移(具體圖式如圖2所示).
5.典型例題訓練
學生頭腦中已經有了圖式,接下來給學生提供例題,能夠促進學生復習中知識的內化.
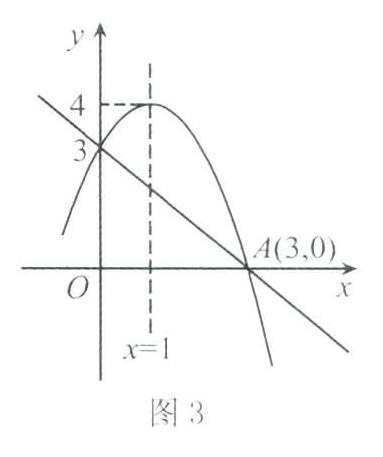
例題 二次函數y=ax2+bx+c和一次函數y=mx+n的圖象如圖3所示,若ax2+bx+c-(mx+n)=0,不解方程能寫出根嗎?
學生在解決這個例題的過程中實現了前面歸結圖式的應用,復習的實際效果也就最終落在了解決問題、檢查和評價自己的復習成果中去了.
教無定法,對于復習課亦是如此,本文所涉及到的僅僅是筆者的一點實踐體會與感悟,不當之處,還望專家同行雅正.

