基于并行遺傳算法的網(wǎng)絡(luò)最優(yōu)彌補(bǔ)模型

吳蓓

摘 要： 將攻擊圖與并行遺傳算法相結(jié)合，提出了一種基于并行遺傳算法的網(wǎng)絡(luò)最優(yōu)彌補(bǔ)模型（PGA?ONHM），該模型能得到目標(biāo)網(wǎng)絡(luò)系統(tǒng)的近似解。為了驗(yàn)證該模型的可行性、有效性和可擴(kuò)展性，從不同的分析角度進(jìn)行仿真驗(yàn)證，實(shí)驗(yàn)結(jié)果表明：并行遺傳算法的CPU消耗時(shí)間隨著初始屬性節(jié)點(diǎn)數(shù)量的增加呈多項(xiàng)式增加，隨著子群體數(shù)量的增加呈減小趨勢(shì)；無論是平均迭代次數(shù)還是單次迭代的平均計(jì)算時(shí)間，并行遺傳算法比經(jīng)典遺傳算法都要優(yōu)越；并行遺傳算法可以得到較好的加速比，能夠克服局部最優(yōu)解的問題，可以適用于大規(guī)模復(fù)雜的網(wǎng)絡(luò)系統(tǒng)。

關(guān)鍵詞： 網(wǎng)絡(luò)脆弱性； 攻擊圖； 網(wǎng)絡(luò)脆弱性彌補(bǔ)； PGA?ONHM

中圖分類號(hào)： TN915.08?34 文獻(xiàn)標(biāo)識(shí)碼： A 文章編號(hào)： 1004?373X（2016）05?0105?05

0 引 言

人類在享受互聯(lián)互通和信息共享帶來的便捷與效益的同時(shí)，網(wǎng)絡(luò)技術(shù)發(fā)展過程中對(duì)安全性的忽視，導(dǎo)致網(wǎng)絡(luò)環(huán)境中存在各式各樣的安全隱患，嚴(yán)重威脅著網(wǎng)絡(luò)運(yùn)營(yíng)及合法用戶的信息安全。因此，尋找并彌補(bǔ)威脅網(wǎng)絡(luò)關(guān)鍵資源的脆弱性是提高網(wǎng)絡(luò)安全性的一種有效方法。文獻(xiàn)[1]基于邏輯推理的方法，首先將最優(yōu)彌補(bǔ)求解問題轉(zhuǎn)化為布爾表達(dá)式；然后求解該布爾表達(dá)式的析取范式，從而得到所有的彌補(bǔ)措施；最后通過分析比較得到最優(yōu)彌補(bǔ)建議。該方法在最壞情況下具有不可避免的指數(shù)時(shí)間復(fù)雜度，無法應(yīng)用于網(wǎng)絡(luò)規(guī)模較大的真實(shí)目標(biāo)網(wǎng)絡(luò)系統(tǒng)。文獻(xiàn)[2]提出采用歸納有序二元決策圖（ROBDD）的方法求解最優(yōu)彌補(bǔ)。該方法可以有效地獲取攻擊圖的最優(yōu)彌補(bǔ)，但在該方法中，未對(duì)脆弱性進(jìn)行度量標(biāo)準(zhǔn)的說明，因此在實(shí)際應(yīng)用上具有一定的局限性。

由于求解最優(yōu)彌補(bǔ)問題是NP完全性問題，對(duì)于NP完全性問題，采用啟發(fā)式搜索方法可以更快地獲得結(jié)果。并行遺傳算法[3?6]具有以下優(yōu)勢(shì)：覆蓋面大，利于全局擇優(yōu)；對(duì)問題的依賴性較小，求解的魯棒性較好；具有并行計(jì)算的特點(diǎn)，可以用大規(guī)模的并行計(jì)算來提高計(jì)算速度；特別適用于復(fù)雜大系統(tǒng)問題的優(yōu)化求解，但其存在收斂速度慢、局部搜索能力差等不足之處。并行遺傳算法可以克服經(jīng)典遺傳算法的不足，提高遺傳算法求解的速度和質(zhì)量。基于此，本文將攻擊圖與并行遺傳算法相結(jié)合，提出了一種基于并行遺傳算法的網(wǎng)絡(luò)最優(yōu)彌補(bǔ)模型（Optimal Network Hardening Model Based on Parallel Genetic Algorithm，PGA?ONHM）。

3 實(shí)驗(yàn)結(jié)果與分析

為了驗(yàn)證PGA?ONHM模型的可行性、有效性和可擴(kuò)展性，本文從不同分析角度做了兩組實(shí)驗(yàn)，并對(duì)實(shí)驗(yàn)結(jié)果進(jìn)行了分析。實(shí)驗(yàn)環(huán)境如下：服務(wù)器PowerEDGE R710，操作系統(tǒng)RetHAT V5.4，內(nèi)存32 GB，CPU 2.26 GHz。

3.1 算法性能驗(yàn)證實(shí)驗(yàn)

由算法性能分析可知，該算法性能與目標(biāo)網(wǎng)絡(luò)系統(tǒng)中初始屬性節(jié)點(diǎn)數(shù)量[C，]迭代次數(shù)[D，]子群體[U]等參數(shù)有關(guān)。為了驗(yàn)證不同網(wǎng)絡(luò)環(huán)境下這些參數(shù)對(duì)算法性能的影響，在得到最優(yōu)解的前提下，分別設(shè)計(jì)了如下兩組實(shí)驗(yàn)。

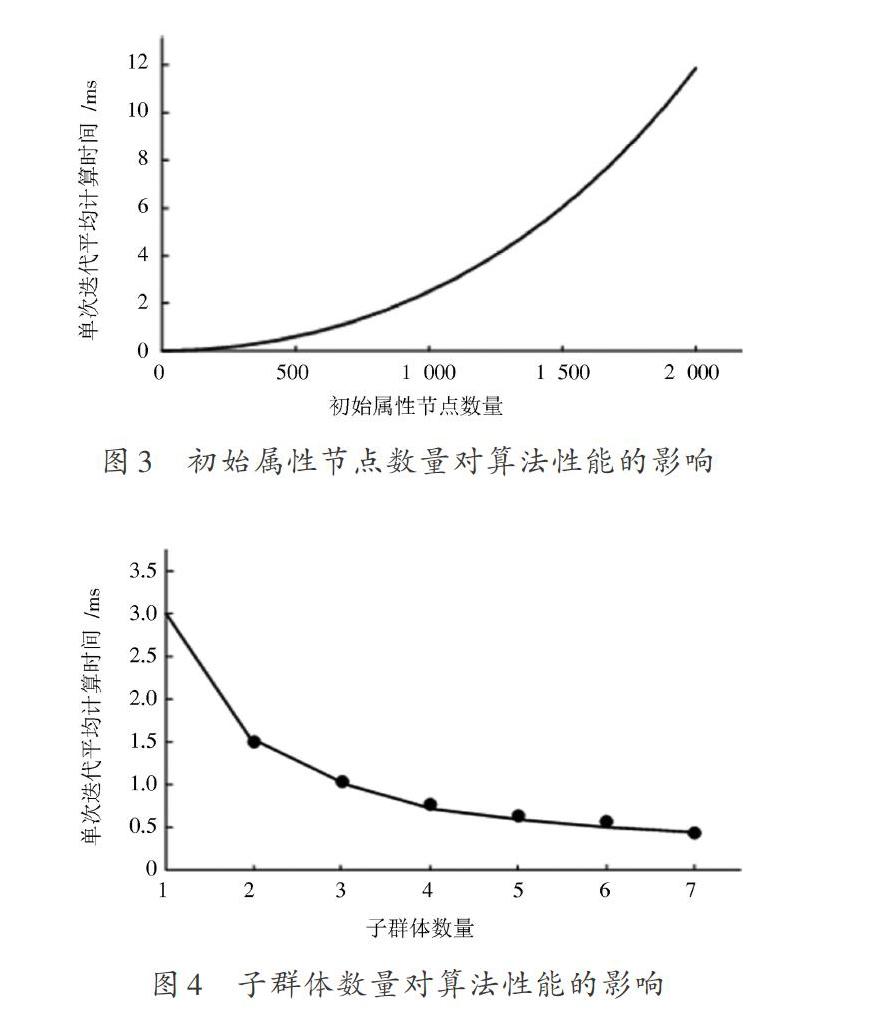
第一組實(shí)驗(yàn)驗(yàn)證初始屬性節(jié)點(diǎn)數(shù)量不同時(shí)，單次迭代的平均計(jì)算時(shí)間如圖3所示。由圖3可知，單次迭代的平均計(jì)算時(shí)間隨著初始屬性節(jié)點(diǎn)數(shù)量[C]的增加呈多項(xiàng)式增加趨勢(shì)。

第二組實(shí)驗(yàn)驗(yàn)證子群體數(shù)量（即處理器數(shù)量）對(duì)算法性能的影響。令初始屬性節(jié)點(diǎn)數(shù)量為500，當(dāng)子群體數(shù)量不同時(shí)，單次迭代的平均時(shí)間如圖4所示。由圖4可知，單次迭代的平均計(jì)算時(shí)間隨著[U]的增加呈減小趨勢(shì)。

由上述兩組實(shí)驗(yàn)結(jié)果可知，在PGA?ONHM模型中，算法CPU消耗的時(shí)間隨著初始屬性節(jié)點(diǎn)數(shù)量[C]的增加呈多項(xiàng)式增加趨勢(shì)，隨著子群體數(shù)量[U]的增加呈減小趨勢(shì)，實(shí)驗(yàn)結(jié)果與算法性能分析結(jié)果一致。

3.2 算法對(duì)比實(shí)驗(yàn)

（1） 經(jīng)典遺傳算法和并行遺傳算法對(duì)比實(shí)驗(yàn)，實(shí)驗(yàn)結(jié)果如表1所示。表1列出了在初始屬性節(jié)點(diǎn)數(shù)量不同的情況下，求解最優(yōu)彌補(bǔ)時(shí)兩種算法的平均迭代次數(shù)和單次迭代的平均計(jì)算時(shí)間。

從實(shí)驗(yàn)結(jié)果可以看出：一方面，針對(duì)同一目標(biāo)網(wǎng)絡(luò)環(huán)境，無論是平均迭代次數(shù)還是單次迭代的平均計(jì)算時(shí)間，并行遺傳算法比經(jīng)典遺傳算法都要優(yōu)越，其主要原因是在并行遺傳算法的具體實(shí)現(xiàn)過程中，首先將總?cè)后w分成若干子群體，然后將子群體分配到各自的處理機(jī)上，獨(dú)立地進(jìn)行遺傳算法的進(jìn)化操作，實(shí)現(xiàn)了從全局角度開發(fā)群體進(jìn)化的并行性，從而提高了計(jì)算效率；另一方面，并行遺傳算法具有良好的可擴(kuò)展性，當(dāng)初始屬性節(jié)點(diǎn)數(shù)量達(dá)到2 000時(shí)，單次迭代的平均計(jì)算時(shí)間也不過7 ms。

（2） 加速比實(shí)驗(yàn)。目前公認(rèn)的評(píng)價(jià)并行遺傳算法性能的指標(biāo)是加速比，即并行遺傳算法與經(jīng)典遺傳算法完成等量工作所耗時(shí)間的比例，它標(biāo)志著一個(gè)并行遺傳算法的好壞。本文在相同的硬件環(huán)境下，對(duì)同一目標(biāo)網(wǎng)絡(luò)環(huán)境通過改變處理器數(shù)量，進(jìn)行了加速比實(shí)驗(yàn)，實(shí)驗(yàn)結(jié)果如表2所示。加速比和處理器數(shù)量的關(guān)系如圖5所示。由圖5可知，加速比與處理器幾乎呈線性關(guān)系，因此，本文所提并行遺傳算法可以得到較好的加速比，是行之有效的并行手段。

4 結(jié) 論

PGA?ONHM模型通過建立數(shù)學(xué)模型將攻擊圖與并行遺傳算法相結(jié)合，得到最優(yōu)彌補(bǔ)的近似解。為了驗(yàn)證該模型的可行性、有效性和可擴(kuò)展性，本文從不同的分析角度做了兩組實(shí)驗(yàn)，實(shí)驗(yàn)結(jié)果表明：CPU消耗時(shí)間隨著初始屬性節(jié)點(diǎn)數(shù)量的增加呈多項(xiàng)式增加，隨著子群體數(shù)量的增加呈減小趨勢(shì)；無論是平均迭代次數(shù)還是單次迭代的平均計(jì)算時(shí)間，并行遺傳算法比經(jīng)典遺傳算法都要優(yōu)越；加速比與處理器呈線性關(guān)系；能夠克服局部最優(yōu)解的問題，可以適用于大規(guī)模復(fù)雜的網(wǎng)絡(luò)系統(tǒng)。

參考文獻(xiàn)

[1] JHA S， SHEYNER O， WING J M. Two formal analyses of attack graphs [C]// Proceedings of 15th IEEE Conference on Computer Security Foundations Workshop. [S.l.]： IEEE， 2002： 49?63.

[2] NOEL S， JAJODIA S， O′BERRY B， et al. Efficient minimum?cost network hardening via exploit dependency graphs [C]// Proceedings of 19th Annual Conference on Computer Security Applications. [S.l.]： IEEE， 2003： 86?95.

[3] WANG L Y， NOEL S， JAJODIA S. Minimum?cost network hardening using attack graphs [J]. Computer communications， 2006， 29（18）： 3812?3824.

[4] HOMER J. From attack graphs to automated configuration management： an iterative approach [R]. Kansas： Kansas State University Technical Report， 2008.

[5] SI J Q， ZHANG B， MAN D P， et al. Approach to making strategies for network security enhancement based on attack graphs [J]. Journal on communications， 2009， 30（2）： 123?128.

[6] CHEN F， WANG L Y， SU J S. An efficient approach to minimum?cost network hardening using attack graphs [C]// Procee?dings of 2008 the 4th International Conference on Information Assurance and Security. Naples： IEEE， 2008： 209?212.

[7] CHEN F， ZHANG Y， SU J S， et al. Two formal analyses of attack graphs [J]. Journal of software， 2010， 21（4）： 838?848.

[8] CHEN F. A hierarchical network security risk evaluation approach based on multi?goal attack graph [D]. Changsha： National University of Defense Technology， 2008.

[9] ALBANESE M， JAJODIA S， NOEL S. Time?efficient and cost?effective network hardening using attack graphs [C]// Proceedings of the 42nd IEEE/IFIP Annual International Conference on Dependable Systems and Networks. Boston： IEEE， 2012： 1?12.