基于瞬變平面熱源法的纖維熱導率測試

李 麗， 肖 紅， 程博聞， 槐向兵

(1. 天津工業大學 紡織學院, 天津 300387； 2. 后勤保障部軍需裝備研究所, 北京 100010；3. 江陰市紅柳被單廠有限公司, 江蘇 江陰 214432)

基于瞬變平面熱源法的纖維熱導率測試

李 麗1，2， 肖 紅2， 程博聞1， 槐向兵3

(1. 天津工業大學 紡織學院, 天津 300387； 2. 后勤保障部軍需裝備研究所, 北京 100010；3. 江陰市紅柳被單廠有限公司, 江蘇 江陰 214432)

為解決單纖維熱導率不易直接測試的難題，基于兩相復合介質串并聯等效熱導率物理模型，采用瞬變平面熱源法對環氧樹脂-纖維復合體系進行測試，并計算出單纖維軸向和徑向的熱導率。結果表明，采用該方法可獲得纖維熱導率，且纖維軸向的熱導率要明顯大于纖維徑向的熱導率，驗證了纖維熱學性能的各向異性。復合體系中兩相材料的熱導率差異、纖維所占體積比及物理模型、儀器的加熱功率、測試時間的設定等對纖維熱導率結果影響顯著。當纖維和樹脂的熱導率差異較大時，采用并聯模型計算較為準確，且隨著體積含量的增加，纖維熱導率增加，直到平衡。隨加熱功率和測試時間的增大，復合體系的熱導率增大。

瞬變平面熱源法； 纖維； 熱導率； 并聯模型

單纖維熱導率是纖維集合體熱學性能的基礎，明確纖維熱導率對開發具有特殊傳熱效果的新型紡織品、特種功能織物、復合材料及接觸冷暖感紡織品等具有顯著意義。目前，集中于對纖維集合體導熱性能的研究，如絮片、面料的隔熱性[1-2]，纖維集合體的比熱容和熱導率[3]，被褥、羽絨服[4-6]的保暖性等。單纖維的測試方法分為直接測試法和間接測試法：直接測試是指直接對單纖維熱導率進行測試，如王建立等[7]采用“T”型加熱法測試得到單根碳纖維沿軸向的熱導率為84.35 W/(m·K)；間接測試法是根據對纖維束或復合材料熱導率的測定值，按纖維的體積百分數含量換算而得，如王青利等[3]采用瞬態熱線法測試了北極熊毛纖維束垂直軸向的熱導率范圍為0.027 85～0.054 64 W/(m·K)。目前對單纖維的測試存在以下2個問題：一是由于單纖維長徑比很大，直徑很小(在100 μm以下)，因此對單根纖維熱導率的直接測試很難實現；二是如何測試獲得同種單纖維的軸向和徑向的熱導率，是需要重點考慮的問題。

瞬變平面熱源測試法(TPS)是研究熱傳導性能的一種全新技術。基于TPS原理的Hot Disk熱常數分析儀已被用來測試各種不同材料，比如織物、金屬、礦石、陶瓷、玻璃、粉末、液體等[8]，但截至目前為止，還沒有人采用TPS法測試單纖維軸向及徑向熱導率。本文基于Hot Disk熱常數分析儀的測試系統，分析其測試原理、瞬態平面加熱探頭的傳熱方向等，提出符合測試纖維的軸向和徑向熱導率樣品的制備方法。基于兩相復合介質等效熱導率的物理模型，分別測試了常見纖維的熱導率，與現有數據進行對比，驗證了采用TPS法測試纖維熱導率的可行性，并探討了制樣參數和儀器變量對熱導率測試結果的影響。

1 TPS法的測試原理和方法

1.1 測試原理

Hot Disk熱常數分析儀是通過Hot Disk探頭給最初等溫的樣品提供恒定的功率，在有限的加熱時間里把探頭作為電阻溫度計同時記錄溫度的升高。溫度的動態升高反映在探頭的電阻升高，這個過程被準確地記錄下來，加以分析。由此，熱導率和熱擴散率可通過單次的瞬態記錄被計算出來，并通過如下理論計算得到樣品的軸向和徑向的熱導率。

當Hot Disk通過電流加熱，電阻升高隨時間的方程為

R(t)=R0[1+A(△Ti+△Tave(τ))]

(1)

式中：R0為探頭被加熱前或者t=0時的電阻；A為電阻溫度系數(TCR)；△Ti為覆蓋Hot Disk探頭材料(鎳)絕緣薄層的溫度差分；△Tave(τ)是樣品表面絕緣層另一面與面對Hot Disk探頭(雙螺旋)一面的溫度升高。

隨探頭溫度的升高，樣品表面的溫度也隨之升高，△Ti在極短時間△ti后變為常數，可做以下估計。

(2)

式中：δ為絕緣層厚度；κi為絕緣層材料的熱擴散系數。基于時間的溫度升高由下式給出。

(3)

式中:P0為探頭功率總輸出；α為探頭盤的半徑；Λ為測試樣品的熱導率；D(τ)為與尺寸無關的時間依賴方程。其中

(4)

方程中：t為瞬態記錄開始的時間測量值，而Θ為特征時間，定義為

(5)

式中κ為樣品的熱擴散系數。

利用已記錄的溫度升高來計算曲線D(τ)，通過擬合得到可計算熱導率的最終直線，因此，通過一次瞬態記錄便可得到熱導率和熱擴散系數。

1.2 計算方法

將纖維-環氧樹脂兩相復合體系等效為最簡單且有效的模型：兩相并聯模型和兩相串聯模型[9-10]。假設2組分分別為組分1和組分2，其中，V1為組分1的體積與樣品總體積的比值。

兩相并聯模型中，假設該模型的熱導率為λb，組分1的熱導率為λ1、組分2的熱導率為λ2，則有

λb=λ2[(λ1/λ2-1)V1+1]

(6)

用兩相并聯模型等效樣品中纖維軸向的熱導率，將組分1、2分別視為纖維、樹脂材料，計算得出單纖維軸向的等效熱導率。

由公式(6)可知，當λ1遠遠大于λ2時，λ1/λ2-1將遠大于0，此時，體積比的改變將對計算結果影響顯著，隨體積比的增加，等效熱導率增大，增加幅度大。當λ1/λ2等于1時，體積含量對計算結果沒有影響；當λ1/λ2遠小于1時，隨體積比的增加，等效熱導率增大，但增加幅度小。

在兩相串聯模型中，假設該模型的熱導率為λt，則有

λt=λ2{1/[(λ2/λ1-1)V1+1]}

(7)

用純串聯模型等效樣品中纖維徑向的熱導率，將組分1、2分別視為纖維、樹脂材料，計算得出單纖維徑向的等效熱導率。

1.3 測試方法

首先，要測試樣品的體積比熱。然后，將2個相同尺寸的樣品分別放置在探頭兩端，測試樣品的熱導率。其中，TPS探頭置于2個樣品中間，且上下兩端施加一定的壓力，以減少探頭與樣品之間的空隙。樣品放置、固定好之后用圓筒罩蓋上，以避免空氣流對樣品溫度的干擾。圖1示出了探頭與樣品的位置關系。

本文實驗采用各向異性模塊，當探頭放置于2個相同樣品之間時，探頭釋放的熱量均衡地向周圍擴散，系統會記錄沿著纖維軸向和徑向2個方向的電阻(溫度)增加與時間的關系，得到軸向、徑向不同方向的實驗參數，由此，熱導率和熱擴散系數可通過單次的瞬態記錄被計算出來。

2 實驗部分

2.1 樣品的制備及參數

在一定內徑(18 mm)的模具內，使待測纖維處于豎直平行狀態填充其中。將環氧樹脂與固化劑按一定配比獲得的溶液攪拌均勻，并抽真空處理，以消除所配溶液中的小氣泡。對樣品用真空泵從下往上抽取所配溶液進行灌注，使樣品中的空氣排除干凈。常溫(避免熱處理過程對結果的影響)下放置2 d即可固化，待固化后切成實驗所需的規格尺寸，保證切面的平整，緊接著去除外面的模具殼，即樣品制備完成。圖2示出纖維束固化樣品理論模型的示意圖。

每個樣品均制備2種形式，分別用于測試比熱容和熱導率，2種形式的樣品均為圓柱形，直徑為18 mm，且同種纖維樣品(比熱模塊和導熱模塊)的樹脂和纖維含量及制備過程完全相同，但是試樣厚度存在差異。其中，比熱容的模塊樣品尺寸為：厚度5 mm，直徑18 mm，圖3示出比熱容模塊固化樣品圖。本文實驗選擇5465號探頭(探頭半徑α=3.189 mm)，導熱模塊樣品尺寸要求如下：厚度≥3.826 8 mm，直徑≥7.653 6 mm。導熱模塊樣品實際規格大小：厚度為18 mm；直徑為18 mm，圖4示出熱導率模塊固化樣品圖。

將聚乙烯(PE)纖維、錦綸(PA)、滌綸(PET)、丙綸(PP)、聚乙烯(PE)魚線等纖維經樹脂固化制得測試樣品，通過式(6)、(7)計算得出單纖維的等效熱導率。不同種類纖維的樣品參數如表1所示，PE纖維樣品不同體積比的樣品參數如表2所示。

表1 不同種類纖維樣品基本性能參數Tab.1 Basic performance parameters of different types of fiber samples

表2 PE纖維不同體積比的樣品參數Tab.2 Sample parameters of PE fiber with different volume ratio

2.2 實驗條件

本文實驗在恒溫恒濕環境中進行，測試溫度為室溫，濕度為65%。數據采集時，溫升為0.3 K至3～4 K，1 K左右最好；特征時間在0.3～1 s范圍內；平均偏差在10-3以下。

2.3 空白實驗及結果計算

測試樣品比熱時應先測試參照樣品，加熱功率為120 mW，測試時間為40 s，參照電阻為6.776 0 Ω，樣品溫度為20 ℃，探頭的電阻溫度系數為0.004 7 K-1。空白純樹脂對比樣的纖維體積比為0，將純樹脂對比樣視為各向同性材料。經測試，空白樣的體積比熱為1.339 1 MJ/(m3·K)，熱導率為0.239 5 W/(m·K)。

等效模型中組分2為樹脂，即樹脂的熱導率用λ2表示，樣品軸向熱導率為λb，徑向熱導率為λt。為區分計算出的纖維軸向、徑向等效熱導率，故將式(6)、(7)中的λ1用λ1b、λ1t來表示。在V1已知的條件下，根據公式(6)、(7)分別計算得出纖維軸向等效熱導率(λ1b)和纖維徑向等效熱導率(λ1t)。

3 結果及討論

3.1 不同纖維種類的比熱容和熱導率

表3示出不同纖維種類復合體樣品的比熱模塊結果。由表可知，各樣品比熱差異不大，測試時，加熱功率為120 mW，測量時間為40 s，因此溫度升高都為2.31 K，探頭電阻基本為定值。

表3 不同纖維種類復合體樣品的比熱模塊Tab.3 Specific heat module for samples of different fiber types

注：表中試樣的溫度升高均為2.31 K。

表4示出PE纖維樣品的熱導率，根據式(6)、(7)計算得到纖維等效熱導率。

表4 PE纖維的熱導率模塊結果Tab.4 Thermal conductivity rate of PE fiber

文獻[11]中滌綸的熱導率λ為0.084 W/(m·K)，軸向熱導率為0.974 5 W/(m·K)，徑向熱導率為0.192 1 W/(m·K)，而本文實驗得出滌綸單纖維軸向熱導率為0.972 8 W/(m·K)，徑向熱導率為0.120 6 W/(m·K)，可看出采用并聯模型計算得到的數據差距很小，而采用串聯模型計算出來的徑向熱導率差異較大。

3.2 纖維的體積含量對熱導率的影響

表5示出同種纖維不同體積比的比熱模塊結果。實驗加熱功率為120 mW，測量時間為40 s。由數據可得出，隨著纖維所占體積比的增加，其比熱容逐漸增大。表6示出同種纖維不同體積比的熱導率模塊測試結果。由表可看出，對于同一種纖維而言，隨著纖維填充體積的逐漸增加，纖維的軸向和徑向的熱導率逐漸增加。其中，軸向熱導率變化較大，當含量超過一半后，軸向熱導率的變化趨緩，因此，為了測試的準確性，纖維體積必須達到一定的含量。由于纖維徑向熱導率和樹脂熱導率差異較小，所以，徑向熱導率隨體積含量的增加，數據變化相對較小。

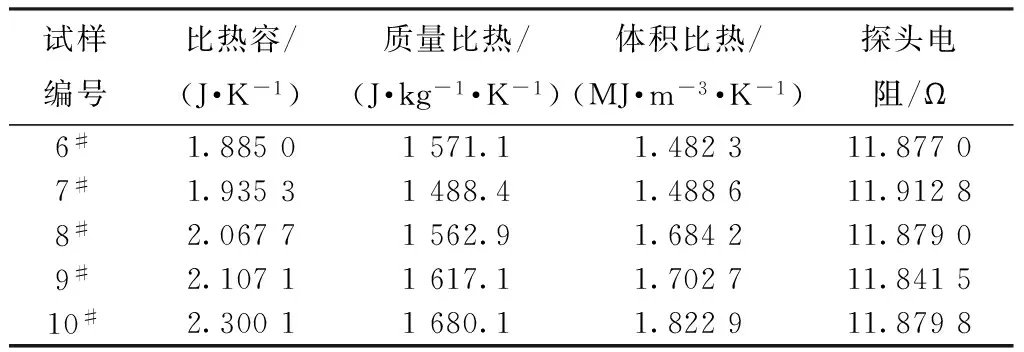
表5 同種纖維不同體積比的比熱模塊結果Tab.5 Thermal module of fiber with different volume ratio

注：表中試樣的溫度升高均為2.31 K。

表6 同種纖維不同體積比的熱導率模塊Tab.6 Thermal conductivity module of fibers with different volume ratio

3.3 串并聯模型對熱導率的影響

單纖維沿軸向、徑向的熱導率是通過測試纖維-環氧樹脂兩相復合體的熱導率，基于等效串并聯模型計算得到的。當等效模型中2組分的熱導率相差(λ1/λ2)很大時，纖維的排列方向和體積比會顯得尤為重要。例如當λ1/λ2=100時，并聯模型與串聯模型的熱導率要相差25倍[10]。結合實驗計算結果，當差異大時，在體積比較大情況下，采用并聯模型獲得的軸向熱導率更準確。另外，實驗的計算理論模型是假設纖維完全處于豎直平行、均勻分布的理想狀態，并將其等效為純串、并聯的理論模型，但在實際情況下纖維的排列狀態并非理論上的完全理想狀態，會對熱導率的測試結果造成一定的誤差。3.4 加熱功率及測試時間對熱導率的影響

加熱功率和測試時間是測試熱導率的關鍵參數。通常，導熱系數大，輸出功率大，測試時間短；導熱系數小，輸出功率小，測試時間長。

實驗調節參數時，若控制測試時間不變，隨著加熱功率的增大，實驗樣品的熱導率測試數值是不斷增大的；若控制加熱功率不變，隨著測試時間的增加，實驗樣品的熱導率測試數值也是不斷增大的。

3.5 探頭大小對熱導率的影響

熱導率方程的解建立在Hot Disk探頭處于無限大模型的假設上，選擇合適的探頭半徑非常重要。根據實驗樣品的大小來選擇合適的探頭尺寸。探頭的半徑應小于樣品厚度和半徑，即樣品的尺寸越大，可選擇的探頭范圍越寬。本文實驗測試的是固體塊狀的熱導率，若探頭選擇過小，探頭的靈敏度高，有可能超過探頭的導熱上限從而燒毀探頭。若探頭選擇過大，則探頭的靈敏度降低，使得探頭產生的熱量不能完全被實驗樣品吸收，從而影響測試結果的可靠性。

4 結 論

基于對TPS測試原理及探頭傳熱方向的分析，提出適用于測試纖維熱導率的纖維-樹脂兩相結構的制樣方法，結合串并聯等效熱導率物理模型，成功實現了單次測試即可獲得纖維的軸向、徑向熱導率，是測試纖維熱導率的新方法。

1)當纖維的熱導率大于樹脂時，隨著復合體系中纖維體積含量的增加，纖維軸向和徑向的等效熱導率也隨之增加。測試時，需要確定合適的體積含量。

2)當2組分熱導率差異很大時，采用并聯模型得到的軸向熱導率更準確。

3)加熱功率、測試時間對熱導率的測試結果影響顯著。不斷調整參數，使溫度升高和特征時間處于最佳范圍，通過多次測量求取平均值，以得到最佳結果。

由文中實驗分析可知，對于同一種纖維而言，隨著纖維填充體積的逐漸增加，纖維的軸向和徑向熱導率的計算結果逐漸增加。當填充體積超過61.92%之后，增加趨勢變緩，因此，環氧樹脂在兩相復合體系中所占的比例對實驗結果有影響，當樹脂含量少于一半時，實驗結果主要取決于纖維本身的熱導率，受樹脂影響較小，另外，樹脂材料一般為熱絕緣材料，其熱導率很小。當實驗所用樹脂種類不同時，對結果的影響也微乎其微。

FZXB

[1] BEHNKE W P. Thermal protective performance test for clothing[J]. Fire Technology, 1977, 13(1): 6-12.

[2] 黃冬梅, 何松. 空氣層位置對消防戰斗服隔熱性能的影響[J]. 紡織學報, 2015, 36(10): 113-119. HUANG Dongmei, HE Song. Influence of air gap position on heat insulation performance of firefighters′ protective clothing[J]. Journal of Textile Research, 2015, 36(10): 113-119.

[3] 王青利, 謝慧麗, 何吉歡. 北極熊毛纖維的導熱系數[J]. 毛紡科技, 2012(9): 59-64. WANG Qingli, XIE Huili, HE Jihuan. Thermal conductivity of polar bear hair fiber[J]. Wool Textile Journal, 2012(9): 59-64.

[4] 黃翠蓉, 于偉東, 許海葉. 羽絨服保暖性探討[J]. 武漢科技學院學報, 2007(1): 25-29. HUANG Cuirong, YU Weidong, XU Haiye. Down warm discussion[J]. Wuhan Institute of Science and Technology, 2007(1): 25-29.

[5] 孔繁琳, 王如竹, 吳靜怡. 新型保暖服的吸附材料熱特性[J]. 紡織學報, 2005, 26(6): 66-68. KONG Fanlin, WANG Ruzhu, WU Jingyi. Thermal properties of the adsorbent material of a new type of warm-retaining clothes[J]. Journal of Textile Research, 2005, 26(6): 66-68.

[6] 李東平. 服裝材料的保暖性與服裝熱阻之關系[J]. 紡織學報, 1998, 19(5): 292-294. LI Dongping. Relationship of clothing materials and warm clothing thermal resistance[J]. Journal of Textile Research, 1998, 19(5): 292-294.

[7] 王建立, 馬維剛, 張興. 測量單根纖維熱導率的新方法[J]. 工程熱物理學報, 2008(6): 991-994. WANG Jianli, MA Weigang, ZHANG Xing. A new method of single fiber thermal conductivity measure-ment[J]. Journal of Engineering Thermo Physics, 2008(6): 991-994.

[8] YI H. Rapid thermal conductivity measurement with a hot disk sensor[J]. Thermochimica Acta, 2005(436): 122-129.

[9] PROGELHOF R C, THRONE J L, RUETSCH R R, et al. Methods for predicting the thermal conductivity of composite systems: a review[J]. Polymer Engineering and Science, 1976, 16(9): 615-625.

[10] 陳則韶,錢軍,葉一火. 復合材料等效導熱系數的理論推算[J]. 中國科學技術大學學報,1992(4):416-424. CHEN Zeshao, QIAN Jun, YE Yihuo. Composite theoretical calculations of equivalent thermal conductivi-ty[J]. Journal of University of Science and Technology of China, 1992(4): 416-424.

[11] 于偉東.紡織材料學[M].上海:中國紡織大學出版社,2006:140-143. YU Weidong. Textile Materials Science[M]. Shanghai: China Textile University Press, 2006: 140-143.

Testing of thermal conductivity of fiber based on transient plane heat source method

LI Li1,2, XIAO Hong2, CHENG Bowen1, HUAI Xiangbing3

(1.SchoolofTextiles,TianjinPolytechnicUniversity,Tianjin300387,China; 2.TheQuartermasterEquipmentResearchInstituteofLogisticalSupportDepartment,Beijing100010,China; 3.JiangyinHongliuBedSheetCo.,Ltd.,Jiangyin,Jiangsu214432,China)

In order to solve the problem of difficulty in the testing of thermal conductivity of single fiber, based on series-parallel two-phase composite dielectric equivalent thermal conductivity physical model, the paper adopted a transient plane heat source method for testing epoxy resin-fiber composites, and calculated the axial and radial thermal conductivities of single fiber. The results show that this method can achieve the thermal conductivity of fiber, and the fiber axial thermal conductivity is significantly greater than the fiber radial thermal conductivity, verifying the thermal properties anisotropy of the fiber. Effect of thermal conductivity differences in the composite system of two phases, the volume ratio and physical models, instrumentation, heating power, test time, etc. on the fiber thermal conductivity results is significant. When the thermal conductivity of fiber and resin are quite different, the use of parallel computing model is more accurate, and with increasing of volume fraction, the fiber thermal conductivity increases to the balance. With increasing of heating power and test time, the thermal conductivity of the composite system is increased.

transient plane heat source method; fiber ; thermal conductivity; parallel computing model

10.13475/j.fzxb.20160203606

2016-02-28

2016-08-29

國家自然科學基金青年基金項目(51203114)

李麗(1991—)，女，研究生。主要研究方向為纖維及織物的傳熱及熱學性能。肖紅，通信作者，E-mail:76echo@vip.sina.com。

TS 102

A