應用最優Gabor濾波器的經編織物疵點檢測

尉苗苗， 李岳陽， 蔣高明， 叢洪蓮

(江南大學 教育部針織技術工程研究中心， 江蘇 無錫 214122)

應用最優Gabor濾波器的經編織物疵點檢測

尉苗苗， 李岳陽， 蔣高明， 叢洪蓮

(江南大學 教育部針織技術工程研究中心， 江蘇 無錫 214122)

針對經編織物疵點自動檢測問題，提出了一種新的基于最優Gabor濾波器的經編織物疵點檢測方法。具體可分為學習階段和檢測階段；在學習階段，對于無疵點的經編織物圖像構造可調制的二維Gabor濾波器，采用量子行為粒子群優化(QPSO)算法對Gabor濾波器的參數進行優化，得到與無疵點的織物圖像紋理特征最匹配的Gabor濾波器參數；在檢測階段，由學習階段得到的最佳參數構造Gabor濾波器，用該濾波器對待檢測織物圖像進行卷積處理，然后再對得到的卷積圖像進行二值化處理，最終識別出待檢測織物是否有疵點存在。結果表明，該方法的檢測率可以達到96.67%，具有很好的穩定性和魯棒性，適合應用于工業生產。

經編織物疵點檢測； 最優Gabor濾波器； 量子行為粒子群優化算法； 圖像分割

經編機生產過程中，紗線斷裂后織物會出現疵點，目前很多紡織企業的疵點檢測都是由人工完成的，但人工檢測存在諸多不足[1]：由于檢測疵點是一種重復性的任務，而且需要注意力高度集中，檢測工人很容易疲勞厭煩，準確率僅可以達到60%～70%；人工檢測花費的成本較高，需要雇傭一大批工人不間斷地進行檢測。

近年來基于機器視覺和圖像處理的織物疵點檢測方法大量涌現，主要分為3類方法[2-3]：基于統計的方法[4]、基于頻域的方法、基于模型的方法[5]。在這些方法當中，利用Gabor濾波器對織物圖像進行分析主要可分為2類[6]：多尺度多方向的Gabor濾波器組[7]；可以調制的Gabor濾波器[8]。濾波器組的方法需要預先設定好一組參數，這組參數可以構造出一組Gabor濾波器，這組濾波器需要包含整個特征空間，這種方法可以有效地進行疵點區域與無疵點區域的分割，但是最大的弊端就是需要多個濾波器，計算量大，沒有很強的實時性，應用于工業生產受到了限制。可以調制的Gabor濾波器方法通過最優化方法調整一個濾波器的參數，使其與無疵點的背景圖像紋理特征相適應，得到最適應背景圖像紋理特征的濾波器參數后，構造單個Gabor濾波器對織物圖像進行檢測。這種方法，在保證檢測正確率的前提下，盡可能減少運算時間，實時性強，更適合應用于工業生產當中。

本文方法屬于可以調制的Gabor濾波器的方法。很多研究者已經對最優Gabor濾波器的設計進行了研究，分別采用遺傳算法[9]和模擬退火算法[10]等。對于最優化Gabor濾波器的方法，關鍵問題是采用有效的最優化算法選擇最優參數,才能更容易應用于工業生產。基于此，本文采用量子行為粒子群優化(QPSO)算法作為選取最優Gabor濾波器參數的方法，該方法根據Fisher準則[11]構造一個目標函數，建立一個非線性規劃問題的數學模型，利用QPSO算法求解該模型就可以得到最佳Gabor濾波器的參數，該方法能有效地提取出Gabor濾波器的最優參數。

1 二維Gabor濾波器

在空間域中，二維Gabor濾波器[12-13]是由方向性復正弦函數調諧的二維Gaussian核函數調制而成，空間域中二維Gabor濾波器可以表示為

G(x,y)=g(x′,y′)exp(2πj(Ux′+Vy′))

(1)

式中：x′=xcosθ+ysinθ，y′=-xsinθ+ycosθ；θ為旋轉角度；U是x軸方向的頻率；V是y軸方向的頻率；g(x′,y′)是二維Gaussian 核函數。式(1)中二維Gaussian核函數g(x′,y′)的表達式為

(2)

式中：δx為Gaussian核函數x軸方向上的尺度參數；δy為Gaussian核函數y軸方向上的尺度參數。

Gabor濾波器是由Gaussian核函數乘以復正弦函數得到的,可表示為

G(x,y)=Ge(x,y)+jGo(x,y)

(3)

式中：Ge(x,y)是二維Gabor濾波器的實部；Go(x,y)是二維Gabor濾波器的虛部。

圖像經過Gabor卷積后的圖像R(x,y)可以表示為

R(x,y)=T(x,y)*G(x,y)

(4)

式中：T(x,y)是無疵點的經編織物圖像；R(x,y)是經過Gabor濾波器卷積后的圖像；*是圖像的卷積操作。

Gabor濾波函數經過適當的膨脹收縮或旋轉，可以得到自相似的不同方向不同尺度的Gabor濾波函數，1個Gabor濾波器由1組參數Φ=(δx,δy,U,V,θ)決定，Φ作為Gabor濾波器提取的參數用于最優Gabor濾波器的選取。

2 疵點檢測算法

2.1 疵點檢測算法的主要步驟

本文提出的織物疵點檢測方法可以視為2種紋理的圖像分割法[14-15],有疵點的區域和無疵點的區域紋理特征上有差異，含有疵點的織物圖像最少包含2種紋理,分割不同紋理即可檢測出疵點位置。對于一種織物圖像，正常織物的紋理特征是類似的，不同種類的疵點的紋理特征是多種多樣的，同一種疵點紋理特征也有個體差異，學習所有疵點種類的紋理特征是不切實際的，所以只學習正常織物紋理的特征。本文采用半監督的方式[6]，將這些紋理特征作為檢測疵點的依據。

圖1示出織物疵點的檢測流程圖。本文的織物疵點檢測方法主要分為2個階段。學習階段：對N×N的無疵點經編織物圖像T(x,y)，構造出二維Gabor濾波器G(x,y)，提取出Gabor濾波參數Φ=(δx,δy,U,V,θ)。根據Fisher準則構造出目標函數，然后建立具有5個決策變量、3個約束條件的非線性規劃問題的數學模型，再利用量子行為粒子群優化(QPSO)算法對提取出來的Gabor濾波參數進行最優化處理，得到Gabor濾波器的最優參數Φ*。檢測階段：根據學習階段獲取的參數Φ*建立Gabor濾波器，對待檢測織物圖像S(x,y)進行Gabor卷積處理，再采用低通Gabor濾波器對卷積后的圖像進行卷積，降低毛刺信號的干擾，然后再采用中值濾波對卷積后的圖像做進一步的平滑處理，最后進行閾值分割得到疵點檢測結果。

2.2 目標函數

本文采用Fisher準則構造目標函數作為QPSO算法的適應度函數。Fisher準則已經廣泛地應用于模式識別領域，并且成功地解決了2種紋理的圖像分割問題[14-15]。圖像分割目的是對2種已知的紋理進行分割，已知2種紋理圖像I1(x，y)，I2(x，y)，相應的Fisher準則的代價函數可以表示為

(5)

對于織物疵點檢測問題也可以視為2種紋理的圖像分割，即為已知的無疵點的背景圖像區域和未知的有疵點的圖像區域。由于僅對無疵點的背景圖像紋理特征已知，根據式(5)構造出最優化問題的目標函數為

(6)

式中：Gabor濾波器的參數Φ=(δx,δy,U,V,θ)；μ(Φ)和σ(Φ)分別是經編織物圖像經過Gabor卷積后的能量均值和標準差。

μ(Φ)和σ(Φ)可以分別表示為

(7)

(8)

式中Gabor卷積后的圖像其能量Er(x,y)可以表示為

Er(x,y)=[(T(x,y)*Ge(x,y))2+

(9)

在特定的解空間內，要找到與無疵點的織物圖像T(x，y)紋理特征相匹配的Gabor濾波器參數，需要使能量響應值的均值μ(Φ)達到最大，并且使其方差σ(Φ)達到最小，也就是使目標函數F(Φ)達到最小，這樣就能夠得到最優Gabor濾波參數Φ*。

2.3 建立優化問題模型

本文上述的經編織物疵點檢測的優化模型可以建立為具有5個決策變量、3個約束條件的非線性規劃問題，具體可以描述為

(10)

其中，限制條件式1表示Gabor濾波器的尺度范圍，保證最大的Gabor濾波器在被卷積的圖像內部；限制條件式2是Gabor濾波器中心(U,V)的取值范圍,上限是Nyquist frequency (0.5cycles/pixel)的一半；考慮到Gabor濾波器的對稱性，限制條件式3中旋轉角度范圍從0到π。

2.4 QPSO算法求解優化問題模型

對于本文提出的織物疵點檢測優化模型采用QPSO算法進行優化。QPSO算法是在粒子群優化(PSO)算法的基礎上，發現人類的學習過程與粒子的量子行為極為相似而開發的群體智能算法。QPSO算法參數較少，隨機性強，收斂速度快，能覆蓋整個解空間具有非常好的全局搜索能力，已經成功應用在諸多領域。本文采用QPSO算法對式(10)建立的非線性規劃模型進行參數優化，具體按照如下步驟：

1)初始化粒子群，包括確定最大迭代次數、搜索空間、粒子的個數、隨機初始化粒子的位置(即為Gabor濾波器參數Φ的一組值)。

設初始時迭代次數n=0，最大迭代次數為max_n；需要確定最優值的參數有Φ=(δx,δy,U,V,θ)，則搜索空間為5維；群體由M個粒子組成x={x1,x2,…,xM}，其中第i個粒子位置為

(11)

個體最好位置為

(12)

群體的全局最好位置為

(13)

其中i=1,2,…,M。

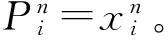
(14)

3)每個粒子位置的更新，也就是Gabor濾波器參數的動態調整過程，采用與步驟2相同方法求出每個粒子的適應度函數值，更新個體最好位置和全局最好位置。

由QPSO算法，粒子的位置更新方程為

(15)

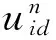
(16)

(17)

每個粒子的位置更新后，采用與步驟2)相同方法求出每個粒子的適應度函數值，然后由式(18)更新個體最好位置：

(18)

由上式得到每個粒子個體最好位置保存的是到當前為止具有最小適應度函數值的位置。

每個粒子的個體最好位置確定后，就可根據式(14)更新全局最好位置。

4)訓練在滿足迭代結束條件時結束，全局最好位置即為所要確定的Gabor濾波參數的一組最優值；否則，迭代次數加1，轉到步驟3)。

迭代結束條件一般是迭代次數n等于max_n。

2.5 閾值分割濾波后的圖像

根據學習過程中得到的最優Gabor濾波器參數Φ*，構造出單個Gabor濾波器。由式(4)用構造出來的濾波器與待檢測的經編織物圖像S(x,y)進行卷積操作，得到卷積后的圖像S′(x,y)。圖2示出含有斷經疵點的經編織物圖像，經過最優Gabor濾波器卷積操作后，圖像能量響應值的三維視圖，可以看出卷積后的圖像毛刺信號較強。

在閾值分割得到二值化檢測結果前需要進一步對圖像做平滑處理，具體按照如下步驟。

1)經過最優Gabor濾波器卷積后的圖像S′(x,y)中含有大量的噪聲，文獻[11]采用11像素×11像素的低通Gaussian濾波器再次對卷積后的圖像S′(x,y)進行卷積處理，這樣可以減少噪聲斑點對二值化過程的影響，但是使用Gaussian濾波器效果改善并不是很明顯，本文采用一個低通Gabor濾波器再次對卷積后的圖像S′(x,y)進行卷積操作，得到卷積后的圖像S″(x,y)，再次經過低通Gabor濾波器卷積的圖像能量響應值三維視圖如圖3所示，毛刺信號比圖2明顯減弱。

2)經過2次Gabor濾波器卷積后的圖像S″(x,y)繼續采用21像素×21像素的中值濾波器進行卷積處理，得到卷積后的圖像S?(x,y)，濾波后的圖像能量響應值的三維視圖如圖4所示。無疵點的區域和有疵點的區域圖像能量響應值差別更加明顯，并且毛刺信號進一步減弱。

對經過上述處理的圖像S?(x,y)做閾值分割處理，由式(9)可計算得到每個像素位置的能量響應值Er(x,y)。再由式(19)進行閾值分割處理：

(19)

式中：B(x,y)是二值圖像，根據式(7)、(8)，μ是經過上述處理后圖像的能量均值；σ是能量標準差；c是一個實驗常數，由實驗得到；B(x,y)就是疵點檢測的最終結果，由B(x,y)來判斷是否含有疵點。若B(x,y)的值為1，則待檢測圖像相對應的像素位置有疵點；若B(x,y)的值為0，則待檢測圖像相對應的像素位置無疵點。

3 實驗與分析

3.1 與經典算法檢測效果對比

為了檢驗本文提出的疵點檢測算法的效果，收集了60幅經編織物圖像，參照GB/T 17759—2009《本色布布面疵點檢測方法》對收集到的圖像進行分類和統計。離線數據庫中包含20張無疵點的樣本，40張不同種類的疵點樣本，所有的樣本都是512像素×512像素8位的灰度圖像。實驗采用Intel OpenCV 2.4.9計算機視覺方法庫，在Microsoft Visual Studio 2010平臺上進行。為了驗證本文提出算法的有效性，對文獻[7]的經典算法與本文提出的算法在相同的數據庫上的檢測效果進行比較，文獻[7]采用Gabor濾波器組，需要使用不同尺度不同方向的一組Gabor濾波器，而本文算法利用QPSO算法訓練Gabor濾波器參數，檢測時使用構造的單個最優Gabor濾波器，檢測效率明顯優于前者。算法檢測效果的評價用二值化圖像表明，檢測結果如圖5所示。數據庫整體檢測結果見表1、2。表2中正檢率表示包含疵點的圖像可以被正確檢測的比率，誤檢率表示不含疵點的圖像被誤認為包含疵點的比率。

表1 疵點檢測結果統計
Tab.1 Statistics for defect detection results

方法輸入圖像檢測結果/張檢測出未檢測出本文方法包含疵點382不含疵點200文獻[7]方法包含疵點364不含疵點173

檢測結果表明文獻[7]和本文算法都能將疵點檢測出來，而圖5(d)、(e)、(f)更清晰、更準確，從而證明了本文算法的有效性。

分析表1、2經編織物圖像疵點檢測結果統計表

表2 疵點檢測率統計Tab.2 Percent efficiency of proposed method

可知，本文算法對于包含疵點的經編織物圖像正檢率較高，對不包含疵點的經編織物圖像誤檢率較低，從而證明了本文算法在穩定性上優于文獻[7]的經典算法。

3.2 與最新算法參數學習效率對比

為了檢驗本文算法的最優Gabor濾波器參數學習效率，實驗收集了256像素×256像素、128像素×128像素、64像素×64像素無疵點經編織物圖像樣本，對文獻[8]的算法參數學習效率與本文算法參數學習效率作對比，文獻[8]采用遺傳算法對二維Gabor濾波器做最優化處理。

在保證能夠獲取足夠無疵點圖像紋理特征信息的前提下，學習階段所使用的無疵點經編織物圖像T(x,y)的像素尺寸越小，所需的學習時間越少，文獻[8]中證明了當T(x,y)的尺寸大于或等于64像素×64像素，所獲得的最優Gabor濾波器可以包含足夠的紋理特征信息，因此，本文采用的樣本尺寸大于或等于64像素×64像素。表3統計了本文算法和文獻[8]算法在參數學習上所需要的時間，顯然本文算法在參數學習效率方面要優于文獻[8]的算法，尤其是在T(x,y)的尺寸較大時，參數學習效率差距明顯，從而證明了本文算法參數學習效率更優。

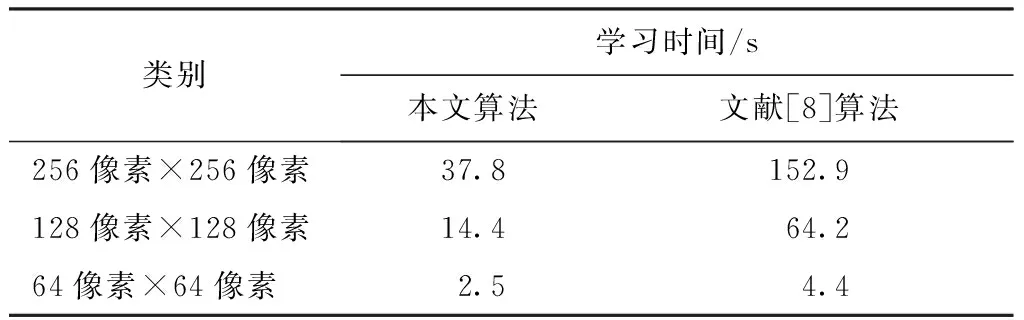
表3 學習效率統計Tab.3 Statistics for learning efficiency

3.3 工業生產應用

為了進一步檢驗本文算法的有效性，將本文算法應用到實際生產過程中。采用MicroView公司生產的線陣CCD工業相機(MVC2048DLM-GE19-SOO)，日本理光公司生產的35 mm焦距鏡頭(FL-YFL3528)，在卡爾邁耶公司生產的KS4 EL型電子橫移高速經編機上進行實驗。在正常運行的經編機出布口處實時采集分辨率為1028像素×128像素的經編織物灰度圖像。采用本文算法對其進行檢測，結果如圖6所示。斷經疵點被成功地檢測出來，盡管圖像有輕微的像素平移，疵點仍然能被準確地檢測出來。

如圖6(a)所示，在紗線剛斷的時刻，紗線張力發生改變，但是仍然有殘留的紗線纏繞其中，此時所形成的疵點并不是很明顯。圖6(b)的檢測結果證明了本文疵點檢測算法可以有效地檢測出剛開始形成的疵點，這對于工業生產中布匹疵點的控制非常重要，發現疵點后立即停車，以減少疵點對布匹質量的影響。圖6(b)、(d)示出清晰的檢測結果，進一步證明了本文算法的有效性、穩定性以及魯棒性。

4 結 論

本文主要針對經編織物斷經、油污、破洞等疵點的檢測方法進行研究。采用半監督的方式，對無疵點的經編織物圖像，利用QPSO算法訓練Gabor濾波器參數，檢測時使用構造的單個最優Gabor濾波器，相比使用濾波器組的經典算法，能夠更有效地、準確地檢測經編織物疵點，更有利用于工業生產。目標函數通過Fisher準則構造，使得學習過程獲得的最佳參數構造的Gabor濾波器與無疵點的織物圖像紋理更加契合，從而使構造出的Gabor濾波器更有效地檢測經編織物疵點。實驗結果證明了本文算法的有效性，穩定性和魯棒性。

FZXB

[1] CHO C S, CHUNG B M, PARK M J. Development of real-time vision-based fabric inspection system [J]. IEEE Transactions on Industrial Electronics, 2005, 52(4): 1073-1079.

[2] KUMAR A. Computer-vision-based fabric defect detection: a survey [J]. IEEE Transactions on Industrial Electronics, 2008, 55 (1): 348-363.

[3] NGAN H Y T, PANG G K H, YUNG N H C. Automated fabric defect detection: a review [J]. Image and Vision Computing, 2011, 29 (7): 442-458.

[4] SHI M H, FU R, GUO Y, et al. Fabric defect detection using local contrast deviations [J]. Multimedia Tools and Applications, 2011, 52 (1): 147-157.

[5] CAMPBELL J G, FRALEY C, MURTAGH F, et al. Linear flaw detection in woven textiles using model-based clustering [J]. Pattern Recognition Letters, 1997, 18 (14): 1539-1548.

[6] BODNAROVA A, BENNAMOUN M, LATHAM S. Optimal Gabor filters for textile flaw detection [J]. Pattern Recognition, 2002, 35 (12): 2973-2991.

[7] KUMAR A, PANG G K H. Defect detection in textured materials using gabor filters [J]. IEEE Transactions on Industry Applications, 2002, 38 (2): 425-440.

[8] HU Guanghua. Automated defect detection in textured surfaces using optimal elliptical Gabor filters [J]. Optik, 2015, 126 (14): 1331-1340.

[9] JING J F, YANG P P, LI P F, et al. Supervised defect detection on textile fabrics via optimal Gabor filter [J]. Journal of Industrial Textiles, 2014, 44 (1): 40-57.

[10] HU Guanghua. Optimal ring Gabor filter design for texture defect detection using a simulated annealing algorithm [C]// Information Science. Shanghai: Electronics and Electrical Engineering (ISEEE), 2014: 860-864.

[11] KUMAR A, PANG G K H. Defect detection in textured materials using optimized filters [J]. IEEE Transactions on Systems Man and Cybernetics Part B-Cybernetics, 2002, 32 (5): 553-570.

[12] DAUGMAN J G. Uncertainty relation for resolution in space, spatial frequency, and orientation optimized by two-dimensional visual cortical filters [J]. Journal of the Optical Society of America. A, Optics and Image Science, 1985, 2 (7): 1160-9.

[13] GABOR D. Theory of communication[J]. Electrical Engineers Part III: Radio and Communication Engineering, 1946, 93 (26): 429-457.

[14] DUNN D, HIGGINS W E. Optimal Gabor filters for texture segmentation [J]. IEEE Transactions on Image Processing, 1995, 4 (7): 947-964.

[15] TSAI D M, WU S K, CHEN M C. Optimal Gabor filter design for texture segmentation using stochastic optimization [J]. Image and Vision Computing, 2001, 19 (5): 299-316.

Warp knit fabric defect detection method based on optimal Gabor filter

YU Miaomiao, LI Yueyang, JIANG Gaoming, CONG Honglian

(Engineering Research Center for Knitting Technology, Ministry of Education, Jiangnan University, Wuxi, Jiangsu 214122, China)

Focusing on automatic image inspection of warp knit fabric defects in textile industry, a new method for warp knit fabric defect detection based on an optimal Gabor filter is presented. The proposed method consists of two processes: the training process and the inspection process. In the training process, the parameters of the 2-D Gabor filter can be tuned by the quantum-behaved particle swarm optimization (QPSO) algorithm to match with the texture features of a defect-free template acquired in prior. In the inspection process, each sample fabric image under inspection is convoluted with the selected optimized Gabor filter. Then a simple thresholding scheme is applied to generate a binary segmented result. Experimental results show that the detection rate of the proposed method can reach 96.67%. It has good performance of stability and robustness, suitable for industrial production.

warp knit fabric defect detection； optimal Gabor filter； quantum-behaved particle swarm optimization algorithm； image segmentation

10.13475/j.fzxb.20151101107

2015-11-03

2016-03-29

江蘇省產學研聯合創新資金-前瞻性聯合研究項目(BY2015019-11)；中央高校基本科研業務費專項資金項目(JUSRP51404A，JUSRP211A38)；江蘇高校優勢學科建設工程資助項目(蘇政辦(2014)37號)

尉苗苗(1988—)，男，碩士生。主要研究方向為圖像處理在針織上的應用。李岳陽，通信作者，E-mail： lyueyang@jiangnan.edu.cn。

TP 391.41

A