靜電陀螺監控器對航天器定軌精度影響分析

周海淵，王旭良，李紅艷，楊 恒

（中國衛星海上測控部，江陰 214431）

靜電陀螺監控器對航天器定軌精度影響分析

周海淵，王旭良，李紅艷，楊 恒

（中國衛星海上測控部，江陰 214431）

航天測量船與陸基測控站在對航天器進行軌道跟蹤測量中存在很大區別，陸基測控站是定點測控，定軌精度完全取決于無線電設備自身精度，而測量船是海基動態測控，定軌精度除受無線電設備自身精度影響，更大程度上受制于慣性導航系統（INS）提供的船姿船位(航向、船搖、位置)數據精度。測量船為提高船姿船位數據精度，使用了靜電陀螺監控器（ESGM）與慣性導航設備（INS）、全球衛星導航系統（GNSS）相結合的組合導航系統。結合 INS/ESGM/GNSS工作原理和測量船航天器定軌中船姿船位數據源的選擇，將船姿船位數據精度對測量船定軌精度的影響進行了仿真，并通過無線電設備實測數據的事后數據處理對仿真結果進行了驗證。研究結果表明，ESGM能夠在很大程度上提高測量船航天器的定軌精度。

靜電陀螺監控器；組合導航；數據仿真；定軌精度

測量船由于測量點位的靈活性和測控覆蓋范圍的廣泛性，早已成為我國航天測控網不可或缺的重要組成部分。但是由于海基測量是在動態條件下進行，測量船船姿船位都在實時變化，導致海基測控定軌精度一般而言不如陸基測控站[1-3]。然而軌道確定是航天器測量、控制和應用的基礎，因此如何提高測量船船姿船位數據精度成為測量船海基測量的關鍵所在[4-5]。

為提高海基航天器測控定軌精度，第三代航天測量船配備了以ESGM設備為核心的INS/ESGM/ GNSS組合導航系統[7-8]。本文從該組合導航系統工作原理出發，結合海基測控航天器定軌中船姿船位數據源的使用原則，從仿真數據和實測數據兩個方面研究了船姿船位數據誤差對航天器定軌精度的影響，最后將應用ESGM前后測量船的航天器定軌精度進行了比較。

1 組合導航系統的構成及工作原理

ESGM/INS/GNSS組合導航系統結構如圖1所示。其工作原理進行如下：ESGM連續實時地接收INS的位置（經度λ、緯度φ）、姿態（橫搖R、縱搖P）、航向（K）等信息，并向INS輸出位置和航向的修正量，以保證INS能夠長時間、高精度的工作；全球導航衛星系統（GNSS）為INS和ESGM實時提供精確的位置信息，是INS和ESGM校準的位置比對基準。

該系統圖中的標校經緯儀（CNS）是測量船航向的基準。由于光學系統的高精度特性，CNS接收INS位置和姿態數據后可以利用天文導航計算出INS的航向誤差進而對INS航向進行修正，同時ESGM的航向精度也需要利用經緯儀進行檢測驗證。CNS/INS/GNSS是在ESGM應用之前測量船常用的組合導航系統。

圖1 ESGM/INS/GNSS組合導航系統工作原理Fig.1 Principle of ESGM/INS/GNSS integrated navigation system

2 海基定軌誤差來源分析

在未裝備ESGM設備之前，測量船一般在測控任務開始之前15 min使用CNS和GNSS數據完成對INS的最后一次校準；在裝備ESGM之后，ESGM和GNSS實時對INS數據進行校準修正。

在組合導航系統中，位置信息GNSS精度最高，橫搖和縱搖姿態信息只有INS能夠提供，而航向信息的來源有INS、CNS、ESGM這3個，INS航向精度較低，需要CNS和ESGM進行修正。

綜合以上測量船在航天器定軌過程中，船姿船位數據來源如下：經緯度位置數據來源于GNSS數據；橫縱搖數據來源于INS；航向數據來源于ESGM或者CNS。由此得出對于海上測控精度的影響的最關鍵因素就是航向數據的來源與精度。

CNS/INS/GNSS與ESGM/INS/GNSS兩者之間最大區別在于，雖然CNS精度最高，甚至可以在校準后的瞬間使得INS航向誤差幾乎為零，但是在測控任務中，CNS對INS最后一次校準至跟蹤結束，CNS對于INS航向誤差逐漸發散增大的情況卻無能為力，即CNS無法對INS航向進行實時修正。比較而言，ESGM校準INS航向其瞬時精度雖然無法達到CNS水平，卻可以實時對INS航向進行監控和修正。

目前相關數據的誤差如下：GNSS位置測量誤差為0~20 m；INS橫縱搖誤差0"~10"；經過統計INS航向使用CNS修正初始誤差為0"，1 h測控任務跟蹤結束后INS航向誤差一般能夠達到20"~40"，使用ESGM修正從跟蹤開始至結束，INS航向誤差實時能夠保持在10"~20"。

3 海基定軌精度仿真分析

航天器的典型軌道有兩種，一種是近地近圓軌道，另一種是大偏心率軌道。在仿真過程中，分別以兩種典型軌道類型的理論彈道數據為標準數據，并在標準數據上添加各測量設備的測量誤差。各設備疊加的誤差如下：無線電設備測距誤差7 m，測角誤差41.3"，GNSS位置誤差20 m，INS縱橫搖誤差采用5"，CNS和ESGM修正INS航向的誤差取其統計平均值分別取20"和10"。以理論入軌根數為比對標準，采用蒙特卡羅方法模擬100次，并統計定軌結果半長軸誤差的標準差，結果如表1所示。

從仿真結果看：對于近地近圓軌道，使用ESGM對航向數據進行修正，定軌結果半長軸有 20多米改進；而對于超大偏心率軌道，經過ESGM數據修正后，定軌結果半長軸改進比較明顯，半長軸精度提高了20 km以上。因此從理論仿真層面分析可以得到以下結論，使用ESGM能夠提高海上測控定軌精度。

表1 仿真計算半長軸誤差Tab.1 Calculation of major semi-axis error in simulation

4 無線電設備跟蹤精度分析

海基無線電設備通過組合導航系統提供的船姿船位數據對航天器進行測控定軌，即船姿船位數據誤差最終疊加反映在無線電設備的實測數據。根據前面分析，其中的關鍵為航向數據對無線電設備方位精度的影響。不同類型的航向數據對無線電設備跟蹤測量過程中的方位數據有著決定性影響，具體情況可以通過方位殘差反映，方位殘差越小，平均值越趨近于零，定軌精度越高。

圖 2和圖 3分別為兩次海上測控任務分別采用CNS/INS/GNSS與ESGM/INS/GNSS提供的船姿船位數據進行事后數據處理后得到的無線電設備方位殘差，其中圖2為某次近地近圓軌道任務，圖3為某次大偏心率軌道任務。

數據比對的基準采用火箭箭載GPS。比對結果發現，使用CNS/INS/GNSS與ESGM/INS/GNSS船姿船位數據分別計算的無線電設備方位殘差，后者比前者平均值更接近于零，而且殘差減小了約10″。因此從設備層面分析可以得到以下結論：使用ESGM/INS/GNSS無線電設備方位殘差較小，而海上測控無線電設備引入的誤差越小定軌精度更高。

圖2 近地近圓軌道定軌方位殘差Fig.2 Near circular orbit range residuals

圖3 大偏心率軌道定軌方位殘差Fig.3 Highly eccentric orbit range residuals

5 軌道改進結果分析

為了進一步研究ESGM對于測量船航天器定軌結果的具體影響，在此進行了軌道改進結果分析。表 2和表3分別為圖2和圖3所對應的兩次海上測控任務分別采用CNS/INS/GNSS與ESGM/ INS/GNSS船姿船位數據的定軌結果偏差，比對標準為某測控中心事后數據處理的精確軌道。軌道計算方法為三元素單位矢量法。

對軌道改進數據試算結果的分析表明，仿真結果與設備方位殘差反映的情況基本一致。對于近地近圓軌道，航向數據對定軌半長軸有所改進但是影響較小；使用 ESGM數據對航向進行修正后，軌道半長軸能改進20 m左右；而對于超大偏心率軌道，修正航向數據后，對定軌結果半長軸影響比較明顯，軌道半長軸能改進20 km左右。

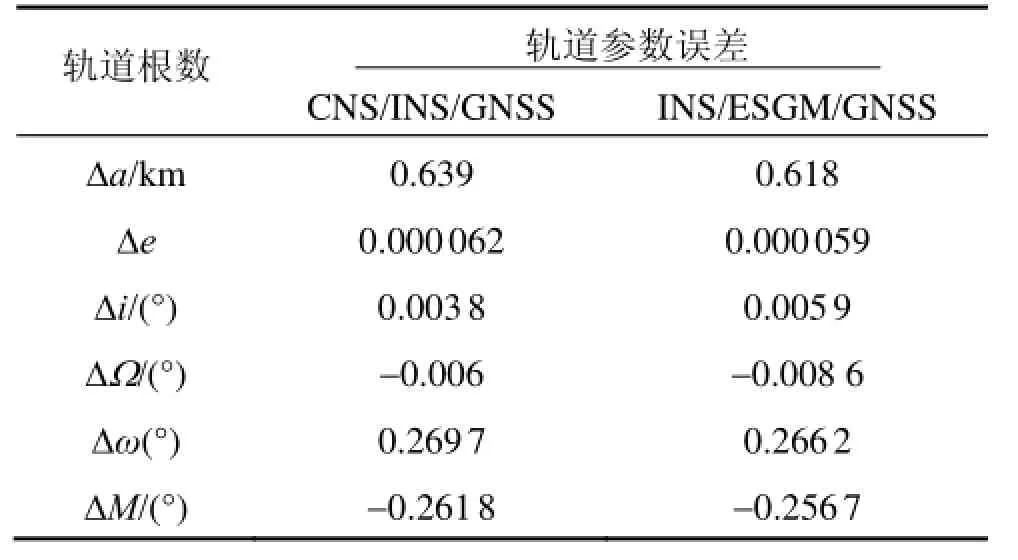
表2 近地近圓軌道定軌結果Tab.2 Determination results of close earth and nearly round orbit

表3 大偏心率軌道定軌結果Tab.3 Determination results of highly eccentric orbit

6 結 論

ESGM的應用極大提高了測量船船姿船位數據精度，對提高海上測控任務定軌精度具有積極作用。本文分析了測量船海上測控任務定軌的誤差來源，進行了軌道改進的數據仿真，利用實測數據的事后數據處理對仿真結果進行了驗證。研究結果表明：使用ESGM可以在一定程度上減小無線電設備的方位殘差，能夠有效提高海上測控任務的定軌精度。

（References）：

[1] 樊士偉, 孟鐵男, 高為廣, 等. 航天器測定軌技術綜述[J]. 測繪科學技術學報, 2013, 30(6): 549-556.

Fan Shi-wei, Meng Tie-nan, Gao Wei-guang, et al. Summarizing on the development of space orbit determination technology[J]. Journal of Geomatics Science and Technology, 2013, 30(6): 549-556.

[2] Tsui J B Y. Fundamentals of global positioning system receivers: a software approach[M]. New York: Wiley & Sons, 2000: 133-164.

[3] AKos D M et al. Low power global navigation satellite system(GNSS) signal detection and processing[C]// Proc. ION GPS 2000. Salt Lake City, UT, 2000: 784-791.

[4] 沐俊山, 劉冰, 薛國虎, 等. 基于測量船的實時定軌改進方法[J]. 電訊技術, 2013, 53(2): 177-181.

Mu Jun-shan, Liu Bing, Xue Guo-hu, et al. Improvement of optimal sequential orbit determination method for TT&C ship[J]. Telecommunication Engineering, 2013, 53(2): 177-181.

[5] 康德勇, 李曉勇, 王旭良. 船位誤差對外彈道測量及定軌精度的影響[J]. 電訊技術, 2010, 50(9): 106-109.

Kang De-yong, Li Xiao-yong, Wang Xu-liang. Influence of ship's position error on exterior trajectory measurement and orbit determination[J]. Telecommunication Engineering, 2010, 50(9): 106-109.

[6] 馮鴻奎, 李曉勇, 薛國虎, 等. 航天測量船導航系統ESGM技術[J]. 飛行器測控學報, 2010, 29(1): 28-33.

Feng Hong-kui, Li Xiao-yong, Xue Guo-hu, et al. Application of ESGM technique on space instrumentation ships[J]. Journal of Spacecraft TT&C Technology, 2010, 29(1): 28-33.

[7] Christensen W. Advanced development of ESG strap down navigation system[J]. IEEE Transactions on Aerospace and Electronic Systems, 1996, 2(2): 143-157.

[8] Zhang Ke-zhi, Tian Wei-feng, Qian Feng. Combination of distributed Kalman filter and BP neural network for ESG bias model identification[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2010, 27(3): 226-231.

Analysis of electrostatic supported gyro monitor’s influence on spacecraft orbit determination precision

ZHOU Hai-yuan, WANG Xu-liang, LI Hong-yan, YANG Heng
(China Satellite Maritime Tracking & Controlling Department, Jiangyin 214431, China)

There was a big difference between TT&C-ship and ground control station in tracking a spacecraft orbit. The ground control station is static, and its orbit determination precision depends entirely on its radio equipment. While the TT&C-ship is dynamic, and its precision is determined more by the ship attitude precision than by its radio equipment. In order to improve the ship attitude’s measurement precision, an integrated INS/ESGM/GNSS navigation system is applied on TT&C-ship. According to the operation principle of the system and the data source selection during measurement of spacecraft orbit determination on TT&C-ship, a simulation is made to analyze the ship attitude data precision’s influence on the orbit determination precision. Simulations by the measured data of radar verify that the precision of spacecraft orbit determination is significantly improved by the data processing, showing that the TT&C-ship orbit determination precision can be improved by the ESGM.

electrostatic supported gyro monitor; integrated navigation system; date simulation; orbit determination precision

U666.1

A

1005-6734(2016)01-0006-03

10.13695/j.cnki.12-1222/o3.2016.01.002

2015-10-05；

2016-01-15

周海淵（1982—），男，工程師，從事慣性導航設備應用研究。E-mail: lynn9527@gmail.com