激光陀螺慣組系統級標定方法

孫偉強，張禮偉，熊 崴，陳 剛，曲 寧

（1.天津航海儀器研究所，天津 300131；2.海軍駐天津航海儀器研究所軍事代表室，天津 300131）

激光陀螺慣組系統級標定方法

孫偉強1，張禮偉2，熊 崴1，陳 剛1，曲 寧1

（1.天津航海儀器研究所，天津 300131；2.海軍駐天津航海儀器研究所軍事代表室，天津 300131）

針對激光陀螺慣性測量組件在傳統的分立式標定中受橡膠減震器影響的問題，從系統的角度對激光陀螺慣性測量組件的標度因數誤差、安裝誤差傳播規律進行分析。通過分別繞三只陀螺敏感軸轉動激發激光陀螺的標度因數誤差、安裝誤差，通過三只加速度計敏感軸分別指天激發加速度計的標度因數誤差、安裝誤差和零位，從而完成激光陀螺慣性測量組件的系統級標定。在未進行溫控及溫補的情況下，陀螺儀標度因數誤差重復性在3.5×10-6以內，安裝誤差重復性在3″以內，加速度計標度因數誤差和零位在其性能指標內，安裝誤差在4.5″以內。試驗結果表明，該方法滿足高精度、長期穩定性好的慣導系統工程應用要求。

捷聯慣性導航系統；機抖激光陀螺；慣性測量組件；系統級標定；卡爾曼濾波

慣性組件是慣性導航設備的核心設備，以激光陀螺為核心的激光陀螺慣性測量組件是目前最常用的高精度慣性測量設備。由于其直接固連于載體，感測載體角運動和線運動，如果慣性元件的安裝誤差、標度誤差較大，則會引起較大的系統誤差，因此對激光陀螺慣性測量組件進行精確標定必不可少。

傳統的標定方法是利用高精度三軸轉臺，進行速率試驗來標定陀螺儀的標度因數和安裝誤差，進行位置試驗來標定加速度計標度因數、安裝誤差和零位以及陀螺儀的零偏。由于機抖激光陀螺中引入了橡膠減震器，使慣性測量組件在翻轉過程中存在變形，用傳統的分立式標定方法，標定精度受到限制[1-3]。有多位學者從系統級角度出發，研究了系統級或在線對系統進行標定的方法[4-7]，但之前的研究很少有對系統級標定的轉位次序和參考坐標系建立的描述，而轉位次序對于系統的可觀測性具有重要意義[8-9]。本文從如何激發激光陀螺慣性測量組件誤差對系統導航參數影響的角度出發，分析轉位過程中標度誤差、安裝誤差傳播規律，設計合理的轉位順序和適用于激光陀螺慣性測量組件的卡爾曼濾波器，建立了以陀螺為參考系的系統級標定方法，研究雙軸位置轉臺條件下激光陀螺慣組系統級標定方法。

1 激光陀螺慣性測量組件誤差傳播規律分析

1.1 誤差模型

捷聯式系統誤差模型如下：

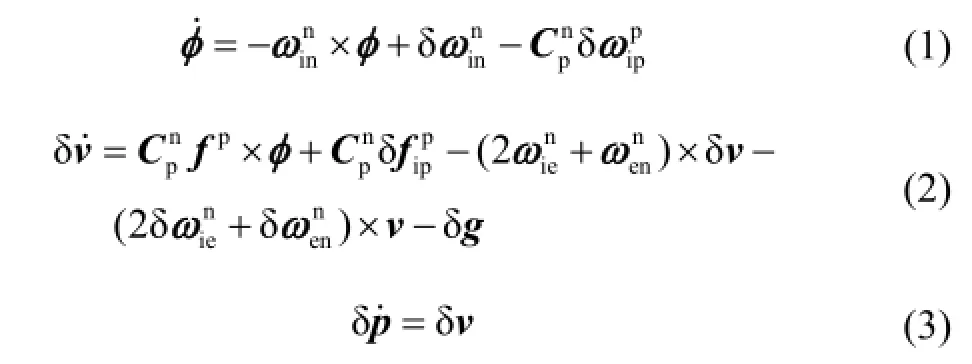
激光陀螺慣性測量組件誤差模型如下：

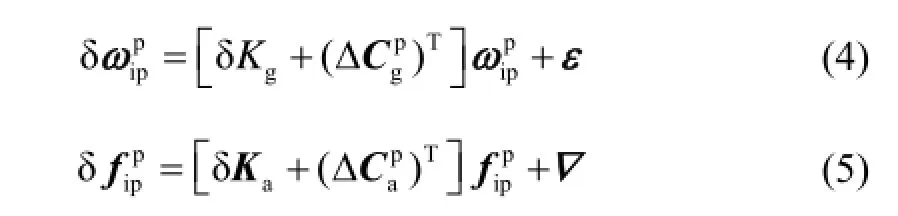
1.2 激光陀螺測量組件誤差激發過程分析

僅由陀螺誤差引起的姿態誤差方程如下：

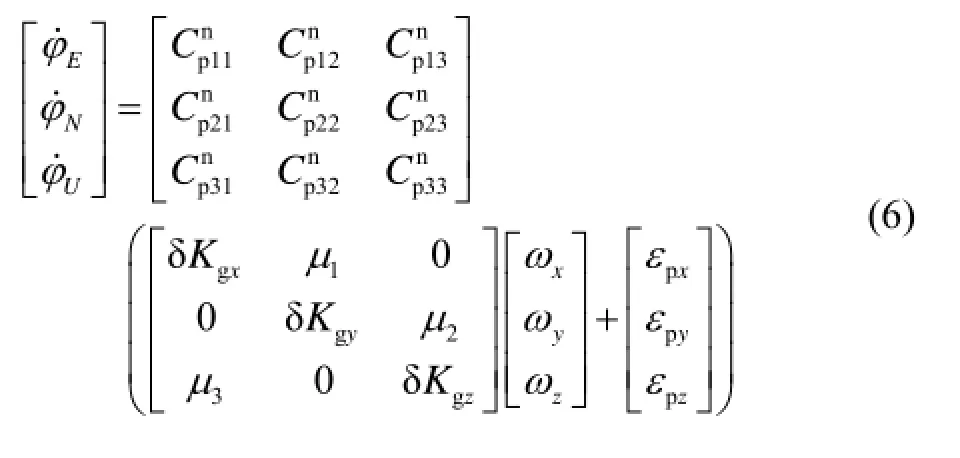
為分析方便，假設初始時刻載體坐標系與導航坐標系重合，即

若繞y陀螺敏感軸即橫搖軸進行旋轉，轉動角度為180°，則有：

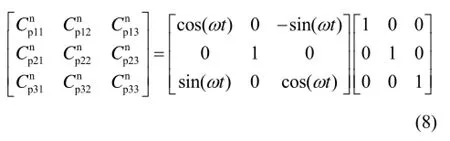
標定時采用的轉速ω約為15 (°)/s，地球自轉分量的量級earthω 約為10 (°)/h，由于相對于標定采用的轉速，地球自轉分量可以忽略不計，則有：

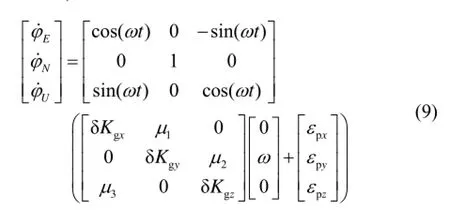
展開得：

對上面各式進行積分可得：

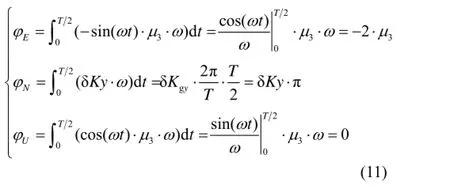
即繞y陀螺敏感軸轉動180°，陀螺安裝誤差、標度因數誤差引起的姿態誤差為

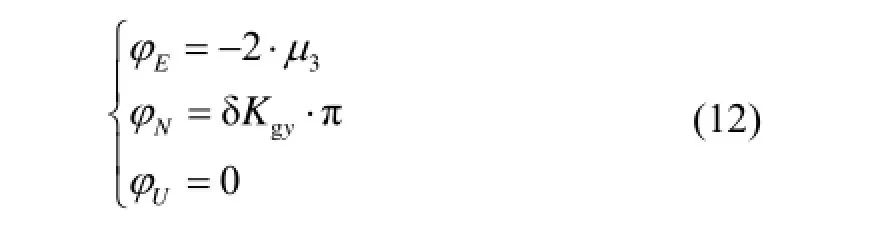
繞z陀螺敏感軸即繞方位軸轉過180°，同樣得忽略地球自轉的影響，有：

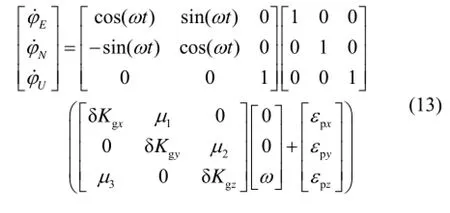
展開得：

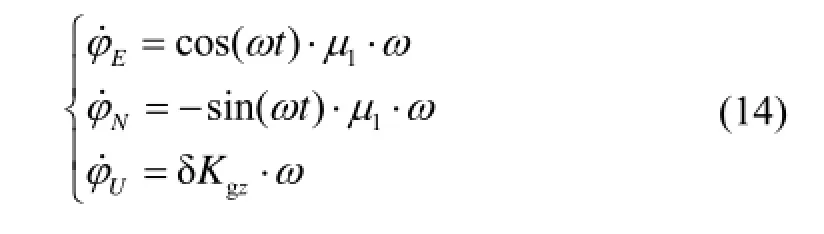
對上面各式進行積分可得：

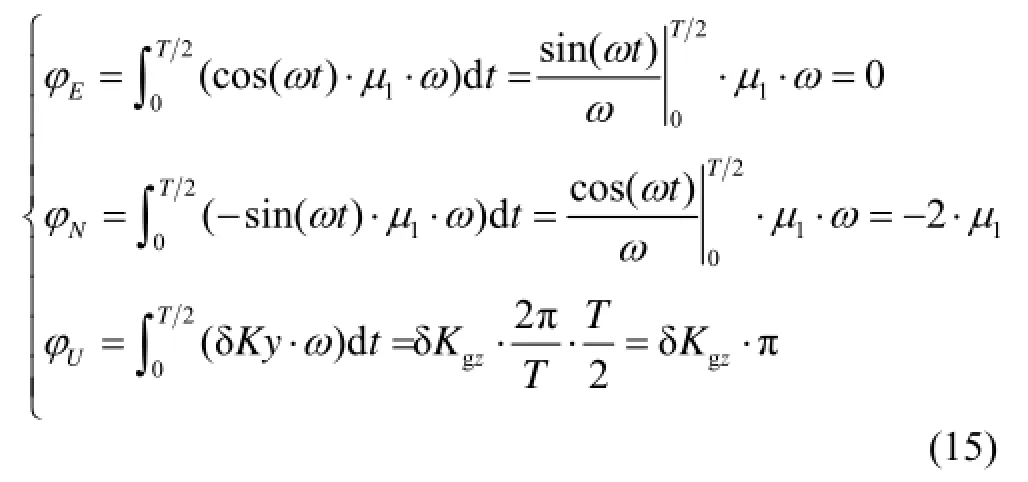
即繞z陀螺敏感軸轉動180°，陀螺安裝誤差、標度因數誤差引起的姿態誤差為

繞方位軸轉動90°，則x陀螺敏感軸指向橫搖軸，此時繞x陀螺敏感軸轉動，則有：

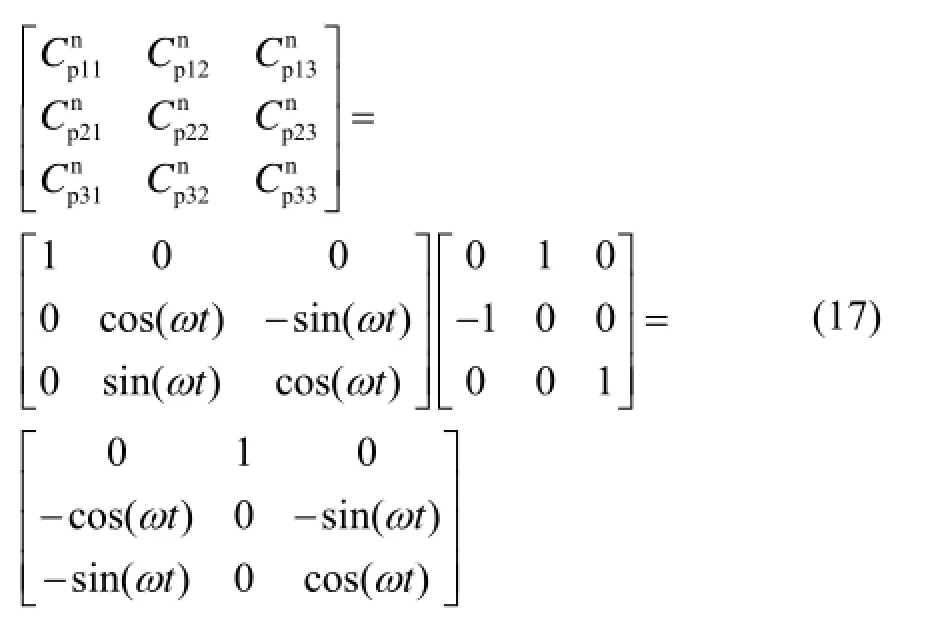
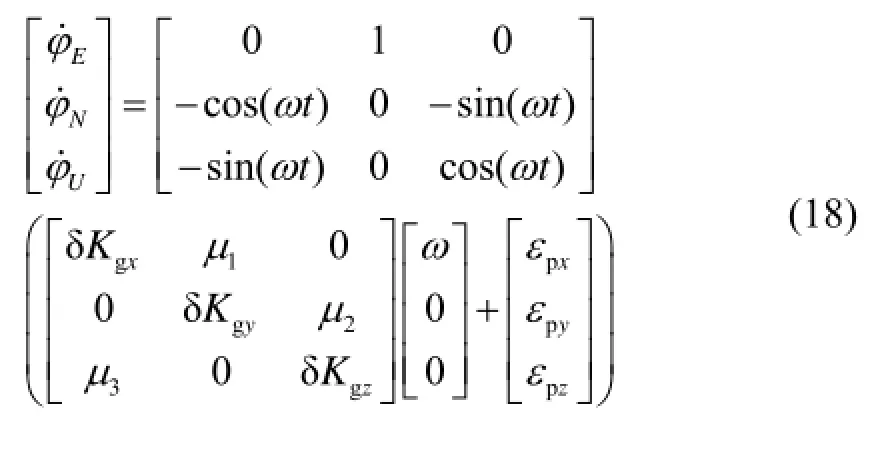
展開得：

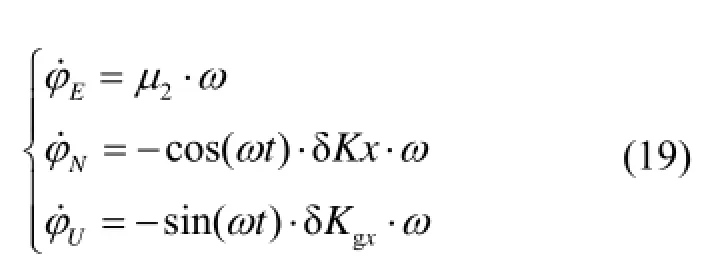
對式(19)各項進行積分，得：

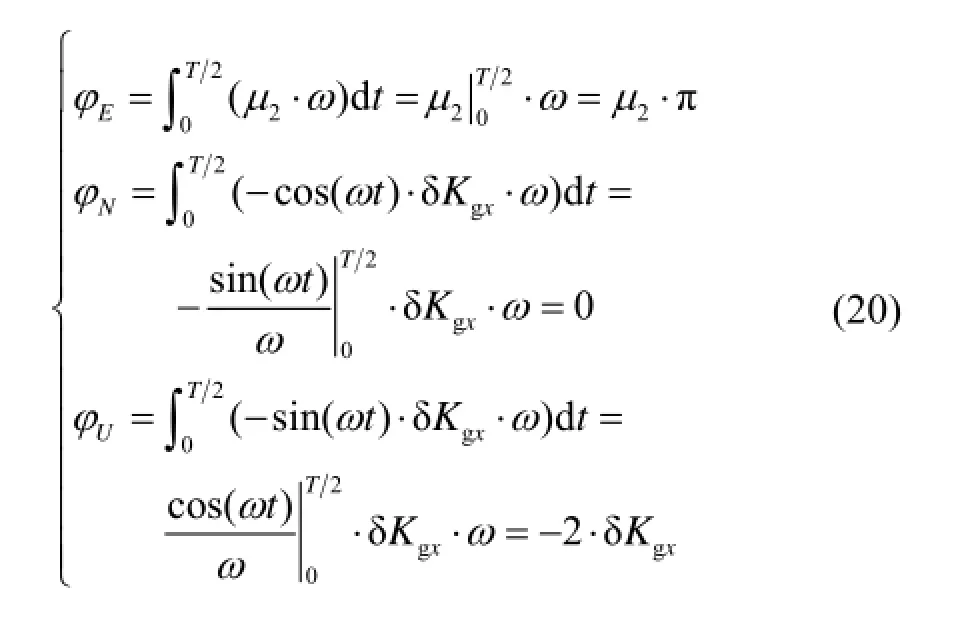
即繞x陀螺敏感軸轉動180°，陀螺安裝誤差、標度因數誤差引起的姿態誤差為

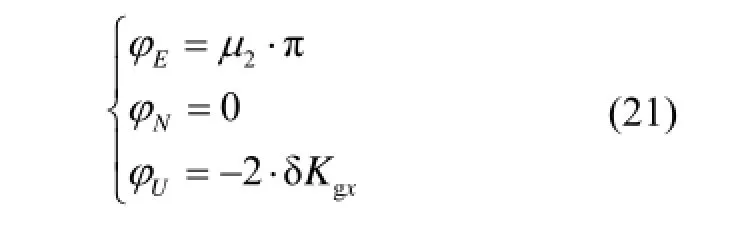
從式(12)(16)(21)可以看出，通過分別繞三個陀螺儀敏感軸旋轉均可以激發出標度因數誤差和三個安裝誤差，且相互之間沒有耦合，據此可以設計出適用于系統級標定的轉位次序。陀螺儀常值誤差可以通過使各個陀螺敏感軸分別指向北向，利用卡爾曼濾波器將其估計出來。

1.3 加速度計測量組件誤差激發過程分析

對于加速度計，有：

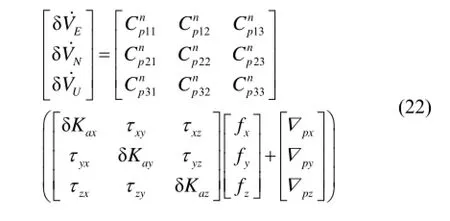
為分析方便，假設初始時刻載體坐標系與導航坐標系重合，此時 z加速度計敏感軸指天，則有

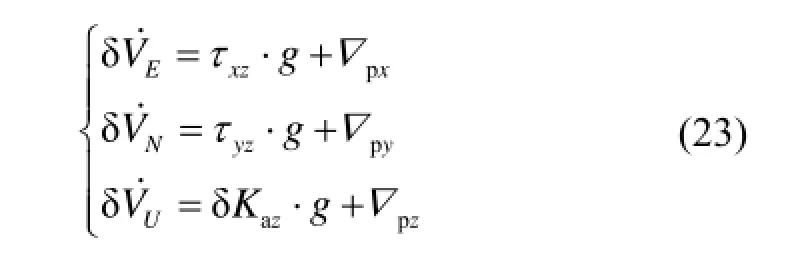
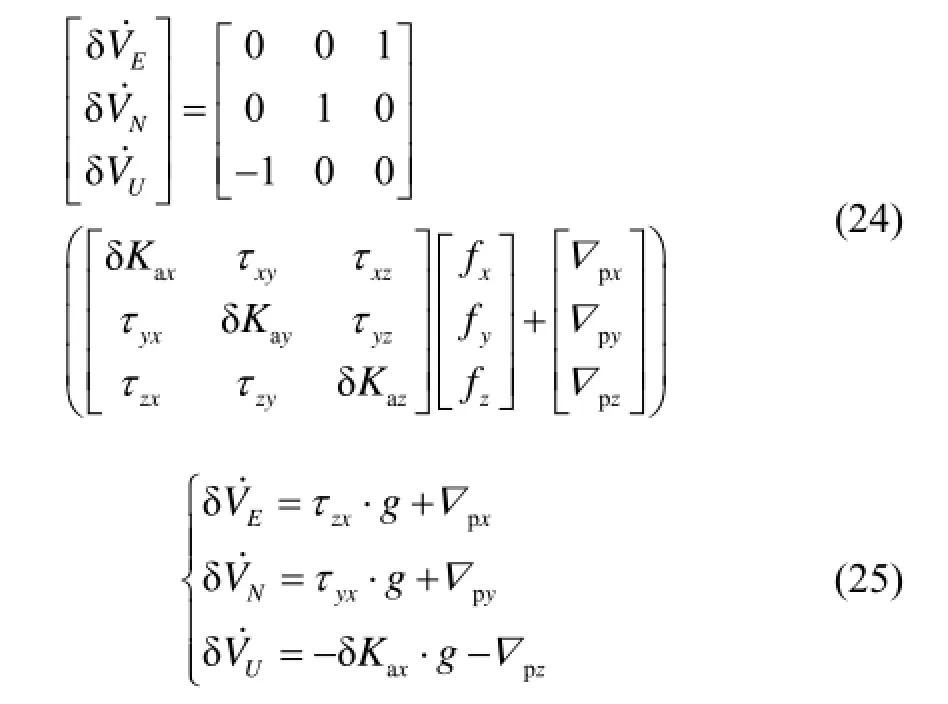
繞方位軸轉過90°，再繞橫搖軸轉過90°，此時y加速度計敏感軸指天，則有：

式(23)(25)和(27)表明了加速度計各項誤差的激發情況，由于加速度計零位是不隨敏感加速度量的變化而變化的，因此可以據此在各式的基礎上旋轉180°，來估計加速度計零位，由此可以將加速度計的各項誤差均估計出來。

2 系統級標定方案設計

以式(1)～式(5)為系統誤差模型建立 27維卡爾曼濾波器，對慣性測量組件各項誤差進行標定，系統狀態矢量如式(28)，卡爾曼濾波器方程如式(29)～(33)[10]。

式(28)中各量的具體含義參見第2節。

狀態一步預測：

一步預測誤差方差陣：

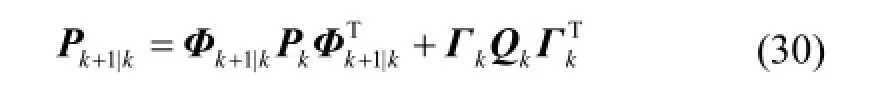
濾波增益矩陣：

估計誤差方差陣：

狀態估計：

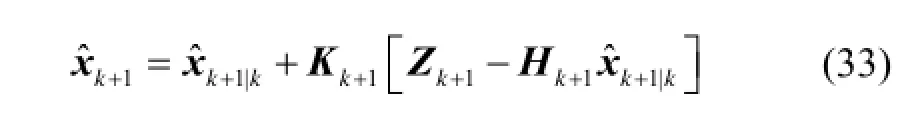
表1給出了系統級標定過程中轉臺的轉動次序及每次轉動的角增量。

表1 陀螺儀系統級標定次序Tab.1 Sequence of gyro systematic calibration

3 標定試驗

利用三只高精度陀螺儀構成的慣性測量組件和轉臺，進行了系統級標定試驗。標定過程中，陀螺儀和加速度計的標度因數采用粗略計算出來的值，陀螺儀和加速度計的安裝誤差設為 0，陀螺儀和加速度計的常值漂移誤差設為 0，按照設定的轉位次序進行旋轉激發各項誤差，采集陀螺儀和加速度計數據進行卡爾曼濾波，對各項誤差進行估計。由于陀螺儀零偏誤差需要做長時間測漂估計，受時間限制本次試驗未做，加速度計標度因數受溫度影響較大，而本次試驗未做溫度控制和溫度補償。在未進行溫控及溫補的情況下，陀螺儀標度因數誤差重復性在3.5×10-6以內，安裝誤差重復性在3″以內，加速度計標度因數誤差和零位在其性能指標內，安裝誤差在4.5″以內。圖1～圖3給出了某次試驗各項誤差收斂曲線。

圖1 陀螺儀標定結果Fig.1 Calibration results of gyro

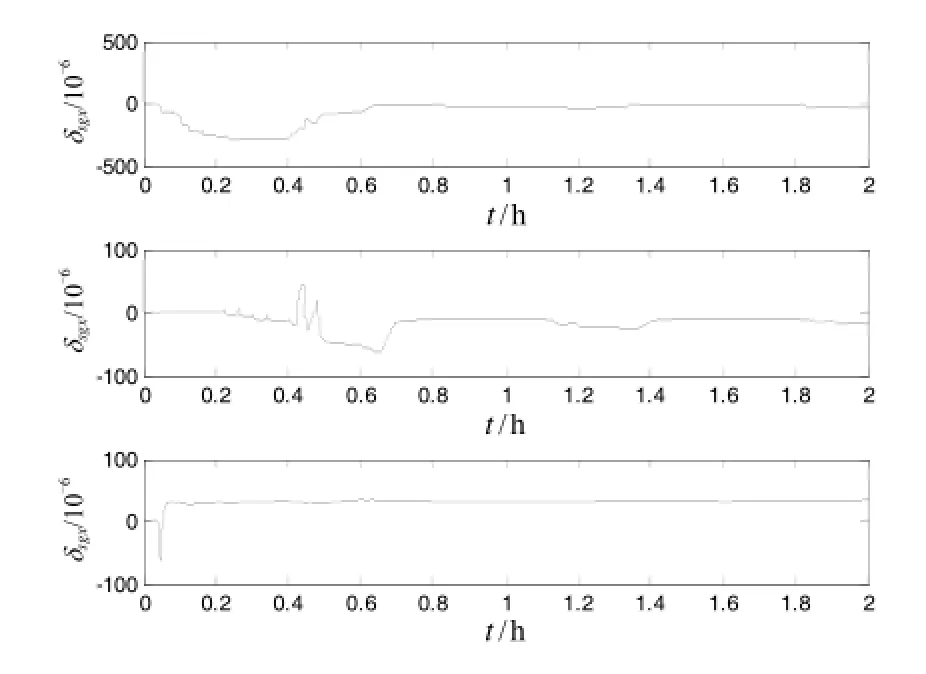
圖2 加速度計標度因數標定結果Fig.2 Calibration results of acc scale

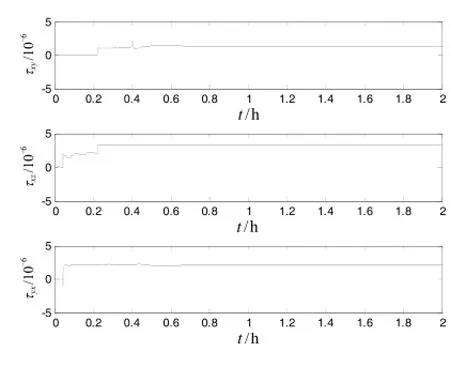
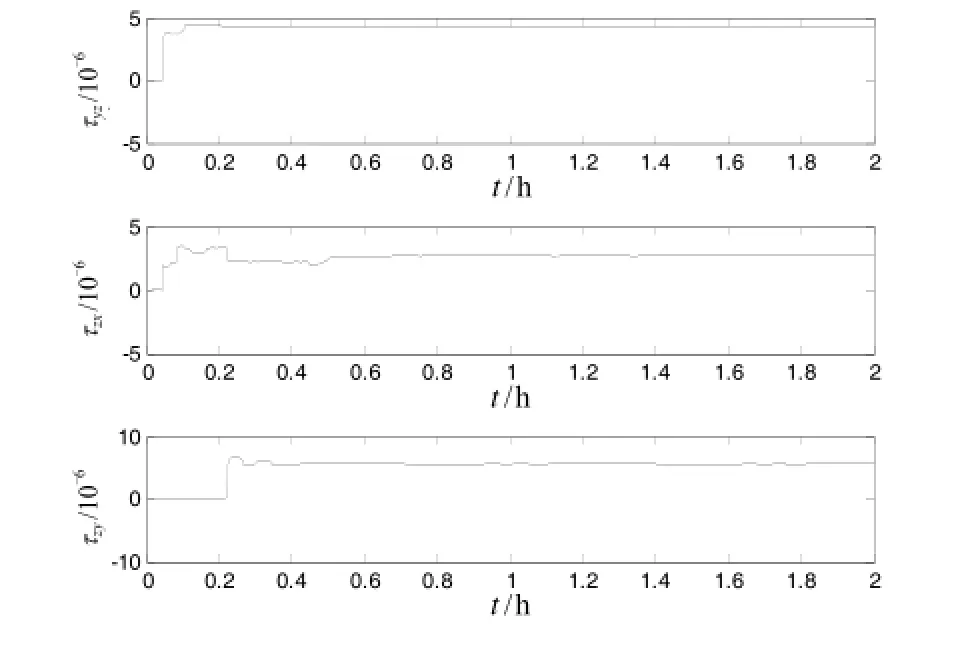
圖3 加速度計安裝誤差標定結果Fig.3 Calibration results of acc misalignment

4 結 論

本文從系統的角度對激光陀螺慣性測量組件的標度因數誤差、安裝誤差的傳播規律進行分析，通過分別繞三只陀螺敏感軸轉動激發激光陀螺的標度因數誤差、安裝誤差，通過三只加速度計敏感軸分別指天激發加速度計的標度因數誤差、安裝誤差和零位，從而完成激光陀螺慣性測量組件的系統級標定。試驗結果表明，該方法具有一定的工程應用價值。

（References）：

[1] 吳文啟, 張巖, 張曉強, 等. 激光陀螺接連慣導系統參數穩定性與外場自標定[J]. 中國慣性技術學報, 2011, 19(1): 11-15.

Wu Wen-qi, Zhang Yan, Zhang Xiao-qiang, et al. Parameter stability and outfield self-calibration of RLG-SINS [J]. Journal of Chinese Inertial Technology, 2011, 19(1): 11-15.

[2] 楊曉霞, 孟浩然, 王帥. 激光捷聯慣導系統的外場動態標定方法[J]. 中國慣性技術學報, 2011, 19(4): 393-398.

Yang Xiao-xia, Meng Hao-ran, Wang Shuai. Calibration method for laser gyro SINS under outer field dynamic conditions[J]. Journal of Chinese Inertial Technology, 2011, 19(4): 393-398.

[3] 魏國. 二頻機抖激光陀螺雙軸旋轉慣性導航系統若干關鍵技術研究[D]. 國防科技大學碩士學位論文, 2013.

Wei Guo. Research on some key technologies for dualaxis rotation inertial navigation system with mechanically dithered ring laser gyroscope[D]. Ph.D Thesis of National University of Defense Technology, Changsha, China, 2013.

[4] 陸志東, 王曉斌. 系統級雙軸旋轉調制捷聯慣導誤差

分析及標定[J]. 中國慣性技術學報, 2010, 18(2): 135-141. Lu Zhi-dong, Wang Xiao-bin. Error analysis and calibration of systematic dual-axis rotation modulating SINS[J]. Journal of Chinese Inertial Technology, 2010, 18(2): 135-141.

[5] Xiong Zhi, Peng Hui, Liu Jian-ye, et al. Online calibration research on the lever arm effect for the hypersonic vehicle[C]//Proceedings of the 2014 IEEE/ION Position, Location and Navigation Symposium: 1213-1218.

[6] J?rgensen M J, Paccagnan D, Poulsen N K. IMU calibration and validation in a factory, remote on land and at sea[C]//Proceedings of the 2014 IEEE/ION Position, Location and Navigation Symposium: 1384-1391.

[7] 黃鳳榮, 侯斌, 孫偉強, 等. 雙軸旋轉式 SINS自主標定技術[J]. 中國慣性技術學報, 2012, 20(2): 146-151.

Huang Feng-rong, Hou Bin, Sun Wei-qiang, et al. Selfcalibration for dual-axis rotary SINS[J]. Journal of Chinese Inertial Technology, 2012, 20(2): 146-151.

[8] Chang Guo-bin, Xu Jian-ning, Li An, et al. Error analysis and simulation of the dual-axis rotation-dwell auto compensating strap-down navigation system[C]//2010 International Conference on Measuring Technology and Techtronic Automation. 2010: 124-127.

[9] Goshen-Meskin D, Bar-Itzack L Y. Observability analysis of piece-wise constant systems with application to inertial navigation[C]//Proceedings of the 28th Conference on Decision and Control. Honolulu, Hawail, 1990.

[10] Shin Eun-Hwan. Estimation techniques for low-cost inertial navigation[R]. The University of Calgary, 2005.

Systematic calibration method for RLG inertial measurement unit

SUN Wei-qiang1, ZHANG Li-wei2, XIONG Wei1, CHEN Gang1, QU Ning1
(1. Tianjin Navigation Instrument Research Institute, Tianjin 300131, China; 2. Navy Army Military Representative Department in Tianjin Navigation Instrument Research Institute, Tianjin 300074, China)

To avoid the distortion of the elastic isolation of the IMU in traditional calibration method, the transmission rule of the scale factor and installation error in SINS was analyzed. Each of the gyro’s three sensitive axes was rotated to separately excite the scale error and fix error, and the accelerometer axis was pointed up and down to separately excite the scale error, misalignment and bias to realize the systematic calibration of laser gyro inertial measurement units. The experiment results show that, when without temperature compensation and control, the gyro’s scale factor error repeatability is within 3.5×10-6, the gyro’s misalignment repeatability is within 3″, the accelerometer’s misalignment is within 4.5″, and the accelerometer’s scale factor and biases are all within the performance specifications, which show that the proposed calibration method meets the engineering requirements of long-time and high-accuracy inertial navigation system.

SINS; dithered ring laser gyro; inertial measurement unit; systematic calibration; Kalman filter

U666.1

A

1005-6734(2016)01-0009-05

10.13695/j.cnki.12-1222/o3.2016.01.003

2015-09-05；

2015-11-29

船舶預研支撐技術基金（14J3.9.4）

孫偉強（1984—），男，工學碩士，高工，主要從事捷聯式慣性導航系統研究。E-mail: sunwq1984@163.com