高阻尼橡膠支座的本構模型研究綜述*

張菊輝，陳 楊

(上海理工大學 環境與建筑學院，上海 200093)

為了減少地震作用對橋梁結構的破壞，許多減、隔震技術興起，如結構基礎隔震技術、疊層橡膠隔震技術等。其中，比較前沿的減隔震裝置是高阻尼橡膠支座，它是由普通橡膠用硫化技術將橡膠層和鋼墊片結合成一體，并添加炭黑、增塑劑、油等材料。這種支座能顯著增加結構阻尼和延長結構周期[1]，不僅具有良好的隔震性能，而且能避免發生生態污染[2]，已經逐漸成為鉛芯橡膠支座的替代產品。

近20年來，研究者針對高阻尼橡膠支座性能進行了大量實驗研究，力學性能如單軸受壓受剪[3]、水平雙軸受力[4]、多軸受力[5]、等效阻尼比和等效水平剛度[6]等；影響力學性能的因素如速度相關性、加載歷程等[7-8]；物理性能如黏性[9-10]、蠕變[11]等，但在探討適合高阻尼橡膠支座力學性能的本構模型方面研究較少。在有限元分析中，大多直接采用程序自帶的溫氏模型來模擬高阻尼橡膠支座的本構關系，但該模型對高阻尼橡膠的特征性研究較少。高阻尼橡膠材料的超彈性力學模型是建立在普通橡膠材料基礎上的[12]129，因此，本文從普通橡膠材料出發，對比分析了多種用來描述普通橡膠材料在靜載作用下的超彈性本構模型，結合高阻尼橡膠本構理論的推導，綜述了目前國內外提出的幾種能較好模擬高阻尼橡膠支座力學性能的本構模型，為高阻尼橡膠支座的進一步研究提供理論依據和參考。

1 高阻尼橡膠本構理論的引出

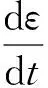
盡管已知算法，但將各個元件的應力、應變進行簡單疊加從而得出本構方程的這種做法是不可取的。雖然進行“疊加”的思路并沒有錯，但是忽略了下面3個關鍵問題：(1)橡膠材料屬于一種黏彈性材料，既有固體的彈性又有液體的黏性，而這種黏性會導致應力松弛和蠕變現象，這2種現象與時間和溫度2個因素有關；(2)高阻尼橡膠支座在水平剪切實驗中的變形涉及大變形彈塑性固體理論，在連續介質力學中，這種大變形會涉及到構架變化，并不能保證未變形前的應力張量在構架變化后其方向和大小不變，故也證明了簡單疊加的錯誤性；(3)簡單疊加不能描述橡膠材料的高度非線性[14]，即在靜載作用下的非線性彈性行為，在循環荷載作用下的黏彈性行為，在預應力作用后表現的應力軟化現象，即Mullins效應。

因此，本構模型的建立要從基本假設入手。建立的本構方程能否真實地反映材料的響應特性，必須滿足如下2個基本原則：(1)構架無差異性原理或者客觀性要求，即需要尋找材料中的某種場量，該場量能簡單地隨構架的旋轉而旋轉；(2)熱力學相容性要求，即滿足能量守恒定律以及熵增原理。

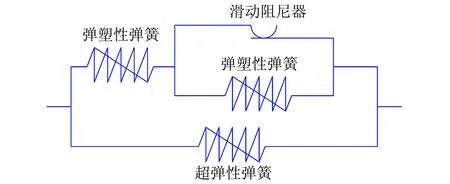
圖1 Yoshida等提出的高阻尼橡膠材料本構模型

1.1 基本假設

對高阻尼橡膠支座的實驗研究多在準靜態加載條件下進行，Yoshida等[12]131做如下假設：(1)彈性體變形過程絕熱；(2)荷載加得足夠慢，彈性體隨時處于平衡狀態，而且動能可忽略不計，并且在變形過程中，內能沒有變化，彈性體的熵是所有長鏈分子熵的總和，可以根據熱力學公式推導出其滿足熱力學定律；另外高阻尼橡膠假設為各項同性且均勻和可壓縮性材料[15]。其應變能函數W可表示成偏應變能WD和靜水壓力應變能WH之和，如式(1)所示。

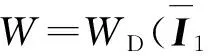
(1)

式(1)右邊2項都包含體積變化的影響，其中右邊第一項由構型熵的變化引起，第二項由熱力學能引起。但式(1)不能定性說明靜水壓力實驗和單軸拉伸實驗數據[16]，即使小變形情況也不能做到定性解釋。

1.2 彈塑性部分

Yoshida等根據Graesser和Gozzarelli[17]所提出的耗能材料，如鋼、銅在無限小變形的本構模型基礎上，將其引申到有限變形的問題上，并提出了可以用來描述高阻尼橡膠支座本構模型中彈塑性部分特征的數學表達式，如式(2)所示。

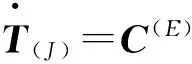
(2)

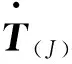
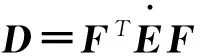
(3)

(4)

(5)

將式(3)和式(4)代入式(5)可以導出式(6)。

(6)

(7)

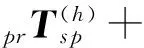
(8)

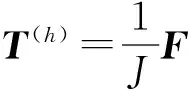
(9)

(10)

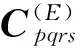
(11)

(12)

(13)

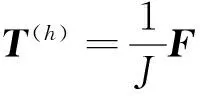
(14)

(15)

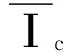
1.3 超彈性部分

超彈性材料的特征是存在一個潛在(或應變)的能量函數，它是應力S的勢能，如式(16)所示。

(16)

式中：φ為潛在勢能函數，當以格林應變E為變量的函數用以表示潛在勢能函數時，可以將該函數記為應變能密度函數U；c為材料參數，這里兩個標量函數的關系如式(17)所示。

U(E)=φ(2E+I)

(17)

式中：I為與E階數相同的單位矩陣。

由于在橡膠類材料中可以觀察到橡膠材料的大變形這一特征。大變形前后的時間間距較短，變形過程中間發生的情況也比較復雜，如應力應變非線性、與時間相關的應力應變響應、Mullins效應等。為了描述功獨立于變形路徑，需要引用潛在勢能函數，其結果是超彈性材料上做功并獨立于變形路徑。考慮變形狀態下每單位參考體積潛在能量從c1至c2的變化，采用Piola-Kirchhoff應力張量S與格林應變E的功共軛形式如式(18)所示。

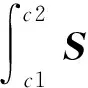
(18)

可見，儲存在材料中的能量僅取決于變形的初始狀態和最終狀態，并且獨立于變形或荷載路徑，故也滿足基本假設中的構架無差異性。

2 高阻尼橡膠支座超彈性本構模型的選擇

2.1 橡膠材料超彈性本構模型的分類

橡膠材料的超彈性本構模型可以分為2大類[18-19]：(1)熱力學統計的本構模型。橡膠分子網鏈的研究是基于非高斯統計模型，這種網鏈由很多任意方向上長的柔性分子鏈組成，分子與分子之間通過稀疏的交聯點組成分子網絡，這也導致了分子之間的連接很弱，所以橡膠的應力應變行為由構象熵決定[18]51。另一方面，這種分子網鏈結構使橡膠材料能夠產生大應變的超彈性變形，構象數會隨著分子鏈段內的內旋運動而改變。當沒有外力作用時，分子鏈總是趨向于熵最大的卷曲構象，當有外力作用時，構象的改變會引起構象熵的改變[20]；(2)唯象學的本構模型。唯象學的描述方法假設在未變形橡膠為各項同性材料，即在橡膠中長鏈分子的方向是隨機分布的，這種各項同性的假設是用單位體積(彈性)應變能密度來描述橡膠特性的，具體分類如表1所示。

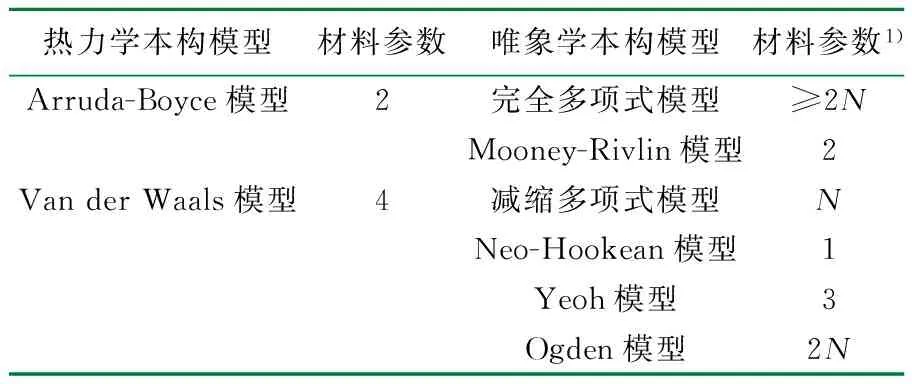
表1 有限元分析中的2類橡膠本構模型

1)N為多項式的次數。

2.1.1 多項式形式本構模型

對于各項同性材料，將應變能密度分解為2部分，如式(19)所示。

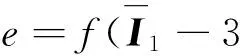
(19)

(20)

式中：參數N為多項式階數，材料是否可壓縮取決于Di的值，如材料是完全不可壓縮的，那么所有的Di都為0。

2.1.2 Mooney-Rivlin形式和Neo-Hookean形式的本構模型

在多項式本構模型中，如果設定材料參數Cij=0(j≠0)，則得到減縮多項式模型如式(21)所示。

(21)

如果只要保留線性部分的應變能量，可以令完全多項式本構模型中的階數N=1，即Mooney-Rivlin形式的本構模型為式(22)。

(22)

對于減縮多項式，如果令階數N=1，則得到Neo-Hookean形式的本構模型如式(23)所示。

(23)

這種模型的優點在于無條件穩定性，即如果已知一種變形方式下應力-應變曲線擬合的材料常數，那么就能用來在小應變到中等應變的范圍內預測其它變形方式的應力-應變曲線[18]54，因此在不知道材料的精確參數情況下，可以選擇這種模型。

上述2種本構模型都是采用不變量的線性函數，所以它們的精度相近。由于階數N的取值比較低(N=1),導致這2種函數在應力-應變曲線中大應變階段時不會出現拐點，即不會出現陡升行為，但在小應變(<1%)和中等應變(1%～10%)時可以很好地模擬材料特性[13]173，如圖2所示。

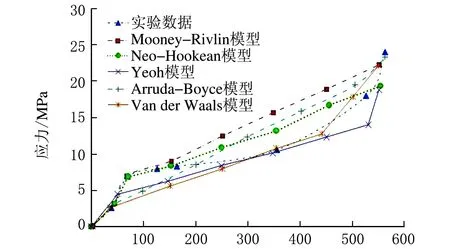
應變/%圖2 各種橡膠材料超彈性本構模型與實驗數據對比

2.1.3 Yeoh形式本構模型

在減縮多項式的基礎上令階數N=3，可以得到Yeoh形式的本構模型,如式(24)所示。

(24)

材料參數C10之間的變化規律[13]173為：如果C10=0(1)，第2個系數將為負數，比第1個系數小1～2個數量級，即小于10-1～10-2，第3個系數再小1～2個數量級并且為正。這種一正一負的數量級關系將產生典型的S型橡膠應力-應變曲線。

2.1.4 Ogden形式本構模型

基于橡膠彈性的分子網絡模型，可以通過分子鏈的伸長來表示，這樣得到了Ogden形式的本構模型。該模型的應變能密度函數以3個主伸長率λ1,λ2,λ3為變量[23-25]，具體表示如式(25)所示。

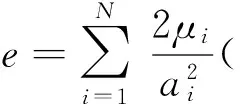
(25)

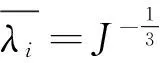
該模型的優點在于使用伸長率表示應變能密度函數，與用應變不變量表示的Rivlin模型僅有外觀上的不同。在有限元分析中，應變能函數無論用應變不變量還是用主伸長率來表示，只要擬合系數足夠精確合理，其計算結果都不受影響[26]53。

2.1.5 Arruda-Boyce形式本構模型

Arruda-Boyce模型也稱為八鏈模型，可以通過熱力學統計方法得到5個材料參數C值，與唯象學中的模型不同，熱力學的材料參數C都具有物理意義。Arruda-Boyce形式本構模型應變能密度函數如式(26)所示。

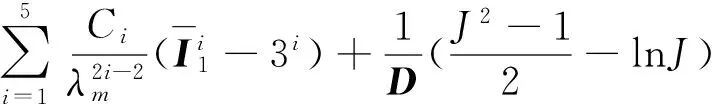
(26)

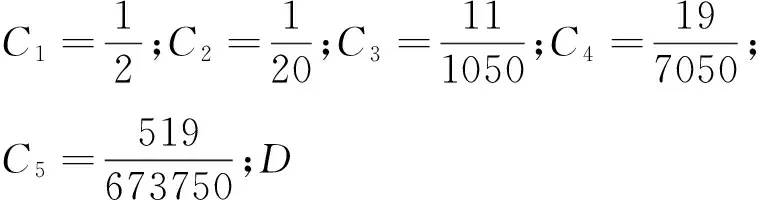
初始體積模量K0=2/D，因為函數中只有2個參數，即使已知很少的材料行為，也可以得到本構關系。Kaliske和Rothert證明了這種體積應變能密度表達式可以應用于大部分工程彈性材料，并保證結果足夠精確。這2個參數即使數值發生改變，也不會改變曲線形狀。如果實驗數據得出的曲線形狀和該模型預測曲線形狀不同，那么這種本構模型就不能很好地模擬材料特性。

2.1.6 Van der Waals形式的本構模型

Van der Waals模型定義的應變能密度函數如式(27)所示。

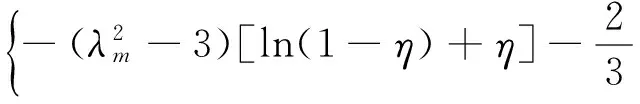
(27)

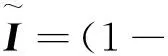
在很多情況下，與Neo-Hookean形式相比，由于Mooney-Rivlin模型中的多項式數量更多，Mooney-Rivlin模型會得到與實驗數據更接近的解,如圖2所示，但是它們的應變能密度函數都是由不變量組成線性函數，所以它們的精度相近。這2種函數階數的取值較低，故在應力-應變曲線的大變形部分不會出現拐點，不能表示硬化現象，但是在小應變和中等應變時可以很好地模擬材料特性。Yeoh模型由于特殊量級關系可以產生典型的S型橡膠應力-應變曲線，這也與實驗數據曲線形狀較為接近。如果橡膠本構模型的基礎實驗數據齊全，如單軸拉伸、等軸拉伸和平面拉伸數據，盡量采用高階的Ogden模型或是多項式模型。Arruda-Boyce模型的材料參數只有2個，曲線的形狀與這2個材料參數無關，如果實驗數據和Arruda-Boyce模型預測的曲線形狀不同，這種本構模型就不能很好地模擬材料的特性，而Van der Waals模型相比Arruda-Boyce模型的優點在于可以更好地擬合實驗數據，不但可以改變應力-應變的比例，而且可以改變曲線的形狀。

2.2 適合于高阻尼橡膠支座的超彈性本構模型

高阻尼橡膠除具有和普通橡膠一樣的基礎力學性能外，還具有較高的滯回耗能性能[12]129。因此，高阻尼橡膠的超彈性本構模型，應以普通橡膠材料的超彈性本構模型為基礎，并考慮高阻尼橡膠在大變形下的強化和應變歷史相關性。這里推薦使用的Yoshida等本構模型，如圖1所示。該模型在應變能函數式(1)的基礎上，引入彈塑性彈簧模擬大變形下的強化和應變歷史相關性。具體本構方程如式(28)所示。

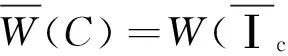
(28)

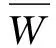
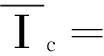
(29)

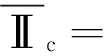
(30)

最新的研究表明，高阻尼橡膠支座具有速度相關性，會對滯回環面積、屈服后剛度等因素產生較大影響，并對加載速度敏感，因此在其力學模型中必須考慮速度相關性，Bhuiyan等[10]1778使用了流變模型來模擬高阻尼支座的速度相關性。Tsai等[27]在溫氏模型的基礎上推導出考慮速度相關性的數值模型并應用于有限元分析，上述2種模型都是基于實驗得到的支座滯回曲線進行模擬。近年來，對Yeoh模型的研究發現其不能很好地模擬高阻尼橡膠復雜的力學性能，特別是高阻尼橡膠材料初始剛度很大的特性[28]。因此袁涌等[29]74在Yeoh的基礎上提出了一個基于改進超彈性Zener模型的高阻尼橡膠隔震支座速度相關性本構模型，模型示意圖如圖3所示。

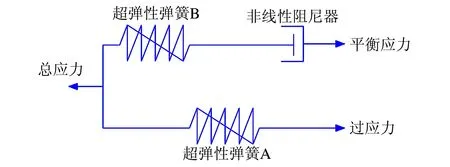
圖3 改進的超彈性Zener模型

當荷載的施加速度無限慢時，非線性阻尼器將力阻隔，力只從超彈性彈簧A一邊通過，故而其平衡應力相當于總應力，這時稱模型處于平衡狀態。反之，當荷載的施加速度無限快時，非線性阻尼器被視做剛體，總應力等于超彈性彈簧A和B的應力總和，這時稱模型處于瞬時反應狀態。當處于這2種極限狀態之間時，高阻尼橡膠支座的速度相關性可以用非線性阻尼器自帶的黏滯性來模擬[29]76。其超彈性的本構方程是在Yeoh基礎上提出的一個新的應變能函數，該函數表示為第一應變不變量的多項式，另外使用附加剛度系數α來模擬高阻尼橡膠較大的初始剛度[26]60，具體表達式如式(31)和式(32)所示，Kroner分解示意圖[30]如圖4所示。

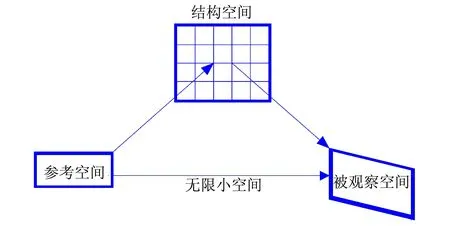
圖4 Kroner分解示意圖

彈簧A：

(31)

彈簧B：

(32)

式中：CiA(i=1～4)；CjB(j=1～5)；α為橡膠材料參數；WA、WB為彈簧A和彈簧B的應變能密度函數；I1A、I1B分別為彈簧A和彈簧B的應變張量不變量。

3 結束語

高阻尼橡膠的本構理論主要從連續介質力學和黏彈性力學推導而來，而本構模型主要從統計熱力學和唯象法兩個方面進行研究。唯象法的優點在于通過選取合理的應變能密度函數階數和材料參數將函數曲線近似趨近于實驗數據曲線，針對各種實驗工況結果，能夠描述材料較大的變形范圍。唯象法的缺點是其參數沒有物理意義，缺乏對材料本質的認識[18]56。近年來，在統計熱力學中以非高斯統計模型為基礎的本構模型日益發展，從一定程度上解釋了大變形時分子的非高斯特性，由此也找到了以應變不變量表示的唯象學模型和分子統計熱力學本構模型之間的一些關系。

由于橡膠材料的特性十分復雜，因此在建立這些理論模型時不得不做一些假設，導致各種模型會出現不足之處。比如假設橡膠變形時是連續的，但高阻尼橡膠支座在大變形前后，其內部中間部分的體積變形至今還未有相關研究，并且在連續介質力學中將內部中間部分看成無限小空間，如圖4所示。也就是說忽略了大變形前后材料內部的分子變化。故若將該部分進行完善，那么高阻尼橡膠支座的本構模型也會進一步發展。在實際應用中，往往有多種因素導致高阻尼橡膠支座在其工作壽命范圍內提前失效，其主要原因是：(1)選擇的橡膠阻尼性能不理想。影響阻尼性能的因素如損耗因子、玻璃化轉變溫度以及阻尼峰半高寬溫度范圍。解決方法是將橡膠的工作溫度區域拓寬等，利用的現有技術包括橡膠與高聚物共混、互穿網絡聚合物、硫化體系等；(2)高阻尼橡膠支座的選擇缺乏相應的理論依據，在選擇合適的支座時，應當考慮如橋梁場地工況、伸縮縫長度以及主梁和擋石之間的距離能否滿足其變形要求等。現階段對第二個主要原因的研究相對較少，若能夠提出明確的選取標準，則能大大增加高阻尼支座的壽命以及使用率。

參 考 文 獻：

[1] 黨育，杜永峰，李慧.基礎隔震結構設計及施工指南[M].北京:中國水利水電出版社，2007.

[2] 袁涌，朱昆，熊世樹，等.高阻尼橡膠隔震支座的力學性能及隔震效果研究[J].工程抗震與加固改造，2008，30(3):15-20.

[3] AMIN A F M S，WIRAGUNA S I，BHUIYAN A R，et al.Hyperelasticity model for finite element analysis of natural and high damping rubbers in compression and shear[J].Journal of Engineering Mechanics，2006，132(1):1-11．

[4] YAMAMOTO MASASHI，MINEWAKI SHIGEO，YONEDA HARUMI，et al.Nonlinear behavior of high-damping rubber bearings under horizontal bidirectional loading:full-scale tests and analytical modeling[J].Earthquake Engineer and Structural Dynamics，2012，41:1845-1860.

[5] ABE MASATO，ASCE M，YOSHIDA JUNJI，et al.Multiaxial behaviors of laminated rubber bearings and their modeling:I:experimental study[J].Journal of Structural Engineering，2004，130(8):1119-1132.

[6] 中交第一公路勘察設計院有限公司.公路橋梁高阻尼隔震橡膠支座：JT/T842—2012[S].北京:人民交通出版社，2012.

[7] 袁涌，朱宏平，資道銘，等.高阻尼橡膠隔震支座的力學性能及隔震效果分析研究[J].預應力技術，2008，1(84):20-33．

[8] 沈朝勇，周福霖，崔杰，等.高阻尼隔震橡膠支座的相關性試驗研究及其參數取值分析[J].地震工程與工程振動，2012，32(6)：95-103.

[9] AMIN A F M S，LION A，SEKITA S，et al.Nonlinear dependence of viscosity in modeling the rate-dependent response of natural and high damping rubbers in compression and shear:Experimental identification and numerical verification[J].International Journal of Plasticity，2006，22(9):1610-1657.

[10] BHUIYAN A R，OKUI Y，MITARUMA H，et al.A rheology model of high damping rubber bearings for seismic analysis:identification of nonlinear viscosity[J].International Journal of Solids and Structures，2009，46(7/8):1778-1792.

[11] KATO HIDEAKI，MORI TAKAHIRO，MUROTA NOBUO，et al.An analytical model for elastoplastic and creep-like behavior of high-damping rubber bearings[J].Struct Eng，2015，141(9):1-9.

[12] YOSHIDA JUNJI，ABE MASATO，ASCE M，et al.Constitutive model of high-damping rubber materials[J].Journal of Engineering Mechanics，2004，130(2):129-141.

[13] 張少實，莊茁.復合材料與粘彈性力學[M].北京:機械工業出版社，2011.

[14] MARCKMANN G，VERRON E，GORNET L.A theory of network alteration for the Mullins effect[J].Journal of The Mechanics and Physics of Solids，2002，50:2011-2028.

[15] Bischoff J E，Arruda E M，K GROSH.A new constitute model for the compressibility of elastomers at finite deformations[J].Rubber Chemistry and Technology，2001，74(3):541-559.

[16] PENN R W.Volume changes accompanying the extension of rubber[J].Transactions of The Society of Rheology，1970，14(4):509-517.

[17] GRAESSER E J，GOZZARELLI F A.A multidimensional hysteretic model for energy absorbing devices[R].New York:NCEER,1991:1-76.

[18] 李曉芳,楊曉翔.橡膠材料的超彈性本構模型[J].彈性體，2005，15(1):50-58.

[19] 曉芳.橡膠鋼雙材料非線性有限元分析及破壞機理研究[D].福州：福州大學，2006.

[20] 黃筑平.連續介質力學基礎:第二版[M].北京：高等教育出版社,2012.

[21] BOYCE M C，ARRUDA E M.Constitute models of rubber elasticity:a review[J].Rubber Chemistry and Technology，2000，73(3):504-522.

[22] MOONEY R A.Theory of large elastic deformation[J].Appl Phys，1940，11(9):582-592.

[23] ODGEN R W.Large deformation isotropic elasticity on the correlation of theory and experiment for incompressible rubberlike solids[J].Proc R Soc Lond Ser A，1972，328(1575):567-583.

[24] ODGEN R W.Nearly isotropic elastic deformations:application to rubberlike solids[J].Journal of The Mechanics and Physics of Solids，1978，26(1):37-57.

[25] ODGEN R W，Roxburgh D G.A pseudo-elastic model for the Mullins effect in filled rubber[J].Proc R Soc Lond Ser A,1999,455(1988):2861-2877.

[26] YEOH O H.On the ogden strain energy function [J].Rubber Chemistry and Technology，1992，65(3):51-67.

[27] TSAI C S，CHIANG T，CHEN B，et al.An advanced analytical model for high damping rubber bearings[J].Earthquake Engineer& Structural Dynamics，2003，32(9):1373-1387.

[28] AHMADI H R，KINGSTON J G R，MUHR A H，et al.Interpretation of high-low-strain modulus of filled rubbers as an inelastic effect [C]//Proc.,3rd European Conf.on Constitutive Models for Rubbers.Busfield and A Muhr,eds Balkema,Rotterdam.The Netherlands：CRC Press/Balkema，2003:357-364.

[29] 袁涌，魏威，譚平，等.一種基于改進超彈性Zener模型的高阻尼橡膠隔震支座速度相關性本構模型[J].土木工程學報，2016，49(3):72-79.

[30] 康國政,蔣晗,闞前華.連續介質力學:基礎和應用[M].北京:科學出版社,2014.