集裝箱港區疏港道路信號控制交叉口通行能力研究

唐國磊，劉翰卿，王文淵

(大連理工大學 建設工程學部，遼寧 大連 116024)

集裝箱港區疏港道路信號控制交叉口通行能力研究

唐國磊，劉翰卿，王文淵

(大連理工大學 建設工程學部，遼寧 大連 116024)

通過建立微觀交通仿真模型分析大車混入時飽和流率值和相位損失時間的變化規律，進而推求疏港道路信號控制交叉口通行能力。分析仿真結果發現飽和流率值與大車率呈反比例函數關系，相位損失時間與大車率呈二次函數關系。實例表明：與實際通行能力值相比，采用文中提出的計算方法所得值誤差較小，說明該方法合理有效。

交通運輸工程；疏港道路；通行能力；飽和流率；相位損失時間

0 引 言

港口集疏運系統是與港口相互銜接、主要為集中與疏散港口吞吐貨物服務的交通運輸系統，是港口賴以存在與發展的主要外部條件。因此，規劃設計集裝箱港區疏港道路信號控制交叉口時，合理確定信號控制交叉口的通行能力成為亟待解決的問題之一。然而，集裝箱港區疏港道路交叉口交通流中，大型車(集裝箱卡車)混入比率高，與以小汽車為主的城市道路交通流有顯著差異，現行《城市道路交叉口規劃規范》不再適用，有必要研究不同大車混入率(下稱大車率，HV)下信號控制交叉口通行能力。

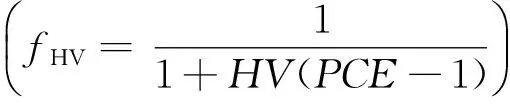
以上對車輛換算系數、大車修正系數和相位損失時間的討論，主要適用于城市道路中大車率較小的情況，并不完全適用于大車率較高的集裝箱港區疏港道路信號控制交叉口通行能力求算。因此，通過建立微觀仿真模型，以探求疏港道路交叉口通行能力與不同大車率之間的關系。

1 信號控制交叉口通行能力

GB 50647—2011《城市道路交叉口規劃規范》規定，信號控制交叉口進口車道的通行能力(CAPi)應由車道規劃飽和流量(Si)與進口車道所屬信號相位的綠信比(λi)相乘得到：

CAPi=Si·λi=S0·fHV·λi

(1)

其中，規劃飽和流量(Si)應結合進口車道大車率，對基本飽和流量(S0)進行修正確定。規劃飽和流量即飽和流率，是假定信號交叉口引道在全綠條件下(即綠信比為1)所能通過的最大流量。當大車率較大時，飽和流率值將大幅降低，因此有必要對大車修正系數(fHV)進行研究。

由于集裝箱卡車車身長、機動性差，加減速性能明顯不如小汽車，大車混入時，信號相位損失時間將會顯著提高，綠信比將顯著減小。

依上所述，疏港道路信號控制交叉口通行能力的確定可歸結于對飽和流率值(亦即基本飽和流量、大車修正系數)和信號相位綠信比(亦即相位時長、相位損失時間)的確定，其計算圖如圖1所示。下文將通過建立微觀交通仿真模型來分析大車混入時飽和流率值和相位損失時間值的變化規律。

2 微觀交通仿真模型建立

微觀交通仿真軟件VISSIM中車輛的縱向運動(跟車模型)采用Wiedemann建立的生理-心理駕駛行為模型，橫向運動(車道變換)采用基于規則的算法[7]。Wiedemann的生理-心理駕駛行為模型是迄今用于計算機交通仿真的最為精確的模型之一，因此VISSIM能較真實反映和重現實際交通狀況，在微觀交通仿真領域得到了廣泛應用[8]。筆者基于VISSIM對疏港道路信號控制交叉口進行微觀交通仿真研究，通過分析仿真結果，挖掘大車混入時疏港道路交叉口飽和流率值和相位損失時間的變化規律。

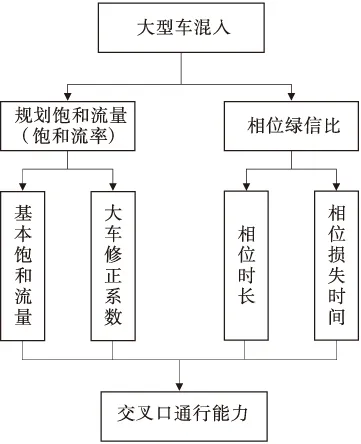
圖1 疏港道路信號控制交叉口通行能力求算圖Fig.1 The chart of calculating traffic capacity of signalized intersections on collection and distribution road

2.1 仿真模型建立

基于某疏港道路信號控制交叉口建立微觀仿真模型。該交叉口進口道路面平坦，無縱坡，車道寬度為3.75 m，左轉車道轉彎半徑約40 m，右轉車道轉彎半徑約25 m(道路幾何參數為理想狀態)。改變大車混入率時，車道寬度、轉彎半徑、有無縱坡等道路幾何參數并不會對交叉口通行能力的改變產生顯著影響，下文不再贅述。

2.2 車輛類型

通過調研集裝箱疏港道路信號控制交叉口處交通情況，確定模型中車輛仿真參數：交通流主要由小汽車(標準車)和集裝箱卡車(大型車)組成，選取上述兩種車型作為微觀交通仿真輸入車型；小汽車和集裝箱卡車的主要性能參數見表1，小汽車期望車速為40～50 km/h，集裝箱卡車的期望車速為30～40 km/h。

表1 車輛主要性能參數Table 1 Main vehicle performance parameters

2.3 駕駛行為參數

為使微觀交通仿真模型能正確反映現實交通狀況，需正確標定模型中的跟馳參數和車道變換參數，它們將深刻影響仿真模型的準確性。選用的跟車模型為Wiedemann 74模型，橫向運動選用自由車道選擇方式[7]，經校正后車輛的跟馳參數和車道變換參數的標定值見表2[8-11]。

表2 仿真模型參數標定Table 2 Calibrated parameters of the simulation model

2.4 駕駛行為參數標定

采用以下方法對模型參數進行校核與驗證：將仿真獲得的穩定流車頭時距數據與實測數據,進行比較，并對其進行t分布假設檢驗。

基于t分布假設檢驗，建立假設H0：假設微觀仿真測得的平均車頭時距與實測得到的平均車頭時距相等。由t檢驗結果得到，在95%的置信水平下，微觀仿真測得的平均車頭時距與實測平均車頭時距并無顯著差異，如表3。因此可以認定采用文中建立的微觀仿真模型進行交通仿真所得結果合理有效[12]。

表3 95 %置信度水平下車頭時距t檢驗結果Table 3 “ t ” test of time headway on the confidence level up to 95%

3 通行能力分析

3.1 交叉口飽和流率

根據飽和流率的定義將交叉口某方向進口道信號相位設為全綠(其他方向禁行)，改變交通流構成(即大車率)，運行仿真模型得到不同大車率下該交叉口進口道直行車道的最大交通量，即飽和流率，如表4。

表4 不同大車率下信號控制交叉口飽和流率Table 4 Saturation flow of signalized intersections on different mix rate of heavy vehicle

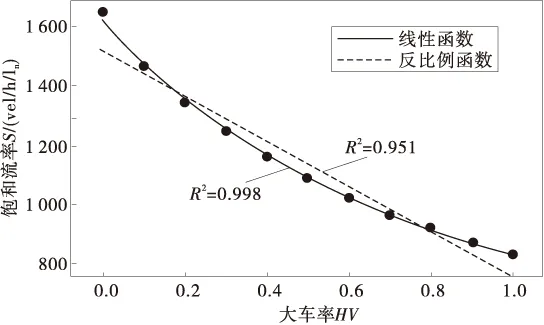
圖2 大車率-飽和流率擬合曲線Fig.2 Fitting curves of saturation flow and mix rate of heavy vehicle

如圖2，分別用線性函數和反比例函數對表1的數據進行擬合，發現采用反比例函數要比線性函數擬合效果好。因此，求算交叉口飽和流率時，采用反比例函數對大車進行修正更為合理。圖2中反比例函數擬合公式為

(2)

進一步仿真發現，對于左轉車道、右轉車道、直左共用車道以及直右共用車道，飽和流率值與大車混入率也呈反比例函數關系(左轉車道飽和流率值S=1 600×1/(1+1.15HV)，右轉車道飽和流率值S=1 570×1/(1+1.08HV)，直左、直右共用車道飽和流率值與直行車道飽和流率值相近)。

3.2 相位損失時間

假設某進口車輛可通行相位為P，改變大車混入率和相位P的相位時長(30,40,50,60,70 s)，仿真可得當相位P累計占用時間為1 h時，該交叉口進口道通過的車流量，如圖3。

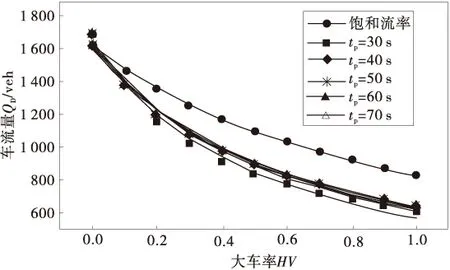
圖3 信號控制交叉口大車率-車流量關系Fig.3 Relational graph of traffic volume and mix rate of heavy vehicle on signalized intersections

由圖3可以發現，大車率越大、相位時長越小，交叉口通行能力越小。其原因主要是大車加減速性能較差，在綠燈信號控制初期和末期通行流率顯著降低，導致相位損失時間加大，有效綠燈時間和綠信比逐漸減小。集裝箱卡車混入時，相位損失時間與大車混入率、信號相位時長的關系如圖4。

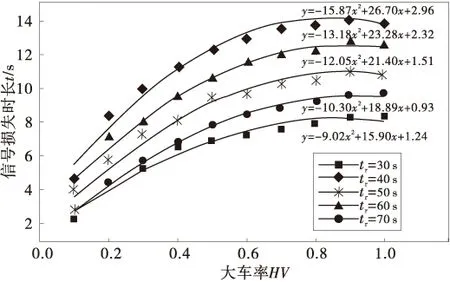
圖4 大車率、信號相位時長與相位損失時間關系Fig.4 Relationship between phase lost time and mix rate of heavy vehicle or phase time

由圖4可以看出，大車率增大時，相位損失時將從2 s快速增加至10 s以上，相位損失時間與大車率呈二次函數關系。而且，相位損失時間與相位時長有關，相位時間越長，相位損失時間越多，這是由于大小車性能不一致，車輛之間的相互干擾始終存在造成的。

4 應用實例

某集裝箱港區疏港道路十字交叉口(如圖5)各方向進口道均為雙車道，信號相位為兩相位(東西向相位時長40 s，南北向相位時長60 s)，東西向車種比例小汽車：集卡為4∶1，南北向車種比例小汽車：集卡為2∶3，道路無縱坡，道路幾何參數處于理想狀態，試求該交叉口的通行能力。

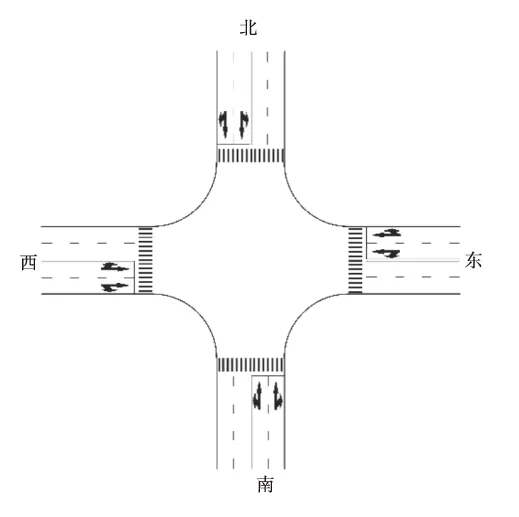
圖5 交叉口平面Fig.5 Plane of road intersection

根據式(1)、式(2)及圖4，分別計算東西向、南北向的進口道通行能力。以東西向為例，該交叉口東西向進口道通行能力為:

1)飽和流率為

2) 由圖4可得，相位損失時間為

t1=-10.30×0.22+18.89×0.2+0.93=4.3s

綠信比為

φ1=(40-4.3)/100=0.36

3) 所以，東西向進口道通行能力為

CAP東，西=1 340×0.36×2=965veh/h

同理，南北向進口道通行能力為

CAP南，北=953veh/h

則該交叉口通行能力為

CAP=965×2+953×2=3 836veh/h

實際調研該進口道通行能力約為3 600veh/h。若采用《城市道路交叉口規劃規范》規定的通行能力計算方法，則該交叉口通行能力CAP=1 443veh/h，計算所得值嚴重偏小，與實際不符。相比之下，由筆者提出的計算方法與實際值相比相對誤差較小，說明該方法求算疏港道路交叉口處通行能力合理有效。

5 結 語

當大型車混入時，將對疏港道路交叉口通行能力產生顯著影響。通過建立微觀仿真模型，分析得出了大車混入下飽和流率值和相位損失時間值的變化規律，并給出了疏港道路信號交叉口通行能力的求算方法。得出以下結論：疏港道路交叉口飽和流率可以通過大車修正系數求得，大車修正系數采用反比例函數比較合適；大車加減速性能對疏港道路交叉口通行能力影響顯著，大車混入時，相位損失時間顯著增大，相位損失時間與大車率呈二次函數關系。

[1] 同濟大學. 城市道路交叉口規劃規范：GB50647-2011[S]. 北京: 中國計劃出版社, 2011.TongjiUniversity. Code for Planning of Intersections on Urban Roads：GB50647-2011[S].Beijing:ChinaPlanningPress, 2011.

[2] 陳洪仁, 楊龍海, 李麗蘭. 基于速度和車頭時距的車輛換算系數計算方法研究[J]. 哈爾濱建筑大學學報,2001,34(2):110-114. CHEN Hongren, YANG Longhai, LI Lilan. Analysis of vehicle conversion factor[J].JournalofHarbinUniversityofCivilEhgineering&Architecture,2001,34(2):110-114.

[3] 中交第一公路勘察設計研究院.公路路線設計規范：JTG D20 2006[S]. 北京: 人民交通出版社, 2006. CCCC First Highway Consultants Co., Ltd..DesignSpecificationforHighwayAlignment：JTG D20 2006[S]. Beijing: China Communications Press, 2006.

[4] Transportation Rsearch Board.HighwayCapacityManual2000[S]. Washington, D.C.: National Research Council, 2000.

[5] 陳錦秀, 陳小鴻, 林航飛. 《城市道路平面交叉口規劃與設計規程》基本飽和流量與大車校正系數檢驗研究[J]. 城市交通,2004,2(3):17-20. CHEN Jinxiu, CHEN Xiaohong, LIN Hangfei. Research on verifyingbase saturation flow and heavy vehicle adjust factor in design rugulation for at-grade intersections on urban street[J].UrbanTransportofChina,2004,02(03):17-20.

[6] 王殿海, 楊少輝, 景春光. 累計曲線法計算飽和流率和相位損失時間[J]. 交通運輸工程學報,2003,3(3):75-78. WANG Dianhai, YANG Shaohui, JING Chunguang. Cumulative curve method for calculating saturation flow rate and phase lost time[J].JournalofTrafficandTransportationEngineering, 2003, 3(3):75-78.

[7] PTV.VISSIM4.30UserManual[M]. Karlsruhe: Plannning Transport Verkeher AG, 2007.

[8] 羅美清, 雋志才. VISSIM在交叉口交通設計與運行分析中的應用[J]. 武漢理工大學學報(交通科學與工程版),2004,28(2):232-235. LUO Meiqing, JUAN Zhicai. Application of VISSIM to transportation design and operation analysis of intersection[J].JournalofWuhanUniversityofTechnology(TransportationScience&Engineering),2004,28(2):232-235.

[9] 孫劍, 楊曉光, 劉好德. 微觀交通仿真系統參數校正研究[J]. 系統仿真學報,2007,19(1):48-50. SUN Jian, YANG Xiaoguang, LIU Haode. Study on microscopic traffic simulation model systematic parameter calibration[J].JournalofSystemSimulation, 2007, 19(1):48-50.

[10] 杜攀峰, 金雙泉, 李嘉. 高速公路路段通行能力仿真研究[J]. 湖南大學學報(自然科學版),2009,36(6):7-12. DU Panfeng, JIN Shuangquan, LI Jia. Simulation analysis of expressway capacity[J].JournalofHunanUniversity(NaturalScience),2009,36(6):7-12.

[11] 李志明, 閆小勇. 基于遺傳算法的交通仿真模型參數校正方法研究[J]. 交通標準化,2006(4):21-23. LI Zhiming, YAN Xiaoyong. Study on correction method of traffic simulation model based on genetic algorithm[J].CommunicationsStandardization,2006(4):21-23.

[12] 吳志洲, 范宇杰, 張劍橋. 考慮集卡影響的上匝道合流區通行能力模型[J].同濟大學學報(自然科學版),2013,41(5):670-675. WU Zhizhou, FAN Yujie, ZHANG Jianqiao. Model of merge capacity under impact of container trucks[J].JournalofTongjiUniversity(NaturalScience),2013,41(5):670-675.

Traffic Capacity of Signalized Intersections on Collection and Distribution Road of Container Port

TANG Guolei，LIU Hanqing，WANG Wenyuan

( Faculty of Infrastructure Engineering，Dalian University of Technology，Dalian 116024，Liaoning P.R.China)

The function relationships between saturation flow rate and the phase lost time at the time of entering of large truck was analyzed through the establishment of microscopic traffic simulation model to further obtain the traffic capacity at signal-controlled intersection of port road. The results of simulation reveal that the saturation flow value and heavy truck rate is in the functional relationship of inverse proportion while the phase lost time value and rate of heavy trucks is in quadratic function relationship. Practical examples show that the calculated value resulted by the method proposed is very close to the actual traffic capacity value without little deviation, which justifies the rationality and effectiveness of this given method.

traffic and transportation engineering;collection and distribution road； traffic capacity；saturation flow；phase lost time

10.3969/j.issn.1674-0696.2016.04.26

2015-04-20；

2015-08-09

國家自然科學基金項目(51309049，51109030)

唐國磊(1980—)，男，山東煙臺人，副教授，博士，主要從事港口規劃、港口系統仿真優化等方面的研究。E-mail:tangguolei@dlut.edu.cn。

劉翰卿(1990—)，男，江蘇鹽城人，碩士研究生，主要從事港口規劃、港口系統仿真優化等方面的研究。E-mail:liuhanqingdlut@163.com。

U651

A

1674-0696(2016)04-133-04