S-可除模及S-Dedekind環

高玉兵, 王芳貴, 熊 濤

(四川師范大學 數學與軟件科學學院, 四川 成都 610066)

S-可除模及S-Dedekind環

高玉兵, 王芳貴*, 熊 濤

(四川師范大學 數學與軟件科學學院, 四川 成都 610066)

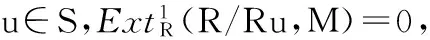
S-正則理想;S-可除模;S-正則內射模;S-Noether環;S-Dedekind環

1 預備知識

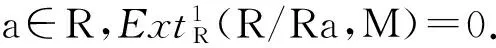
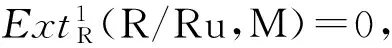
最后,本文恒設R是有單位元的結合環,若無特別指定,所有的模均指左模.對R-模M,E(M)表示M的內射包絡.其他未指明的環與模的概念和符號,可以參見文獻[13].

2 S-可除模

盡管傳統的可除模的研究主要放在交換環上,但為了使結論對非交換環起作用,以下假設R可以是非交換環,S是包含在R的中心內的非零因子乘法封閉集.

定義 2.1 設M是R-模.

1) 令tor(M)={x∈M|存在u∈S,使得ux=0},這是M的子模,稱為M的完全S-撓子模.此外,若tor(M)=M,則M稱為S-撓模;若tor(M)=0,則M稱為S-無撓模;

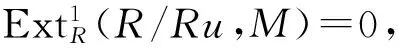
例 2.2 下面的事實是顯然的:

1) 內射模和FP-內射模都是S-可除模;

2)S-撓模的子模與商模都是S-撓模;

3)S-無撓模的子模是S-無撓模;

4) 若M是S-無撓模,則E(M)是S-無撓模;

5) 若N是任何模,M是S-無撓模,則HomR(N,M)是S-無撓模;

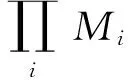
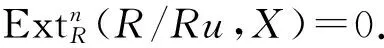
證明 設M是S-可除模,則n=1時斷言是成立的.由于u不是R的零因子,故pdRR/Ru≤1，因此當n≥2斷言也是成立的.

反之是顯然的.

命題 2.4 對任何R-模M,以下等價:

1)M是S-可除模;

2) 對任何u∈S,0→HomR(R/Ru,M)→HomR(R,M)→HomR(Ru,M)→0是正合列;

3) 設A是R-模B的子模,f:A→M是同態.若存在u∈S,使得B/A?R/Ru,則0→HomR(B/A,M)→HomR(B,M)→HomR(A,M)→0是正合列;

4) 設A是R-模B的子模,f:A→M是同態.若存在u∈S,使得B/A?R/Ru,則同態f可以擴張到B;

5) 設0→M→B→C→0是正合列.若存在u∈S,使得C?R/Ru,則該正合列分裂.

證明 1)?2)和1)?4)?3)顯然.

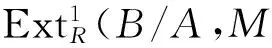
1)?5) 由文獻[13]的定理4.5.4(3)即得.

命題 2.5S-可除模的正向極限是S-可除模.

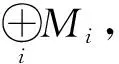
定義 2.6 設M是R-模,

1) 若由x∈E(M),u∈S,ux∈M,能推出x∈M,則M稱為S-可約模;

2) 令S(M)={x∈E(M)|存在u∈S,使得ux∈M},稱之為M的S-可除包絡.

例 2.7 設u∈R是非零因子,S={un|n≥0},則S(Ru)=S(R)=Ru.

命題 2.8 設M是R-模,

1)M是S-可約模當且僅當E(M)/M是S-無撓模;

2)S(M)是S-可約模;

3) 若M是S-可約模,則M是S-可除模,從而S(M)是S-可除模.

證明 1) 顯然.

3) 設u∈S,f:RuM是同態,則存在同態g:RE(M),使得對g(u)=ug(1)=f(u)∈M.由于M是S-可約模,故有x∈M,即Im(g)?M.因此有g:R→M是f的擴張.故M是S-可除模.

定理 2.9 設M是S-無撓的S-可約模,N是M的子模,則N是S-可約模當且僅當由x∈M,u∈S,ux∈N能推出x∈N.

證明 必要性 設N是S-可約模,由于N是M的子模,可設E(N)?E(M),于是有E(M)=E(N)⊕A,其中A是E(M)的子模.記x=y+z,y∈E(N),z∈A.對任何u∈S,有uz=ux-uy∈N∩A,因此uz=0.由于M是S-無撓模,由例2.2知E(M)也是S-無撓模,故得到z=0,因此x∈E(N).再由N是S-可約模的定義知x∈N.

充分性 設x∈E(N),u∈S,ux∈N.由M是S-可約模及x∈E(M),有x∈M,由條件,故N是S-可約模.

3 S-正則內射模

設I是R的左理想.若I∩S≠?,則稱I是S-正則左理想.容易看到,若I是S-正則左理想,則R?S(I).文獻[15]定義了正則內射模的概念,相應地,本文也引入S-正則內射模的概念.

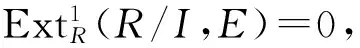
例 3.2 下面的事實也是顯然的.

1) 內射模是S-正則內射模;

2)S-正則內射模是S-可除模;

例如：教師可以以開展比賽的活動，來培養學生敢于探索、敢于創新的優秀品質。教師可以要求學生十個人為一組，兩個人甩繩，八個人跳繩，然后集體跳繩，看看哪個組跳的多并且又具有創新性，通過這樣的方式來培養學生敢于探究、敢于創新的美好品質。二十一世紀的我們，不僅需要學生加強體育運動，還要求學生努力探索、努力創新，以最有效率的學習方法來提升自己，努力做到以學生為本的教育理念。因此，開展跳繩運動就顯得非常有必要，教師一定要學會調動學生的積極性，讓學生主動探究。

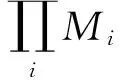
4) 設0→A→B→C→0是正合列,且A和C都是S-正則內射模,則B也是S-正則內射模.

定理 3.3 對R-模E,以下各條等價:

1)E是S-正則內射模;

2) 對R的任何S-正則左理想I,任何同態f:I→E能擴張到R上;

3) 設A是R-模B的子模,f:A→E是同態.若B/A是S-撓模,則f可以擴張到B;

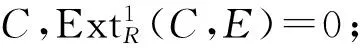
5) 設A是R-模,f:A→E是同態,則f可以擴張到S(A).

證明 1)?2)和3)?4)顯然.

2)?3) 設f:A→E是同態,令

Γ={(C,d)|C是B中包含A的子模,

且d是f在C上的擴張}.

類似于Baer準則的證明,Γ中有極大元,設為(C,d).下證C=B,從而斷語成立.

若C≠B,取x∈B-C.令I={r∈R|rx∈C},則I是R的左理想.由于B/A是S-撓模,故存在u∈S,使得ux∈C.因此I是S-正則左理想.令h:I→E,使對r∈I,h(r)=d(rx).由條件,有同態g:R→E,使得h(r)=g(r),r∈I.令C1=C+Rx,d1:C1→E,使d1(c+rx)=d(c)+g(r),c∈C,r∈R.若c+rx=0,則r∈I,從而d(c)+g(r)=d(c)+d(rx)=d(c+rx)=0.故d1是完全確定的同態,且是d的擴張，因此(C1,d1)∈Γ,這與(C,d)的極大性矛盾.

3)?2)和3)?5)顯然,因為R/I和S(A)/A都是S-撓模.

5)?2) 設I是R的正則左理想,f:I→E是同態.由條件,存在f可以擴張為h:S(I)→E.由于R?S(I),故同態g=h|R就是f的擴張.

定理 3.4 對S-無撓模E,以下各條等價:

1)E是S-正則內射模;

2)E是S-可除模;

3)E是S-可約模.

證明 1)?2) 顯然.

2)?3) 設E0是E的內射包,x∈E0,u∈S,ux∈E.定義f:Ru→E,使得f(ru)=rux.由于E是S-可除模,故存在同態g:R→E,使得g(u)=f(u)=ug(1)，因此有u(x-g(1))=0.由例2.2的4),E0是S-無撓模,故有x=g(1)∈E,即E是S-可約模.

3)?1) 設I是R的S-正則理想,f:I→E是同態,則存在同態g:R→E0,使得下圖可交換

↑f↑g

設u∈I∩S,則ug(1)=g(u)=f(u)∈E.由于E是S-可約模,故g(1)∈E,即g:R→E是f的擴張,故E是S-正則內射模.

命題 3.5 設0→A→M→B→0與0→A→M′→C→0是正合列,其中M是S-正則內射模,C是S-撓模,則有正合列0→M′→M⊕C→B→0.

證明 由定理3.3,存在同態g:M′?M,使得下圖是行正合的交換圖

‖ ↓g↓g1

其中g1是左邊方圖的誘導同態.由此得到0→M′→M⊕C→B→0是正合列.

4 S-Noether環

定義 4.1 環R稱為(左)S-Noether環,是指每個S-正則左理想都是有限生成的.

定理 4.2 對環R,以下各條等價:

1)R是S-Noether環;

2)R有S-正則左理想的升鏈條件;

3)R有S-正則左理想的極大條件.

證明 1)?2) 設M1?M2?…?Mn?…是R的S-正則左理想升鏈.令N=∪Mi.由條件N是有限生成的S-正則左理想.記N=Rx1+…+Rxk.故存在m,使得對一切i,xi∈Mm,從而有N?Mm.于是當n≠m時,Mn=Mm.

2)?3) 設Γ是R的S-正則左理想的非空集合.若Γ中無極大元,任取M1∈Γ,則M1不是極大元素.故有M2∈Γ,使得M1?M2.同理M2也不是極大元素,故又可找M3∈Γ,使得M2?M3.如此下去,于是得到R的一個S-正則左理想升鏈M1?M2?…?Mn?…,該鏈不是穩定的,這與給定的條件矛盾.因此Γ中有極大元.

3)?1) 設N是R的S-正則左理想,令Γ={A?N|A是有限生成的S-正則左理想}.取u∈N∩S,則Ru∈Γ,故Γ非空,因此Γ有極大元A.若A≠N,則存在x∈N-A,于是A1=A+Rx是N的有限生成S-正則左理想且真包含A,這與A的選擇的極大性矛盾,因此N=A是有限生成的S-正則左理想.故R是S-Noether環.

定理 4.3 設R是交換環,則R是S-Noether環當且僅當R的任何S-正則素理想是有限生成的.

證明 必要性 顯然.

充分性 設Γ是R的非有限生成S-正則左理想的集合.若Γ非空,由Zorn引理,Γ中有極大元p.設a,b∈R,使得ab∈p.若a?p,且b?p,令J={r∈R|ra∈p},則b∈J.于是p?p+Ra,p?J,因此p+Ra與J都是有限生成的.設{p1+r1a,…,pn+rna}是p+Ra的生成系,p1,…,pn∈p,r1,…,rn∈R,及{x1,…,xm}是J的生成系.類似于文獻[13]中定理1.2.5,可以證明p是有限生成的,這與p的選擇矛盾.故Γ為空集,從而R是S-Noether環.

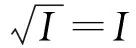
定理 4.4 設R是交換S-Noether環,則任何S-正則根理想是有限個(S-正則的)素理想的交.

證明 反設I是S-正則根理想,但I不是有限個素理想的交.令

是根理想,

但A不是有限個素理想的交},

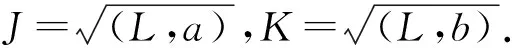
顯然L?J∩K.設x∈J∩K,則存在正整數m,n,使得xm∈J,xn∈K.記xm=i1+ya,xn=i2+zb,其中,i1,i2∈L,y,z∈R,所以

xm+n=(i1+ya)(i2+zb)=

i1i2+i1zb+i2ya+yzab∈L.

于是xm+n∈L,故x∈L.因此J∩K?L.于是得到L=J∩K,即L可以表示為有限個素理想的交,這與假設矛盾,故原結論成立.

定理 4.5 設R是交換S-Noether環,I是R的S-正則理想,則I上只有有限個極小素理想.

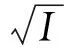
5 S-Dedekind

定義 5.1 環R稱為(左)S-遺傳環,是指每個S-正則左理想都是投射模.

定理 5.2 對環R,以下各條等價:

1)R是S-遺傳環;

2)S-正則內射模的商模是S-正則內射模;

3) 內射模的商模是S-正則內射模;

4) 設P是投射模,M是P的子模.若P/M是S-撓模,則M是投射模;

5) 設P是投射模,M是P的子模,且I={r∈R|rP?M}是S-正則左理想,則M是投射模;

6) 對任何S-撓模C,pdRC≤1.

證明 2)?3)和4)?6)顯然.

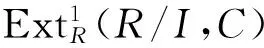
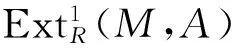
4)?5) 顯然,因為此時的P/M是S-撓模.

5)?1) 設I是R的S-正則左理想.對P=R,M=I應用給定的條件得到I是投射模.故R是S-遺傳環.

設R是交換環,用T(R)表示R的完全商環,即T(R)中的元素可以表示為r/s,其中r∈R,s是R的非零因子.注意r/s是T(R)的非零因子當且僅當r是R的非零因子.設A是T(R)中的R-子模,稱A是正則的,是指A包含T(R)中的一個非零因子.

對T(R)的任何R-子模A,定義

A-1={x∈T(R)|xA?R},

則顯然A-1還是T(R)的R-子模.若存在T(R)的R-子模B,使得AB=R,則A稱為可逆的.此時必有B=A-1.因此A是可逆的當且僅當AA-1=R.

引理 5.3 設A是T(R)的R-子模,則有:

1) 若A是可逆的,則A是有限生成的;

2) 若A是正則的,則A是投射模當且僅當A是可逆的.

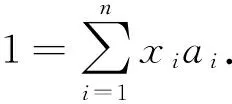
2) 必要性 設A是投射模.設{ai,fi|i∈Γ}是A的投射基.由于A是正則的,存在正則元b∈A,不妨設b=r1/t1.t1∈S,r1∈R.對任何的a∈A,不妨設a=r/t,t∈S,r∈R.由

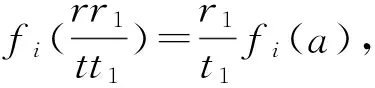
所以

又因為b是正則元,故

即有AA-1=R.從而A可逆.

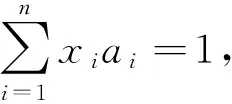
因此,A有投射基{a1,…,an,f1,…,fn},故A是投射模.

設a∈R,若存在r∈R,及s∈S,使得s=ra,則a稱為擬S-正則元素.顯然,當S是飽和乘法集時,擬S-正則元全在S中.

例 5.4 設R=Z,S={4n|n≥0},則2是擬S-正則元素,但不在S中.

引理 5.5 設R是交換環,I是R的S-正則理想.若I是主理想,則I可由一個擬S-正則元素生成.

證明 設I=(a).取s∈I∩S,則s=ra,r∈R.因此,a是S-正則元素.

定義 5.6 設R是交換環.若R的每個S-正則理想都是可逆的,則R稱為S-Dedekind環.若每個S-正則理想是主理想,則R稱為S-主理想環.

當S是R的所有非零因子乘法集時,此時的S-Dedekind環就是諸多文獻提到的Dedekind環.當R是整環,S=R-0時,則S-Dedekind整環就是眾所周知Dedekind整環,S-主理想環就是主理想整環.

定理 5.7 設R是S-Dedekind環,則R是S-Noether環,且每個S-正則素理想是極大理想.

證明 由引理5.3,R是S-Noether環.設I是R的S-正則素理想.若I不是極大理想,則存在S-正則素理想J,使得IJ.令K=J-1I.因為I?J,則K?J-1J=R.又因為JK=I,JI,以及I是素理想,有K?I.由I=JK?JIRI=I,矛盾.所以I是極大理想.

定理 5.8 設R是S-主理想環,則S-可除模是S-正則內射模.

證明 設E是S-可除模,I=(a)是S-正則理想,f:I→E是同態.設s∈I∩S,b∈R,使得s=ba.由于E是S-正則內射模,則存在x∈E,使得f(s)=sx=bax.令g:R→E,g(1)=x,則g(a)=ax,于是g是f的擴張,從而E是S-正則內射模.

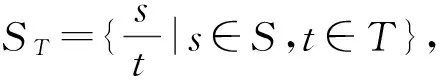
引理 5.9 設R是交換環,T是R的乘法集,I是R的有限生成的正則理想.記I(T)={x∈T(R)T|xIT?RT},則有:

1)I(T)IT?RT,且I(T)=(I-1)T;

2) 若I是S-正則理想,且IT=aRT/t是主理想,則ITI(T)=RT.

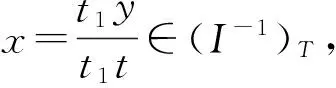
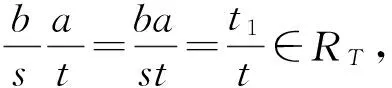
引理 5.10 設R是交換環,

1)I是R的S-正則真理想,則存在R的S-正則極大理想m,使得I?m;

2) 若A、B是R的S-正則理想,則A=B當且僅當對R的S-正則理想極大理想m,記T=R-m,有AT=BT.

證明 1) 顯然.

2) 必然性是顯然的,下證充分性.設a∈A,令I={r∈R|ra∈B},則I是R的理想.取u∈B∩S,則ua∈B,故u∈I,即I是S-正則理想.設m是R的S-正則極大理想,T=R-m.由于AT=BT,故存在t∈T,使得ta∈B,故Im.由1)有I=R.故1∈I.于是a=1a∈B,即A?B.同理,B?A.于是得到A=B.

定理 5.11 設R是交換環,則以下各條等價:

1)R是S-Dedekind環;

2)R的任何S-正則極大理想m,記T=R-m,有RT是ST-主理想環;

3) 對R的任何S-正則素理想P,P是可逆理想.

證明 1)?2) 設A是RT的ST-的正則理想.令I={a∈R|a/1∈A},則I是R的S-正則理想,且A=IT.由于R是S-Dedekind環,I是投射理想,從而A=IT是投射RT模.因此A是主理想.故RT是ST-主理想環.

2)?1) 設I是R的S-正則左理想,則IT是RT的ST-正則理想.由條件,IT是主理想.由引理5.9,于是有ITI(T)=IT(I-1)T=(II-1)T=RT.由引理5.10有II-1=R,故I是可逆理想.從而有R是S-Dedekind環.

1)?3) 顯然.

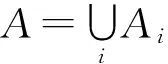
定理 5.12 設R是交換S-Dedekind環,E是R-模,則E是S-正則內射模當且僅當對R的任何S-正則極大理想m,記T=R-m,有ET是ST-正則內射RT-模.

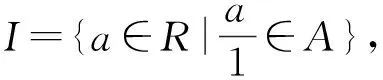
由于I是有限生成投射模,從而是有限表現模.故由文獻[13]中定理3.4.8知θ同構.故由5項引理θ1是同構.故有

因此ET是ST-正則內射模.

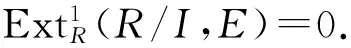
定理 5.13 設R是交換環,則以下各條等價:

1)R是S-Dedekind環;

2)R是S-遺傳環;

3) 每個S-可除模是S-正則內射模.

證明 1)?3) 設E是S-可除模.對R的任何S-正則極大理想m,令T=R-m.易見ET是ST-可除RT-模,由定理5.11,RT是ST-主理想環.由定理5.8,ET是ST正則內射RT模.由定理5.12,E是S-正則內射模.

3)?2) 設C是內射模的商模.自然地,C是S-可除模.由條件,C是S-正則內射模.由定理5.2知R是S-遺傳環.

2)?1) 設I是R的S-正則理想.由條件,I是投射模.由引理5.3,I是可逆的.故R是S-Dedekind環.

[1] SHARPE D W, VAMOS P. Injective Modules[M]. Cambridge:Cambridge University Press,1972.

[2] LEE S B. Weak-injective modules[J]. Commun Algebra,2006,34(1):361-370.

[3] FUCHS L, LEE S B. Weak-injectivity and almost perfect domains[J]. J Algebra,2009,321(1):18-27.

[4] FUCHS L, SALCE L. Modules over Valuation Domains[C]//New York:Lecture Notes in Pure and Applied Math,1985:97.

[5] LEE S B.h-Divisible modules over intergral domains[J]. J Algebra,2011,330(1):76-85.

[6] ENOCHS E E, JENDA O M G.h-Divisible and cotorsion modules over one-dimensional Gorenstein rings[J]. J Algebra,1993,161(2):444-454.

[7] FACCHINI A, BIEN M H. Injective modules and divisible modules over hereditary rings[J]. Unione Mat Ital,2015,7(4):299-308.

[8] HüGEL L A, HERBERA D, TRLIFAJ J. Divisible modules and localization[J]. J Algebra,2005,294(2):519-551.

[9] LEE S B.h-Divisible modules[J]. Commun Algebra,2003,31(1):513-525.

[10] MATLIS E. Divisible modules[J]. Proc Am Math Soc,1960,11(3): 385-391.

[11] FUCHS L, SALCE L. S-divisible modules over domains[J]. Forum Mathematicum,1992,4(4):383-394.

[12] MAO L X, DING N Q. On divisible and torsionfree modules[J]. Commun Algebra,2008,36(2):708-731.

[13] 王芳貴. 交換環與星型算子理論[M]. 北京:科學出版社,2006.

[14] ROTMAN J J. An Introduction to Homological Algebra[M]. London:Academic Press,1979.

[15] 王芳貴,廖家麗.S-內射模及S-內射包絡[J]. 數學學報,2011,54(2):271-284.

[16] 王芳貴,汪明義,楊立英. 交換環上的極大性內射模[J]. 四川師范大學學報(自然科學版),2006,33(1):1-9.

2010 MSC：16D50; 16E10; 16E30

(編輯 李德華)

S-divisible Modules andS-Dedekind Rings

GAO Yubing, WANG Fanggui, XIONG Tao

(College of Mathematics and Software Science, Sichuan Normal University, Chengdu 610066, Sichuan)

LetRbe a ring andMbe aR-module. LetSdenote the regular multiplicative closed set of the center inR. If Ext1R(R/Ru,M)=0, for any regular elementu∈S, thenMis called anS-divisible modules. A leftR-moduleEis called anS-regular injective if Ext1R(R/I,E)=0 for anyS-regular left idealI.Ris called anS-Notherian rings if everyS-regular left ideal inRis finitely generated. A commutative ring is called anS-Dedekind ring if everyS-regular ideal inRis invertible. In this paper, we discuss the basic properties ofS-Noetherian rings. WithS-divisible modules characterizedS-Dedekind rings, it is also shown thatRis anS-Dedekind rings if and only ifS-divisible modules areS-regular injective modules.

S-regular ideals;S-divisible modules;S-regular injective modules;S-Noetherian rings;S-Dedekind rings

2015-12-24

國家自然科學基金(11171240)和教育部博士點專項科研基金(20125134110002)

O154

A

1001-8395(2016)06-0783-07

10.3969/j.issn.1001-8395.2016.06.001

*通信作者簡介：王芳貴(1955—),男,教授,主要從事交換代數、同調代數與代數K-理論的研究,E-mail:wangfg2004@163.com