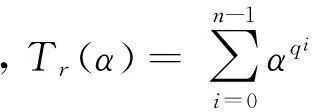有限域上(4,7)型高斯正規(guī)基及其對偶基的本原性
魏 杰, 廖群英, 周嘉駿
(四川師范大學(xué) 數(shù)學(xué)與軟件科學(xué)學(xué)院, 四川 成都 610066)
有限域上(4,7)型高斯正規(guī)基及其對偶基的本原性
魏 杰, 廖群英*, 周嘉駿
(四川師范大學(xué) 數(shù)學(xué)與軟件科學(xué)學(xué)院, 四川 成都 610066)
有限域上的正規(guī)基在編碼理論、密碼體制及信號傳遞等領(lǐng)域有著廣泛的應(yīng)用,本原正規(guī)基因其獨(dú)特的本原性質(zhì)更為重要.最近,文獻(xiàn)(魏杰,李雪連,廖群英. 四川大學(xué)學(xué)報(自然科學(xué)版),2016,53(1):7-12.)由k-型高斯正規(guī)基構(gòu)造定理,確定了Fq4在Fq上的7-型高斯正規(guī)基N及其對偶基B和跡基的準(zhǔn)確復(fù)雜度.進(jìn)一步研究N和B的本原性質(zhì),證明了有限域Fq特征為2或3時,N為本原正規(guī)基當(dāng)且僅當(dāng)q=2或q=3,此時B均不是本原正規(guī)基.
有限域; 高斯正規(guī)基; 對偶基; 本原元
1 主要結(jié)果
設(shè)q為素數(shù)p的方冪,n是正整數(shù),Fqn是有限域Fq的n次擴(kuò)域(n≥2),若N={α,αq,…,αqn-1}為Fqn在Fq上的正規(guī)基,則稱α為Fqn在Fq上的一個正規(guī)元.進(jìn)而令
則稱T=(ti,j)n×n為N的乘法表,T中非零元素的個數(shù)稱為N的復(fù)雜度,記為CN.由于T=(ti,j)中的非零元越少,Fqn中乘法運(yùn)算的計算量也就越小.R. Mullin等[1]證明了CN≥(2n-1),且當(dāng)CN=(2n-1)時,稱N為最優(yōu)正規(guī)基,進(jìn)而給出了兩類最優(yōu)正規(guī)基的構(gòu)造定理,分別為I型和II型最優(yōu)正規(guī)基,并猜想最優(yōu)正規(guī)基只有這2類.隨后,S. H. Gao[2]證明了這個猜想.從而尋找次優(yōu)的正規(guī)基也成了很重要的課題.A. Wassermann[3]將有限域Fqn在Fq上的最優(yōu)正規(guī)基的概念推廣到(n,k)-型高斯正規(guī)基,這正是一類低復(fù)雜度的正規(guī)基,并且(n,1)-型高斯正規(guī)基即為I型最優(yōu)正規(guī)基,q=2時的(n,2)-型高斯正規(guī)基即為II型最優(yōu)正規(guī)基.
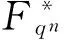
定理 1.1[4]對任意正整數(shù)n≥1和素數(shù)方冪q,Fqn在Fq上均存在本原正規(guī)基.
定理 1.2[5]對任意的素數(shù)方冪q,任意的正整數(shù)n(n≥2)以及任意的非零元素a∈Fq,都存在一個本原正規(guī)多項(xiàng)式f(x)=xn+c1xn-1+…+cn∈Fq[x],而且c1=a.
定理 1.3[6]對任意的素數(shù)方冪q,任意的正整數(shù)n(n≥15),任意的正整數(shù)m(1≤m 定理 1.4[7]對任意素數(shù)方冪q,任意正整數(shù)n(n≥2),除(q,n)取值為(2,3),(2,4),(3,4),(4,3),(5,4)外,都存在a∈Fq,使得α和α-1都是Fq上的本原正規(guī)元. 定理 1.5[8]對任意的素數(shù)方冪q,任意的正整數(shù)n(n≥7)以及任意的非零元素a,b∈Fq且a≠0,都存在一個本原正規(guī)多項(xiàng)式f(x)=xn+c1xn-1+…+cn∈Fq[x],且c1=a,c2=b. Q. Y. Liao[9]確定了所有的I型本原最優(yōu)正規(guī)基,并給出II型本原最優(yōu)正規(guī)基的一個充分條件. 另一方面,在有限域的眾多基中,對偶基也是一個很重要的概念.對于Fqn在Fq上的任意兩組基:B={βi=βqi|i=0,1,…,n-1}和N={αi=αqi|i=0,1,…,n-1},稱B為N的對偶基,若對任意的i,j=0,1,…,n-1,都有 定理 1.6[11]設(shè)q為素數(shù)p的方冪,N={α,αq,…,αqn-1}為Fqn在Fq上的k-型高斯正規(guī)基(1≤k≤n),則N的對偶基的生成元為 但是,有限域上本原正規(guī)基的對偶基不一定是本原正規(guī)基.迄今為止,人們只確定了最優(yōu)正規(guī)基的本原性,對于一般情形下的正規(guī)基,即使是性質(zhì)非常好的高斯正規(guī)基,其本原性的討論都很困難,可參考文獻(xiàn)[12-14].最近,文獻(xiàn)[15]給出了Fq4在Fq上的7-型高斯正規(guī)基及其對偶基和跡基的準(zhǔn)確復(fù)雜度.本文繼續(xù)文獻(xiàn)[15]的研究,進(jìn)一步完善文獻(xiàn)[15]的結(jié)果,由此給出有限域上一些新的本原高斯正規(guī)基,即證明了如下主要結(jié)果: 定理 1.7 設(shè)p為素數(shù),n為正整數(shù)且q=pn.設(shè)N={αi=αqi|i=0,…,3}為Fq4在Fq上的7-型高斯正規(guī)基,B={βi=βqi|1=0,…,3}為N的對偶基,其中α=α0,β=β0,則有: 1) 當(dāng)p=2時,N為本原正規(guī)基當(dāng)且僅當(dāng)q=2.此時B不是本原正規(guī)基; 2) 當(dāng)p=3時,N為本原正規(guī)基當(dāng)且僅當(dāng)q=3.此時B不是本原正規(guī)基. 以下引理2.2~2.4的證明可參見文獻(xiàn)[15]中定理1.2的證明. 引理 2.2[15]Fq4在Fq上的7-型高斯正規(guī)基N={αi=αqi|i=0,…,3}滿足: αα=2α+3α1+2α3; (1) αα1=α+α1+2α2+3α3; (2) αα2=7+2α+α1+2α2+α3; (3) αα3=α+2α1+3α2+α3. (4) 其中α=α0. 引理 2.3[15]設(shè)q為素數(shù)2的方冪,N={αi=αqi|i=0,…,3}為Fq4在Fq上的7-型高斯正規(guī)基,則N的對偶基B={βi=βqi|1=0,…,3}且 ββ=β1,ββ1=β3, ββ2=β+β1+β2+β3,ββ3=β2, 其中β=β0. 引理 2.4[15]設(shè)q為素數(shù)3的方冪,N={αi=αqi|i=0,…,3}為Fq4在Fq上的7-型高斯正規(guī)基,則N的對偶基B={βi=βqi|1=0,…,3}且 ββ=β3,ββ1=β2, ββ2=2β+2β1+2β2+2β3,ββ3=β1, 其中β=β0. 定理1.7的證明 1) 當(dāng)p=2時,由引理2.2知,此時(1)~(4)式等價于 αα=α1,αα1=α+α1+α3, αα2=1+α1+α3=α+α2, αα3=α+α2+α3. 因此可以得到 α2=α1,α3=αα1=α+α1+α3, α5=α2α3=αα1+α1α1+α1α3= αα1+(αα)q+(αα2)q=α+α2, 類似地 α8=α3α5=α3, α16=α3α3=(αα)q3=α, 進(jìn)而,再由引理2.3可知 β2=β1,β3=β3,β4=β2, β5=β+β1+β2+β3=Tr(β)=1. β的乘法階為5≠q4-1=15,即B不是本原正規(guī)基,這就證明了1). 2) 當(dāng)p=3時,由引理2.2可知,此時(1)~(4)式等價于 αα=2α+2α3,αα1=α+α1+2α2, αα2=1+2α+α1+2α2+α3=α+α2, αα3=α+2α1+α3, 此時有 α2=2α+2α3, α4=(2α+2α3)2= αα+(αα)q3+2αα3=α+α1+2α2, α5=2α+α1+α2+2α3, α8=α+α1+2α2+α3, α16=2α+α1+2α2+2α3, α9=α2,α10=α+α2, α20=α+2α1+α2+2α3, α40=α+α1+α2+α3=Tr(α)=-1, α80=1. 進(jìn)而,由引理2.4有 β2=β3,β3=β1,β4=β2, β5=2β+2β1+2β2+2β3=2Tr(β)=1. β的乘法階為5≠q4-1,B不是本原正規(guī)基.故定理1.7得證. 注 1 很多關(guān)于有限域上高斯正規(guī)基的復(fù)雜度和本原性的研究也只限于k值較小的情形,當(dāng)k≥8時問題就變得很困難.與文獻(xiàn)[15]討論具體(n,k)取值時相應(yīng)的高斯正規(guī)基的復(fù)雜度一樣,本文繼續(xù)討論該類型高斯正規(guī)基及其對偶基的本原性,給出了具體(n,k)值時的分類計算方式.但和復(fù)雜度不同的是,特征p≠2,3時,該類正規(guī)基的本原性的確定尚未得以解決. [1] MULLIN R, ONYSZCHUK I, VANSTONE S, et al. Optimal bases in GF(pm)[J]. Disc Appl Math,1988/1989,22(2):149-161. [2] GAO S H. Nomal bases over finite fields[D]. Ontario:Waterloo University,1993. [3] WASSERMANN A. Konstruktion von normal basen[J]. Bayreuther Mathematische Schriften,1990,31:155-164. [4] LENSTRA Jr II W, SCHOOF R J. Primitive normal bases for finite fields[J]. Math Comput,1987,48(177):217-231. [5] COHEN S D, HACHENBERGER D. Primitive normal bases with prescribed trace[J]. Appl Algebra Engrg Commun Comput,1999,9(5):383-403. [6] FAN S, WANG X. Primitive normal polynomials with a prescribed coefficient[J]. Finite Fields Appl,2009,15:682-730. [7] COHEN S D, HUCZYNSKA. The strong primitive normal basis theorem[J]. Acta Arith,2010,143(4):299-332. [8] FAN S Q, HAN W B, ZHANG X Y. Primitive normal polynomials with the first two coefficients prescribed:a revisedp-adic method[J]. Finite Fields Appl,2007,13:577-604. [9] LIAO Q Y. On primitive optimal normal elements of finite fields[J]. J Math Res Exp,2010,30(5):869-875. [10] MENEZES A J, BLAKE I F, GAO S H, et al. Applications of Finite Fields[M]. New York:Kluwer Academic Publishers,1993. [11] LIAO Q Y. The gaussian normal basis and its trace basis over finite fields[J]. J Number Theory,2012,132(7):1507-1518. [12] 李俊,黃琴,李波,等. 有限域上的k-型高斯正規(guī)基及其對偶基[J]. 四川師范大學(xué)學(xué)報(自然科學(xué)版),2011,34(3):289-295. [13] 廖群英,胡曉蘭. 有限域上一類高斯正規(guī)基的復(fù)雜度的準(zhǔn)確計算公式[J]. 數(shù)學(xué)學(xué)報,2014,57(5):863-874. [14] 蘇丹丹,廖群英. 有限域上一類特殊對偶基的推廣[J]. 四川大學(xué)學(xué)報(自然科學(xué)版),2011,48(1):27-32. [15] 魏杰,李雪連,廖群英. 有限域上的(4,7)型高斯正規(guī)基及其對偶基和跡基[J]. 四川大學(xué)學(xué)報(自然科學(xué)版),2016,53(1):7-12. [16] 廖群英,蘇丹丹,付萍. 有限域上2-型高斯正規(guī)基及其對偶基[J]. 四川大學(xué)學(xué)報(自然科學(xué)版),2010,47(6):1221-1224. [17] 廖群英,李雪連. 有限域上(n,k) (k≥3)型高斯正規(guī)基的對偶基的復(fù)雜度(英)[J]. 四川大學(xué)學(xué)報(自然科學(xué)版),2016,53(2):235-246. [18] 李雪連,廖群英. 偶特征有限域上一類高斯正規(guī)基的對偶基及跡基[J]. 四川師范大學(xué)學(xué)報(自然科學(xué)版),2015,38(6):802-809. [19] 李波,廖群英. 有限域上的k-型高斯正規(guī)基的對偶基及其乘法表[J]. 四川師范大學(xué)學(xué)報(自然科學(xué)版),2013,36(6):824-829. [20] 廖群英,胡曉蘭. 有限域上高斯正規(guī)基的一個注記[J]. 四川師范大學(xué)學(xué)報(自然科學(xué)版),2015,38(2):159-163. [21] 廖群英,李威,湯建剛. 有限域上一類自對偶正規(guī)基的乘法表與復(fù)雜度[J]. 四川師范大學(xué)學(xué)報(自然科學(xué)版),2014,37(1):31-36. 2010 MSC:12E20; 12E30; 11T99 (編輯 周 俊) The Primitive Properties for the Type (4,7) Gauss Normal Basisand Its Dual Basis over Finite Fields WEI Jie, LIAO Qunying, ZHOU Jiajun (Institute of Mathematics and Software Science, Sichuan Normal University, Chengdu 610066, Sichuan) Normal bases over finite fields are important in many efficient arithmetic implementations, such as coding theory and cryptography. In particular, primitive normal bases over finite fields have better properties and then are very important for applications. Recently, the explicit formula for the complexity of 7 type Gauss normal basesNofFq4overFqhas been obtained. The present paper continues to study the primitive properties forNand its dual basisB. Particularly, when the finite fieldFqhas characteristic 2 or 3, it proves thatNis a primitive normal basis if and only ifq=2 orq=3, in these case,Bis not primitive. finite field; Gauss normal basis; dual basis; primitive element 2015-09-22 國家自然科學(xué)基金(11401408)和四川省教育廳重點(diǎn)科研項(xiàng)目(14ZA0034) O156.1; O156.2 A 1001-8395(2016)06-0790-04 10.3969/j.issn.1001-8395.2016.06.002 *通信作者簡介:廖群英(1974—),女,教授,主要從事編碼與密碼學(xué)的研究,Email:qunyingliao@sicnu.edu.cn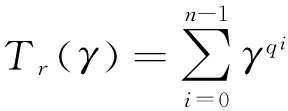
2 主要結(jié)果的證明