集值擬變分不等式的間隙函數和誤差界

楊 博, 夏福全

(四川師范大學 數學與軟件科學學院, 四川 成都 610066)

集值擬變分不等式的間隙函數和誤差界

楊 博, 夏福全*

(四川師范大學 數學與軟件科學學院, 四川 成都 610066)

首先研究集值擬變分不等式的間隙函數,然后利用該間隙函數建立集值擬變分不等式與優化問題間的等價關系,利用這一等價關系討論集值擬變分不等式的誤差界問題,這些結論是文獻(Fan H J, Wang G X. Comput Appl Math,2010,233:2956-2965和Tang G J, Huang N J. Taiwanese J Math,2013,17:1267-1286.)中相關結果的推廣.

集值擬變分不等式; 間隙函數; 誤差界

變分不等式在最優控制、非線性規劃、物理學、經濟學、工程學等諸多領域都有廣泛的應用,許多學者在變分不等式問題上作了深入研究,獲得了豐富結果[1-12].擬變分不等式問題出現相對較晚,但經過幾十年的發展,擬變分不等式的研究已較深入,并應用在力學及經濟學等問題中.

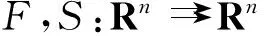
〈u*,y-x*〉≥0, ?y∈S(x*).

(1)

本文記集值映射S的不動點集、圖像、有效域分別為FP(S){x∈Rn|x∈S(x)}、Graph(S){(x,y)|x∈Dom(S),y∈S(x)}、Dom(S)={x∈X|S(x)≠?}.

如果F是一個單值映射,那么SQVI(F,S)退化為:求x*∈S(x*)滿足

〈F(x*),y-x*〉≥0, ?y∈S(x*).

(2)

對于單值擬變分不等式(2),文獻[13]首先定義了間隙函數f0(x):Rn→Rn∪{+∞}為

f0(x)=

-inf{〈F(x),y-x〉|y∈S(x)}.

(3)

在給定的條件下研究上述間隙函數f0(x)的連續性和可微性,同時也獲得關于間隙函數f0(x)的最優化問題與擬變分不等式(2)之間的等價性.文獻[14]定義單值擬變分不等式問題(2)的間隙函數fα(x):Rn→Rn為

fα(x)=max{-〈F(x),y-x〉-

αφ(x,y)|y∈S(x)}.

(4)

利用新定義的間隙函數,文獻[14]對文獻[13]的相關結果進行了推廣.

另一方面,若對任意的x∈Rn,S(x)≡S,其中S?Rn為非空子集,則SQVI(F,S)退化為求x*∈S,u*∈F(x*)滿足

〈u*,y-x*〉≥0, ?y∈S.

(5)

若F是一個單值映射,對任意的x∈Rn,S(x)≡S,其中S?Rn為非空子集,則SQVI(F,S)退化為下面的變分不等式問題:求x*∈S滿足

〈F(x*),y-x*〉≥0, ?y∈S.

(6)

文獻[15-16]定義(5)式的間隙函數fα(x):Rn→R為

fα(x)=

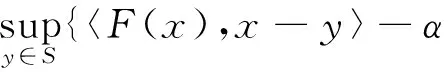
(7)

并獲得間隙函數的相關性質.

在此之后,文獻[11]利用(7)式定義問題(6)的新間隙函數

‖x-z‖}2,

證明關于φf(x,α,λ)的極小化問題與變分不等式問題(6)等價,并且研究φf(x,α,λ)的可微性,給出一些與誤差界相關的結果.

在(6)和(7)式的基礎上,文獻[1]定義了集值變分不等式問題(5)的間隙函數f:Rn×(0,+∞)→Rn為

f(x;α)=

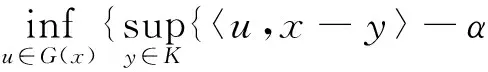
(8)

利用間隙函數(8),文獻[1]推廣了文獻[11]中相應的結論.除此之外,文獻[2]也將文獻[11]的變分不等式問題推廣為集值混合變分不等式,在給定的條件下,推廣文獻[11]中相應的結論.

受上述研究工作的啟發,本文研究了集值擬變分不等式間隙函數的性質以及與誤差界相關的結果,給出集值擬變分不等式新的間隙函數的定義,在給定的條件下,研究集值擬變分不等式間隙函數的相關性質以及與誤差界相關的結果,推廣了文獻[1-2]的相應結論.

1 預備知識

1) 強單調的,如果存在μ>0使得?x,y∈Rn,u∈F(x),v∈F(y)有

〈u-v,x-y〉≥μ‖x-y‖2;

2) 單調的,如果對?x,y∈Rn,u∈F(x),v∈F(y)有

〈u-v,y-x〉≥0;

3) 偽單調的,如果對?x,y∈Rn,u∈F(x),v∈F(y)有

〈u,y-x〉≥0?〈v,y-x〉≥0;

4) 關于x*強單調的,如果存在γ>0,對?x∈S(x*),u∈F(x)有

〈u,x-x*〉≥γ‖x-x*‖2,

其中x*是SQVI(F,S)的解.

注 1.1 若F是關于x*強單調的,則SQVI(F,S)的解x*是唯一的[17].此外,如果x*是SQVI(F,S)的解,F是強單調的,則F是關于x*強單調的,其中強單調系數γ∈(0,μ).事實上,因為x*是SQVI(F,S)的解,則存在u*∈F(x*)使得下列不等式成立

〈u*,x-x*〉≥0, ?x∈S(x*),

則對?x∈S(x*),u∈F(x)有

〈u,x-x*〉≥μ‖x-x*‖2+〈u*,x-x*〉

≥μ‖x-x*‖2≥γ‖x-x*‖2.

1)M(x)≥0,?x∈S(x);

2)M(x)=0,當且僅當x∈S(x)是問題(1)的解.

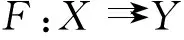
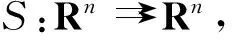
(y,x)?Graph(S),

則稱映射S具有不動點對稱性,顯然,這種性質可表示為

?x∈FP(S), ?y∈S(x)?x∈S(y).

下面的引理1.1參看文獻[18]的命題1.4.16.

).

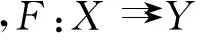
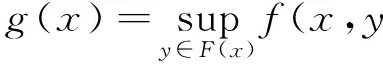
1) 若f和F是下半連續函數,則g(x)也是下半連續函數;

2) 若f是上半連續函數,F是上半連續函數并且是緊值的,則g(x)也是上半連續函數.

引理 1.2[19]令X是拓撲空間,φi:X→[-∞,+∞](i∈I)是下半連續函數,這里I是任意的指標集,則函數

下半連續.

2 間隙函數

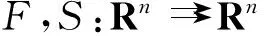
(9)

(10)

其中φ(x,y):Rn×Rn→R滿足下列條件:

(C1)φ在Rn×Rn上連續可微;

(C2)φ在Rn×Rn上非負且φ(x,y)=0,當且僅當x=y;

(C3)φ(x,·)關于x是一致強凸的,即存在常數μ>0,對?x∈Rn滿足

φ(x,y1)-φ(x,y2)≥〈yφ(x,y2),y1-y2〉+

μ‖y1-y2‖2, ?y1,y2∈Rn,

(C4)yφ(x,·)是Rn上具有模κ≥2μ的一致Lipschitz連續函數,也就是說,存在正數κ≥2μ使得對?x∈Rn有

‖y(x,y1)-y(x,y2)‖≤κ‖y1-y2‖,

?y1,y2∈Rn;

(C5) 對任意的x,y∈Rn,xφ(x,y)=-yφ(x,y).

注 2.1 易知,若φ(x,y)=‖x-y‖2,則φ(x,y)滿足(C1)～(C5).在這種情況下,(9)式退化為

‖x-y‖2}.

特別地,當S(x)=K,?x∈Rn,其中K?Rn為非空子集,則(9)式退化為參考文獻[1]中所定義的函數

‖x-y‖2}.

參看文獻[20]的引理2.1和引理4.2得引理2.1.

引理 2.1 令φ(x,y)滿足(C1)～(C5),則有:

2) 對所有的x,y∈S(x),

μ‖x-y‖2≤φ(x,y)≤(κ-μ)‖x-y‖2,

其中μ和κ分別為(C3)和(C4)中的常數.

首先研究本文所定義的函數(9)和(10)式所具有的一些性質.

1) 對任意的α>0和x∈S(x),有fα(x)≥0;

2) 對任意的α>0和x∈Rn,存在u0∈F(x),使得fα(x)=gα(x,u0);

3) 如果F上半連續,則對任意α>0,fα是下半連續函數.

證明 1) 若x∈S(x),則y=x∈S(x),有0∈{〈u,x-y〉-αφ(x,y)},故由gα(x,u)的定義得gα(x,y)≥0,因此

2) 因為〈u,x-y〉-αφ(x,y)關于u是連續的,且S是下半連續映射,由引理1.1的1)知gα(x,u)關于u是下半連續的.又因F是緊值的,故存在u0∈F(x)使得fα(x)=gα(x,u0).

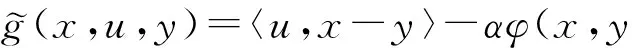
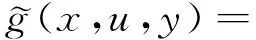
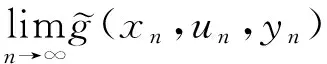
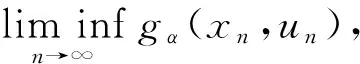
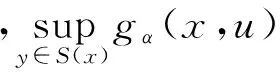
是下半連續函數.

證明 若fα(x*)=0,由fα(x)的定義,可得

因為S是下半連續的,由引理1.1的1)可知gα(x*,u)關于u是下半連續的,又因F(x*)是緊值的,則存在u*∈F(x*)使得

gα(x*,u*)=0.

因為〈u*,x*-y〉-αφ(x*,y)關于y是連續函數且S(x*)是緊值的,則由引理2.2,存在yα(x*)∈S(x*)滿足

gα(x*,u*)=〈u*,x*-yα(x*)〉-

αφ(x*,yα(x*))=0，

因此,

〈u*,yα(x*)-x*〉=

-αφ(x*,yα(x*))≤0.

(11)

因為yα(x*)∈S(x*)是

gα(x*,u*)=

的解,則由最優性條件得

〈u*+αyφ(x*,yα(x*)),y-yα(x*)〉≥0,

?y∈S(x*),

(12)

(12)式等價為

〈u*,yα(x*)-y〉≤

〈αyφ(x*,yα(x*)),y-yα(x*)〉,

?y∈S(x*).

因為x*∈FP(S),故x*∈S(x*).取x*=y,可得

〈u*,yα(x*)-x*〉≤

〈αyφ(x*,yα(x*)),x*-yα(x*)〉.

(13)

另一方面,由條件(C3)得

φ(x*,x*)-φ(x*,yα(x*))≥

μ‖x*-yα(x*)‖2,

由于φ(x*,x*)=0,由(13)式可得

〈αyφ(x*,yα(x*)),x*-yα(x*)〉≤

-αμ‖x*-yα(x*)‖2-

αφ(x*,yα(x*)).

(14)

結合(13)和(14)式得

〈u*,yα(x*)-x*〉≤

-αμ‖x*-yα(x*)‖2-αφ(x*,yα(x*)).

根據(11)式可得

αμ‖x*-yα(x*)‖2≤0.

故x*=yα(x*),x*是SQVI(F,S)的解.事實上,因為x*=yα(x*)結合(12)式,可得

〈u*+αyφ(x*,x*),y-x*〉≥0,

?y∈S(x*).

反之,如果x*是SQVI(F,S)的解,則x*∈S(x*)且存在u*∈F(x*)使得

〈u*,y-x*〉≥0, ?y∈S(x*),

則

gα(x*,u*)=

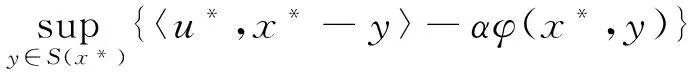
由此可得

gα(x*,u*)≤0.

對任意的x*∈S(x*),由引理2.2的1)可得:fα(x*)≥0,fα(x*)=0.

注 2.2 1) 如果對任意的x∈Rn,S(x)=S是一個非空的閉集,φ(x,y)=‖x-y‖2,則引理2.3退化成文獻[1]的引理3.3;

2) 如果F是一個單值映射,則引理2.3退化為文獻[14]的引理2.2.此外,如果φ(x,y)=0,則引理2.3等價為文獻[13]的定理2.

定義函數hβ:Rn→R∪{+∞}為

hβ(x)=

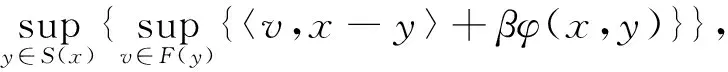
(15)

其中β≥0.顯然,如果x∈S(x),則hβ(x)≥0.

證明 1) 如果x*是SQVI(F,S)的解,則x*∈S(x*)且存在u*∈F(x*),使得

〈u*,y-x*〉≥0, ?y∈S(x*).

因為F是偽單調的,則有

〈v,y-x*〉≥0, ?y∈S(x*),v∈F(y),

可得

因為對?x*∈S(x*)和β≥0有hβ(x*)≥0,從而h0(x*)=0.

反之,如果h0(x*)=0,則有

〈v,x*-y〉≤0,

?y∈S(x*),v∈F(y).

本文斷言x*是SQVI(F,S)的解.若不然,因為x*∈S(x*),則存在y0∈S(x*),使得

〈u*,y0-x*〉<0, ?u*∈F(x*).

令A={u*∈Rn:〈u*,y0-x〉<0},則A是F(x*)的鄰域.因為x*,y0∈S(x*)且S(x*)是凸值的,則令xt=ty0+(1-t)x*∈S(x*),其中t∈(0,1].令t→0+,可得xt→x*,故存在x*的鄰域U,使得對充分小的t>0,xt∈U.因為A是F(x*)的鄰域,U是x*的鄰域,且xt∈U,由F是上半連續函數,可知F(xt)?A.由此可知,對每一個ut∈F(xt)有

〈ut,y0-x*〉<0.

對ut∈F(xt),xt∈S(x*),有下面的不等式

〈ut,xt-x*〉=t〈ut,y0-x*〉<0,

這與任意的y∈S(x*),v∈F(y)有〈v,y-x*〉≥0相矛盾.

2) 若β>0且hβ(x*)=0,由hβ(x*)的定義可得

〈v,x*-y〉+βφ(x*,y)≤0,

?y∈S(x*),v∈F(y).

因為φ(x*,y)≥0,則對所有y∈S(x*),v∈F(y),有〈v,x*-y〉≤0,后面的證明過程與引理2.4的1)的充分性證明相類似,由此可知x*是SQVI(F,S)的解.

反之,因為F關于SQVI(F,S)的解x*強單調的,故有

〈v,y-x*〉≥γ‖y-x*‖2,

?y∈S(x*),v∈F(y).

(16)

(16)式等價于

〈v,x*-y〉≤-γ‖y-x*‖2,

?y∈S(x*),v∈F(y).

由引理2.1的2)可得

〈v,x*-y〉+βφ(x*,y)≤

[β(κ-μ)-γ]‖x*-y‖2.

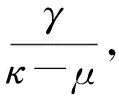
hβ(x*)=

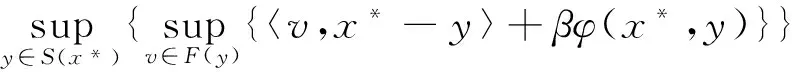
又因為對x*∈S(x*)都有hβ(x*)≥0,從而hβ(x*)=0.

考慮下面2個函數

(17)

和

(18)

其中,λ>0,fα(·)、hβ(·)分別定義為(10)和(15)式,因此(17)和(18)式可寫作

αφ(z,y)}}+λφ(x,z)}

(19)

和

βφ(z,y)}}+λφ(x,z)}.

(20)

下面將在不假設集值映射F可微的條件下,研究τf,α,λ(x)和τh,β,λ(x)的可微性.為了方便,對任意的α>0,β≥0,λ>0,分別定義ψf,α,λ(x,z):Rn×S(x)→(-∞,+∞]和ψh,β,λ(x,z):Rn×S(x)→(-∞,+∞]為

ψf,α,λ(x,z)=fα(z)+λφ(x,z),

ψh,β,λ(x,z)=hβ(z)+λφ(x,z).

因此,由(17)和(18)式所定義的τf,α,λ(x)、τh,β,λ(x)可改寫為

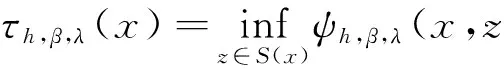
定理 2.1 若對任意α,λ>0及x∈Rn,函數ψf,α,λ(x,·)在S(x)上取得唯一的最小值zf,α,λ(x)且zf,α,λ(x)連續,則τf,α,λ(x)在Rn上可微且

證明 由τf,α,λ(·)、ψf,α,λ(·,·)、zf,α,λ(·)的定義,對每一個d∈Rn和ξ>0有

τf,α,λ(x+ξd)-τf,α,λ(x)≤

ψf,α,λ(x+ξd,zf,α,λ(x))-ψf,α,λ(x,zf,α,λ(x))=

λφ(x+ξd,zf,α,λ(x))-λφ(x,zf,α,λ(x)).

因此,在不等式的最左端和最右端同時除以ξ且讓ξ→0,可得

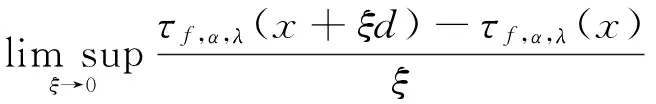
(21)

此外,對每一個d∈Rn和ξ>0,令xξ=x+ξd.由τf,α,λ(·)、ψf,α,λ(·,·)、zf,α,λ(·)的定義得

τf,α,λ(x+ξd)-τf,α,λ(x)=

τf,α,λ(xξ)-τf,α,λ(x)≥

ψf,α,λ(xξ,zf,α,λ(xξ))-

ψf,α,λ(x,zf,α,λ(xξ))=

λφ(x+ξd,zf,α,λ(x+ξd))-

λφ(x,zf,α,λ(x+ξd)).

因此,在不等式的最左端和最右端同時除以ξ且讓ξ→0,結合zf,α,λ(·)的連續性有

(22)

注意到(16)和(17)式對每一個d∈Rn有

λ〈xφ(x,zf,α,λ(x)),d〉,

定理 2.2 若對任意β≥0,λ>0及x∈Rn,函數ψh,β,λ(x,·)在S(x)上取得最小值zh,β,λ(x),且zh,β,λ(x)連續,則τh,β,λ(x)在Rn是可微的,且

證明 證明過程與定理2.1相類似.

3 誤差界

利用fα(·)、hβ(·)、τf,α,λ(·)、τh,β,λ(·)研究集值擬變分不等式問題(1)的誤差界.

fα(x)≥[γ-α(κ-μ)]‖x-x*‖2,

?x∈S(x*).

證明 因為F(x)是緊值的,且S是下半連續的,由引理2.2的2),對任何的x∈Rn,存在vx∈F(x),使得

fα(x)=gα(x,vx).

因為F是關于x*強單調的,則有

〈vx,x-x*〉≥γ‖x-x*‖2.

另一方面,因為S具有不動點對稱性,對任意的x∈S(x*),顯然有x*∈S(x).由引理2.1的2)可得

fα(x)=gα(x,vx)=

〈vx,x-x*〉-αφ(x,x*)≥

γ‖x-x*‖2-α(κ-μ)φ(x,x*)≥

[γ-α(κ-μ)]‖x-x*‖2.

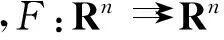
hβ(x)≥μβ‖x-x*‖2, ?x∈S(x*).

證明 因為x*是SQVI(F,S)的解,則x*∈S(x*)且存在u*∈F(x*)使得

〈u*,x-x*〉≥0, ?x∈S(x*).

因為S具有不動點對稱性,故對任意x∈S(x*)都有x*∈S(x).由引理2.1的2)可得

〈u*,x-x*〉+βφ(x,x*)≥

βφ(x,x*)≥μβ‖x-x*‖2.

‖x-x*‖2≤

τf,α,λ(x)≤λ(κ-μ)‖x-x*‖2,

?x∈S(x*).

證明 因為x*是SQVI(F,S)的解,則x*∈S(x*).由引理2.3有

fα(x*)=0.

對任意的x∈S(x*),因為S是不動點對稱的,則有x*∈S(x),結合引理2.1的2)可得

fα(x*)+λφ(x,x*)≤λφ(x,x*)≤

λ(κ-μ)‖x-x*‖2.

根據引理3.1可得

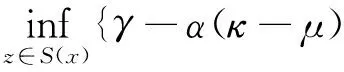
由不等式

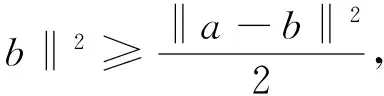
?a,b∈Rn,

則

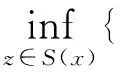
‖z-x*‖2+‖x-z‖2}≥

從而

τf,α,λ(x)≥

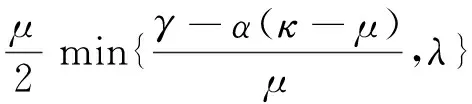
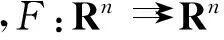
‖x-x*‖2≤

τh,β,λ(x)≤λ(κ-μ)‖x-x*‖2,

?x∈S(x*).

證明 對任意的x∈S(x*),因為S是不動點對稱的,則x*∈S(x).由x*是SQVI(F,S)的解,由引理2.4,可知hβ(x*)=0,右邊的不等式證明類似于定理3.1的證明.此外,結合引理3.2,左邊的不等式證明跟定理3.1最后一部分證明類似.

1) 若F、S是緊值的且S下半連續的,對任意的λ>0和x∈S(x*),則x*是SQVI(F,S)的解當且僅當τf,α,λ(x*)=0;

2) 若F是上半連續的且S是凸值的,對任意的λ>0和x∈S(x*),則x*是SQVI(F,S)的解當且僅當τh,β,λ(x*)=0.

證明 1) 如果x*是SQVI(F,S)的解,則x*∈S(x*).對任意x∈S(x*),讓x=x*,由定理3.1可得τf,α,λ(x*)=0.

反之,若τf,α,λ(x*)=0,由τf,α,λ(·)的定義可知,對任意的z∈S(x*)有

fα(z)+λφ(x*,z)≥0.

因為fα(z)+λφ(x,z)關于z是下半連續的且S是緊值的,則存在極小化序列{zn}∈S(x*)使得對任意的正整數n有

fα(zn)+λφ(x*,zn)≤

即存在序列{zn}∈S(x*),使得fα(zn)→0和φ(x*,zn)→0,則zn→x*.因為集合S(x*)是閉的,且zn∈S(x*),從而x*∈S(x*).由引理2.2可知fα(·)是下半連續和非負的,則有

0≤fα(x*)≤

因此,fα(x*)=0,從而,由引理2.3可知x*是SQVI(F,S)的解.

2) 如果x*是SQVI(F,S)的解,則x*∈S(x*).對任意的x∈S(x*),讓x=x*.又因為F是上半連續的且S是凸值的,由定理3.2可得τh,β,λ(x*)=0.反之,如果τh,β,λ(x*)=0,證明過程與定理3.3的1)的充分性證明相似.

[1] FAN H J, WANG G X. Gap functions and global error bounds for set-valued variational inequalities[J]. Comput Appl Math,2010,233(11):2956-2965.

[2] TANG G J, HUANG N J. Gap functions and global error bounds for set-valued mixed variational inequalities[J]. Taiwanese J Math,2013,17(4):1267-1286.

[3] HUAN L, JIANG B. Merit functions for general mixed qusi-variational inequalities[J]. J Appl Math Comput,2010,33(1):411-421.

[4] CHARITHA C, DUTTA J. Regularized gap functions and error bounds for vector variational inequalities[J]. Pac J Optim,2010,6(3):497-510.

[5] AUSSEL D, CORREA R, MARECHAL M. Gap functions for quasi-vatiational inequalities and generlized nash equilibrium problems[J]. J Optim Theory Appl,2011,151(151):474-488.

[6] AUSSEL D, GUPTA R, MARECHAL A. Gap functions and error bounds for quasi-vatiational inequality problems[J]. J Math Anal Appl,2013,407(2):270-280.

[7] SOLODOV M V, TSENG P. Some methods based on theD-gap function for solving monotone variational inequalities[J]. Comput Optim Appl,2000,17(2/3):255-277.

[8] HUANG L R, NG K F. Equivalent optimization formulations and error bounds for variational inequality problems[J]. J Optim Theory Appl,2005,125(2):299-314.

[9] HUANG N J, LI J, WU S Y. Gap functions for a system of generalized vector quasi-equilibrium problems with set-valued mappings[J]. J Global Optim,2008,41(3):401-415.

[10] FACCHINEI F, PANG J S. Finite-dimensional Vaeiational Inequalities and Complementary Problems[M]. New York:Spring-Verlag,2003.

[11] YAMASHIMA N, FUKUSHIMA M. Equivalent uncontrained minimization and global error bounds for variational inequality problems[J]. SIAM J Control Optim,1997,35(35):273-284.

[12] 夏福全,黎小波. Banach空間中分離變分不等式的 Levitin-Polyak-α適定性[J]. 四川師范大學學報(自然科學版),2012,35(3):430-434.

[13] FUKUSHIMA M. A class of gap functions for quasi-variational inequality problems[J]. J Ind Mang Optim,2007,3(2):165-171.

[14] TAJI K. On Gap functions for quasi-variational inequalities[J]. Abst Appl Anal,2008,2008:1563-1569..

[15] AUSLENDER A. Optimisation:Mecutethods Neumeriques[M]. Paris:Masson,1976.

[16] HEAM D W. The gap function of a convex program[J]. Oper Res Lett,1982,1(2):67-71.

[17] SOLODOV M.V. Merit functions and error bounds for generalized variational inequalities[J]. J Optim Theory Appl,2003,287(2):405-414.

[18] AUBIN J P, FRANKOWSKA H. Set-valued Analysis[M]. Boston:Birkhauser,1990.

[19] 福島雅夫. 非線性最優化基礎[M]. 北京:科學出版社,2011.

[20] YAMASHITA N, TAJI K, FUKUSHIMA M. Unconstrained optimization reformulations of variational inequality problems[J]. J Optim Theory Appl,1997,92(3):439-456.

2010 MSC：47H05; 47H04; 49J40; 49J30

(編輯 鄭月蓉)

Gap Functions and Error Bounds for Set-valued Quasi-variational Inequalities

YANG Bo, XIA Fuquan

(College of Mathematics and Software Science, Sichuan Normal University, Chengdu 610066, Sichuan)

In this paper, we consider the gap functions for set-valued quasi-variational inequalities. Using these gap functions, we show the equivalence between optimization problem and the set-valued quasi-variational inequalities. With the obtained equivalence results, we study error bounds for the solutions of set-valued quasi-variational inequalities(Fan H J, Wang G X. Comput Appl Math,2010,233:2956-2965, and Tang G J, Huang N J. Taiwanese J Math,2013,17:1267-1286.).

gap function; set-valued map; quasivariational inequality; error bound

2016-03-27

教育部科學技術重點項目(212147)

O176; O178

A

1001-8395(2016)06-0801-08

10.3969/j.issn.1001-8395.2016.06.004

*通信作者簡介：夏福全(1973—),男,教授,主要從事分拆理論與優化算法設計的研究,E-mail::fuquanxia@163.com