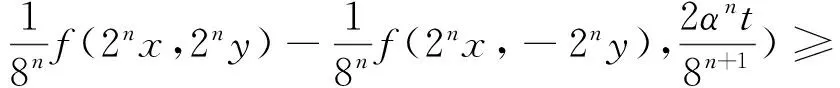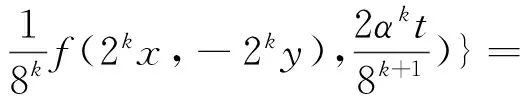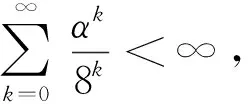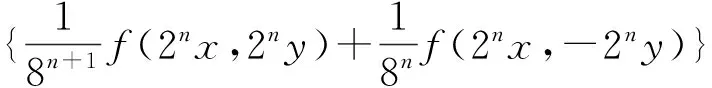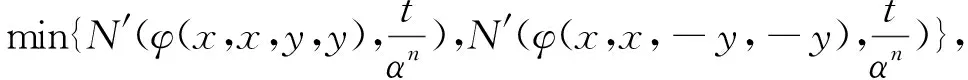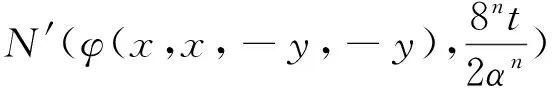Cauchy-Drygas型函數(shù)方程的Ulam穩(wěn)定性
宋愛民
(甘肅民族師范學院 數(shù)學系, 甘南 甘肅 747000)
Cauchy-Drygas型函數(shù)方程的Ulam穩(wěn)定性
宋愛民
(甘肅民族師范學院 數(shù)學系, 甘南 甘肅 747000)
給出Cauchy-Drygas型函數(shù)方程f(x1+x2,y1+y2)+f(x1+x2,y1-y2)=2f(x1,y1)+2f(x2,y1)+f(x1,y2)+f(x2,y2)+f(x1,-y2)+f(x2,-y2)的定義,并得到其一般解,同時,進一步討論Cauchy-Drygas型函數(shù)方程與混合二次-三次函數(shù)方程的關(guān)系,并在Banach空間及模糊賦范空間上討論它的Ulam穩(wěn)定性.
Cauchy-Drygas型函數(shù)方程; Banach空間; 模糊賦范空間; Ulam穩(wěn)定性
1 問題的提出
對于一個給定的算子T,及T的一個解集{μ}滿足T(μ)=0,考慮若存在ε>0滿足‖T(υ)‖≤ε,則是否存在μ及δ>0使得‖μ-υ‖≤δ(ε)成立.這一問題首先由S. M. Ulam[1]提出,所以也稱之為函數(shù)方程的Ulam穩(wěn)定性問題.D. H. Hyers[2]解決了Banach空間中近似Cauchy映射的Ulam穩(wěn)定性問題.Th. M. Rassias[3]將這種穩(wěn)定性推廣到廣義Hyers-Ulam-Rassias穩(wěn)定性.后來人們研究了各種映射的Ulam穩(wěn)定性如文獻[4-9].
始終設(shè)X和Y表示實向量空間.稱映射f:X→Y為Cauchy映射(或可加映射),若其滿足下列函數(shù)方程
f(x+y)=f(x)+f(y),
(1)
稱映射f:X→Y為Drygas映射,若其滿足函數(shù)方程
f(x+y)+f(x-y)=
2f(x)+f(y)+f(-y),
(2)
Drygas函數(shù)方程是H.Drygas[10]為了描述擬內(nèi)積空間而引入的函數(shù)方程,對于解決一些統(tǒng)計學上的問題起到過非常重要的作用.B. R. Ebanks[11]進一步等給出了Drygas函數(shù)方程的一般解.
引理 1.1 映射f:X→Y滿足Drygas函數(shù)方程當且僅當存在一個可加映射A:X→Y及一個對稱,雙可加的映射H:X2→Y,使得對任意的x∈X都有f(x)=H(x,x)+A(x).
證明 必要性 見文獻[11].
充分性 若f:X→Y滿足條件,則對?x,y∈X有
f(x+y)+f(x-y)-2f(x)-f(y)-f(-y)=
H(x+y,x+y)+H(x-y,x-y)-
2H(x,x)-H(y,y)-H(-y,-y)+
A(x+y)+A(x-y)-
2A(x)-A(y)-A(-y)=0,
從而充分性得證.事實上,
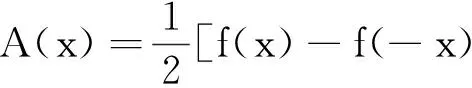
I.S.Chang等[12]給出了混合二次-三次方程
6f(x+y)-6f(x-y)+4f(3y)=
3f(x+2y)-3f(x-2y)+9f(2y)
(3)
在Banach空間的穩(wěn)定性并得到其一般解.
引理 1.2 映射f:X→Y滿足混合二次-三次函數(shù)方程當且僅當存在1個二元對稱,可加映射Q:X2→Y及1個三元對稱,可加的映射C:X3→Y,使得對任意的x∈X都有
f(x)=Q(x,x)+C(x,x,x).
事實上,此處
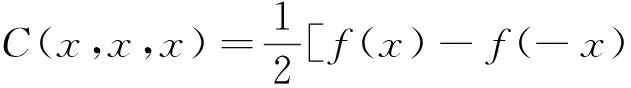
近年人們開始研究多元函數(shù)方程的穩(wěn)定性,如M.E.Gordji等[13]討論了三次-四次函數(shù)方程的Ulam穩(wěn)定性;N. Abbas等[14]討論了多元混合函數(shù)方程在Banach模上的穩(wěn)定性;Y. J. Cho等[15]討論了混合可加-三次-四次函數(shù)方程在隨機非阿基米德空間的穩(wěn)定性.
本文在上述研究的基礎(chǔ)上,定義了Cauchy-Drygas型函數(shù)方程,并得到了它的一般解及其與混合二次-三次函數(shù)方程的關(guān)系,最后討論了其在Banach空間以及模糊賦范空間上的Ulam穩(wěn)定性.
定義 1.3 映射f:X2→Y稱為Cauchy-Drygas型函數(shù)是指任給x1,x2,y1,y2∈X都滿足下列混合Cauchy-Drygas型函數(shù)方程:
f(x1+x2,y1+y2)+f(x1+x2,y1-y2)=
2f(x1,y1)+2f(x2,y1)+f(x1,y2)+
f(x2,y2)+f(x1,-y2)+f(x2,-y2).
(4)
2 函數(shù)方程(4)的一般解及其與(3)的關(guān)系
引理 2.1 映射f:X2→Y滿足方程(4)當且僅當f關(guān)于第一個變元是Cauchy的,關(guān)于第二個變元是Drygas的.即對任意的x1,x2,y1,y2都有
f(x1+x2,y)=f(x1,y)+f(x2,y),
f(x,y1+y2)+f(x,y1-y2)=
2f(x,y1)+f(x,y2)+f(x,-y2).
證明 充分性 顯然.下證必要性
必要性 設(shè)f:X2→Y滿足方程(4),在方程(4)中令x1=x2=y1=y2=0,顯然有f(0,0)=0;在方程(4)中令x2=y1=y2=0,顯然有f(x1,0)=0;在方程(4)中令y2=0,則有2f(x1+x2,y1)=2f(x1,y1)+2f(x2,y1),即f(x1+x2,y1)=f(x1,y1)+f(x2,y1),從而f關(guān)于第一個變元是Cauchy(可加)的.
在方程(4)中令x1=x2=y2=0,可得f(0,y1)=0;在方程(4)中令x2=0,則有f(x1,y1+y2)+f(x1,y1-y2)=2f(x1,y1)+f(x1,y2)+f(x1,-y2),從而f關(guān)于第二個變元是Drygas的.
定理 1.2 映射f:X2→Y滿足方程(4)當且僅當存在一個三元映射F:X3→Y及一個二元映射B:X2→Y,其中F關(guān)于第一個變量可加,關(guān)于后兩個變量對稱,可加;B關(guān)于2個變量分別可加,且滿足f(x,y)=F(x,y,y)+B(x,y).
證明 必要性 設(shè)f滿足方程(4),定義映射F:X3→Y,B:X2→Y,對?x1,y1,y2∈X令
F(x1,y1,y2)=
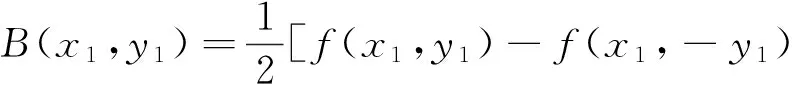
顯然,由f關(guān)于第一個變元是Cauchy的,固定y1,y2,則F關(guān)于第一個變量顯然是可加的;又由引理1.1中關(guān)于H的定義可知,F關(guān)于后兩個變量是對稱,可加的.類似的由f關(guān)于第一個變元是Cauchy的,固定y1,則B關(guān)于第一個變量顯然是可加的;由引理1.1中關(guān)于A的定義可知,B關(guān)于第二個變量是可加的,且
f(x,y)+f(x,y)-f(x,-y)]=
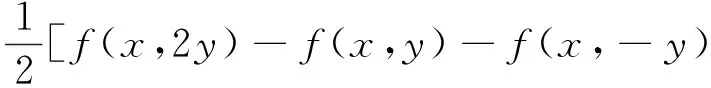
由于f關(guān)于第二個變元是Drygas的,從而f(x,2y)=2f(x,y)+f(x,y)+f(x,-y),也即F(x,y,y)+B(x,y)=f(x,y),必要性得證.
充分性 若存在滿足條件的映射F:X3→Y,B:X2→Y則由f(x,y)=F(x,y,y)+B(x,y),固定y,則F關(guān)于第一個變量可加,B關(guān)于第一個變量可加,從而f關(guān)于第一個變元是Cauchy的.固定x,則F關(guān)于后2個變量對稱,可加,B關(guān)于后一個變量可加,由引理1.1,f關(guān)于第二個變元是Drygas的,定理得證.
推論 2.3 設(shè)f:X2→Y是Cauchy-Drygas的,定義g:X→Y,g(x)=f(x,x),則g為混合二次-三次函數(shù).
證明 由定理2.2,存在一個三元映射F:X3→Y及一個二元映射B:X2→Y,其中F關(guān)于第一個變量可加,關(guān)于后2個變量對稱,可加;B關(guān)于第一個變量可加,關(guān)于第二個變量可加,且滿足
f(x,y)=F(x,y,y)+B(x,y).
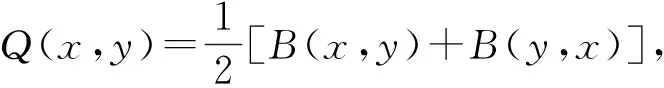
不難看出,Q(x,x)=B(x,x),C(x,x,x)=F(x,x,x),從而g(x)=f(x,x)=B(x,x)+F(x,x,x)=Q(x,x)+C(x,x,x).顯然g滿足引理1.2的條件,從而g為混合二次-三次函數(shù).
推論 2.4 設(shè)映射g:X→Y為混合二次-三次函數(shù),定義映射f:X2→Y滿足
2[g(2y-x)+g(-2y+x)]+
2[g(2x+y)+g(-2x-y)]+
2[g(2x-y)+g(-2x+y)]-
5[g(x+y)+g(-x-y)]-
g(-2y-x)]-[g(2y-x)-g(-2y+x)]-
[g(x+y)-g(-x-y)]+
[g(y-x)-g(-y+x)]}.
則f為Drygas-二次函數(shù),且有g(shù)(x)=f(x,x).
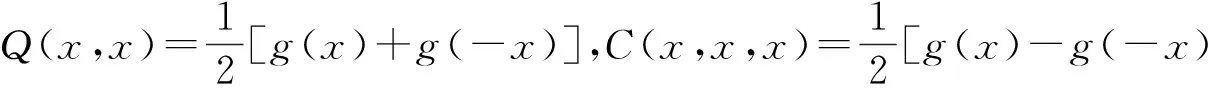
Q(2y+x,2y+x)+Q(2y-x,2y-x)=
Q(x,x)+4Q(y,y)+4Q(x,y),
從而顯然有
Q(2x+y,2x+y)+Q(2x-y,2x-y)=
4Q(x,x)+Q(y,y)+4Q(x,y),
又
Q(y+x,y+x)+Q(y-x,y-x)=
2Q(y,y)+2Q(x,x).
綜合上面3式有
2[g(2y-x)+g(-2y+x)]+
2[g(2x+y)+g(-2x-y)]+
2[g(2x-y)+g(-2x+y)]-
5[g(x+y)+g(-x-y)]-
5[g(y-x)+g(-y+x)]}
又因為
C(2y+x,2y+x,2y+x)-
C(2y-x,2y-x,2y-x)=
24C(x,y,y)+2C(x,x,y);
C(y+x,y+x,y+x)-C(y-x,y-x,y-x)=
6C(x,y,y)+2C(x,x,y).
綜合上面2式有
[g(2y-x)-g(-2y+x)]-
[g(x+y)-g(-x-y)]+
[g(y-x)-g(-y+x)]}.
從而
2[g(2y-x)+g(-2y+x)]+
2[g(2x+y)+g(-2x-y)]+
2[g(2x-y)+g(-2x+y)]-
5[g(x+y)+g(-x-y)]-
g(-2y-x)]-[g(2y-x)-g(-2y+x)]-
[g(x+y)-g(-x-y)]+
[g(y-x)-g(-y+x)]}=
Q(x,y)+C(x,y,y).
進而由定理2.2可知,f為Cauchy-Drygas的,顯然有g(shù)(x)=f(x,x),定理得證.
在下面的證明過程中,對于映射f:X2→Y,算子Df:X4→Y,記
Df(x1,x2,y1,y2)=f(x1+x2,y1+y2)+
f(x1+x2,y1-y2)-2f(x1,y1)-2f(x2,y1)-
f(x1,y2)-f(x2,y2)-
f(x1,-y2)-f(x2,-y2),
顯然f是Cauchy-Drygas的當且僅當?x1,x2,y1,y2∈X,Df(x1,x2,y1,y2)=0.3 函數(shù)方程(4)在Banach空間上的Ulam穩(wěn)定性
本節(jié)始終設(shè)X是實的向量空間,Y是Banach空間.
定理 3.1 給定函數(shù)φ:X4→[0,+∞)滿足對任意的x1,x2,y1,y2∈X都有
Φ(x1,x2,y1,y2)=
φ(2nx1,2nx2,-2ny1,-2ny2)]<∞.
(5)
如果映射f:X2→Y滿足對任意x1,x2,y1,y2∈X都有
‖Df(x1,x2,y1,y2)‖≤φ(x1,x2,y1,y2),
(6)
且當x=0或y=0時有f(x,y)=0,則存在滿足函數(shù)方程(4)的Cauchy-Drygas型函數(shù)C:X2→Y,使得對任意x,y∈X有
‖C(x,y)-f(x,y)-f(x,-y)‖≤
Φ(x,x,y,y).
(7)
證明 由(6)式顯然可得
‖Df(x1,x2,y1,y2)+Df(x1,x2,-y1,-y2)‖≤
φ(x1,x2,y1,y2)+φ(x1,x2,-y1,-y2).
(8)
在(8)式中,令x1=x2=x,y1=y2=y,有
‖f(2x,2y)+f(2x,-2y)-
8f(x,y)-8f(x,-y)‖≤
φ(x,x,y,y)+φ(x,x,-y,-y),
在上式中用2nx代替x,2ny代替y,且兩邊同除以8n+1,則有
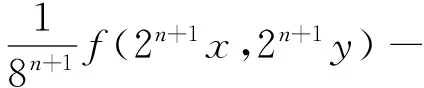
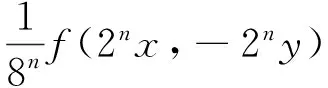
φ(2nx,2nx,-2ny,-2ny),
(9)
從而對任給正整數(shù)m φ(2ix,2ix,-2iy,-2iy)], 在(6)式中用2nxi代替xi,用2nyi代替yi,則有 ‖DC(x1,x2,y1,y2)‖= Df(2nx1,2nx2,-2ny1,-2ny2)‖≤ φ(2nx1,2nx2,-2ny1,-2ny2)]=0, 從而可得DC(x1,x2,y1,y2)=0,也就是說C是Cauchy-Drygas的. 在(9)式中令m=0,n→∞,則有 ‖C(x,y)-f(x,y)-f(x,-y)‖≤Φ(x,x,y,y), (7)式得證. 本節(jié)始終設(shè)X為線性空間,Y是一個模糊Banach空間. 定理 4.1 設(shè)(Z,N′)為模糊賦范空間,映射φ:X4→Z滿足存在實數(shù)α,其中0<|α|<8,使得對?x1,x2,y1,y2∈X,t>0都有 φ(2x1,2x2,2y1,2y2)= αφ(x1,x2,y1,y2), (10) 映射f:X2→Y滿足對任意的x1,x2,y1,y2∈X,t>0都有 N(Df(x1,x2,y1,y2),t)≥ N′(φ(x1,x2,y1,y2),t), (11) 且當x=0或y=0時有f(x,y)=0,則存在Cauchy-Drygas型函數(shù)C:X2→Y,使得對任意x,y∈X有 N(C(x,y)-f(x,y)-f(x,-y),t)≥ (12) 其中M((x,y),t)=min{N′(φ(x,x,y,y),t),N′(φ(x,x,-y,-y),t)}. 證明 不失一般性,此處設(shè)0<α<8,由(11)式,顯然可得 N(Df(x1,x2,y1,y2)+Df(x1,x2,-y1,-y2),2t)≥ min{N′(φ(x1,x2,y1,y2),t), N′(φ(x1,x2,-y1,-y2),t)}. (13) 在(13)式中令x1=x2=x,y1=y2=y,從而 N(Df(x,x,y,y)+Df(x,x,-y,-y),2t)≥ min{N′(φ(x,x,y,y),t),N′(φ(x,x,-y,-y),t)}, 也即 N(f(2x,2y)+f(2x,-2y)- 8f(x,y)-8f(x,-y),2t)≥min{N′(φ(x,x,y,y),t),N′(φ(x,x,-y,-y),t)}. 在上式中,用2nx代替x,2ny代替y,則有 min{N′(φ(2nx,2nx,2ny,2ny),t), N′(φ(2nx,2nx,-2ny,-2ny),t)}= min{N′(αnφ(x,x,y,y),t), 進一步有 從而對任給正整數(shù)m 從而有 (14) 在(13)式中用2nxi代替xi,用2nyi代替yi,這里i=1,2,則有 min{N′(φ(2nx1,2nx2,2ny1,2ny2),t), 從而 DC(x1,x2,y1,y2)=0, 即C為Cauchy-Drygas的.在(14)式中令m=0,n→∞,可得 N(C(x,y)-f(x,y)-f(x,-y),t)≥ 從而定理得證. [1] ULAM S M. Problem in Modern Mathematics[M]. New York:John Wiley & Sons,1940. [2] HYERS D H. On the stability of the linear functional equation [J] . Proc Am Math Soc,1941,72(2):222-224. [3] RASSIAS Th M. On the stability of the linear mapping in Banach spaces [J]. Proc Am Math Soc,1978,72(2):297-300. [4] ESKANDANI G Z, GRUTAL P, RASSIAS J M, et al. Generalized Hyers-Ulam stability for a general mixed functional equation in quasi-β-normed spaces[J]. Mediterranean J Math,2011,8(3):331-348. [5] NAJATI A, RANJBARI A. Stability of homomorphisms for a 3D Cauchy-Jensen type functional equation on C-ternary algebras[J]. J Math Analysis Appl,2008,341(1):62-79. [6] POPA D. Hyers-Ulam-Rassias stability of a linear recurrence[J]. J Math Anal Appl,2005,309(2):591-597. [7] 玉強. 郭艷平. 一般四次方程的穩(wěn)定性[J]. 四川師范大學學報(自然科學版),2013,36(5):703-707. [8] 宋愛民. 混合Cauchy-四次函數(shù)方程的Ulam穩(wěn)定性[J]. 重慶師范大學學報(自然科學版),2016,33(5):50-58. [9] 柴志成, 秦曉波. Shannon-Khinchin公理的Ulam穩(wěn)定性[J]. 四川師范大學學報(自然科學版),2014,37(3):348-353. [10] DRYGAS H. Quasi-inner products and their applications[C]//Advances in Multivariate Statistical Analysis. Berlin:Springer-Verlag,1987:13-30. [11] EBANKS B R, KANNAPPAN P, SAHOO P K, et al. A common generalization of functional equations characterizing normed and quasi-inner-product spaces[J]. Canadian Mathematical Bulletin,1992,35(3):321-327. [12] CHANG I S, JUNG Y S. Stability of a functional equation deriving from cubic and quadratic functions[J]. J Math Anal Appl,2003,283(2):491-500. [13] GORDJI M E, EBADIAN A, ZOLFAGHRI S. Stability of a functional equation deriving from cubic and quartic functions[J]. Abs Appl Anal,2008,2008(1):1563-1569. [14] ABBAS N, RASSIAS Th M, Stability of a mixed functional equation in several variables on Banach modules[J]. Nonlinear Analysis,2010,72:1755-1767. [15] CHO Y J, SAADATI R. Lattictic non-archimedean random stability of ACQ functional equation[J]. Adv Diff Eqns,2011,2011(1):348-357. 2010 MSC:39B72; 47H15 (編輯 陶志寧) The Ulam Stability Of Cauchy-Drygas Functional Equation SONG Aimin (College of mathematics, Gansu normal University for nationalities, Gannan 747000, Gansu ) In this paper, we define the Cauchy- Drygas functional equationf(x1+x2,y1+y2)+f(x1+x2,y1-y2)=2f(x1,y1)+2f(x2,y1)+f(x1,y2)+f(x2,y2)+f(x1,-y2)+f(x2,-y2), and obtain its general solution. Moreover, we establish the relationship between Cauchy-Drygas functional equation and quadratic-cubic functional equation, and prove the Ulam stability of Cauchy-Drygas functional equation in Banach space and fuzzy normed space. Cauchy-Drygas functional equation; Banach space; fuzzy, respectively normed space; Ulam stability 2015-12-22 甘肅省高等學校科研項目(2015B-120) 宋愛民(1984—),男,籍貫甘肅蘭州,講師,主要從事算子代數(shù)及其應用方面的研究,E-mail:songaimin@yahoo.com O177.1 A 1001-8395(2016)06-0851-06 10.3969/j.issn.1001-8395.2016.06.014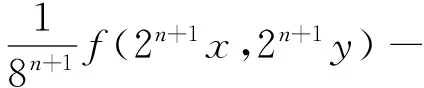
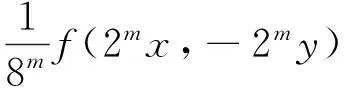
4 方程(4)在模糊賦范空間的Ulam穩(wěn)定性