具有復(fù)階的近于凸函數(shù)子族的系數(shù)估計

范臣君, 秦 川, 李小飛

( 1. 長江大學(xué) 工程技術(shù)學(xué)院, 湖北 荊州 434020; 2. 長江大學(xué) 信息與數(shù)學(xué)學(xué)院, 湖北 荊州 434000; 3. 澳門大學(xué) 數(shù)學(xué)系, 中國 澳門 999078)

具有復(fù)階的近于凸函數(shù)子族的系數(shù)估計

范臣君1, 秦 川1, 李小飛2,3

( 1. 長江大學(xué) 工程技術(shù)學(xué)院, 湖北 荊州 434020; 2. 長江大學(xué) 信息與數(shù)學(xué)學(xué)院, 湖北 荊州 434000; 3. 澳門大學(xué) 數(shù)學(xué)系, 中國 澳門 999078)

復(fù)階; 近于凸函數(shù); 從屬; Salagean算子

1 預(yù)備知識

本文用C表示復(fù)數(shù)集,C0=C{0}表示非零復(fù)數(shù)集,N表示正整數(shù)集,N0表示非負整數(shù)集,N*=N{1}.記A表示單位圓盤U={z∈C:|z|<1}內(nèi)形如下式的解析函數(shù)族

(1)

設(shè)f(z)和g(z)在U內(nèi)解析,稱f(z)從屬于g(z),記作f(z)g(z),若存在U內(nèi)的Schwarz函數(shù)ω滿足ω(0)=0,|ω(z)|<1,使得f(z)=g(ω(z)).特別地,若g在U內(nèi)單葉,上述從屬關(guān)系等價于f(0)=g(0),f(U)?g(U).用S*(γ)、C(γ)、K(γ)、Q(γ)分別表示A中的γ階(γ∈C0)的星象函數(shù)族、凸函數(shù)族、近于凸函數(shù)族、擬凸函數(shù)族(見文獻[1-8]).對于f(z)∈A,G. S. Salagean[9]定義了一類Salagean微分算子Dn(n∈N)如下

D0f(z)=f(z),D1f(z)=Df(z)=zf′(z),…,

Dnf(z)=D(Dn-1)f(z).

經(jīng)計算

記h:U→C為正規(guī)的正實部凸函數(shù)族,即h(0)=1,Re{h(z)}>0.H. M. Srivastava等[10]引入了一類γ階解析函數(shù)類S(λ,γ,A,B)定義如下

S(λ,γ,A,B)={f(z):f(z)∈A,

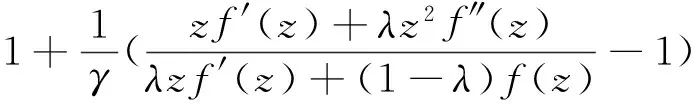
并對函數(shù)類S(λ,γ,A,B)的系數(shù)進行了估計.Q. H. Xu等[11]在函數(shù)類S(λ,γ,A,B)的基礎(chǔ)上定義了函數(shù)類Sh(λ,γ)如下

Sh(λ,γ)={f(z):f(z)∈A,

h(U),0≤λ≤1,γ∈C0}.

h(U),0≤λ≤1,γ∈C0}.

最近,C. Selvaraj等[13]利用Salagean算子定義了函數(shù)類CV(n,γ,g)如下

CV(n,γ,h)={f(z):f(z)∈A,

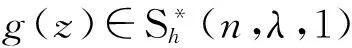
h(U), 0≤λ≤1,γ∈C0.

注意到,若取h(z)=(1+z)/(1-z),那么

KQh(0,0,γ)=K(γ), KQh(0,1,γ)=Q(γ).

h(U), 0≤λ≤1,γ∈C0.

h(U), 0≤λ≤1,γ∈C0.

定義 1.3 稱f(z)∈Mh(n,λ,γ;μ),若f(z)滿足下面的Cauchy-Euler型非齊次微分方程[19-22]

(1+μ)(2+μ)h(z),

(2)

其中,w=f(z),h(z)∈TQh(n,λ,γ),μ∈R(-∞,-1].

2 主要結(jié)論

為了得到本文的結(jié)論,需要用到下面引理.

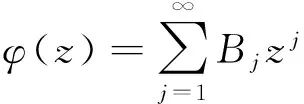
|Cj|≤|B1|,j∈N.

F(z)=[(1-λ)Dnf(z)+λDn+1f(z)]′,

則有

經(jīng)簡單計算得到

其中

Aj=(1+(j-1)λ)jn+1aj,j∈N*.

現(xiàn)記

(3)

經(jīng)計算,p(0)=h(0)=1,且p(z)∈h(U),因此p(z)h(z).由引理2.1知

(4)

將(3)式變形得

zF′(z)=γF(z)(p(z)-1).

(5)

現(xiàn)設(shè)p(z)=1+p1z+p2z2+…,z∈U,其中,pm=p(m)(0)/m!,m∈N.因為A1=1,由(5)式知

比較兩邊zj-1的系數(shù)得

(j-1)Aj=

γ(p1Aj-1+p2Aj-1+…+pj-1A1),

(6)

聯(lián)合(4)和(6)兩式,取j=2,3,4,得

|A2|≤|h′(0)||γ|,

|A3|≤|h′(0)||γ|(1+|h′(0)||γ|)/2!,

|A4|≤|h′(0)||γ|(1+|h′(0)||γ|)×

(2+|h′(0)||γ|)/3!,

應(yīng)用數(shù)學(xué)歸納法容易得到

因此

定理 2.3 若由(1)式表示的函數(shù)f(z)∈TQh(n,λ,γ),則有

F(z)=[(1-λ)Dnf(z)+λDn+1f(z)]′=

G(z)=[(1-λ)Dng(z)+λDn+1g(z)]′=

其中

Aj=(1+(j-1)λ)jn+1aj,

Bj=(1+(j-1)λ)jn+1bj,

則由定義知

令

即

zF′(z)=γG(z)(p(z)-1).

(7)

設(shè)p(z)=1+p1z+p2z2+…,z∈U,因為B1=1,由(7)式知

比較兩邊zj-1的系數(shù)得

即

因此

定理 2.4 若由(1)式表示的函數(shù)f(z)∈Mh(n,λ,γ;μ),則有

|aj|≤

證明 由于f(z)∈Mh(n,λ,γ;μ),則存在

滿足(2)式,對(2)式兩邊變形得

(8)

由(8)式和定理2.4得

|aj|≤

致謝 長江大學(xué)工程技術(shù)學(xué)院科技創(chuàng)新基金(15J0802)對本文給予了資助,謹(jǐn)致謝意.

[1] KOWN O S, OWA S. On quasi convex functions of complex order[J]. Soochow J Math,1994,20:241-250.

[2] NASR M A, AOUF M K. Radius of convexity for the class of starlike functions of complex order[J]. Bull Fac Sci Assiut Univ,1983,A12(1):153-159.

[3] NOOR K I. Quasi-convex functions of complex order[J]. Pan Am Math J,1993,3(2):81-90.

[4] OWA S, NUNOKAWA M, SAITON H, et al. Close-to-convexity, starlikeness, and convexity of certain analytic functions[J]. Appl Math Lett,2002,15(1):63-69.

[5] 牛瀟萌,李書海,湯獲. 近于凸函數(shù)的新子類[J]. 西南民族大學(xué)學(xué)報(自然科學(xué)版),2016,42(3):318-323.

[6] 秦川,馮建中,李小飛. Pascu類亞純雙單葉函數(shù)的系數(shù)估計[J]. 四川師范大學(xué)學(xué)報(自然科學(xué)版),2016,39(3):349-353.

[7] 秦川,李小飛. 一類利用復(fù)合算子函數(shù)定義的解析函數(shù)類的包含性質(zhì)[J]. 四川師范大學(xué)學(xué)報(自然科學(xué)版),2016,38(3):376-380.

[8] 熊良鵬. 雙單葉星形和凸函數(shù)的系數(shù)邊界[J]. 西南大學(xué)學(xué)報(自然科學(xué)版),2015,40(6):5-9.

[9] SALAGEAN G S. Complex Analysis[M]. New York:Springer-Verlag,1983:362-372.

[10] SRIVASTAVA H M, AITNTAS O, SERENBAY K S. Coefficient bounds for certain subclasses of starlike functions of complex order[J]. Appl Math Lett,2011,24(8):1359-1363.

[11] XU Q H, GUI Y C, SRIVASTAVA H M. Coefficient estimates for certain subclasses of analysis functions of complex order[J]. Taiwanese J Math,2011,15(5):2377-2386.

[12] SRIVASTAVA H M, XU Q H, WU G P. Coefficient estimates for certain subclasses of spiral-like functions of complex order[J]. Appl Math Lett,2010,23(7):763-768.

[13] SELVARAJ C, THIRUPATHI G. Coefficient bounds for a subclass of bi-univalent functions using Salagean operator[J]. Acta Universitatis Apulensis,2014,39:215-223.

[14] 都俊杰,鄒發(fā)偉,秦川,等. 一類利用從屬關(guān)系定義的復(fù)數(shù)階雙單葉函數(shù)類的系數(shù)問題[J]. 四川師范大學(xué)學(xué)報(自然科學(xué)版),2015,39(3):344-348.

[15] 鄧琴. 具有復(fù)階的解析函數(shù)族[J]. 數(shù)學(xué)物理學(xué)報,2011,A31(4):1045-1054.

[16] 熬恩,李書海,張國偉. 關(guān)于一類復(fù)階星象函數(shù)的Fekete-Szego不等式[J]. 數(shù)學(xué)的實踐與認(rèn)識,2015,45(1):249-255.

[17] 劉鶴,于濤. 一類復(fù)階單葉函數(shù)的系數(shù)估計[J]. 陰山學(xué)刊,2010,24(1):14-15.

[18] UI-HAQ W, MANZAR S. Coefficient estimates for certain subfamilies of close-to-convex of complex order[J]. Filomat,2016,30(1):99-103.

[19] ALTINATAS O, OZKAN O, SRIVASTAVA H M. Neighbourhoods of a class of analytic functions with negative coefficients[J]. Appl Math Lett,2000,13(3):63-67.

[20] CAGLAR M, ORHAN H, YAGMUR N. Coefficient bounds for new subclasses of bi-univalent functions[J]. Filomat,2013,27(7):1165-1171.

[21] JAHANGIRI J M, KIM Y C, SRIVASTAVA H M. Construction of a certain class of harmonic close-to-convex functions associated with the Alexander integral transform[J]. Integral Transforms Spec Funct,2003,14(3):237-242.

[22] UI-HAQ W, NAZNEEN A, ARIF M, et al. Coefficient bounds for certain subclasses of close-to-convex functions of Janowski type[J]. J Comput Anal Appl,2014,16(1):133-138.

[23] ROGOSINSKI W. On the coefficients of subordinate functions[J]. Proc London Math Soc,1945,2(1):48-82.

2010 MSC：30C45

(編輯 李德華)

Coefficient Estimates for Subclasses of Close-to-convex Functions with Complex Order

FAN Chenjun1, QIN Chuan1, LI Xiaofei2,3

( 1. College of Engineering and Technology, Yangtze University, Jingzhou 434020, Hubei; 2. Faculy of Information and Mathematics, Yangtze University, Jingzhou 434000, Hubei; 3. Department of Mathematics, University of Macau, Macau 999078, China

complex order; close-to-convex; subordinary; Salagean operater

2016-07-15

國家自然科學(xué)基金(61503047)和湖北省自然科學(xué)基金(2013CFAO053)

范臣君(1984—),男,講師,主要從事泛函分析與最優(yōu)化理論的研究,E-mail:fcjun0222@163.com

O174.51

A

1001-8395(2016)06-0865-04

10.3969/j.issn.1001-8395.2016.06.017