基于黃金分割率模型的鋼筋混凝土梁橋裂縫模式研究

宋 軍，周建庭，王明斌，姜 睿

(1.魯東大學 土木工程學院，山東 煙臺 264025；2.重慶交通大學 土木工程學院，重慶 400074)

基于黃金分割率模型的鋼筋混凝土梁橋裂縫模式研究

宋 軍1，周建庭2，王明斌1，姜 睿1

(1.魯東大學 土木工程學院，山東 煙臺 264025；2.重慶交通大學 土木工程學院，重慶 400074)

從新的視角出發，引入黃金分割率來評價鋼筋混凝土梁橋的裂縫分布模式。基于混凝土“單筋張拉模型”并編寫程序來預測混凝土開裂后裂縫寬度和間距，結合模型實驗和數值模擬驗證了參數的準確性。研究結果表明：采用黃金分割率來剖析鋼筋混凝土梁的裂縫分布具有深刻的物理意義，研究結果也揭示了混凝土梁裂縫間距具有尺寸效應，該方法的重要意義在于可以通過縮尺模型來預測大型橋梁的裂縫分布模式，對于評價混凝土梁橋的安全性有指導作用。

橋梁工程；裂縫模式；黃金分割率；尺寸效應

0 引 言

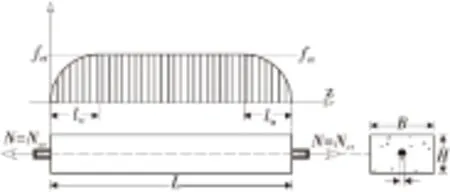
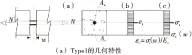
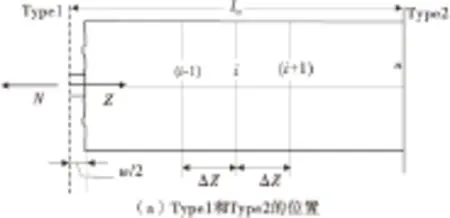
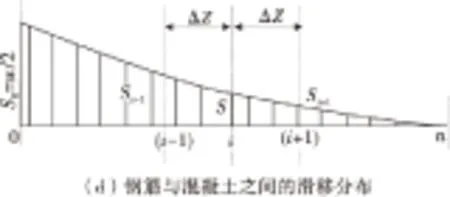
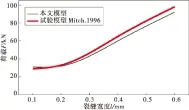
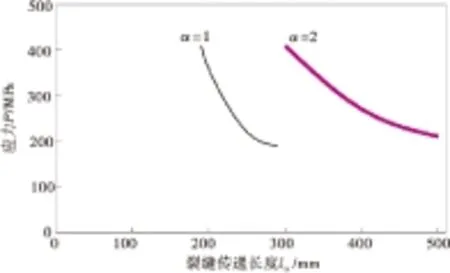
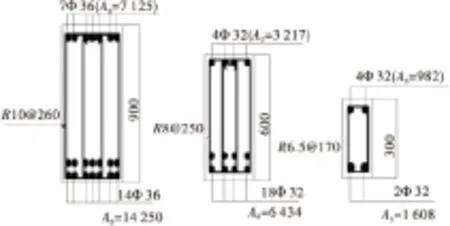
經典的鋼筋混凝土開裂理論是建立在基于傳遞長度的評價方法上，混凝土中的最大拉應力出現的截面最有可能出現新的裂縫，在鋼筋混凝土梁中這個裂縫間距用lSr表示，它的范圍是ltr

A.P.FANTILLI等[1]建立了鋼筋和混凝土之間的黏結滑移模型。它們之間的相互作用影響因素主要是通過參數實驗(強度和摩擦力等)得到，但是沒有充分考慮學者A.CARPINTERI[7]的建議模型以及并沒有考慮試件的尺寸效應的影響。

陳輝[3]對歐幾里德最早提出的“黃金分割”這一概念進行了詳細闡述。將一條線段進行分割，當C與B的比值等于B與A的比值且等于0.618時，這一分割點就稱為黃金分割點，如圖1。

圖1 黃金分割點的劃分Fig.1 Division of golden section

(1)

計算黃金分割最簡單方法，是計算斐波那契數列(1, 2, 3, 5, 8, 13, 21,…)，后二數之比2/3,3/5,5/8,8/13,13/21, …。即相鄰兩個斐波那契數的比值是隨序號的增加而逐漸逼近黃金分割比。

黃金分割率雖然被應用在多個學科領域，但是基本都是應用其幾何屬性，缺乏結構力學問題的深度剖析[8-9]。C.M.MOORMAN等[10]利用黃金分割率分析了經典的耦合振蕩問題；YI Zhijian等[11]應用黃金比例裂紋板的彈塑性問題。由此可見，黃金分割率在這些研究中起到了關鍵作用。

筆者應用黃金分割率分析了混凝土梁的裂縫分布模式。應用“單筋張拉模型”建立平衡方程；并采用數值手段編程預測裂縫寬度和裂縫間距；通過室內模型實驗和數值模擬相互驗證了鋼筋混凝土梁開裂的裂縫間距具有尺寸效應的存在。

1 裂縫計算模型

為計算鋼筋混凝土梁的裂縫模式，現以一個合理的單筋梁拉伸模型為例(圖2)，通過分析單梁的裂縫分布結果來反演其他橋梁結構裂縫分布規律。

圖2 單根鋼筋在水平拉力作用下的應力分布Fig.2 Tensile stresses in the concrete that surround a steel reinforcing bar in tension

圖2中的鋼筋混凝土梁的拉伸實驗模型可以用于揭示開裂現象。當法向荷載達到開裂荷載后，裂縫會出現在(L-2ltr)位置(L為鋼筋混凝土梁長度，ltr為裂縫傳遞長度)，此時混凝土拉應力達到規范容許的抗拉強度值即fct。

裂縫的開展具有一定隨機性，筆者考慮了兩種工況下的應力應變計算結果。其中：Type1表示初始狀態已經存在初始裂縫(寬度為w)情況〔圖3(a)〕；Type2表示未產生裂縫情況〔圖3(b)〕。現討論該兩種工況下梁的裂縫模式，如果給定一個軸向力N，以及鋼筋的應變εs和混凝土的應變εc，則可得到式(2)：

N=σsAs+σcAc=EsεsAs+EcεcAc

(2)

式中：As和Ac分別為鋼筋和混凝土的面積；Es和Ec分別為鋼筋和混凝土的彈性模量；σs和σc分別為鋼筋和混凝土的應力。

圖3 兩種工況下的幾何特性Fig.3 Geometric characteristics under two conditions

由式(2)可以獲得鋼筋應變和混凝土應變。

考慮到最大裂縫寬度的鋼筋混凝土梁中，假設加載過程符合平截面假定，那么在荷載作用下最大裂縫間距將會發生變化。這一變化規律即為約等于新裂紋一半的間距，新裂紋早期形成的圖式如上圖。在這種情形下，新裂紋產生的斷面將會是混凝土應力達到極限張拉應力之后。

2 程序計算

由圖3提出Type1和Type2兩種類型，構建如圖4的計算簡圖。其中：Type1截面中，Z=0時，s(Z=0)=w/2,；Type2截面中，Z=ltr時，σc(Z=ltr)=fct。

圖4 計算簡圖Fig.4 Computing model

編寫計算程序如下：

1)假設一個裂縫寬度數值(圖4)；

2)假設張拉鋼筋的一個實驗荷載值；

3)計算Type1型截面的法向應力；

4)從Type2型截面的計算模式中可以獲取初始裂縫出現時候的鋼筋應變；

5)假設一裂縫傳遞長度ltr，然后平均分為n等份，則每一段長度為ΔZ=ltr/n；

6)由已知的靜動態關系，進行數值積分求解。假設鋼筋應變增量和混凝土應變增量是相同的，由式(3)計算

(3)

式中：εs,0，εc,0分別代表鋼筋和混凝土在Type1類型下的應變值；εs,n，εc,n分別為鋼筋和混凝土在Type2類型下的應變值；0≤χi≤1，其中χi表示相似系數，現假設函數si作為χi功能函數，表示如下：

si=si-1-ΔZ[-χi(ss,0-ss,n+sc,0-sc,n)+ss,0-sc,0]

(4)

如果采用顯示有限差分法，可用式(5)計算鋼筋的應變值εs,i。

εs,i=εs, i-1-Δzi(4/φEs)τi-1

(5)

7)如果在第n個點時候，sn不等于0，改變ltr值并繼續步驟6)；

8)若在第n點時，εs,n≠fct/Ec，此時χi≠1，改變εs,0并返回到步驟2)。

給定一個裂縫寬度數值w，則可根據以上的程序及時相應的法向力N，同時可以計算裂縫的最大間距，sr,max=2ltr(最小值為ltr)。

3 模型應用

筆者所建立的計算模型可有效預測鋼筋混凝土梁橋裂縫開展模式，摸清裂縫的開裂間距和裂縫寬度。學者Mitch在1996年做過相關試驗，其中幾何屬性考慮了尺寸效應的影響，分別計算α=1和α=2的情況。當α=1的時候隨著荷載等級的增加，裂縫寬度的變化情況，如圖5。將文中的計算模型與Mitch計算模型進行了對比分析，驗證了該程序的合理性。可以用該方法有效地預測鋼筋混凝土梁的裂縫寬度。

圖5 文中計算模型與Mitch模型對比Fig.5 Comparison of calculation model and Mitch model

圖6為計算裂縫的傳遞長度和鋼筋應力之間的關系。裂縫傳遞長度隨著鋼筋應力的增加是逐漸減小，同時在相同鋼筋應力水平下，裂縫傳遞長度是隨著幾何尺寸變化而成比例關系變化的。當鋼筋應力達到屈服應力的時候，此時α=1和α=2時的裂縫傳遞長度的比值非常接近黃金分割率，如式(6)。因此，鋼筋混凝土梁的裂縫分布模式可以用黃金分割率來表達。

φ=α·16 mm，fc=34.9 MPa；B=α·170 mm，fct=1.8 MPa；H=α·95 mm，Ec=31 GPa；fy=400 MPa，Es=210 GPa；

[ltr(α=1)/ltr(α=2)]σs=400 MPa=189 mm/308 mm≈φ

(6)

由以上分析還可知，鋼筋混凝土梁的裂縫分布模式可以用黃金分割率來闡釋，同時可以得到當梁的幾何尺寸存在倍數關系的時候，裂縫的傳遞長度也將成倍數增加。

圖6 α=1和α=2時裂縫傳遞長度變化規律Fig.6 Law of crack propagation length when α=1and α=2

4 基于黃金分割點的裂縫評估

4.1 尺寸效應模型

裂縫間距隨著幾何尺寸的倍數變化表現出尺寸效應，S.BURTSCHER等[12]將其用冪函數形式表達為：

式中：D0為參考尺寸(α=1)；D為通用尺度(α>1)；Sr0為α=1時裂縫間距；Sr為α>1時裂縫間距；μ值可通過模型實驗或者數值模擬得到。

4.2 模型實驗與數值模擬

為計算μ值，筆者設計了3組鋼筋混凝土實驗梁，且根據相似原理[9]的比例關系保證3組梁的截面幾何相似，即高寬比一致。3組梁的梁高分別為900，600，300 mm，不同尺寸梁的截面配筋如圖7，加載方式采用四點彎曲實驗。

圖7 截面配筋Fig.7 Section reinforcement

實驗過程中分別記錄了3組實驗梁的裂縫寬度、裂縫間距、應變值、荷載大小等參數。3組梁的裂縫間距分別為43，24，13 cm；同時為了驗證模型實驗的可靠性，筆者通過大型通用有限元軟件ABAQUS分別模擬了3組實驗梁的破壞過程，數值模擬的參數取值與室內模型保持一致。有限元的計算結果如圖8，根據有限元計算結果統計3組梁的裂縫間距分別為41，20，12 cm。

圖8 數值模擬實驗梁裂縫分布Fig.8 Numerical simulation of fracture distribution of experimental beam

通過室內模型實驗與數值模擬驗證過程，可以得到結論：當鋼筋混凝土梁的幾何尺寸比例關系為D0/D≈0.5，裂縫傳遞長度比值符合黃金分割率特點，因此可以求得μ≈0.7。

總之，裂縫間距具有尺寸效應，更加簡單地研究裂縫的模式，通過縮尺模型預測大跨度橋梁的裂縫分布情況。

5 結 論

筆者探討了一種用于評價鋼筋混凝土梁橋裂縫分布模式的新方法。通過非線性數值模型計算可以得到裂縫間距的尺寸效應規律，結合實驗數據與數值模擬驗證可以得到以下結論：

1)鋼筋混凝土梁的裂縫分布模式可以用黃金分割率來表達，同時鋼筋混凝土梁的裂縫傳遞長度ltr具有尺寸效應。

2)當鋼筋混凝土梁幾何尺寸比例為D0/D≈0.5，裂縫傳遞長度比值符合黃金分割率特點，可以求得μ≈0.7。那么可結合實驗模型或數值模擬來預測鋼筋混凝土梁橋的裂縫分布情況。

[1] FANTILLI A P, FERRETTI D, IORI I, et al. Flexural deformability of reinforced concrete beams[J].JournalofStructuralEngineering,1998,124(9):1041-1049.

[2] HEJAZI M. Geometry in nature and Persian architecture[J].Building&Environment,2005,40(10):1413-1427.

[3] 陳輝.黃金分割在平面設計中的研究[D].石家莊：河北師范大學，2011. CHEN Hui.TheResearchonGoldenSectioninGraphicDesign[D]. Shijiazhuang: Hebei Normal University, 2011.

[4] BAZANT Z P. Size effect in blunt fracture: concrete, rock, metal[J].JournalofEngineeringMechanics,1984,110(4):518-535.

[5] 張奔牛，范中華，黃銳，等.基于機敏網的混凝土結構裂縫寬度監測方法研究[J].重慶交通大學學報(自然科學版),2014,33(2):26-29. ZHANG Benniu,FAN Zhonghua,HUANG Rui,et al. Crack width monitoring of concrete structures based on smart film[J].JournalofChongqingJiaotongUniversity(NaturalScience),2014,33(2):26-29.

[6] 王家偉,楊庭庭,蔣偉, 基于微分方程的橋梁裂縫檢測研究[J].重慶交通大學學報(自然科學版),2014,33(5):32-35. WANG Jiawei, YANG Tingting, JIANG Wei. Bridge crack detection based on differential equations[J].JournalofChongqingJiaotongUniversity(NaturalScience),2014,33(5):32-35.

[7] CARPINTERI A, CHIAIA B, FERRO G. Size effects on nominal strength of concrete structures: multifractality of material ligaments and dimensional transition from order to disorder[J].Materials&Structures,1995,28(6):311- 317.

[8] BEEBY A W. The influence of the parameterφ/ρeff on crack widths. Discussion[J].StructuralConcrete,2004,5(2):71-83.

[9] 楊俊杰.相似理論與結構模型實驗[M].武漢：武漢理工大學出版社,2005:10-13. YANG Junjie.SimilarityTheoryandStructuralModelExperiment[M]. Wuhan: Wuhan University of Technology Press,2005:10-13.

[10] MOORMAN C M, GOFF J E. Golden ratio in a coupled-oscillator problem[J].EuropeanJournalofPhysics,2007,28(5):897-902.

[11] YI Zhijian, WANG Shijie, WANG Xiangjian. Precise solutions of elastic-plastic crack line fields for cracked plate loaded by antiplane point forces[J].EngineeringFractureMechanics,1997,57(1):75-83.

[12] BURTSCHER S, CHIAIA B, DEMPSEY J P, et al. RILEM TC QFS quasibrittle fracture scaling and size effect’—final report[J].Materials&Structures,2004,37(8):547-568.

Study on the Crack Pattern of RC Beam Bridge Based on Gold-division Ratio Model

SONG Jun1, ZHOU Jianting2, WANG Mingbin1, JIANG Rui1

(1. School of Civil Engineering, Ludong University, Yantai 264025, Shandong, P.R.China; 2. School of Civil Engineering, Chongqing Jiaotong University, Chongqing 400074, P.R.China)

A gold-division ratio was first introduced as a new approach to evaluate the crack distribution pattern for RC beam bridge.The crack opening and space of cracked concrete was predicted by establishing a concrete “single rebar tension model” and by compiling procedures and finally the accuracy of the obtained parameters were verified by conducting model experiment and numerical simulating. The results of above study show that application of gold-division ratio in analyzing crack opening and space of cracked concrete is of profound physical significance and the research results also reveal that crack spacing of concrete beam is of size effect. The significance of this given method lies that scale model can be used to predict the crack distribution pattern of large bridges and thus provides guidance to safety assessment of concrete bridge.

bridge engineering; crack mode; golden ratio; size effect

10.3969/j.issn.1674-0696.2016.05.03

2016-01-06；

2016-02-29

國家自然科學基金項目(55150826，E080505)；山東省高校科技計劃項目(J16LG60，J15LG01)

宋 軍(1982—)，男，山東威海人，講師，博士，主要從事橋梁設計理論與工程控制方面的研究。E-mail:songjun198298@163.com。

U447

A

1674-0696(2016)05-009-04