周期沖擊下簇生離散混合沖擊模型的可靠性分析
姜培華
(安徽工程大學 數理學院,安徽 蕪湖 241000)
?
周期沖擊下簇生離散混合沖擊模型的可靠性分析
姜培華
(安徽工程大學 數理學院,安徽 蕪湖241000)
摘要:建立一類簇生離散混合沖擊模型。假定沖擊按周期來到,每個周期的沖擊次數服從獨立同分布的二項隨機變量,沖擊強度服從獨立同分布的離散隨機變量。首先在混合沖擊模型下給出系統壽命的定義,研究系統壽命的生存函數、平均壽命,并給出其概率分布和遞推公式;其次定義了系統失效時所經歷的具有非零沖擊量的周期數和系統失效時所遭受的沖擊強度總和等可靠性指標,推導并給出這些指標概率分布的遞推公式和期望表達式;最后在周期沖擊次數服從0-1分布、沖擊強度服從幾何分布下,給出了混合沖擊模型相關可靠性指標的數值分析過程。
關鍵詞:混合沖擊模型;生存函數;壽命分布;平均壽命;周期沖擊;沖擊總量;簇生
沖擊模型是可靠性理論中一類重要的隨機數學模型。起初沖擊模型常用來刻畫隨機環境下工程系統的壽命規律,隨著研究的推廣,它的應用涉及更多領域,如物理、醫學、交通、財政和保險等。沖擊模型研究的主要內容是系統的壽命規律、平均沖擊量和系統的失效概率,基于系統失效機制,可分為兩類基本模型[1-2]:① 假定沖擊強度具有累積效果,若逐次沖擊強度的累積值超過系統的極限值則導致系統失效,稱為累積模型;② 假定沖擊強度無累積效果,若單個“大”的沖擊強度超過系統的極限值則導致系統失效,稱為極端模型。文獻[3-4]分別研究了基礎過程為Poisson過程和Poisson-Geometric過程的累積沖擊模型的可靠性指標。對于沖擊模型研究的其他主要問題參見文獻[5-9]。在沖擊模型的以往研究中大都關注沖擊間隔和沖擊強度服從連續分布的情形,也就是假定連續兩次相鄰沖擊的時間間隔服從一連續概率分布,沖擊強度是一組獨立同分布的連續隨機變量。對于離散沖擊模型(沖擊間隔和沖擊強度均服從離散型分布)的研究文獻相對較少,一些關于離散模型的研究成果見文獻[10-12]。
在很多情形下系統遭受的沖擊并不是逐個到來的點過程,而是在每一個來到時間點上同時存在隨機個數的不同的沖擊。本文考慮一類周期沖擊下的簇生離散模型,沖擊源按周期到來,周期可以理解為1個單位時間,如1 h、1 d或1 w等。在單個周期可能會同時釋放若干個沖擊,周期內的每個沖擊以一定的概率(比如p)發生,每個周期發生的沖擊次數是一組獨立同分布的離散隨機變量。假定沖擊強度和沖擊來到過程是獨立的。
Xj表示系統在第j個周期內遭受的沖擊次數,且諸Xj獨立同分布于參數為(r,p)的二項分布。Bji表示第j個周期內的第i次沖擊的強度,假定諸沖擊強度Bji都是獨立同分布的離散隨機變量,且具有累積概率分布函數FB(x)和概率分布列fB(x),則第j個周期的沖擊強度總量和前n個周期的沖擊強度總量可分別表示為:
在沖擊量可累積情況下,給定系統沖擊的極限值k,則累積模型系統失效的等待時間(系統壽命)為
(1)
在極端沖擊情況下,給定系統瞬時沖擊極限值m,則極端模型系統失效的等待時間(系統壽命)為
Tm=min{n:Mn>m}
(2)
其中Mn=max{A1,A2,…,An}。
考慮到Xj(j=1,2,…)與Bji(j=1,2,…;i=1,2,…,r)都是獨立同分布的,從而可得每個周期的沖擊總量Aj(j=1,2,…)也是獨立同分布的,其累積概率分布函數和概率分布列可分別表示為:
(3)
(4)
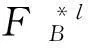
1混合沖擊模型
將累積模型和極端值模型結合于同一個系統,建立具有下述機制的混合沖擊模型:沖擊的單獨作用和累積作用均對系統產生影響。如果一個足夠“大”的沖擊強度超過系統瞬時極限值m,或多個“不太大”沖擊的累積強度超過系統累積極限值k,系統都會失效。失效時間取決于二者中較早來到者,故混合沖擊模型系統失效的等待時間(系統壽命)為
(5)
當k≤m時,混合沖擊模型就是累積沖擊模型。因此本研究重點討論當k>m時混合沖擊模型的相關性質和結果。
定理1對于k>m≥1和n≥1,混合沖擊模型的系統壽命Zk,m的生存函數為
其中P{Zk,m>0}=1。
證明對于k>m≥1和n≥1,由Zk,m的定義可知
對In取條件可得
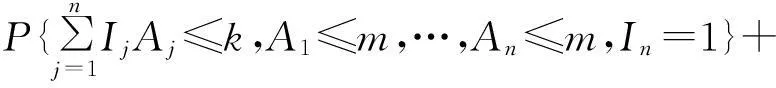
故結論成立。
系統的平均壽命是表征系統好壞的一個重要的可靠性指標,下述推論給出了系統平均壽命E(Zk,m)的遞推表達式。
推論1對于k>m≥1,在混合沖擊模型下系統的平均壽命為
其中E(Z0,m)=[1-(1-p)r]-1。
證明由定理1可得,E(Zk,m)可表示為
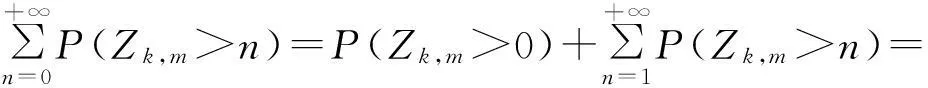
移項整理即得
為了更好地描述系統的壽命特征,對于k>0,m>0,定義如下3個隨機變量:
其中:Ij是一個貝努利隨機變量,且E(Ij)=1-(1-p)r;N(Zk,m)表示在混合模型下系統失效時所經歷的具有非零沖擊量的周期個數;S(Zk,m)表示在混合模型下系統失效時所遭受的沖擊總量。
定理2對于k>m≥1和n≥1,隨機變量N(Zk,m)的分布律為
其中φ(n,s,k,m)滿足如下遞推公式:
證明對Zk,m取條件有
又
記φ(n,s,k,m)=P{N(s)=n,Zk,m>s},則有
對Is取條件可得
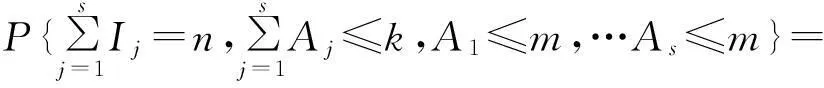
A1≤m,…,As-1≤m,a≤m}fA(a)+
(1-p)rP{N(s-1)=n,Wk,m>s-1}=
另一方面,對Is取條件有

[1-(1-p)r]P{N(s-1)=n-1,Zk,m>s-1}+
(1-p)rP{N(s-1)=n,Zk,m>s-1}=
[1-(1-p)r]φ(n-1,s-1,k,m)+(1-p)rφ(n,s-1,k,m)
綜上可知定理2成立。
定理3在混合沖擊模型下,系統失效時所遭受的沖擊總量S(Zk,m)的分布律為:
當s>k,有
當m 其中Φ(n,s,m)滿足如下遞推公式: 證明為了便于書寫和證明,記Φ(n,s,m)=P{S(n)=s,Tm>n},由S(Zk,m)的定義可得 當s>k時,對In取條件有 類似地,當m 關于Φ(n,s,m),對In取條件有 Φ(n,s,m)=P{S(n)=s,A1≤m,…,An≤m}= [1-(1-p)r]P{S(n-1)=s-An,A1≤m,…,An≤m}+ (1-p)rP{S(n-1)=s,A1≤m,…,An-1≤m}= (1-p)rP{S(n-1)=s,A1≤m,…,An-1≤m}= 綜合上述兩種情況定理3成立。 根據隨機變量N(Zk,m)和S(Zk,m)的定義,利用瓦爾德定理易知下述推論成立。 推論3對于k>m>0,r>1,隨機變量N(Zk,m)和S(Zk,m)的期望如下: 2數值算例 本節利用Matlab軟件,在給定沖擊強度Bji和單周期內沖擊次數Xj的概率分布下,分析了混合模型下系統的3個可靠性指標的變化情況,為了便于計算,作如下簡化: 1) 假定單周期內的沖擊次數Xj服從概率為p的貝努利分布,此時的沖擊強度Bji可以簡記為Bj,從而相應的3個指標可以簡化為: 2) 假定每次的沖擊量Bj服從發生率為θ的幾何分布,對于任意的j沖擊量Bj都是獨立同分布的,且與沖擊次數Xj和沖擊來到過程均獨立。 3) 根據假設1)和2)有 在p=0.05,0.1和θ=0.125,0.2以及(k,m)=(5,3),(10,3),(10,5),(20,5)下,計算得出E(Zk,m),E[N(Zk,m)]和E[S(Zk,m)]的結果,見表1。分析表1可知: 1) 當沖擊極限值(k,m)增大時,系統平均壽命就增大。當給定系統沖擊極限值(k,m)時,發生概率p增大,則系統平均壽命減小。 2) 當沖擊量Bj的概率分布給定時,系統失效時所遭受的非零沖擊的平均周期數E[N(Zk,m)]和失效時所遭受的平均沖擊總量E[S(Zk,m)]保持不變,且與發生概率p無關。 表1 幾何沖擊下混合模型指標的數值分析 3結束語 目前,關于連續型沖擊模型的研究比較成熟,但關于離散型沖擊模型的研究相對較少。本文假定沖擊按固定周期來到,在每個周期末會產生若干個不同的沖擊,每個周期發生的沖擊次數是獨立同分布的二項隨機變量序列,每次的沖擊強度是獨立同分布的離散隨機變量序列,沖擊來到過程、單周期的沖擊次數和沖擊強度三者相互獨立。在上述假設下研究了混合沖擊模型的壽命分布、平均壽命、系統失效時所經歷的具有非零沖擊量的周期個數以及系統失效時所遭受的沖擊總量等可靠性指標。給出了系統壽命的生存函數和平均壽命的遞推公式、非零周期數和沖擊總量兩個指標的概率分布遞推公式和期望的表達式。最后,在給定沖擊強度服從幾何分布、單周期內沖擊次數服從貝努利分布下,分析了混合模型下系統的3個可靠性指標的變化情況,并給出相應結論。 參考文獻: [1]李澤慧,白建明,孔新兵.沖擊模型:進展與應用[J].數學進展,2007,36(4): 385-398. [2]李澤慧,黃寶勝.一種沖擊源下沖擊模型的壽命分布及性質[J].蘭州大學學報(自然科學版),1999,35(4):1-7. [3]王丙參,魏艷華,戴寧.損傷可加沖擊模型的可靠性指標[J].北京聯合大學學報(自然科學版),2012,26(1):66-69. [4]王丙參,李艷穎,常振海.Poisson-Geometric過程在可靠性理論中的應用[J].齊齊哈爾大學學報,2012,28(3):83-85. [5]BAI J M,LI Z H,KONG X B.Generalized shock models based on a cluster point process[J].IEEE Transactions on Reliability,2006,55(3):542-550. [6]ERYILMAZ S.Generalizedδ-shock model via runs[J].Statistics and Probability Letters,2012,82(2):326-331. [7]FINKELSTEIN M F.Marais.On terminating Poisson processes in some shock models[J].Reliability Engineering and System Safety,2010,95(4):874-879. [8]MALLOR F E.Omey.Shocks,runs and random sums[J].Journal of Applied Probability,2001,38(2):438-448. [9]SUMITA U J,SHANTHIKUMAR G.A class of correlated cumulative shock models[J].Advances in Applied Probability,1985,17(2):347-366. [10]AVEN T,GARDER S.Optimal replacement in a shock model:discrete time[J].Journal of Applied Probability,1987,24(1):281-287. [11]GUT A.Mixed shock models[J].Bernoulli,2001,7(3):541-555. [12]ERYILMAZ S.On the lifetime behavior of discrete time shock model[J].Journal of Computational and Applied Mathematics,2013,237(1):384-388. (責任編輯何杰玲) Reliability Analysis of a Mixed Model Under Clustered Discrete Shocks of Periodical Arrival JIANG Pei-hua (School of Mathematics and Physics, Anhui Polytechnic University, Wuhu 241000, China) Abstract:A class of discrete clusters of mixed shock model was established, assuming that the shock came in cycles and in each cycle the number of shocks were independent and identically distributed random variables with binomial distribution, and the shock intensity impact obeyed discrete random variables. First, under the mixed shock model, the system’s lifetime was defined, the survival function and expectation of the system’s lifetime were studied, and their probability distribution and recursive formulas were also given. Secondly, we defined the number of periods in which the system has a non-zero amount of shock during failure and the amount of total shocks which the system suffered by the failure time. Furthermore the recursive formula expressions about the probability distribution and the expectation of those indexes were derived. Finally, assuming that the number of shocks in a period obeyed 0-1 distribution and the shock intensity followed geometric distribution, we given a numerical analysis of the relevant reliability index. Key words:mixed shock model; survival function; lifetime distribution; mean lifetime; periodic shock; total shocks; cluster 文章編號:1674-8425(2016)04-0154-07 中圖分類號:O211.4 文獻標識碼:A doi:10.3969/j.issn.1674-8425(z).2016.04.026 作者簡介:姜培華(1979—),男,山東曹縣人,碩士,講師,主要從事概率統計和隨機過程研究。 基金項目:國家自然科學基金資助項目(11401006);安徽省自然科學基金資助項目(1208085QA04);2015年安徽省高等教育提升計劃省級自然科學研究一般項目(TSKJ2015B29) 收稿日期:2015-10-21 引用格式:姜培華.周期沖擊下簇生離散混合沖擊模型的可靠性分析[J].重慶理工大學學報(自然科學),2016(4):154-160. Citation format:JIANG Pei-hua.Reliability Analysis of a Mixed Model Under Clustered Discrete Shocks of Periodical Arrival[J].Journal of Chongqing University of Technology(Natural Science),2016(4):154-160.