楊輝三角與志最短路線

蔣明玉

同學們知道楊輝三角嗎？看看蔣老師怎么介紹吧。

同學們，請仔細觀察一下圖1，你覺得它像什么圖形？對了，它像一個用數組成的等腰三角形，

你能發現這些數之間的規律嗎？其實，最本質的特征是，數1在兩條腰上，而其余的數則等于其“肩”上的兩個數之和，如第六層的第二個數5，就等于其“肩”上的兩個數1、4的和.

這個三角我們叫楊輝三角，它出現在我國南宋數學家楊輝編著的《詳解九章算法》一書中，楊輝指出這個方法出于《釋鎖算術》.在歐洲，這個三角被認為是法國數學家、物理學家帕斯卡首先發現的，被稱為帕斯卡三角，

下面讓我們在解決一些走最短路線的問題中找一找楊輝三角.

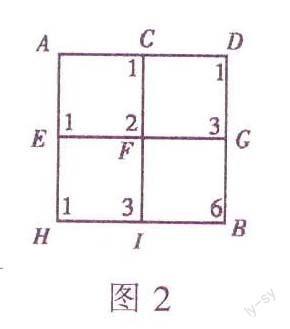
據說楊輝研究數學達到了如醉如癡的境界，他也非常喜歡和友人們一起研究數學問題.一天，他的一位友人甲邀請他一起討論數學問題.楊輝有一張地圖，如圖2，地圖上標明了從楊輝家（A）去友人甲家（B）的每條路線.楊輝發現地圖上的好幾條到友人甲家的路線都是最短的，而且都不會重復.同學們知道一共有幾條最短路線嗎？

想要搞清楚路線，先得確定從A點到B點的最短路線到底是多長，然后確定走的方向，為了保證不走“回頭路”，只能向右或向下走.

有些同學很快找出了從A點到B點的

通過驗證，我們確信這六條路線都是從A點到B點的最短路線.如果按照上述方法找，它的缺點是不能保證找出所有的最短路線.當然如果圖形更復雜些，做到不重復也是很困難的.

那么，解決這樣的問題是否有規律可循？讓我們一起往下看.

1.看C點：從A點到C點，只有一條最短路線，同樣道理，從A點到D點、從A點到E點、從A點到H點也都只有一條最短路線.

我們把數字“1”分別標在C、D、E、H這四個點上，如圖2.，的三條最短路線.

現在再讓我們來觀察圖2.如果我們把圖2加上對角線，再把它旋轉一下，就會發現它是楊輝三角的一部分，如圖3.

這樣，我們就可以運用楊輝三角來解決這種問題，既簡單又準確.讓我們再來試一試，

圖4是一個由18個相同的小等腰直角三角形拼成的平行四邊形，有一只螞蟻從A點出發，沿圖上的線段爬行到曰點，請求出這樣爬行的最短路線有幾條，

同學們能根據楊輝三角解決這個問題嗎？

我們只要對應地寫出楊輝三角，就知道爬行的最短路線有20條.