星載微波輻射計分辨率匹配的平滑參數選擇

王兆徽 廖菲 宋清濤 劉宇昕

（1國家衛星海洋應用中心，北京 100081）（2國家海洋局空間海洋遙感與應用研究重點實驗室，北京 100081）（3中國氣象局廣州熱帶海洋氣象研究所，廣州 510080）（4廣州市氣象臺，廣州 511430）

星載微波輻射計分辨率匹配的平滑參數選擇

王兆徽1，2廖菲3，4宋清濤1，2劉宇昕1，2

（1國家衛星海洋應用中心，北京 100081）（2國家海洋局空間海洋遙感與應用研究重點實驗室，北京 100081）（3中國氣象局廣州熱帶海洋氣象研究所，廣州 510080）（4廣州市氣象臺，廣州 511430）

為了反演獲得準確的大氣海洋參數，須要將星載微波輻射計分辨率不同的觀測亮溫進行分辨率統一的重采樣處理。結合衛星的相關參數，使用漸削圓形口徑和正軸等距投影的方式對星載微波輻射計的天線方向圖進行仿真模擬。使用Backus－Gilbert方法對包含地理信息的模擬天線方向圖以及AMSR－E真實數據進行觀測亮溫重采樣試驗，并分析了調整平滑參數時匹配誤差和噪聲參數兩個關鍵指標的變化，得出選定的最佳平滑參數是當平滑參數從0向無窮大變化時，首次出現構造天線方向圖非負的平滑參數。試驗表明，目前常用的固定濾波分辨率匹配方法結果較好且計算效率高，具有一定的應用價值。

海洋衛星；星載微波輻射計；先進掃描微波輻射計；分辨率匹配；Backus－Gilbert算法

1 引言

星載微波輻射計可以測量地表輻射出的電磁波。通過對其觀測數據進行反演處理，可以有效地獲取海面溫度、海面風速、大氣中的水汽含量、云液態水含量等海洋大氣參數。這些信息的綜合應用在全球氣候變化、海洋環境預報、海況監測、海洋災害防護、海上維權執法等領域具有重要的意義。星載微波輻射計分辨率匹配的方法也被稱為重采樣，是對其不同波段不同空間分辨率的數據進行分辨率統一的處理，這一數據處理過程不僅能夠為后續的反演工作提供可靠的數據，還能夠對衛星載荷設計和輻射定標等先期工作提供技術指標要求。

重采樣通常有兩個分辨率統一的方向：將高空間分辨率數據重采樣為低空間分辨率數據；將低空間分辨率數據重采樣為高空間分辨率數據。兩者中，前者會導致數據信息的部分丟失；后者會引入大量噪聲并降低觀測精度。業務化應用中，多采用將高空間分辨率數據匹配至低空間分辨率的方法。通常認為，高頻數據具有較高的空間分辨率，包含更豐富的細節。

許多重采樣的研究都使用了Backus和Gilbert［1－2］提出的基于矩陣反演技術的方法。該方法一開始用于解決從有限的不太精確的地球數據中建立地球模型的反演問題，實質是一類有關非唯一性的數學問題。Stogryn［3］首先將Backus－Gilbert方法（簡稱BG方法）引入了微波遙感領域。之后，國內外的許多學者也展開了相應的研究［4－9］。

本文以搭載于地球觀測系統－水衛星（EOS Aqua）的先進掃描微波輻射計（Advanced Microwave Scanning Radiometer，AMSR－E）［10］為例進行試驗，討論了美國遙感系統公司（Remote Sensing System，RSS）提出的重采樣中平滑參數調節方法［11］的合理性，分析了BG方法中平滑參數的改變對重采樣結果的影響，以及觀測噪聲對重采樣結果的影響。合理的使用重采樣方法能夠有效地提高反演產品的精度。目前，該基于BG的觀測亮溫重采樣方法正應用于我國海洋二號衛星掃描微波輻射計的L1數據重處理過程，這不僅為儀器的在軌定標工作提供了參考依據，還為后續的海面溫度、海面風速、水汽含量和液水含量的反演工作以及其他業務化專題圖的制作提供了可靠的數據。

2 衛星觀測的仿真模擬

仿真試驗基于AMSR－E的儀器參數，分為6．925GHz、10．65GHz、18．7GHz、23．8GHz和36．5GHz 5個頻段模擬了天線方向圖、單次觀測的天線增益以及觀測幾何。微波輻射計的天線增益在很多研究中，選取為高斯函數［12］，或者是辛格函數［13］進行表示，兩者具有相似的結果。選用高斯函數的優點是增益的立體角積分為定值π，便于歸一化處理。而辛格函數和實際的天線增益分布更相近。微波輻射計的天線系統通常是反射器系統，使用漸削圓形口徑模型［14］和主波束效率等儀器參數，可以很好地模擬天線增益分布，如圖1所示。

將天線增益的立體角積分轉變為地表的面積積分是天線應用的常用方式，過程可以分為單次觀測天線方向圖的地表投影和觀測幾何分布，如圖2所示。試驗中采用如下地圖投影規則（圖3）：將圖像中心變換至三維球坐標處，再進行正軸等距投影［15］。300km×300km平面矩形區域的幾何中心投影至赤道的正軸等距投影，其圖像變形小于投影至地球表面其他位置。這種情況下，二維坐標內距原點最遠的點到原點距離為212．13km；三維坐標內其球面距離為212．11km。

圖2 5個不同頻率的單次觀測地表天線方向圖Fig．2 Single observation of antenna pattern on earth surface at 5different frequencies

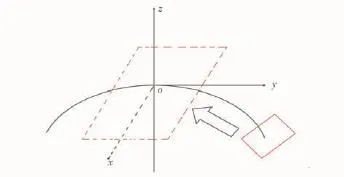
圖3 正軸等距投影坐標轉換Fig．3 Positive axis equidistant projection coordinate transformation

為了獲得觀測幾何，假設衛星運動是簡單的二體問題，采用太陽同步回歸圓軌道［16］和歐拉角旋轉［17］。圖4是使用模擬的地理數據（藍線）與AMSRE 2010年5月2日20：05的升軌的觀測點位置（紅點）比較。結果顯示，仿真實驗的結果與真實數據十分接近。

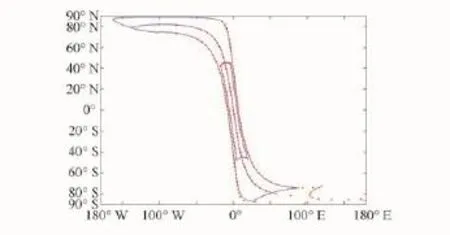
圖4 AMSR－E觀測點位置（紅）和仿真數據（藍）的比較Fig．4 Comparaison between real observation（red）and simulated data（blue）for AMSR－E

3 BG方法觀測亮溫重采樣原理

在天線端，亮溫可以表示為天線增益與地表輻射的形式［11］：

式中：Ti（ρ）表示位置向量為ρ的地表輻射；Gi（ρ）表示某一特定觀測的歸一化天線增益；dA表示積分為地表面積積分。文中下標i均表示參與運算的第i個觀測亮溫。

Stogryn采用Backus－Gilbert方法從數學上構造了某一特定點ρ0的亮溫TB（ρ0）與TBi之間的關系，即使用線性的表示方法近似地表示TB（ρ0）。因此可以構造出式（2）的亮溫表達式，N為參與運算的共N個亮溫數據，ai為系數，其中中括號的部分也被稱為構造天線方向圖。

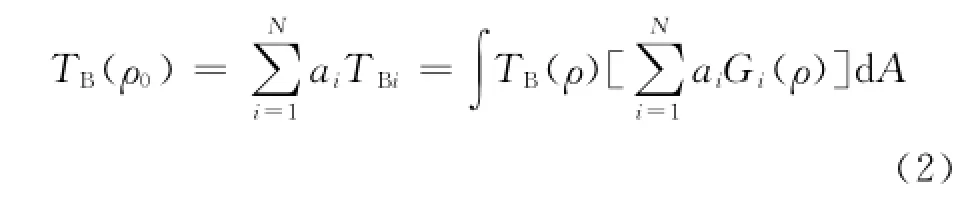
解決重采樣問題的關鍵是獲得系數ai，這須要考慮構造天線方向圖是否合理。一種直觀常用的最小化目標函數如（3）式所示。F（ρ）通常被稱為目標天線方向圖或理想方向圖，用來標定重采樣目標；Q被稱為匹配誤差（fit error）。

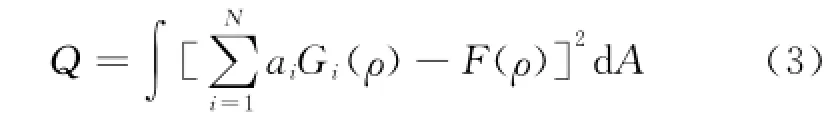
除了構造天線方向圖的選取之外，測量本身的誤差同樣須要注意：實際上，天線溫度總是被隨機噪聲所污染。假設噪聲的方差為ΔT，均值為0，那么重采樣中由測量誤差造成的包含權重的方差為

式中：a是重采樣系數ai構成的N列列矩陣；E是衛星觀測值的協方差矩陣。如果N個觀測值互相獨立且儀器狀態不發生變化，那么E就是一個對角元素為ΔT的對角陣。式（4）表示了觀測誤差在重采樣時的引入程度，系數a起到對各個觀測誤差所占比重的分配——這在觀測值不互相獨立時或觀測值噪聲方差不同時更容易理解。因此定義與觀測噪聲無關的噪聲參數（noise factor）為

重采樣理想的結果是構造天線方向圖與理想方向圖十分接近，且觀測誤差放大最小。一般來說，這兩點是矛盾的。AMSR的Level 2A算法引入β平滑參數（smoothing parameter）和方差對匹配誤差進行修正：

最小化式（6），可以方便地獲得重采樣系數的解析解。其中j，v均是N列列矩陣；V，H均為N行N列的矩陣：

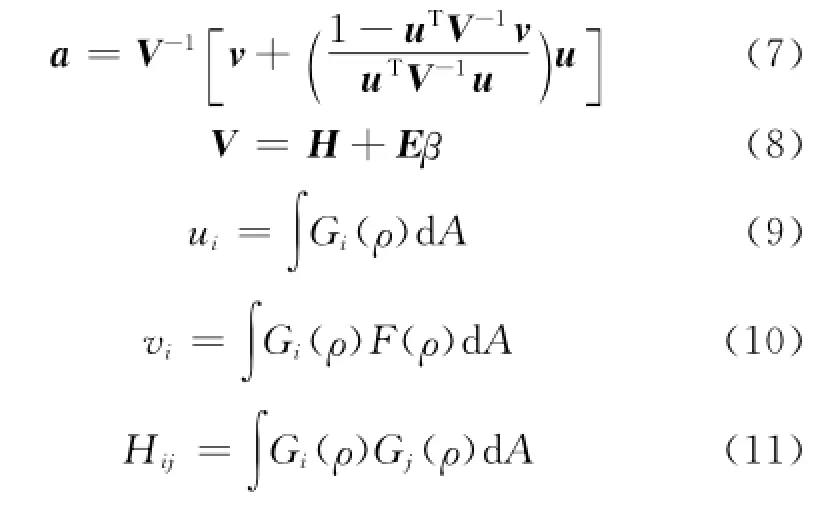
4 BG方法的平滑參數選擇

4．1 重采樣誤差來源

構造亮溫TB準確程度的評價主要從兩個方面進行：一是目標天線方向圖與構造天線方向圖之間的匹配程度，二是測量本身誤差的引入程度。目標方向圖與構造天線方向圖的差異，當背景場的輻射分布是自相關且有類似歸一化的功率密度譜［4］時，可以寫為如下形式。其中J是比例系數。

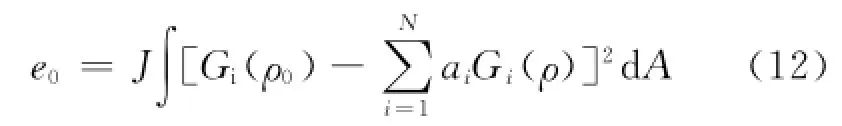
許多學者使用真實的高分辨率溫度場進行重采樣結果的評定，如Poe［4］，Robinson［5］，Farrar和 Smith［18］；另一些學者使用模擬的溫度場，如Robinson［5］，王永前［6］等。但是，無論采用哪種溫度場，都是以特定的溫度場分布來評價重采樣結果的好壞，對于全球范圍的研究，難免會具有局限性。與之相比，式（12）的宏觀意義更明確。

測量本身誤差的引入，體現為噪聲參數。這項誤差完全由系數a決定，與溫度場的選擇無關，更容易進行數值的計算。

4．2 平滑參數的選取

試驗中我們根據經驗令ΔT的數值為0．18，它并不影響最終的結果，僅僅相當于對平滑參數附加了一個比例變化。通常情況匹配誤差和噪聲參數并不是一個數量級。為了方便比較，我們令（12）式中的比例系數J＝1×104。

平滑參數、噪聲參數和匹配誤差之間有一個明顯的單調變化關系，圖5展示了將36．5GHz分辨率的觀測亮溫重采樣為18．7GHz分辨率的觀測亮溫時，升軌近赤道掃描帶正中點這三者的變化：平滑參數的變大導致噪聲參數變小，噪聲參數變小導致匹配誤差變大。這是由于系數a滿足。平滑參數的變大導致（7）式中的V的數值分布與對角陣更相似，進而使a的分布更平均，體現為噪聲參數的變小；噪聲參數變小（a的分布更平均），使式（12）中的與Gi（ρ0）偏離程度更大。

匹配誤差總認為是越小越好，這一點由其物理意義明確的決定。噪聲參數可以視為系數分布的特征，形式上是二次冪平均。根據柯西不等式，有

綜合圖4中平滑參數、噪聲參數和誤差之間的關系，可以得到這樣簡明的結論：平滑參數的增大導致了重采樣結果的變壞。因此結合天線方向圖的非負特性，一個合理選定平滑參數的方法是：當平滑參數從0向無窮大變化時，首次出現構造天線方向圖非負的平滑參數即為最佳平滑參數。

5 重采樣結果分析

使用36．5GHz和18．7GHz的仿真數據進行試驗，分析了觀測幾何的變化、觀測噪聲對重采樣結果的影響，以及目前常用的固定窗口濾波的結果。這兩個通道的地表天線方向圖面積最小，計算簡便。為了方便后續說明，約定了計數規則，展示在圖6中：obs8、obs122、obs236是一軌數據中最具代表性的三個數據帶，分別表示每一個掃描周期的第8個觀測數據（臨近一個掃描周期起始的觀測點e）、第122個觀測數據（一個掃描周期的中間觀測點f）、第236個觀測數據（臨近一個掃描周期結束的觀測點g）。

5．1 觀測幾何對重采樣結果的影響

挑選了7個典型區域分析觀測幾何對星載微波輻射計重采樣結果的影響。這種影響的根本原因是圓錐掃描的觀測方式和地球自轉線速度的經向差異。這二者中，前者是造成觀測幾何緯向形變的主要原因，后者是造成觀測幾何經向形變的唯一原因。

圖7為7個典型區域平滑參數為0時的噪聲參數、誤差以及最佳平滑參數時的噪聲參數、誤差，其中圖7（a）～（d）橫軸為某一特定掃描周期內觀測點計數，圖7（e）～（g）橫軸為從南極開始每一掃描周期選擇一個觀測點的計數。明顯看出，噪聲參數和誤差的緯向變化較大，且變化規律基本相同；經向變化在一條觀測帶的兩端較大，中心部位較小，且在南北極之間近似為線性關系。

5．2 觀測噪聲對重采樣結果的影響

可以通過對平滑參數在不同區域的變化進行討論，確定選取最佳平滑參數時對重采樣結果的影響。圖8中三個區域平滑參數的變化與圖7中平滑參數為0時的誤差（藍虛線）和最佳平滑參數時的誤差（紅虛線）的變化規律一致。

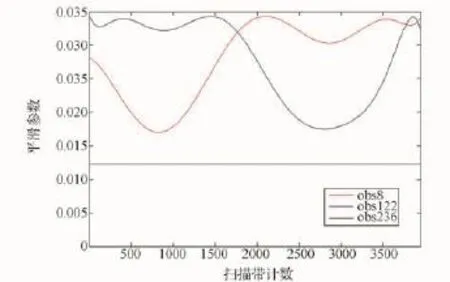
圖8 3個區域的平滑參數變化Fig．8 Changing of smooth factors in 3different zones

值得注意的是，平滑參數的變化范圍普遍在0．01數量級，也說明觀測噪聲縮小至1/100仍舊會對重采樣結果產生直接的影響。根據現有工程技術水平，觀測噪聲的減小并不能十分有效地改善BG算法重采樣的結果——當然，觀測噪聲的降低能夠提高觀測數據本身的數據質量。

5．3 BG方法誤差分析

圖9中，固定窗口濾波（藍虛線）是目前業務化最常用的濾波方式，試驗中窗口是以升軌obs122距赤道最近的觀測點為重采樣中心計算的重采樣系數。真實濾波，即準確計算各個觀測窗口的重采樣系數的濾波方法，也就是圖7中的最佳平滑誤差的結果。除此之外，固定濾波方法會出現構造天線方向圖小于0的情況，這樣的結果是沒有物理意義的。

固定窗口濾波的業務化應用雖然操作簡便，但是具有明顯的局限性：在每個掃描帶的obs122附近誤差最小，尤其是升軌過赤道區域；緯向誤差變化率特別大；經向誤差變化率相對其緯向誤差變化率較小，但仍不可忽略。最重要的是，使用固定窗口濾波會出現大量沒有物理意義的構造天線方向圖（圖9的a、b、c、d）。

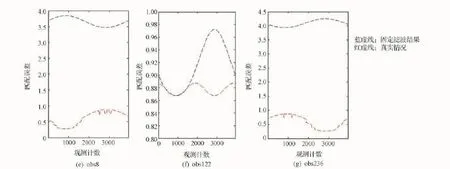
圖9 BG方法重采樣的結果Fig．9 Results of BG resampling method

6 星載微波輻射計真實數據的重采樣結果

使用固定窗口濾波對AMSR－E數據（2010年5月1日），進行36．5GHz分辨率的水平極化亮溫重采樣為18．7GHz分辨率的結果（如圖10所示），15°S至30°S之間的區域可以看出二者明顯的區別。須要特別注意的是：根據分析，固定窗口濾波的重采樣結果除了在掃描帶中部之外，其余位置僅僅在數值上是近似正確的，失去了物理意義。

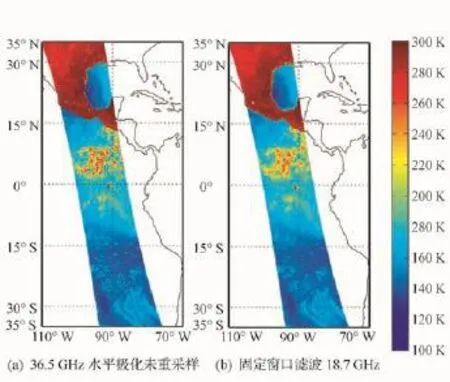
圖10 36．5GHz水平極化觀測亮溫重采樣Fig．10 Resampling for 36．5GHz h－pol brightness temperature

7 結束語

使用BG方法對模擬的星載微波輻射計軌道參數和儀器參數以及AMSR－E實測數據進行了觀測亮溫重采樣的工作，并討論了重采樣誤差的來源，分析了使用BG方法時最優平滑參數的選擇。通過分析發現，硬件設備和計算算法兩方面都會對重采樣的結果產生影響：①硬件方面，降低儀器的觀測噪聲可以直接提高觀測數據的質量，而儀器的觀測方式對重采樣的影響更大。②在計算算法方面，使用BG方法的固定濾波重采樣計算效率較高，有很好的應用前景。目前我國的海洋二號衛星掃描微波輻射計的L1數據正在使用這種方法進行數據重處理工作。然而這種方法仍有誤差較大、構造天線方向圖物理意義不明確等不足之處。考慮到在業務化工作中，采用實時數據的真實濾波進行重采樣運算，由于計算效率的低下并不具有應用價值。中國未來的海洋衛星發射計劃包括一系列的微波輻射計，以及鹽度試驗衛星［19］，為大洋環流、海氣相互作用、海水蒸發與降水平衡等方面的研究提供重要的數據。屆時，使用BG方法的固定濾波重采樣將會有更好的應用平臺。同時，基于新的載荷也會研發考慮到衛星觀測幾何變化的重采樣方法，期望新方法能夠具有較高計算效率和更高的精度。

（

）

［1］Backus G，Gilbert F．The resolving power of gross earth data［J］．Geophysical Journal International，1968，16（2）：169－205

［2］Backus G，Gilbert F．Uniqueness in the inversion of inaccurate gross earth data［J］．Philosophical Transactions of the Royal Society of London，1970，266（1173）：123－192

［3］Stogryn A．Estimates of brightness temperatures from scanning radiometer data［J］．Antennas and Propagation，IEEE Transactions on，1978，26（5）：720－726

［4］Poe G A．Optimum interpolation of imaging microwave radiometer data［J］．Geoscience and Remote Sensing，IEEE Transactions on，1990（5）：800－810

［5］Robinson W D，Kummerow C，Olson W S．A technique for enhancing and matching the resolution of microwave measurements from the SSM/I instrument［J］．Geoscience and Remote Sensing，IEEE Transactions on，1992，30（3）：419－429

［6］王永前，施建成，蔣靈梅．AMSR－E低頻亮溫數據空間分辨率提高以及不同波段亮溫數據組合應用時分辨率匹配的算法［J］．中國科學（地球科學），2011（2）：253－264 Wang Yongqian，Shi Jiancheng，Jiang Lingmei．The development of an algorithm to enhance and match the resolution of satellite measurements from AMSR－E［J］．Scientia Sinica（Terrae），2011（2）：253－264

［7］黃磊，周武，李延民．HY－2衛星掃描微波輻射計多通道分辨率匹配技術研究［J］．中國工程科學，2014（06）：65－69 Huang Lei，Zhou Wu，Li Yanmin．Study on channel resolution matching algorithm for HY－2satellite scanning microwave radiometer［J］．Engineering Sciences，2014（06）：65－69（in chinese）

［8］王振占．海面風場全極化微波輻射測量［D］．北京：中國科學院空間科學與應用研究中心，2005 Wang Zhenzhan．Sea surface wind vector measured by polarimetric microwave radiometer［D］．Beijing：National Space Science Center，CAS，2005（in Chinese）．

［9］楊虎，商建，呂利清．星載微波輻射計通道分辨率匹配技術及其在FY－3衛星MWRI中的應用［J］．上海航天，2012，29（1）：23－28 Yang Hu，Shang Jian，Lv Liqing．Study of channel resolution matching of spaceborne microwave radiometer and its application in MWRI of FY－3satellite［J］．Aerospace Shanghai 2012，29（1）：23－28（in Chinese）

［10］JAXA．AMSR－E level 1format description，NEB－00011E［R］．Tokyo，Japan：Aerospace Exploration Agency，2001

［11］Ashcroft P，Wentz F J．Algorithm theoretical basis document（ATBD）AMSR level 2Aalgorithm［R］．Santa Rosa：Remote Sensing Systems，2000

［12］Limaye A S，Crosson W L，Laymon C A．Estimating accuracy in optimal deconvolution of synthetic AMSRE observations［J］．Remote Sensing of Environment，2006，100（1）：133－142

［13］Migliaccio M，Gambardella A．Microwave radiometer spatial resolution enhancement［J］．IEEE Transactions on Geoscience and Remote Sensing，2005，43（5）：1159－1169

［14］Stutzman W L，Thiele G A．Antenna theory and design［M］．New York：John Wiley ＆Sons，2012

［15］任留成，呂泗洲，施全杰，等．空間地圖投影分類研究［J］．測繪學院學報，2002，19（3）：230－231 Ren Liucheng，Lv Sizhou，Shi Quanjie，et al．Research on the classification of space map projection［J］．Journal of Institute of Surveying and Mapping，2002，19（3）：230－231（in Chinese）．

［16］謝金華．遙感衛星軌道設計［D］．鄭州：中國人民解放軍信息工程大學2005 Xie Jinhua．Orbit design for remote sensing satellite［D］．Zhengzhou：The PLA Information Engineering University，2005（in Chinese）．

［17］何援軍．圖形變換的幾何化表示——論圖形變換和投影的若干問題之一［J］．計算機輔助設計與圖形學學報，2005，17（4）：723－728 He Yuanjun．Geometric representation of graphics transformation［J］．Journal of Computer Aided Design＆Computer Graphics，2005，17（4）：723－728（in Chinese）

［18］Farrar M R，Smith E A．Spatial resolution enhancement of terrestrial features using deconvolved SSM/I microwave brightness temperatures［J］．Geoscience and Remote Sensing，IEEE Transactions on，1992，30（2）：349－355

［19］國家衛星海洋應用中心．2014年中國海洋衛星應用報告［R］．北京：國家衛星海洋應用中心，2015 National Satellite Ocean Application Service．2014 China ocean satellite application report［R］．Beijing：NSOAS，2015（in Chinese）

（編輯：張小琳）

Smoothing Parameter Selection of Resolution Matching for Spaceborne Microwave Radiometer

WANG Zhaohui1，2LIAO Fei3，4SONG Qingtao1，2LIU Yuxin1，2
（1National Satellite Ocean Application Service，Beijing 100081，China）
（2Key Laboratory of Space Ocean Remote Sensing and Application，SOA，Beijing 100081，China）
（3Institute of Tropical and Marine Meteorology，CMA，Guangzhou 510080，China）
（4Guangzhou Meteorological Observatory，Guangzhou 511430，China）

In order to obtain accurate atmospheric and oceanographic parameters，it is required to resample and process the brightness temperature observed by spaceborne microwave radiometer in unified resolution．Based on satellite parameters and by using gradually cut circular aperture，the antenna patterns of spaceborne microwave radiometer are simulated in positive axis equidistant manner．In our Backus－Gilbert resampling experiments，we used the simulated antenna pattern with geographic information and real AMSR－E data to analyze the impact of smoothing parameter on the change of two key items，fit error and noise factor，and determined the optimal smoothing parameter that is the first non－negative smoothing parameter appearing in configured antenna pattern when the smoothing parameter changes from 0to infinity．The experiments indicate that the definite filter resampling technique which is often used currently can be used to get satisfactory results，high computational efficiency and application value．

ocean satellite；spaceborne microwave radiometer；AMSR－E；resolution matching；Backus－Gilbert algorithm

V443

A

10．3969/j．issn．1673－8748．2016．02．020

2016－01－08；

2016－02－25

國家自然科學基金面上項目（41276019，41076012）；海洋公益性行業科研專項（201305032）；廣東省科技計劃項目（2013B020200013）

王兆徽，男，碩士，主要從事微波遙感研究。Email：wzh@mail．nsoas．org．cn。